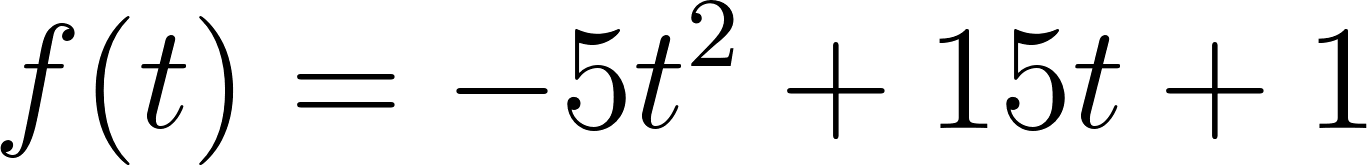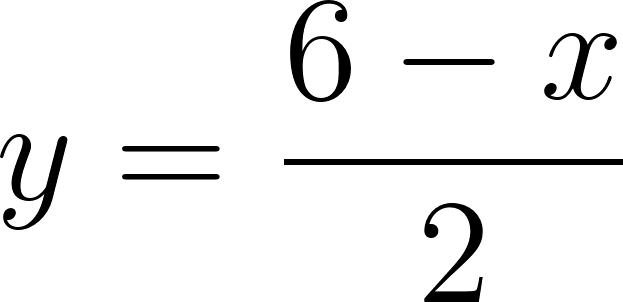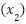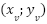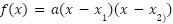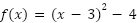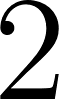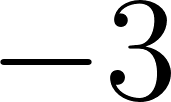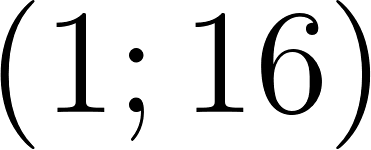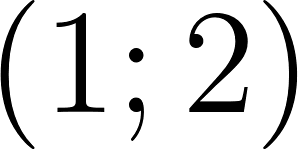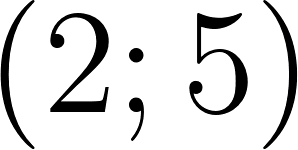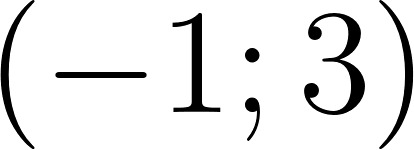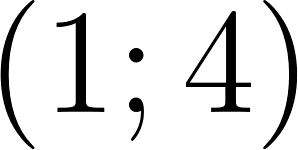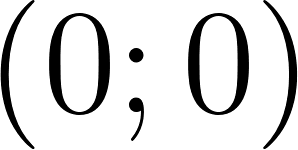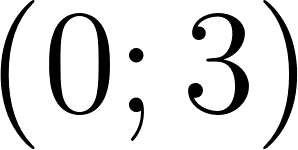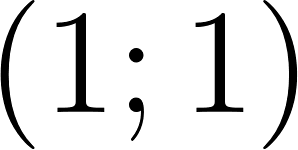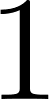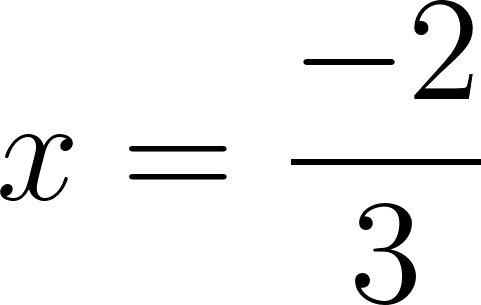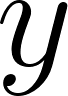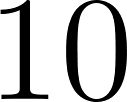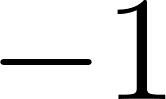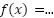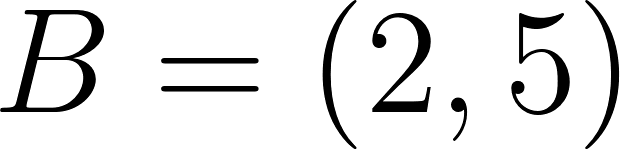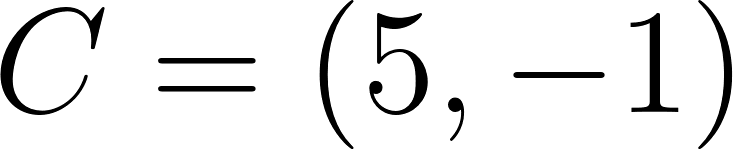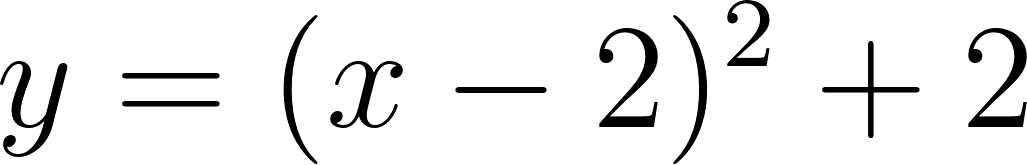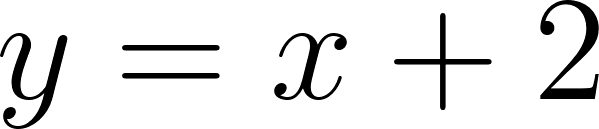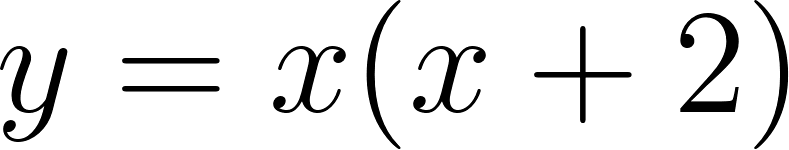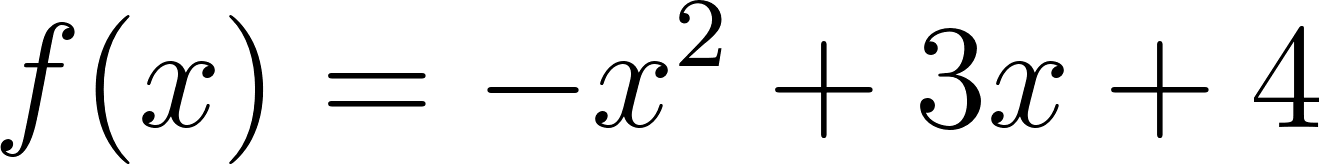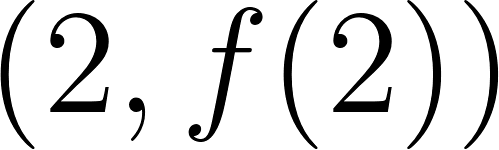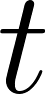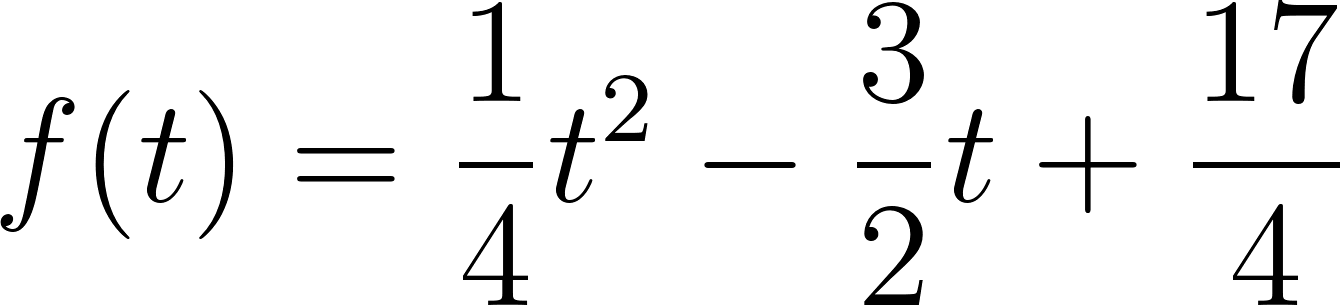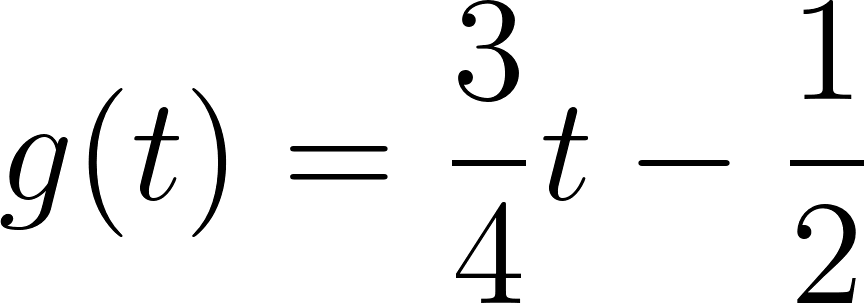Unidad 3
Modelos cuadráticos
Áreas, perímetros y movimientos
Objetivos de esta unidad:
|
Teoría
Transcripción del Prezi(2024):
Unidad 3:
Modelos cuadráticos
- Presentación de un problema.
- Resolución gráfica y análitica.
- ¡A trabajar!
- Resolver juntos.
- Algo más teórico.
- Practicar más.
- Distintas formas de expresión.
- Por tres puntos.
- Presentación de un problema:
- Problema: Parcela costeña. El propietario de un campo quiere plantar cierto tipo de lechuga en una parcela de forma rectangular lindera con un río. Para evitar destrozos de las vacas decide que debe cerrarlo con alambre tejido. Dispone de
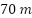 de alambre tejido, aprovechará que un lado del terreno da sobre el río y solamente pondrá alambrado en los otros lados.
de alambre tejido, aprovechará que un lado del terreno da sobre el río y solamente pondrá alambrado en los otros lados.
- Den una fórmula que exprese la superficie de la parcela en función de uno de los lados de la misma.
- Encuentren la longitud de los lados si la superficie cercada fuera de
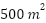 .
.
- Resolución gráfica y análitica:
- ¡A trabajar!:
Con lo visto en esta primera parte podrán resolver los Problemas 1 y 5 de la Unidad 3.
Problema 1:
En un terreno un granjero quiere delimitar una región rectangular con
un alambre de 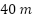 para hacer una zona de cultivos.
para hacer una zona de cultivos.
- Indiquen por lo menos cuatro posibles dimensiones (largo y ancho) de la zona de cultivo.
- ¿De qué dimensiones debería hacer el granjero la zona de cultivo si quiere maximizar su cosecha?
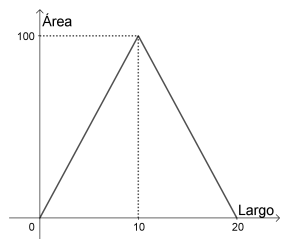
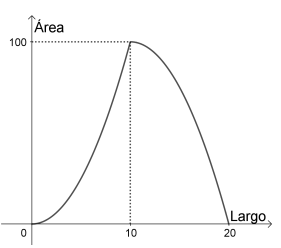
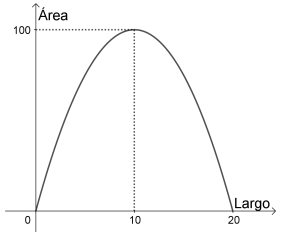
- Decidan, justificando adecuadamente, si alguno de los siguientes gráficos describe el área del rectángulo formado en función de la longitud de uno de los lados del rectángulo. Expliquen también las razones por las que descartan los gráficos que no corresponden. Si ninguno de los gráficos responde a lo pedido, propongan un gráfico que sí corresponde.
No es una Función Cuadrática | s(x) tiene a= -1, no 1 | s(x) tiene a= -1, no 1 |
C no es Cero | Correcto | x=40 no es raíz |
Resolución Problema 1:
Problema 5:
Un productor tiene una plantación de una hectárea con 40 naranjos; cada uno de ellos produce 500 naranjas por año. Se desea conocer cuál será la producción si se decide aumentar la cantidad de naranjos en esa parcela, sabiendo que por cada naranjo que se incorpora, la producción de cada uno disminuye en 5 unidades.
- Antes de hacer cálculos, expliquen con sus palabras por qué es esperable que la plantación se comporte aproximadamente de la manera que se describe.
- ¿Qué cantidad de naranjos adicionales anularían la producción?
- Construyan un gráfico a través del cuál se pueda describir y analizar la variación de la producción en función de los árboles adicionales plantados.
- ¿Qué número de árboles adicionales maximizará la producción? Expliquen y fundamenten su respuesta.
Resolución Problema 5:
Problema 5 Un productor tiene una plantación de una hectárea con 40 naranjos; cada uno de ellos produce 500 naranjas por año. Se desea conocer cuál será la producción si se decide aumentar la cantidad de naranjos en esa parcela, sabiendo que por cada naranjo que se incorpora, la producción de cada uno disminuye en 5 unidades.
- Antes de hacer cálculos, expliquen con sus palabras por qué es esperable que la plantación se comporte aproximadamente de la manera que se describe.
Los naranjos plantados disminuirán porque debe existir un máximo de naranjos que darán 500 naranjas cada uno anualmente y tal vez luego del naranjo 40 que tenemos como dato empezará a disminuir, es factible que sea el vértice de la función, y 20000 sea la cantidad óptima, ya que luego se disminuye por cada naranjo nuevo.
- ¿Qué cantidad de naranjos adicionales anularían la producción?
Para saber esto debemos proponer una función:
Sabemos que por cada nuevo naranjo se obtendrán 5 naranjas menos por cada plantación:

Que a los 40 naranjos le sumaremos más cantidad:
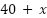
Con estos datos podemos presentar una función:

Sacamos factor común 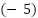 :
:
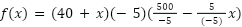 resolvemos
resolvemos
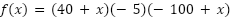
Quedándonos la forma factorizada, ordenamos:
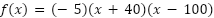
dónde identificamos el coeficiente principal, que dará la concavidad de la función, las raíces 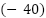 y
y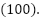
Teniendo en cuenta que las raíces nos dicen cuando la función se hace cero, podemos responder la consulta, con el naranjo 100 la producción se anularía, para confirmar esto, evaluamos la función para 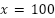 :
:
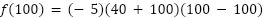
Como todo producto por cero es cero:

- Construyan un gráfico a través del cuál se pueda describir y analizar la variación de la producción en función de los árboles adicionales plantados.
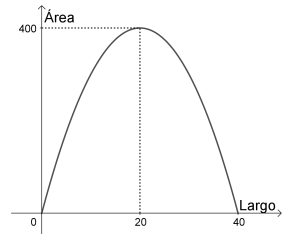
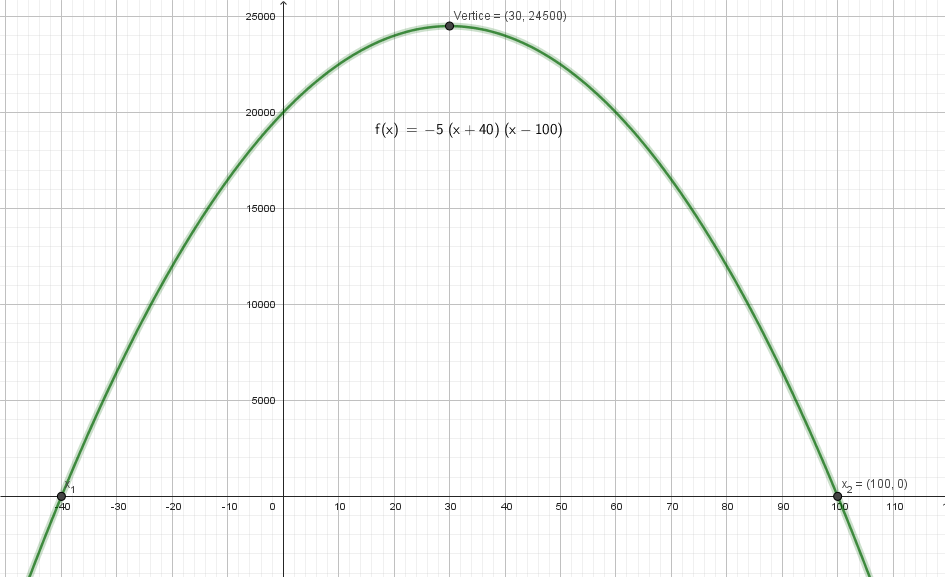
Gráfico:
Se puede observar que el vértice es 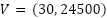 no el que se pensó antes de realizar los cálculos.
no el que se pensó antes de realizar los cálculos.
- ¿Qué número de árboles adicionales maximizará la producción? Expliquen y fundamenten su respuesta.
Por lo visto en el gráfico, el número de naranjos óptimos es 30, análiticamente podemos obtener la coordenaada 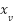 del vértice sacando el promedio de sus raíces ya que el vértice es simétrico respecto de la función:
del vértice sacando el promedio de sus raíces ya que el vértice es simétrico respecto de la función:
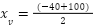
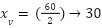
Para hallar la coordenada  del vértice evaluamos en la función:
del vértice evaluamos en la función:
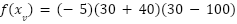

Comprobando que el 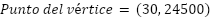
- Resolver juntos:
- Resuelvan el Problema 2, resolución en Función Cuadrática: Una introducción a partir de un problema.
Problema 2:
Una bolita de vidrio es lanzada hacia arriba desde 1 m de altura y con una velocidad de 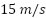 . Si la variable
. Si la variable 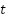 representa el tiempo (medido en segundos), la altura (en metros) a la que estará la bolita en cada instante viene dada por la fórmula:
representa el tiempo (medido en segundos), la altura (en metros) a la que estará la bolita en cada instante viene dada por la fórmula:
- ¿A qué altura del piso estará la bolita 0, 5 s después de ser lanzada?
- ¿A qué altura estará 2 s después de ser lanzada?
- ¿Se puede asegurar que la bolita estuvo ascendiendo durante los primeros dos segundos desde que fue lanzada?
- Observen que, para esta función, es
 . ¿Qué significa esta información en el contexto del problema?
. ¿Qué significa esta información en el contexto del problema? - Observen que
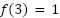 y
y 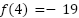 ¿Qué significan estos valores en el contexto del problema?
¿Qué significan estos valores en el contexto del problema? - ¿Cuánto tarda la bolita en llegar al piso?
Resolución Problema 2:
- Algo más teórico:
- Les proponemos resolver el Problema 3, deben anotar todas las conclusiones de este problema.
- Resolución en Video: Características de una Función Cuadrática.
Problema 3:
¿Qué ocurre con la gráfica de 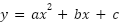 cuando:
cuando:
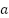 cambia mientras
cambia mientras 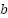 y
y 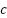 permanecen fijos.
permanecen fijos.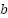 cambia mientras
cambia mientras 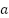 y
y 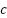 permanecen fijos,
permanecen fijos, 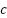 cambia mientras
cambia mientras 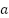 y
y 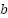 permanecen fijos.
permanecen fijos.
Resolución Problema 3:
- Practicar más:
- Hagamos un poco de práctica. Resuelvan los Problemas 6 al 14 en grupo.
Problema 6:
Una soguita que mide 30 cm está unida por sus extremos. Sosteniéndola con cuatro dedos se puede tensar para formar distintos rectángulos. Investiguen: ¿Hay un rectángulo que sea el de menor área de todos? ¿Hay alguno que tenga mayor área que todos los demás?.
Resolución Problema 6:
Problema 7:
Entre los pares de números positivos cuya suma es 30, encuentren aquellos dos cuyo producto es máximo.
Resolución Problema 7:
Problema 8:
Sobre la orilla recta de un canal se precisa delimitar un terreno rectangular alambrando los 3 lados que no pertenecen a la orilla. Hay que emplear 1800 metros de alambre tejido. ¿Cuáles deben ser las dimensiones del terreno para que tenga área máxima?.
Resolución Problema 8:
Problema 9:
- Accedan a este enlace https://www.geogebra.org/m/kzeu8kxr y observen cómo varía el cuadrilátero verde cuando se mueve el deslizador
 .
.
- Calculen el área del cuadrilátero para un par de valores de
 que elijan.
que elijan. - Determinar analíticamente para qué valor de
 es mínima el área del polígono verde.
es mínima el área del polígono verde.
- Lo mismo que en el ítem anterior, pero con la figura de este enlace: https://www.geogebra.org/m/zuxd56ne
Resolución Problema 9:
Problema 10:
Realicen en GeoGebra la siguiente construcción dinámica:
- La construcción debe moverse con un deslizador.
- Debe consistir en un rectángulo con una semicircunferencia sobre uno de sus lados, de manera que ese lado del rectángulo sea un diámetro de la circunferencia.
- Al mover el deslizador, el largo y el ancho del rectángulo deben variar, pero de tal manera que el perímetro total de la figura (formado por tres lados del rectángulo y por la semicircunferencia) mida siempre 8 unidades.
¿Para qué valor del deslizador el área de la figura resulta máxima?.
Resolución Problema 10:
Problema 11:
En un rectángulo de perímetro 100 se construye un cuadrilátero que tiene vértices en los puntos medios de los lados del rectángulo. ¿Cuáles deben ser las dimensiones del rectángulo para que el área del cuadrilátero sea máxima?.
Resolución Problema 11:
Problema 12:
Con 4 m de alambre queremos construir un círculo y un cuadrado. ¿Cuánto alambre hay que emplear en cada figura para lograr que la suma de las áreas de ellas sea la mínima posible? ¿Y si quisiéramos que la suma sea la máxima posible?
Resolución Problema 12:
Problema 13:
Un rectángulo está construido en la región limitada por los semiejes coordenados positivos y por la gráfica de la recta . ¿Qué longitud deben tener los lados del rectángulo para que su área sea máxima?.
Resolución Problema 13:
Problema 14:
Se deja caer una piedra desde el techo de un edificio que mide 80 m de altura y se quiere describir cómo varía la altura de la piedra en relación con el tiempo. La relación es la siguiente: 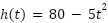 , con
, con 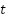 expresado en segundos y
expresado en segundos y  en metros.
en metros.
- ¿A qué altura se encuentra la piedra después de un segundo, y de dos y medio?
- ¿Cuántos segundos tarda la piedra en alcanzar una altura de 20 m?
- ¿En qué momento la piedra toca el suelo?
- Averigüen cuánto tarda la piedra en recorrer los primeros 20 m, y en los últimos 20 m antes de alcanzar el suelo.
- Averigüen cuántos metros recorre en los primeros 2 segundos, y en los últimos 2 segundos.
Resolución Problema 14:
- Distintas formas de expresión:
General o Polinómica (Se observa la ordenada al origen)
| Factorizada (Se observan las raíces)
| Canónica (Se observan las coordenadas del vértice)
|
|
|
|
|
|
|
- Con lo visto en este video pueden resolver los Problemas 16 al 21, 23, 24 al 28.
Problema 16:
Dadas las siguientes funciones definidas en el conjunto de los números reales:
- Hallen el máximo o el mínimo valor que puede alcanzar cada una y determinen en qué valor de
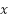 lo alcanza:
lo alcanza:
- Para cada una de las funciones anteriores, estudien si el gráfico de la función corta al eje
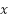 y en qué valores lo hace.
y en qué valores lo hace.
Resolución Problema 16:
Problema 17:
Hallen una expresión de una función cuadrática que verifique que sus raíces son y .
Resolución Problema 17:
Problema 18:
Hallen una expresión de una función cuadrática que verifique que sus raíces son y y que además pase por el punto .
Resolución Problema 18:
Problema 19:
Hallen una expresión de una función cuadrática que verifique que su vértice es el punto .
Resolución Problema 19:
Problema 20:
Hallen una expresión de una función cuadrática que verifique que su vértice es el punto y que además pase por el punto .
Resolución Problema 20:
Problema 21:
Hallen una expresión de una función cuadrática 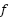 que verifique
que verifique 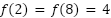 y que su coeficiente principal sea .
y que su coeficiente principal sea .
Resolución Problema 21:
Problema 23:
Obtengan la expresión de la función cuadrática, cuyo gráfico cumple las siguientes condiciones:
- Tiene vértice en el origen y pasa por .
- Pasa por los puntos de coordenadas , y .
- Vértice en y pasa por .
- Tiene raíces
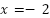 y
y 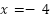 , y el coeficiente del término cuadrático es .
, y el coeficiente del término cuadrático es .
Resolución Problema 23:
Problema 24:
Sabiendo que el eje de simetría de la función cuadrática 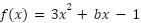 es la recta de ecuación obtengan las coordenadas de los puntos de intersección de la función cuadrática con la recta
es la recta de ecuación obtengan las coordenadas de los puntos de intersección de la función cuadrática con la recta  .
.
Resolución Problema 24:
Problema 25:
Completen:
La función cuadrática cuyo gráfico corta al eje de ordenadas (eje ) en y tiene raíces y tiene expresión en forma canónica, |
Resolución Problema 25:
Problema 26:
- Hallen la expresión de una función cuadrática que verifique las siguientes condiciones:
- Su eje de simetría sea
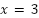 .
. - Su gráfico corte al eje en .
- Su gráfico corte al eje en .
- Grafiquen la función, indicando las raíces y el vértice.
Resolución Problema 26:
Problema 27:
Sea 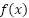 la función cuadrática cuyo gráfico tiene vértice en y verifica
la función cuadrática cuyo gráfico tiene vértice en y verifica 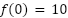 .
.
- Hallar la fórmula que la define.
- Hallar las raíces y realizar un gráfico aproximado de la función.
Resolución Problema 27:
Problema 28:
La ecuación de una misma función cuadrática se puede escribir de muchas formas equivalentes. Decidan si las siguientes expresiones corresponden o no a una misma función.
Resolución Problema 28:
- Por tres puntos:
- Video: Ecuación de una Función Cuadrática.
- Resolver Problemas 15 y 22.
Problema 15:
Encuentren en cada caso, si es posible, la fórmula de una función cuadrática cuyo gráfico pasa por los puntos dados.
- ; ; .
- ; .
- ; ; .
Resolución Problema 15:
Problema 22:
Hallen la función cuadrática que verifica 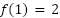 ,
, 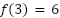 y
y 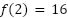 .
.
Resolución Problema 22:
Práctica
Problema 1(): En un terreno un granjero quiere delimitar una región rectangular con un alambre de 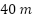 para hacer una zona de cultivos.
para hacer una zona de cultivos.
- Indiquen por lo menos cuatro posibles dimensiones (largo y ancho) de la zona de cultivo.
- ¿De qué dimensiones debería hacer el granjero la zona de cultivo si quiere maximizar su cosecha?
- Decidan, justificando adecuadamente, si alguno de los siguientes gráficos describe el área del rectángulo formado en función de la longitud de uno de los lados del rectángulo. Expliquen también las razones por las que descartan los gráficos que no corresponden. Si ninguno de los gráficos responde a lo pedido, propongan un gráfico que sí corresponde.
No es una Función Cuadrática | s(x) tiene a= -1, no 1 | s(x) tiene a= -1, no 1 |
C no es Cero | Correcto | x=40 no es raíz |
Problema 2: Una bolita de vidrio es lanzada hacia arriba desde 1 m de altura y con una velocidad de 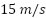 . Si la variable
. Si la variable 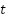 representa el tiempo (medido en segundos), la altura (en metros) a la que estará la bolita en cada instante viene dada por la fórmula:
representa el tiempo (medido en segundos), la altura (en metros) a la que estará la bolita en cada instante viene dada por la fórmula:
- ¿A qué altura del piso estará la bolita 0, 5 s después de ser lanzada?
- ¿A qué altura estará 2 s después de ser lanzada?.
- ¿Se puede asegurar que la bolita estuvo ascendiendo durante los primeros dos segundos desde que fue lanzada?.
- Observen que, para esta función, es
 . ¿Qué significa esta información en el contexto del problema?.
. ¿Qué significa esta información en el contexto del problema?. - Observen que
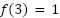 y
y 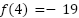 ¿Qué significan estos valores en el contexto del problema?.
¿Qué significan estos valores en el contexto del problema?. - ¿Cuánto tarda la bolita en llegar al piso?
Problema 3() ¿Qué ocurre con la gráfica de 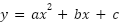 cuando:
cuando:
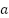 cambia mientras
cambia mientras 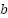 y
y 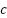 permanecen fijos.
permanecen fijos.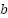 cambia mientras
cambia mientras 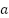 y
y 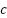 permanecen fijos.
permanecen fijos.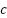 cambia mientras
cambia mientras 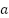 y
y 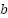 permanecen fijos.
permanecen fijos.
Problema 4:
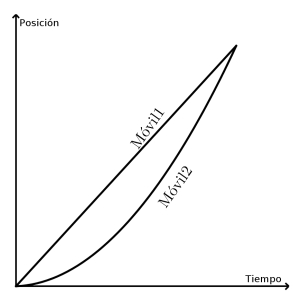
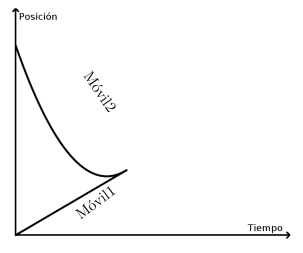
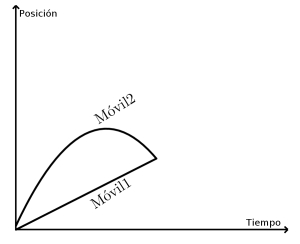
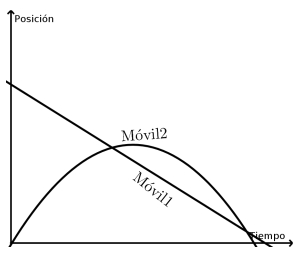
- Decidan a cuál de los siguientes gráficos puede corresponder la descripción del recuadro.
El Móvil 1 y el Móvil 2 partieron al mismo tiempo, pero desde distintas posiciones, viajando uno hacia el otro. El Móvil 1 llevaba velocidad constante, pero el Móvil 2 iba frenando. Finalmente, el Móvil 2 se detuvo y comenzó a regresar sobre sus pasos. Apenas después de comenzar el regreso, el Móvil 1 lo alcanzó. |
- Para cada uno de los otros tres gráficos, escriban una descripción similar que se ajuste a lo que nos muestran.
Problema 5 Un productor tiene una plantación de una hectárea con 40 naranjos; cada uno de ellos produce 500 naranjas por año. Se desea conocer cuál será la producción si se decide aumentar la cantidad de naranjos en esa parcela, sabiendo que por cada naranjo que se incorpora, la producción de cada uno disminuye en 5 unidades.
- Antes de hacer cálculos, expliquen con sus palabras por qué es esperable que la plantación se comporte aproximadamente de la manera que se describe.
- ¿Qué cantidad de naranjos adicionales anularían la producción?
- Construyan un gráfico a través del cuál se pueda describir y analizar la variación de la producción en función de los árboles adicionales plantados.
- ¿Qué número de árboles adicionales maximizará la producción?. Expliquen y fundamenten su respuesta
Problema 6() Una soguita que mide 30 cm está unida por sus extremos. Sosteniéndola con cuatro dedos se puede tensar para formar distintos rectángulos. Investiguen: ¿Hay un rectángulo que sea el de menor área de todos? ¿Hay alguno que tenga mayor área que todos los demás?.
Problema 7: Entre los pares de números positivos cuya suma es 30, encuentren aquellos dos cuyo producto es máximo.
Problema 8: Sobre la orilla recta de un canal se precisa delimitar un terreno rectangular alambrando los 3 lados que no pertenecen a la orilla. Hay que emplear 1800 metros de alambre tejido. ¿Cuáles deben ser las dimensiones del terreno para que tenga área máxima?.
Problema 9:
- Accedan a este enlace https://www.geogebra.org/m/kzeu8kxr y observen cómo varía el cuadrilátero verde cuando se mueve el deslizador
 .
.
- Calculen el área del cuadrilátero para un par de valores de
 que elijan.
que elijan. - Determinen analíticamente para qué valor de
 es mínima el área del polígono verde.
es mínima el área del polígono verde.
- Lo mismo que en el ítem anterior, pero con la figura de este enlace: https://www.geogebra.org/m/zuxd56ne
Problema 10() Realicen en GeoGebra la siguiente construcción dinámica:
- La construcción debe moverse con un deslizador.
- Debe consistir en un rectángulo con una semicircunferencia sobre uno de sus lados, de manera que ese lado del rectángulo sea un diámetro de la circunferencia.
- Al mover el deslizador, el largo y el ancho del rectángulo deben variar, pero de tal manera que el perímetro total de la figura (formado por tres lados del rectángulo y por la semicircunferencia) mida siempre 8 unidades.
¿Para qué valor del deslizador el área de la figura resulta máxima?.
Problema 11 En un rectángulo de perímetro 100 se construye un cuadrilátero que tiene vértices en los puntos medios de los lados del rectángulo. ¿Cuáles deben ser las dimensiones del rectángulo para que el área del cuadrilátero sea máxima?.
Problema 12 Con 4 m de alambre queremos construir un círculo y un cuadrado. ¿Cuánto alambre hay que emplear en cada figura para lograr que la suma de las áreas de ellas sea la mínima posible? ¿Y si quisiéramos que la suma sea la máxima posible?.
Problema 13 Un rectángulo está construido en la región limitada por los semiejes coordenados positivos y por la gráfica de la recta . ¿Qué longitud deben tener los lados del rectángulo para que su área sea máxima?.
Problema 14: Se deja caer una piedra desde el techo de un edificio que mide 80 m de altura y se quiere describir cómo varía la altura de la piedra en relación con el tiempo. La relación es la siguiente 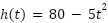 , con
, con 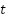 expresado en segundos y
expresado en segundos y  en metros.
en metros.
- ¿A qué altura se encuentra la piedra después de un segundo, y de dos y medio?.
- ¿Cuántos segundos tarda la piedra en alcanzar una altura de 20 m?.
- ¿En qué momento la piedra toca el suelo?.
- Averigüen cuánto tarda la piedra en recorrer los primeros 20 m, y en los últimos 20 m antes de alcanzar el suelo.
- Averigüen cuántos metros recorre en los primeros 2 segundos, y en los últimos 2 segundos.
Problema 15 Encuentren en cada caso, si es posible, la fórmula de una función cuadrática cuyo gráfico pasa por los puntos dados.
- ; ; .
- ; .
- ; ; .
Problema 16 Dadas las siguientes funciones definidas en el conjunto de los números reales:
- Hallen el máximo o el mínimo valor que puede alcanzar cada una y determinen en qué valor de
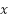 lo alcanza:
lo alcanza:
- Para cada una de las funciones anteriores, estudien si el gráfico de la función corta al eje
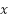 y en qué valores lo hace.
y en qué valores lo hace.
Problema 17 Hallen una expresión de una función cuadrática que verifique que sus raíces son y .
Problema 18 Hallen una expresión de una función cuadrática que verifique que sus raíces son y y que además pase por el punto .
Problema 19 Hallen una expresión de una función cuadrática que verifique que su vértice es el punto .
Problema 20 Hallen una expresión de una función cuadrática que verifique que su vértice es el punto y que además pase por el punto .
Problema 21 Hallen una expresión de una función cuadrática 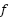 que verifique
que verifique 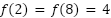 y que su coeficiente principal sea .
y que su coeficiente principal sea .
Problema 22 Hallen la función cuadrática que verifica 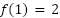 ,
, 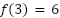 y
y 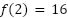 .
.
Problema 23 Obtengan la expresión de la función cuadrática, cuyo gráfico cumple las siguientes condiciones:
- Tiene vértice en el origen y pasa por .
- Pasa por los puntos de coordenadas , y .
- Vértice en y pasa por .
- Tiene raíces
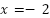 y
y 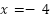 , y el coeficiente del término cuadrático es .
, y el coeficiente del término cuadrático es .
Problema 24 Sabiendo que el eje de simetría de la función cuadrática 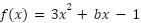 es la recta de ecuación obtengan las coordenadas de los puntos de intersección de la función cuadrática con la recta
es la recta de ecuación obtengan las coordenadas de los puntos de intersección de la función cuadrática con la recta  .
.
Problema 25 Completen:
La función cuadrática cuyo gráfico corta al eje de ordenadas (eje ) en y tiene raíces y tiene expresión en forma canónica, |
Problema 26
- Hallen la expresión de una función cuadrática que verifique las siguientes condiciones:
- Su eje de simetría sea
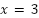 .
. - Su gráfico corte al eje en .
- Su gráfico corte al eje en .
- Grafiquen la función, indicando las raíces y el vértice.
Problema 27 Sea 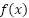 la función cuadrática cuyo gráfico tiene vértice en y verifica
la función cuadrática cuyo gráfico tiene vértice en y verifica 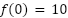 .
.
- Hallar la fórmula que la define.
- Hallar las raíces y realizar un gráfico aproximado de la función.
Problema 28 La ecuación de una misma función cuadrática se puede escribir de muchas formas equivalentes. Decidan si las siguientes expresiones corresponden o no a una misma función.
Problema 29 Hallen, si existen, las coordenadas de los puntos de intersección de las parábolas determinadas por y la recta dada por . Representen gráficamente.
Problema 30 Hallen, si existen las coordenadas de los puntos de intersección de las parábolas determinadas por y . Representen gráficamente.
Problema 31 Consideren la función cuadrática dada por .
- Encuentren la ecuación de una recta que intersecta al gráfico de en el punto .
- Encuentren la ecuación de una recta que intersecta al gráfico de solamente en el punto .
- ¿Son equivalentes los dos ítems anteriores?. Expliquen por qué, ilustrando la explicación con los gráficos correspondientes.
Problema 32 Dos móviles se desplazan de manera que para cada instante de tiempo sus posiciones vienen dadas por:
Móvil 1:
Móvil 2:
- Se sabe que el Móvil 1 partió en el instante 0 y que el Móvil 2 partió desde la posición 0. ¿Quién partió antes?.
- ¿En qué instantes y en qué posiciones se cruzaron?.
- Cuando se cruzaron, ¿estaban viajando uno hacía el otro o iban los dos en el mismo sentido?.
Extra 2023:
2. En la clase del 12/05 trabajamos con un problema que terminó modelizada como una función cuadrática:
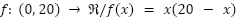
- Grafiquen la función.
- Encuentren las medidas de los lados de todos los rectángulos que se pueden formar con ese alambre de
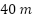 , de manera que el área sea
, de manera que el área sea 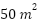 .
.
- ¿Cómo se modifican la función y el gráfico si en vez de
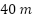 de alambre se dispone de
de alambre se dispone de  de alambre?
de alambre?
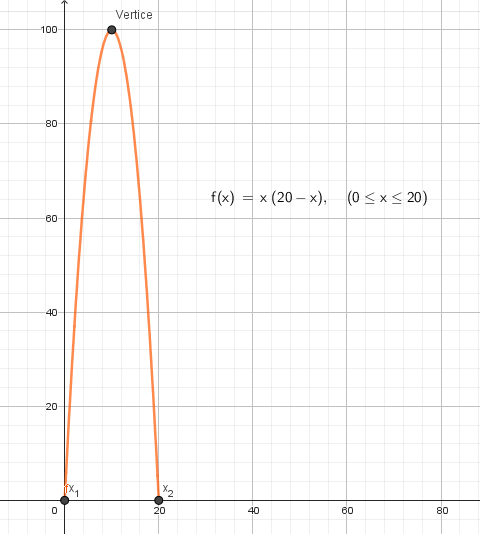
- En la clase del 12/05 trabajamos con un problema que terminó modelizándose con una función cuadrática:
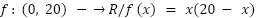
- Grafiquen la función.
Gráfico:
:
- Encuentren las medidas de los lados de todos los rectángulos que se pueden formar con ese alambre de 40 m, de manera que el área sea
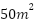 .
.
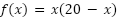 siendo el área
siendo el área 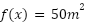
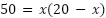 realizamos la propiedad distributiva
realizamos la propiedad distributiva
 igualamos a cero
igualamos a cero
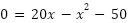
Aplicamos la resolvente(Bhaskara en el vídeo teórico) identificando como 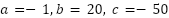
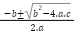
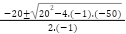
 y
y 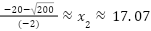
Las raíces son las medidas de los lados que nos darán como resultado una área de 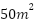 .
.
- ¿Cómo se modifican la función y el gráfico si en vez de 40 m de alambre se dispone de 100 m de alambre?
Si el perímetro es:  despejamos
despejamos
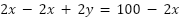
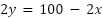
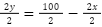
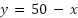
Siendo el 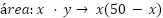 la función nos queda:
la función nos queda:
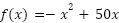
Y el gráfico:
Se aprecia el cambio de las raíces y su vértice, así como también que abarca superficies superiores con respecto al alambrado anterior.
Para ir pensando porque tendremos que aprenderlo
Al igual que pasa con las funciones lineales, hay cálculos y manejos que tenemos que saber hacer, respecto de la función cuadrática. A continuación va una lista de problemas formulados en forma abstracta, fuera de los contextos de alambrados y plantaciones con los que trabajamos en clase.
Léelos con atención, identificá cuàles no sabrías ni cómo empezar y asistí a las consultas del martes 16 para trabajar con ellos.
- Dados tres puntos no alineados y con distintas abscisas, escribir una fórmula de la función cuadrática que pasa por ellos.
- Dados dos puntos, escribir la fórmula de todas las funciones cuadráticas que pasan por ellos.
- La fórmula de una función cuadrática se puede escribir como:
- Polinómica:

- Canónica:

- Factorizada:
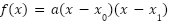
Siempre con 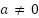
Dada una función cuadrática expresada de cualquiera de las formas (a) Polinómica, (b) Canónica o (c) Factorizada, manipular la expresión algebraica para expresarla de cualquiera de las otras dos formas.
- . Dada una función cuadrática en cualquiera de las formas (a) Polinómica, (b) Canónica o (c) Factorizada y un punto
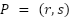 decidir si el punto pertenece o no al gráfico de la función.
decidir si el punto pertenece o no al gráfico de la función. - Resolver ecuaciones de las formas:
- Polinómica:

- Canónica:
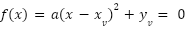
- Factorizada:
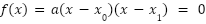
- Dada una función cuadrática en cualquiera de las formas (a) Polinómica, (b) Canónica o (c) Factorizada construir la parábola, que es su gráfico.
- Dada una función cuadrática en cualquiera de las formas (a) Polinómica, (b) Canónica o (c) Factorizada identificar el eje de simetría de la parábola (que es su gráfico).
- Dada una función cuadrática en cualquiera de las formas (a) Polinómica, (b) Canónica o (c) Factorizada identificar el vértice de la parábola (que es su gráfico).
- Dada una función cuadrática en cualquiera de las formas (a) Polinómica, (b) Canónica o (c) Factorizada encontrar pares de puntos
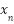 ,
, 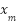 , tales que
, tales que  .
.
- Dadas dos funciones cuadráticas determinar la intersección de sus gráficas y decidir si se trata de un punto, de dos puntos o de ningún punto.
- Dadas una función cuadrática y una lineal determinar la intersección de sus gráficas y decidir si se trata de un punto, de dos puntos o de ningún punto.