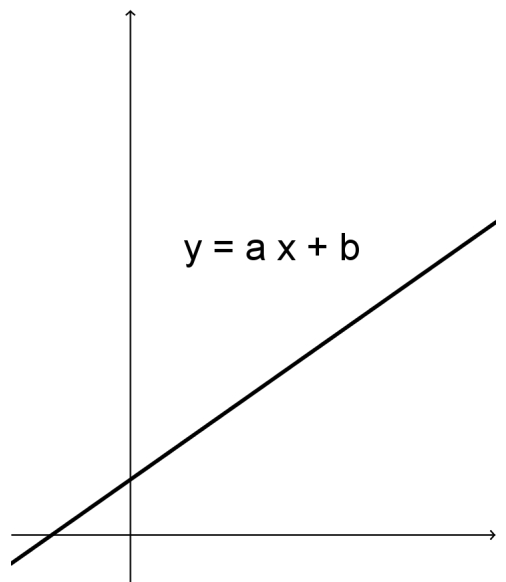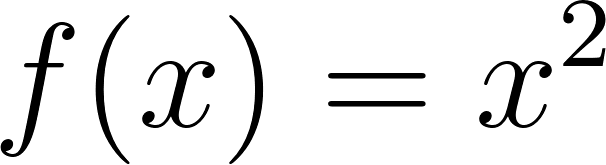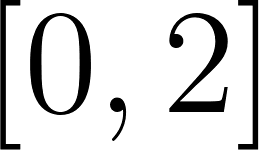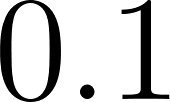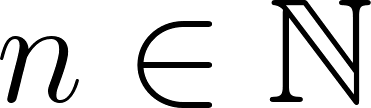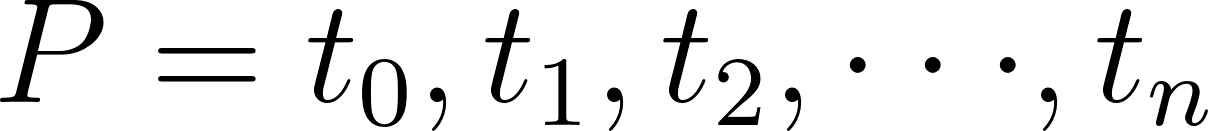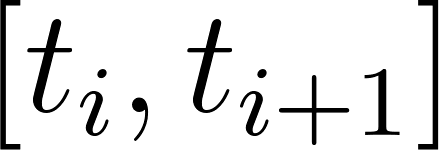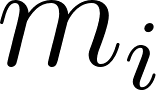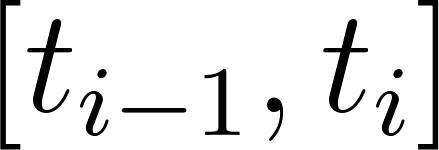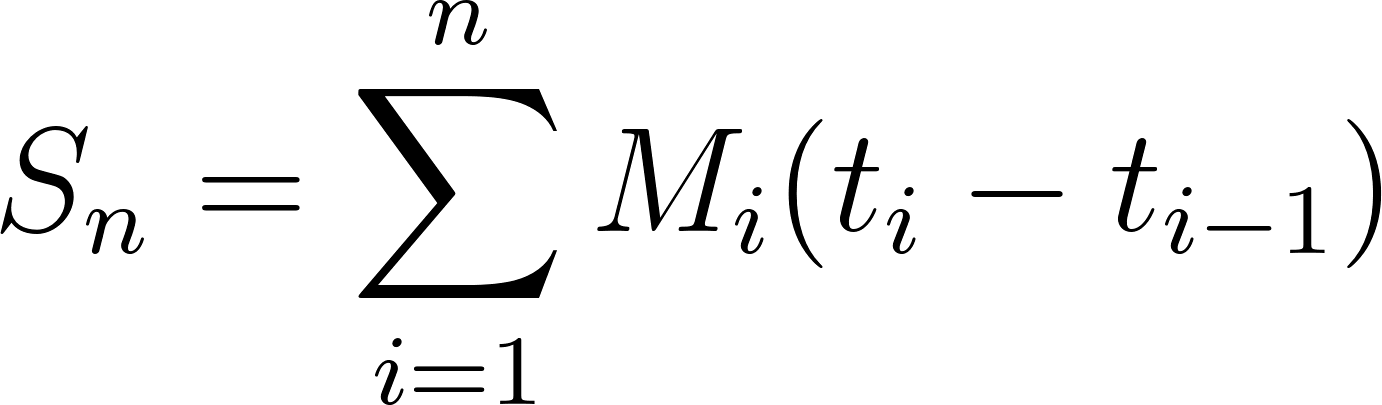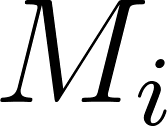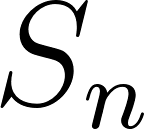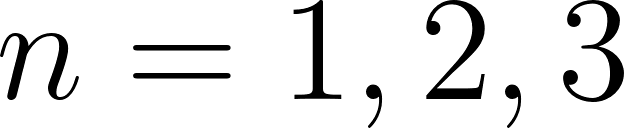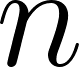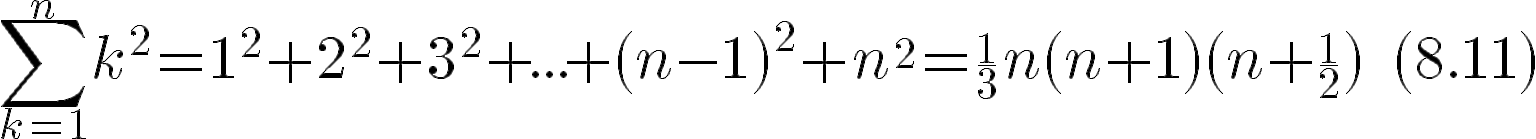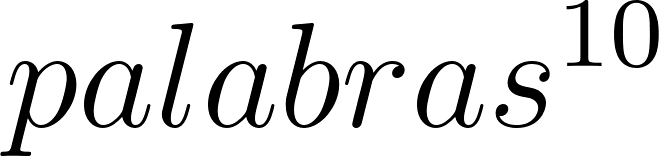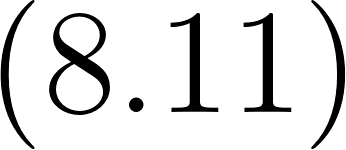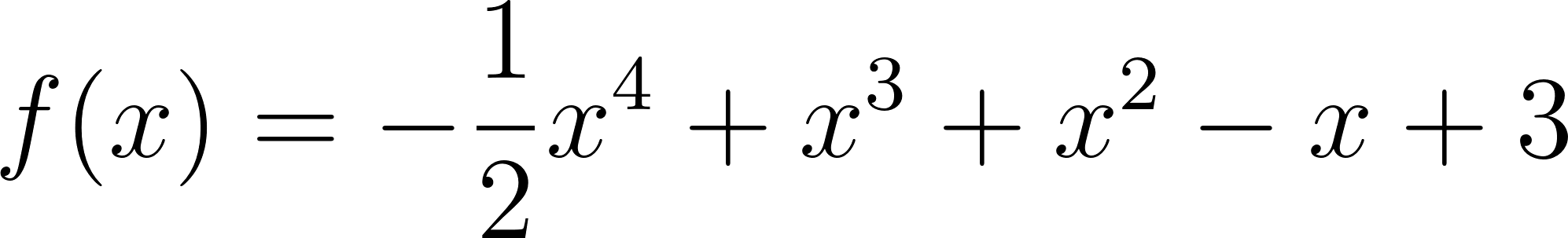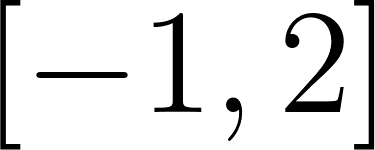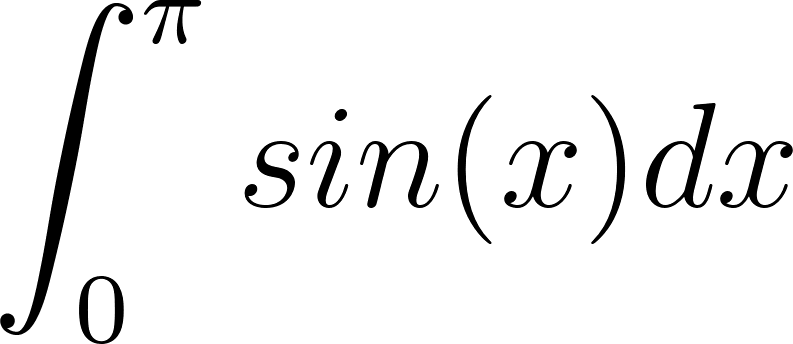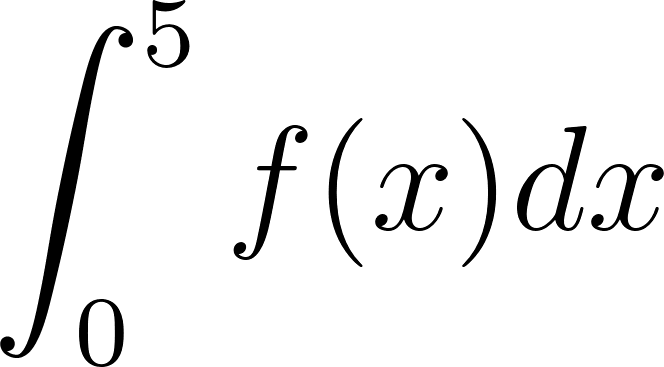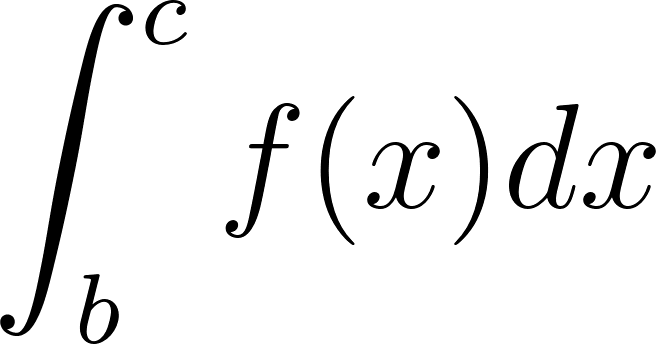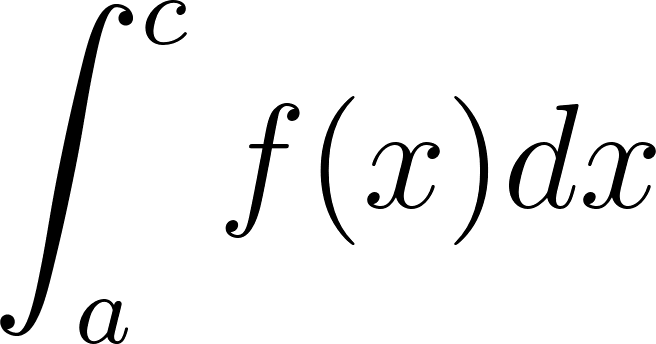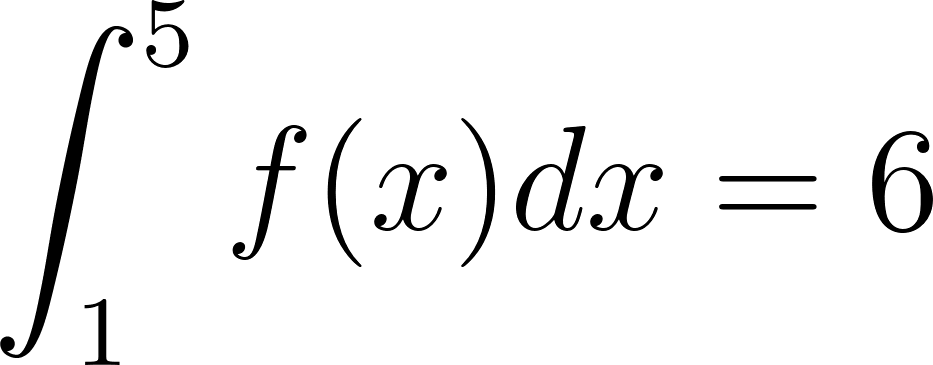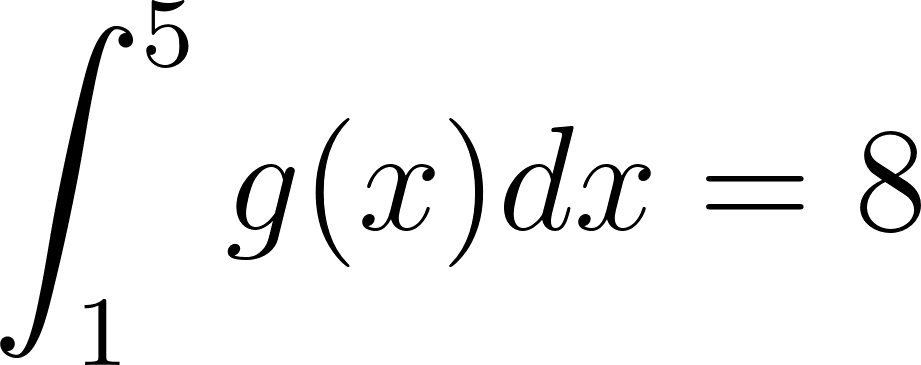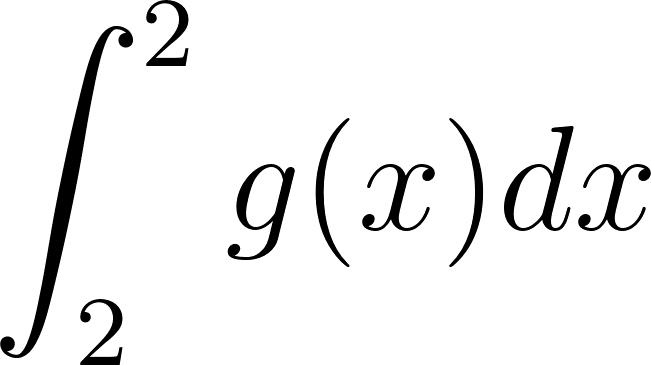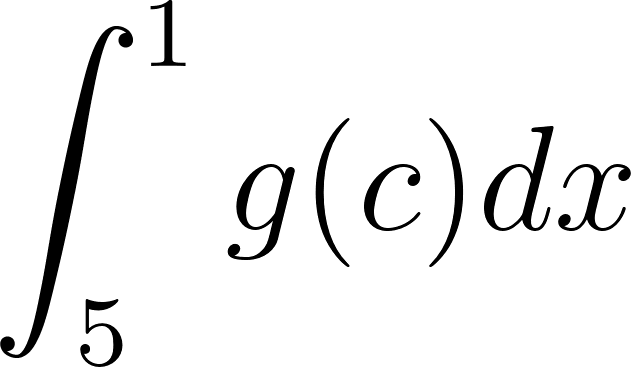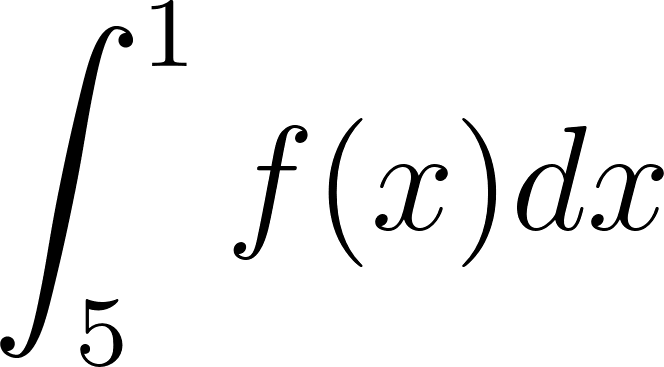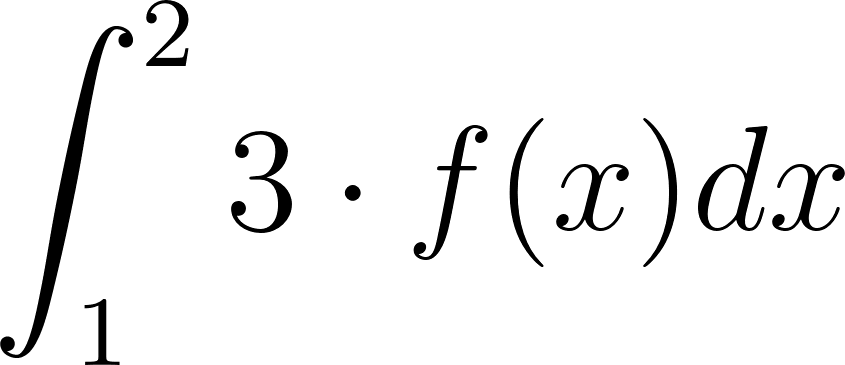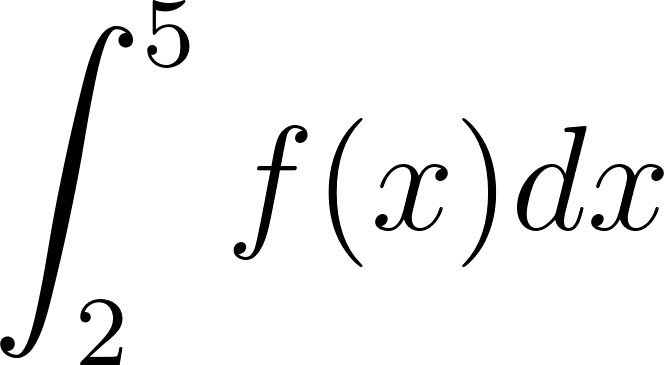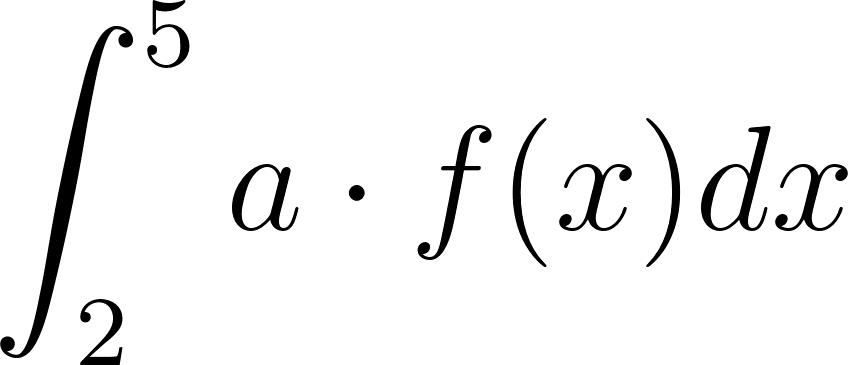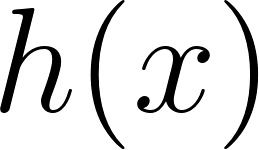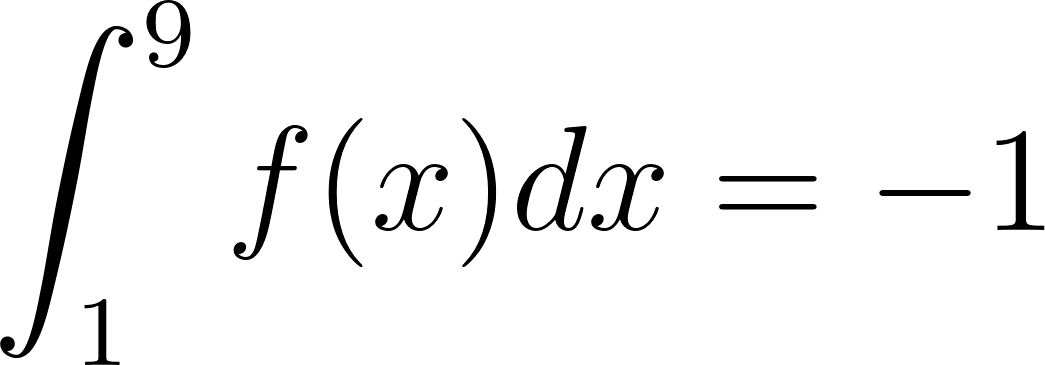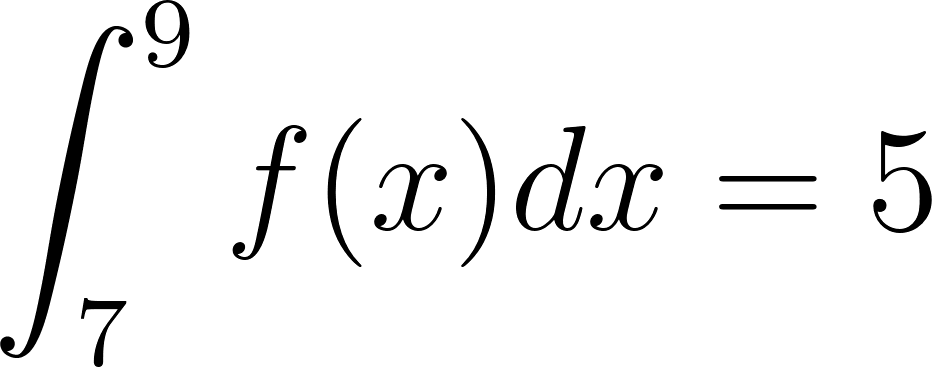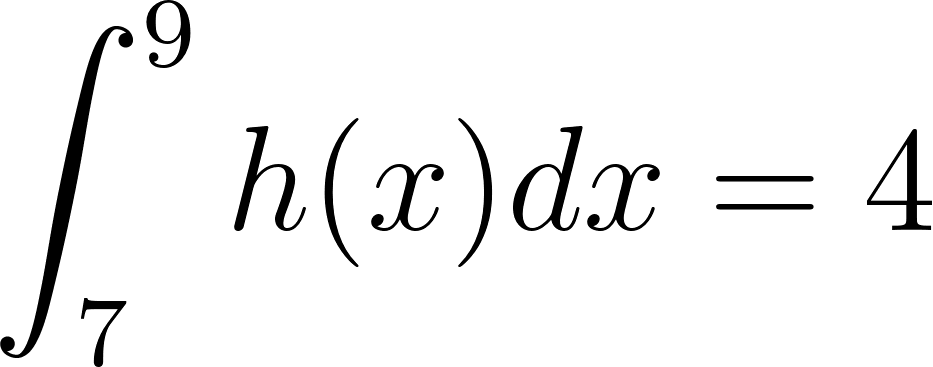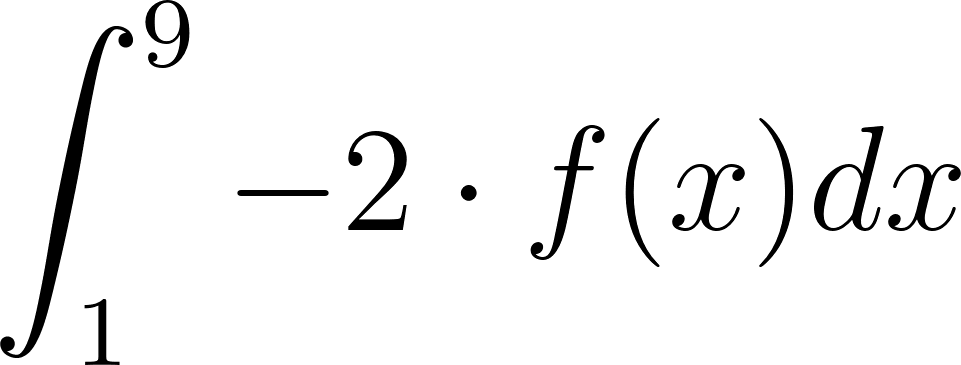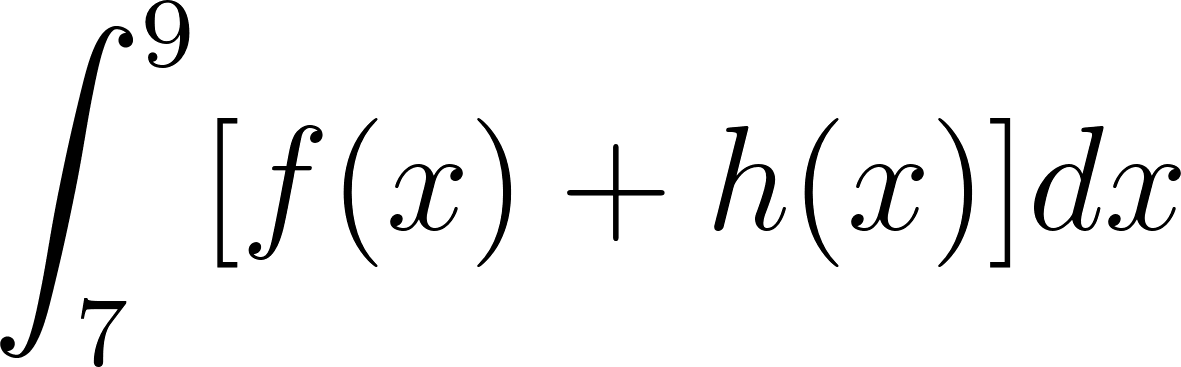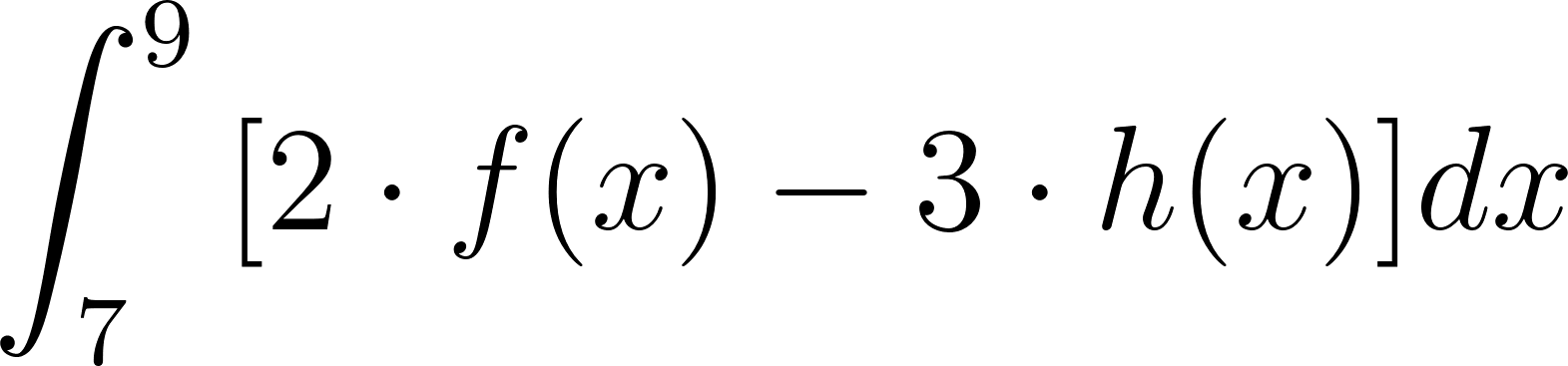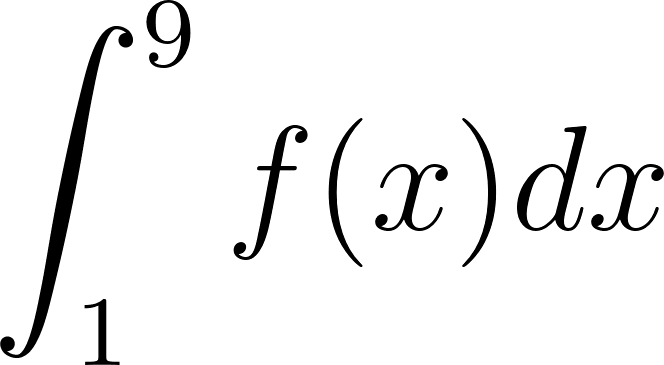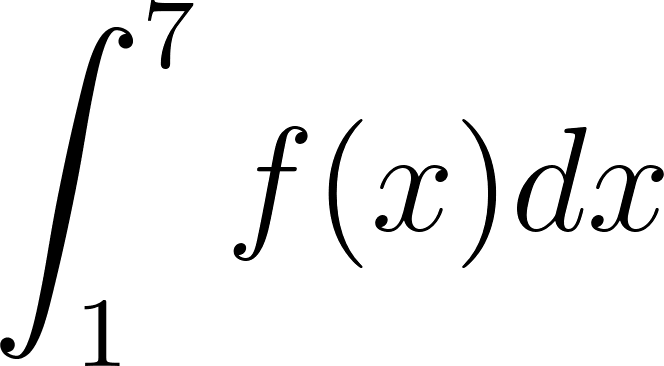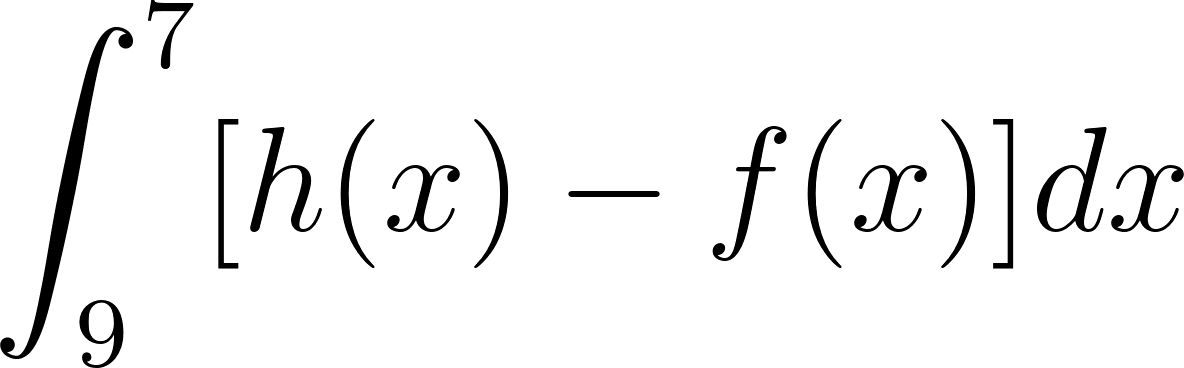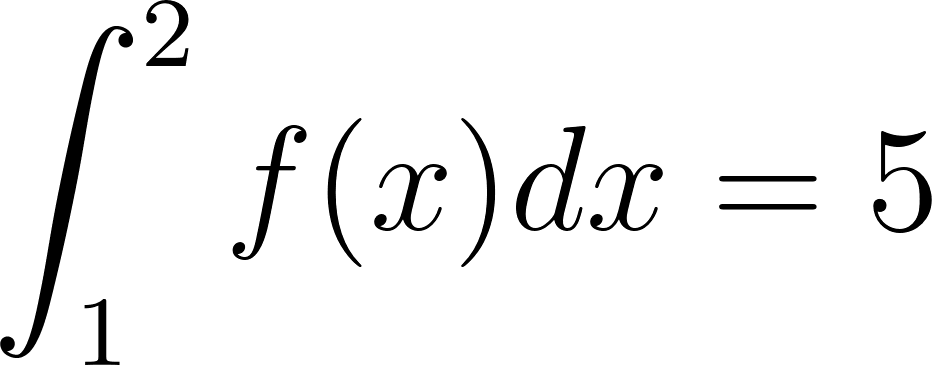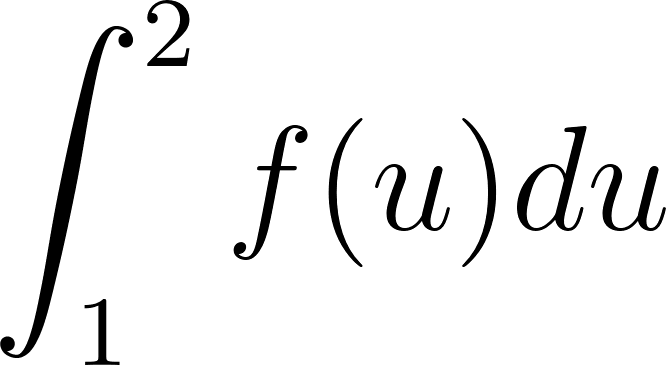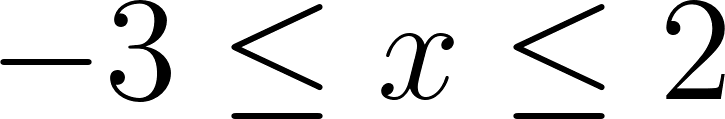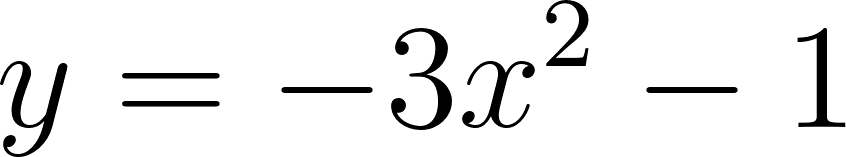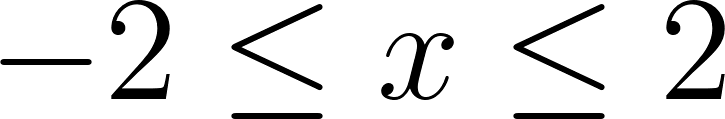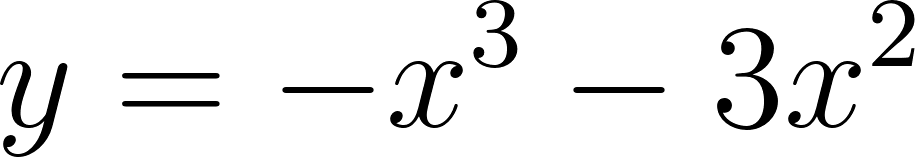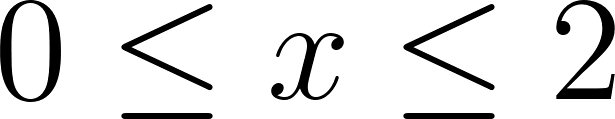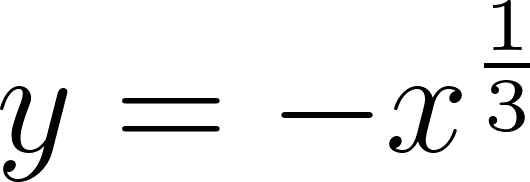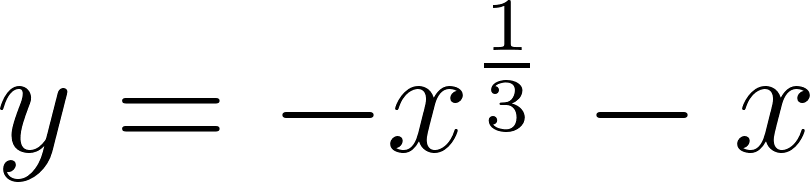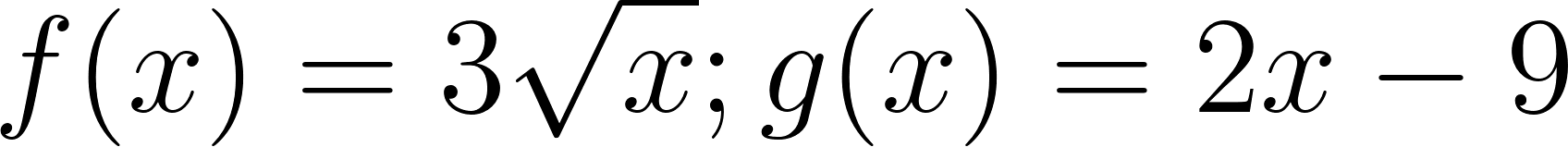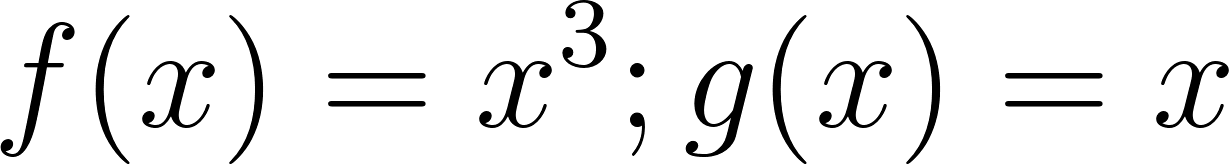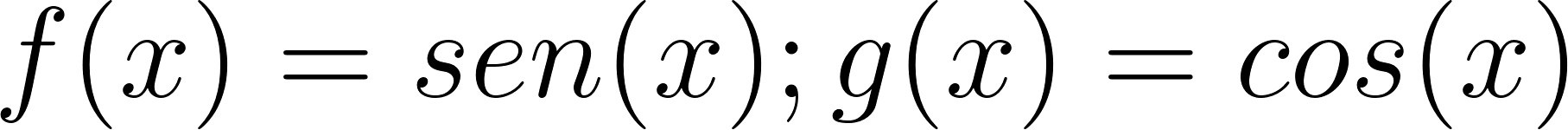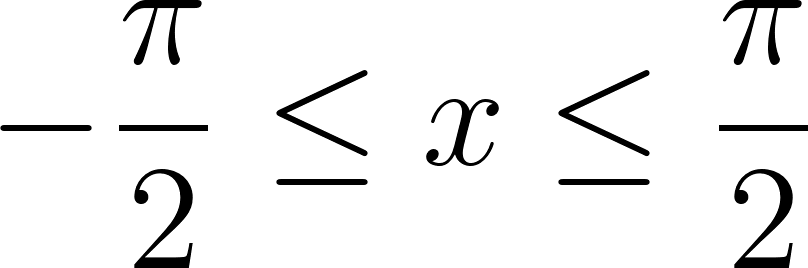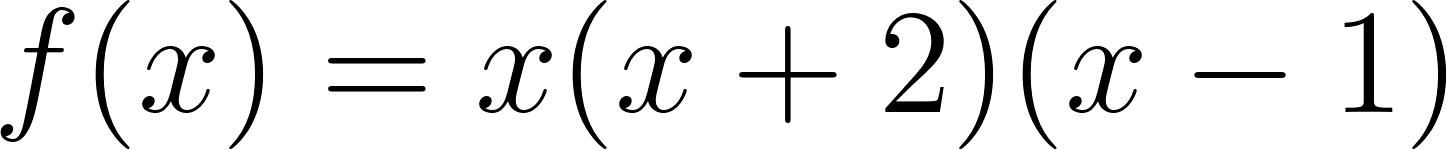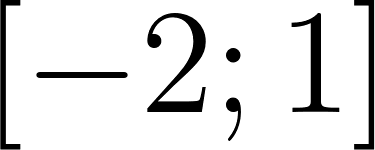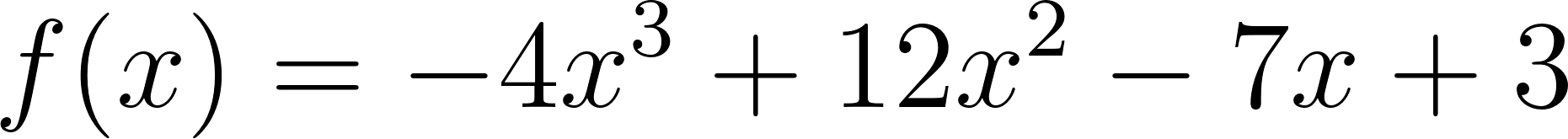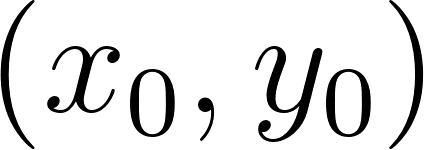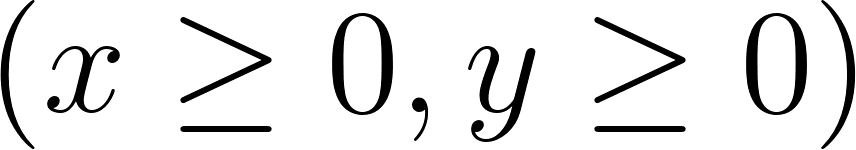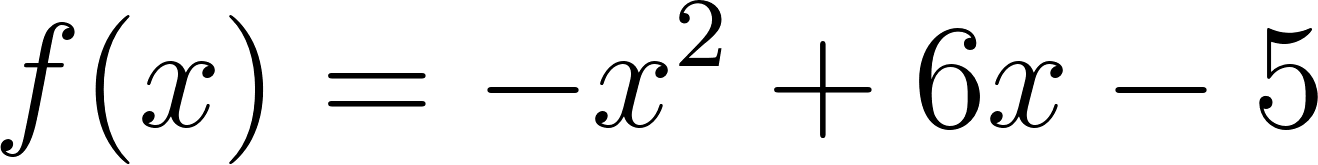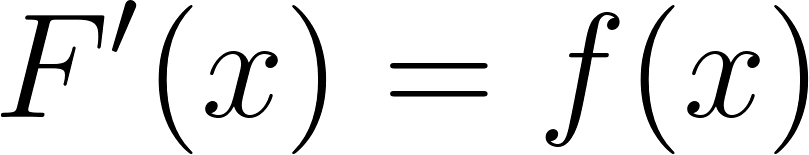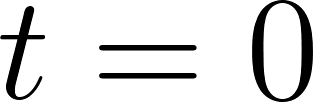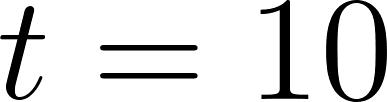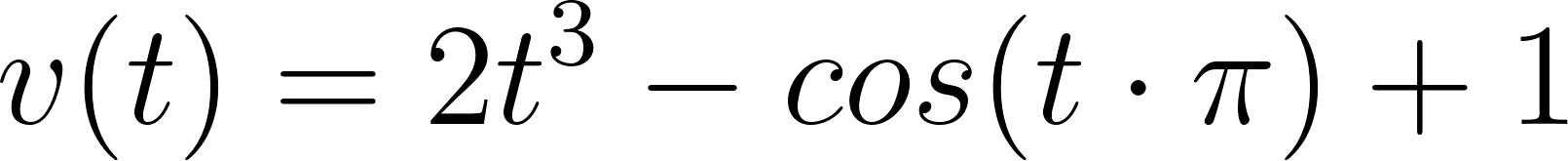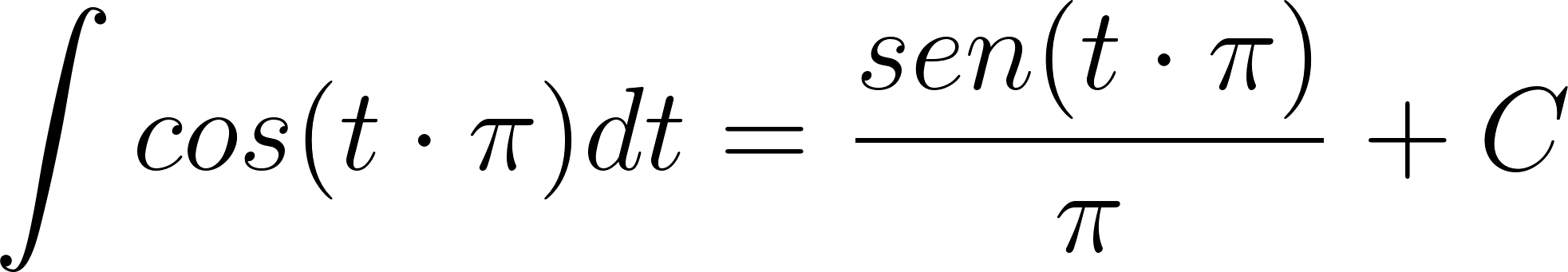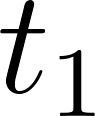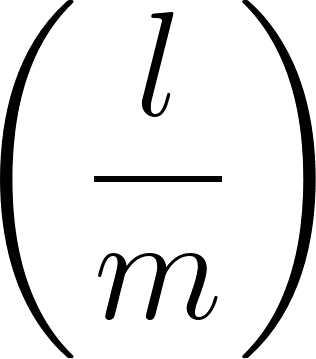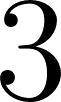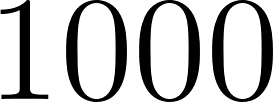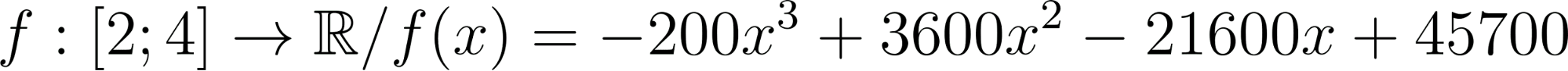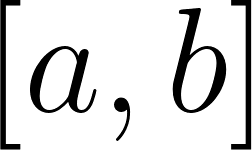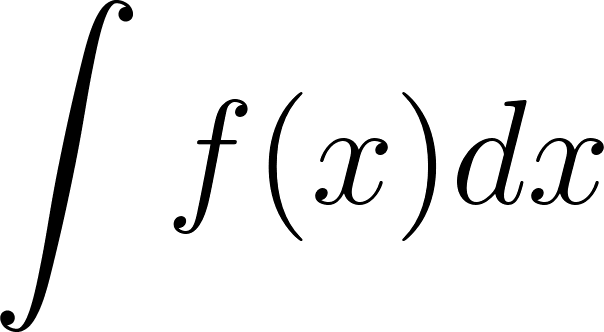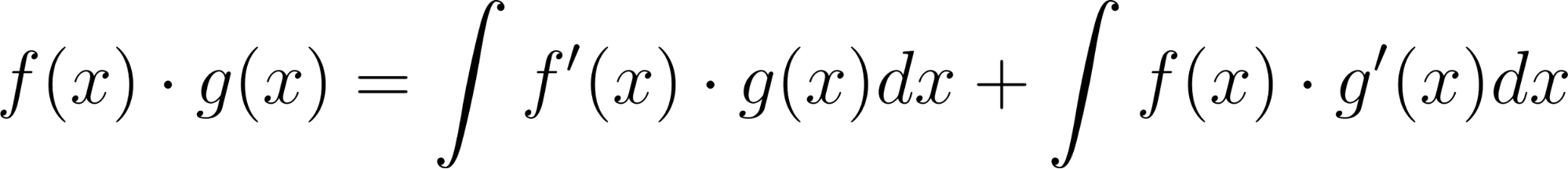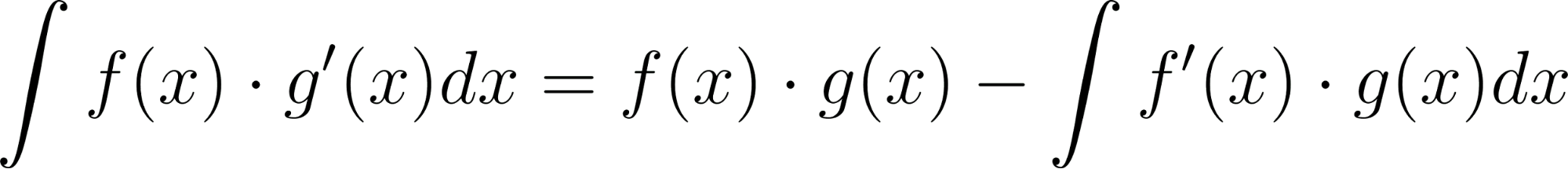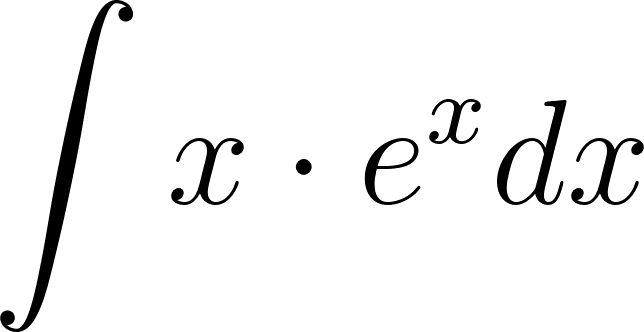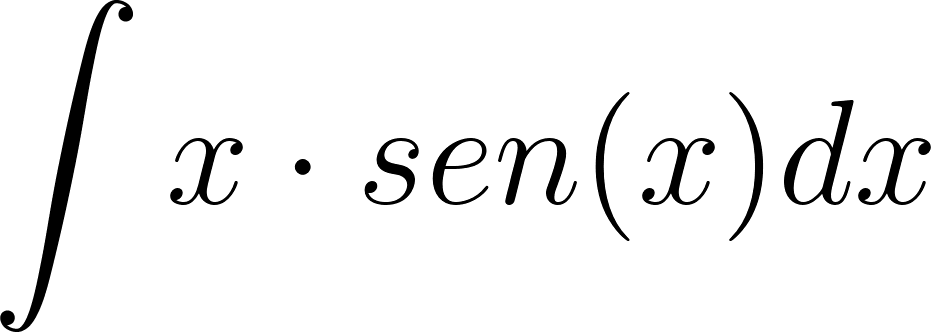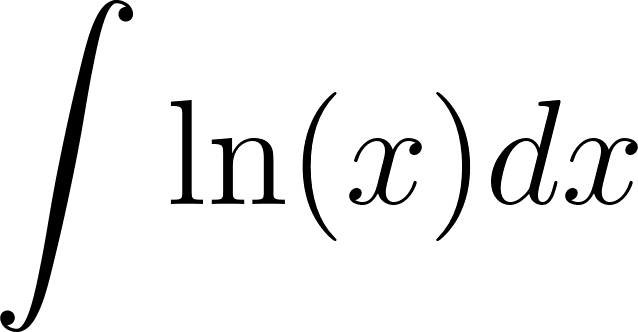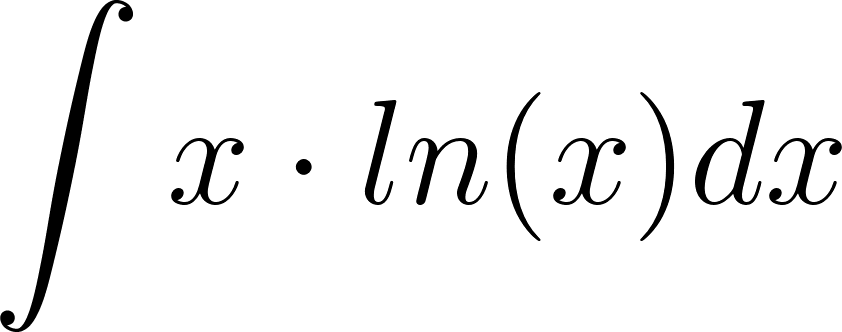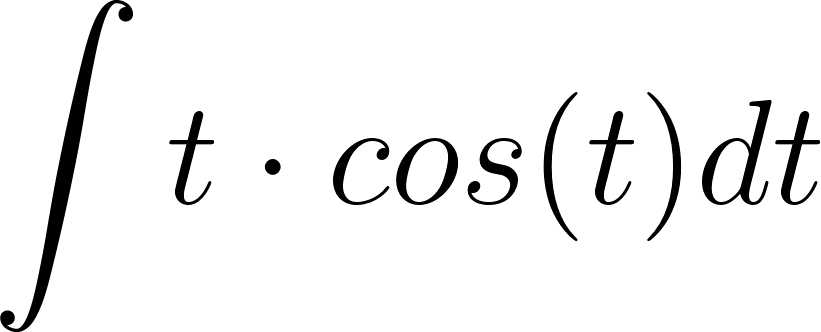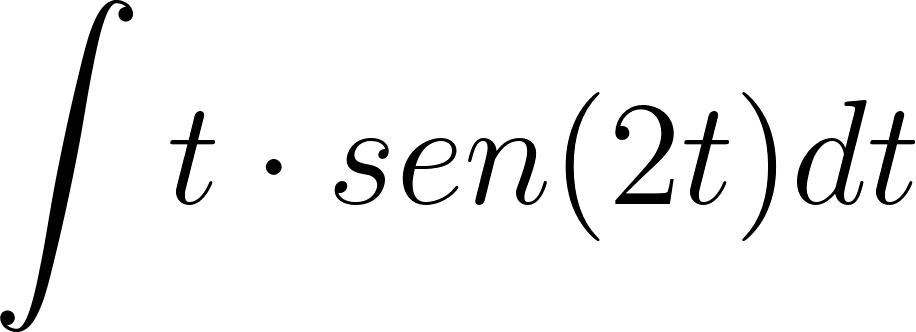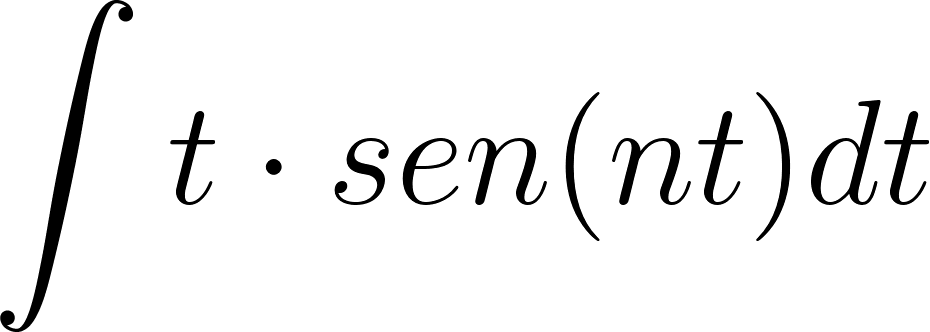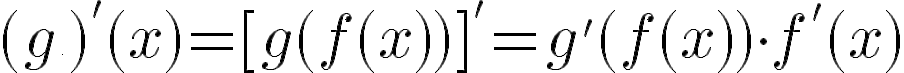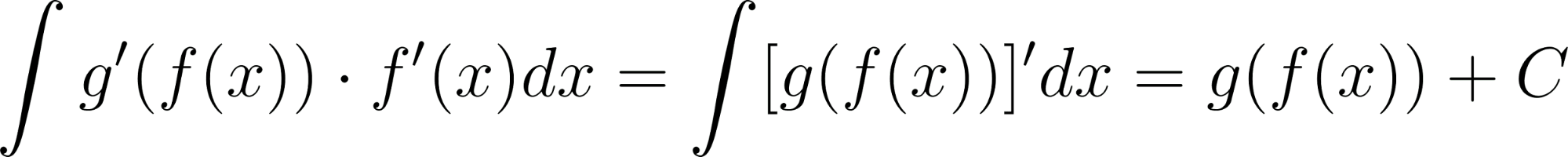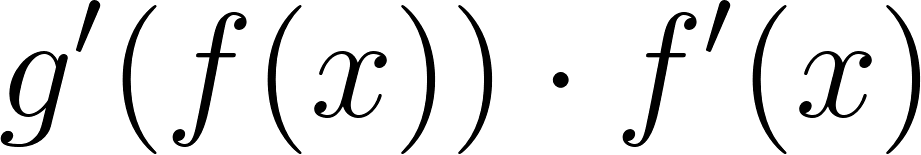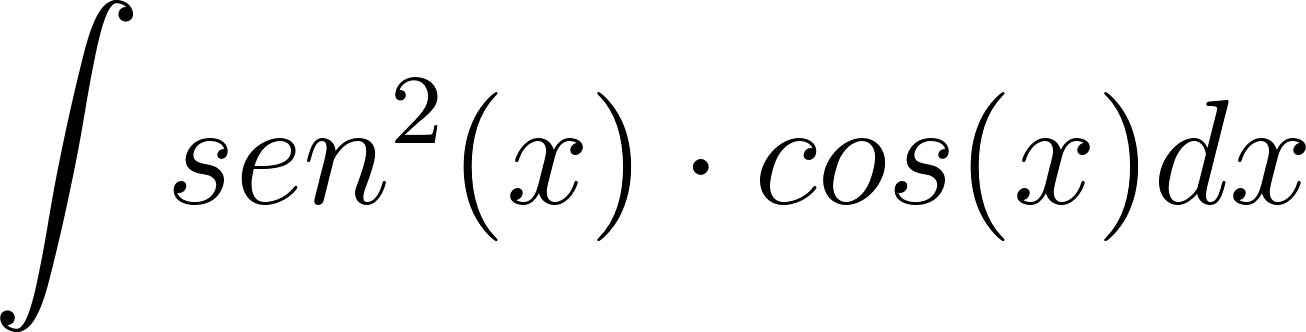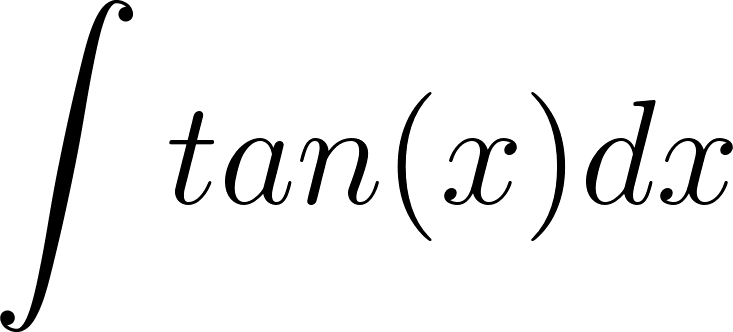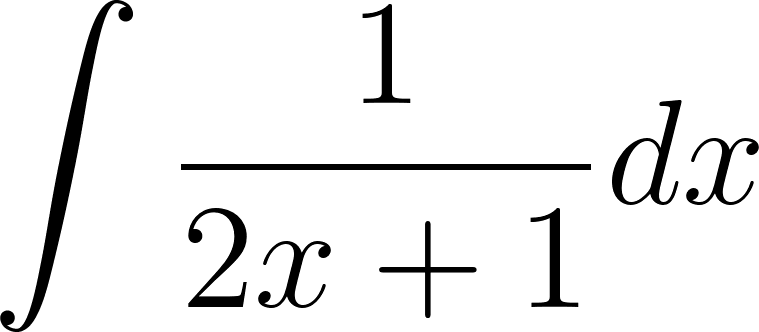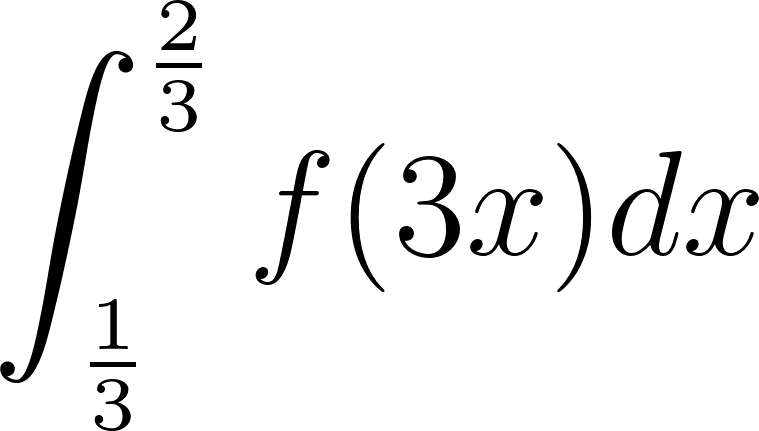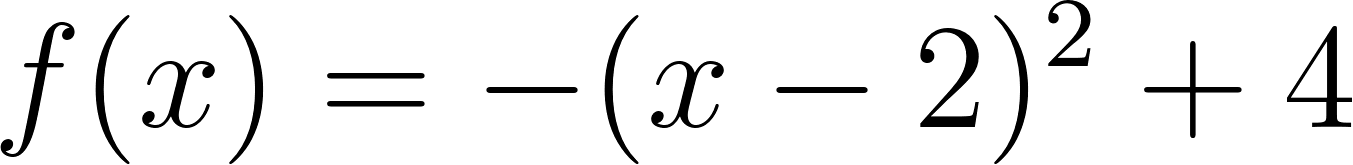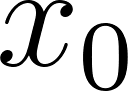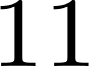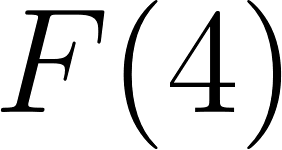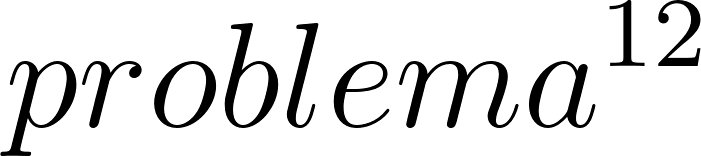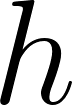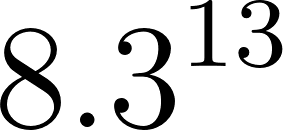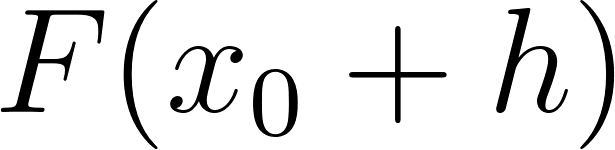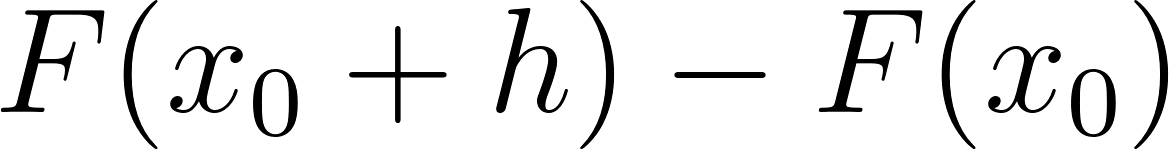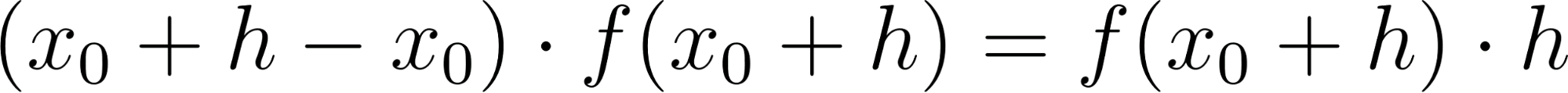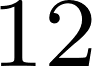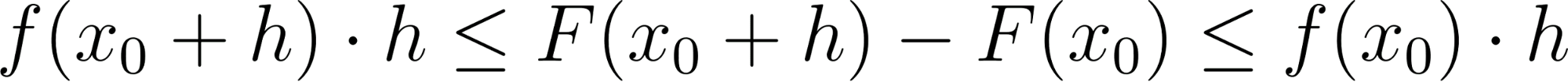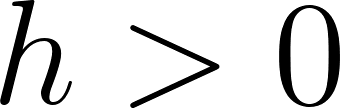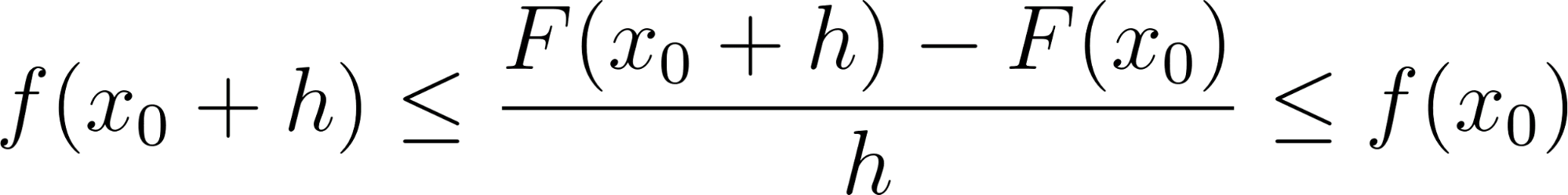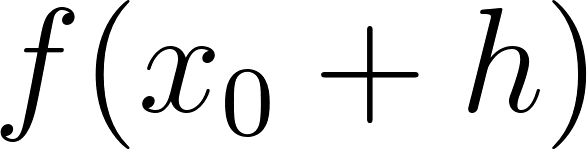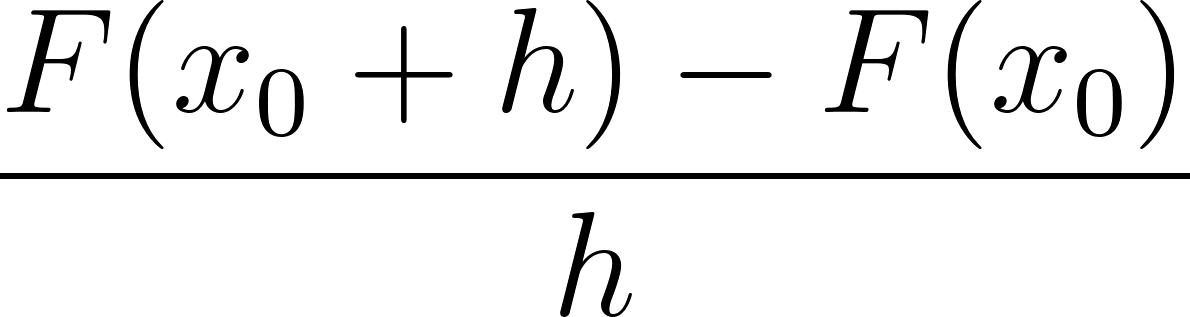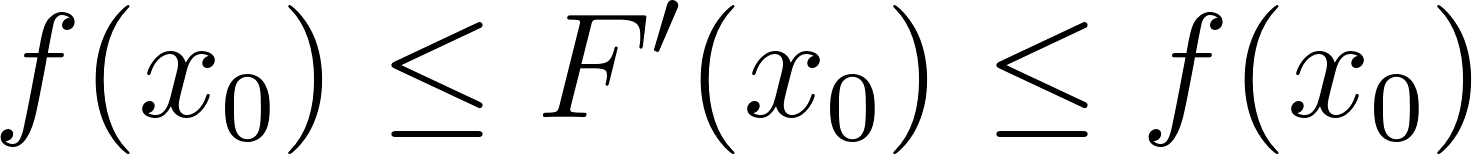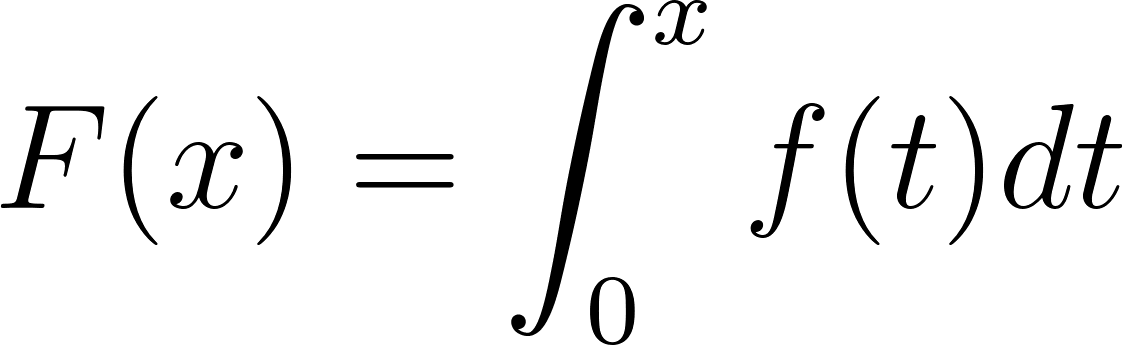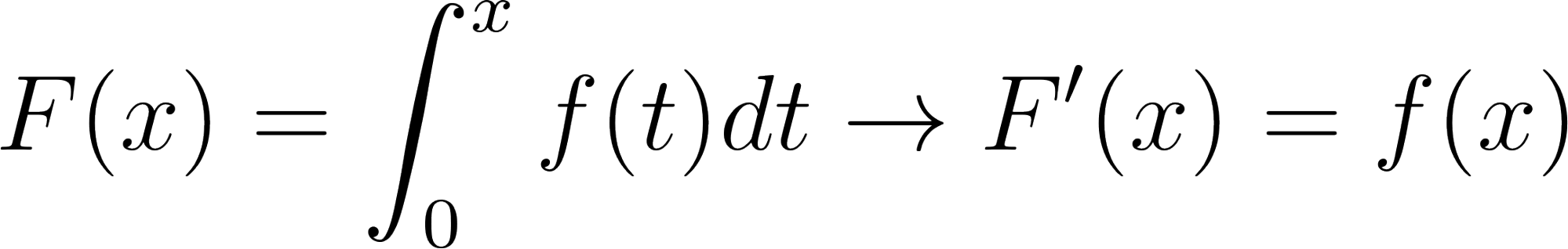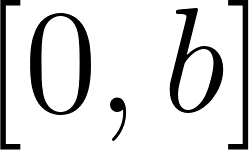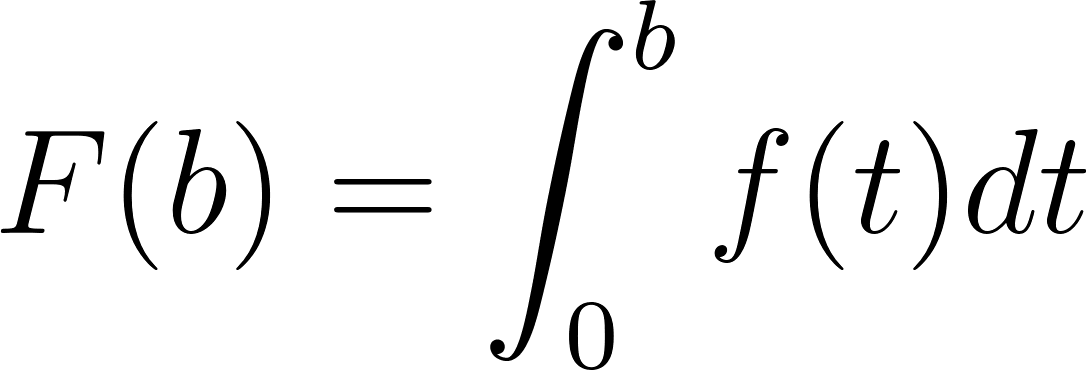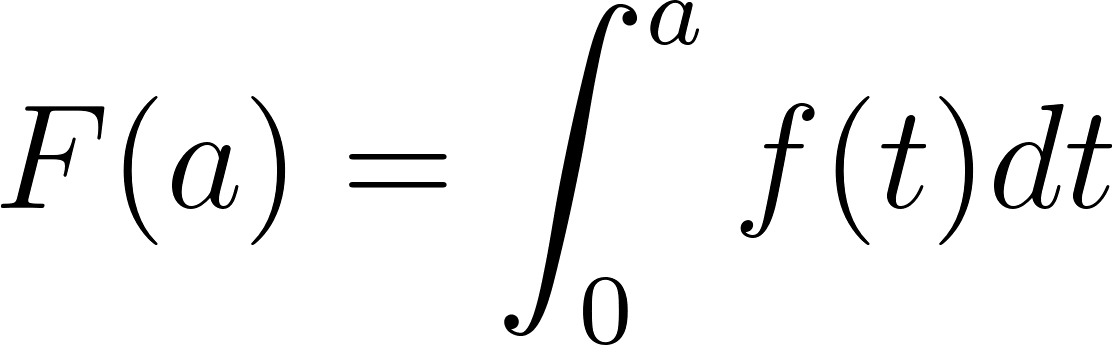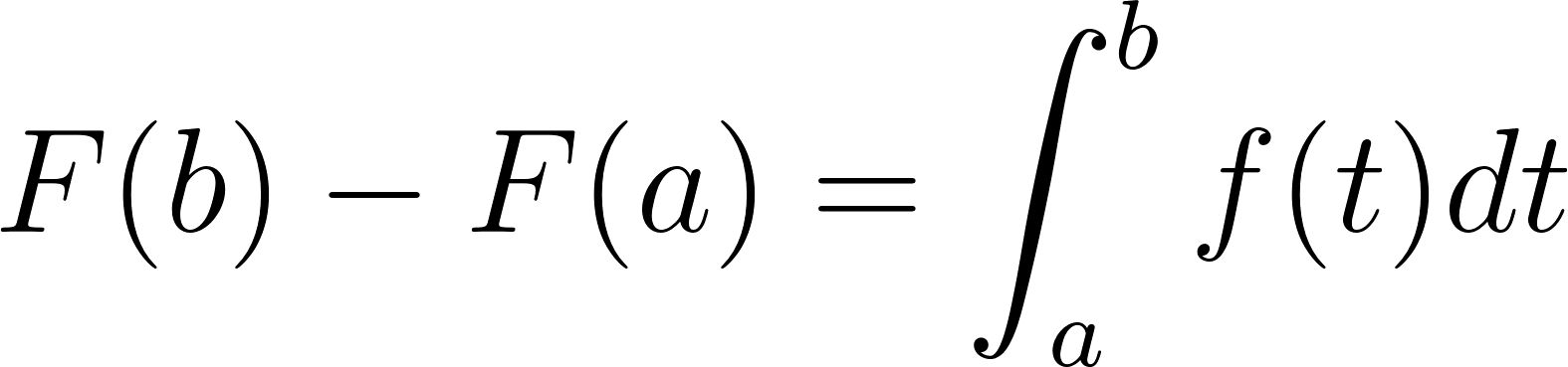Unidad 8
Integrales
Cálculo de áreas y acumulaciones
Objetivos de esta unidad
- Comprender el concepto geométrico de integral como área bajo una curva. Operar con sumas y restas de áreas, logrando resolver situaciones donde estas operaciones son necesarias.
- Comprender las relaciones entre gráficos de posición, velocidad y aceleración. Comprender las relaciones entre caudal y agua acumulada y otras magnitudes físicas.
- Comprender los conceptos de cota, cota inferior, cota superior e intercalación de sucesiones, pudiendo apreciar su importancia como herramientas conceptuales de la matemática (en la justificación de resultados) y en la ingeniería (en el trabajo con mediciones y la estimación de errores).
- Comprender el concepto de integral como un límite de sumas de una sucesión de rectángulos que aproximan el área bajo la curva.
- Comprender que la integral de una función en un intervalo puede ser una función de uno de los extremos del intervalo. Cómo se utiliza esa función en relación al cálculo de área bajo la curva. Por qué una función puede tener muchas primitivas que difieren en una constante. Cómo funciona la regla de Barrow.
- Comprender la relación entre una función, su función integral y su función derivada.
Teoría
Integral Definida
Este video permite interpretar la definición de área bajo una curva, visualizando las sumas superiores e inferiores en GeoGebra.
Propiedades de la integral definida
En estos videos se explican las propiedades de la integral definida:
- Dividiendo el intervalo de integración
- Propiedades de las integrales definidas (gráfico) 2 de 2 | AP Cálculo AB | Khan Academy en Español
Área bajo una curva
Este video muestra cómo se calcula el área bajo la gráfica de una función que toma valores positivos sobre un intervalo.
Algo Teórico
Teorema Fundamental del Cálculo
Leer el Apéndice "el Teorema Fundamental del Cálculo" (página 114 del cuadernillo) para analizar y comprender el teorema. Se recomienda acompañar la lectura del uso del archivo de GeoGebra que se encuentra en el ícono de GeoGebra.TFC Variación: https://www.geogebra.org/m/gvtygfwz
Área entre curvas
Este video muestra cómo se calcula el área de una región encerrada entre los gráficos de dos funciones.
Métodos de integración:
1. 7 - Metodo de integracion por partes - CBC UBA
2. 3 - Metodo de Integracion por Sustitucion - CBC UBA
3. 11 - Fracciones Simples - Explicacion de Metodo CBC UBA
Práctica
Problema 1.
- Grafiquen la región del plano limitada por el eje de abscisas, las rectas verticales de ecuaciones y y la recta de ecuación y calculen su área.
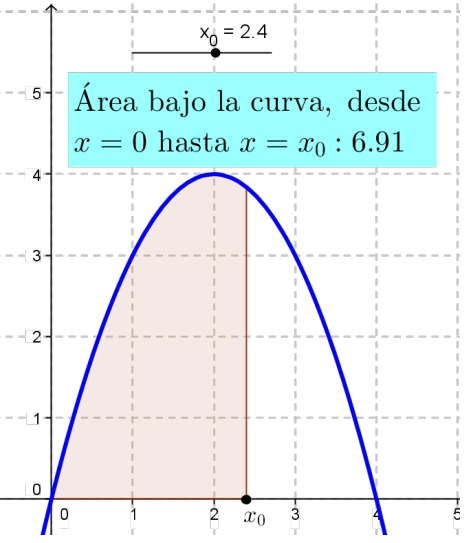
- (De ahora en adelante, abreviaremos toda la descripción de la región anterior y el cálculo de su área, diciendo que se trata del área bajo la gráfica de la función , en el intervalo . Adoptada esta terminología: construyan en GeoGebra, utilizando un deslizador para , un archivo que permita ir variando el valor de entre y y que exhiba en pantalla un cartel que, para cada valor de vaya informando cuál es el área bajo la gráfica de la función , en el intervalo .
Problema 2.
Un compañero de ustedes sugirió la idea de calcular el área bajo la recta genérica de ecuación donde tanto como son mayores que cero, en el intervalo . esta área estará dada por la función .
|
Problema 3. ()
En los problemas anteriores se propuso calcular el área bajo la gráfica de una función en un intervalo, en casos en que los gráficos eran rectas. ¿Pero cómo puede pensarse en cuál será el área bajo la gráfica de una función sobre un intervalo, si la función es, por ejemplo, y el intervalo es ?. |
Para buscar una respuesta, vamos a hacer una exploración con GeoGebra. Investiguen el funcionamiento de los comandos SumaInferior y SumaSuperior, que se pueden ingresar desde la barra de entrada, una vez definida la función (o cualquier otra), respondan:
|
Problema 4. Una cereza del postre para el Problema 3.
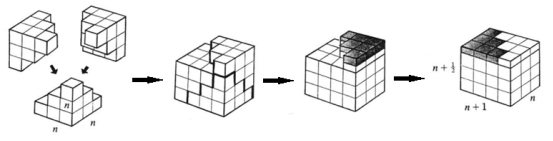
- Se conoce el siguiente resultado para expresar la suma de los cuadrados de los primeros números naturales:
Verifiquen que funciona, para algunos valores de .
- Miren con atención la siguiente demostración sin . ¿Los convence de que la relación es válida para cualquier valor de ?.
- ¿Cómo se puede aprovechar el resultado para terminar de calcular el área del Problema 3?.
Problema 5. En el apéndice de la página 114 hay una explicación que brinda la información esencial para calcular áreas en forma más sistemática (es decir, usando un resultado general). Lean ese material y utilizarlo para calcular las áreas que se describen a continuación:
- Área bajo la gráfica de , en el intervalo .
- .
- .
La figura está tomada del hermoso libro [8]. Proofs without words significa Demostraciones sin palabras. Como se puede apreciar en este ejemplo, se trata de convencerse de una proposición matemática observando fijamente una figura y comprendiendo las relaciones que la misma pone en evidencia. Un modo de lectura que es muy recomendable entrenar, como parte de la formación matemática.
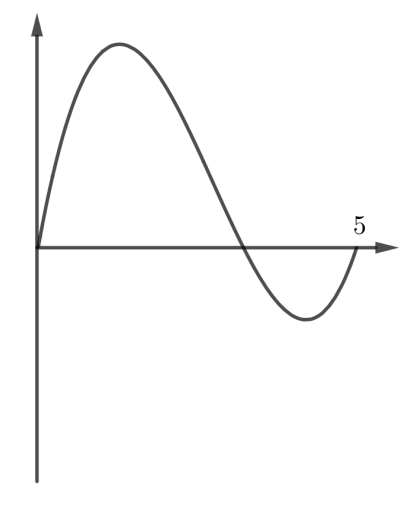
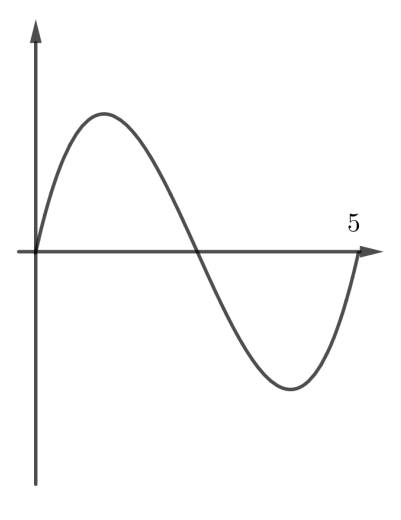
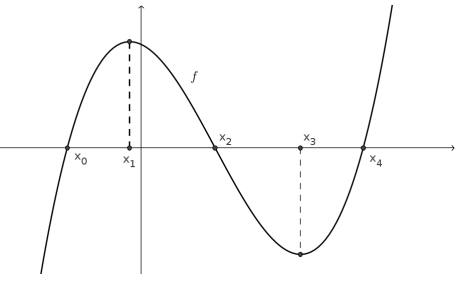
Problema 6. Para cada una de las funciones graficadas, decidan si es positiva, negativa o aproximadamente cero.
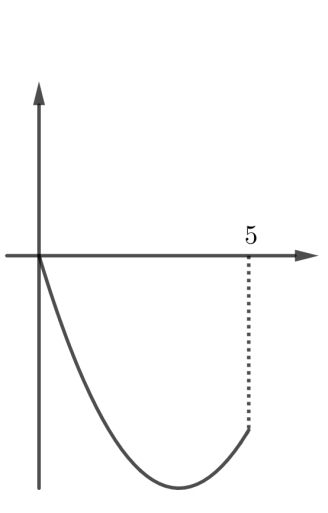
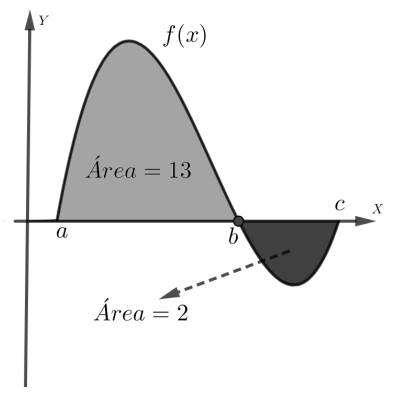
Problema 7. Usen los datos de la figura para hallar los valores de las integrales.
Problema 8. Sean las funciones y tales que:
Calculen las siguientes integrales definidas aplicando las propiedades pertinentes:
- .
- .
- .
- .
- .
- .
- .
- .
Problema 9. Sean dos funciones y integrables y tales que:
.
.
.
Utilicen las propiedades de integrales definidas para calcular:
- .
- .
- .
- .
- .
- .
- .
Problema 10. Sea . Encuentren:
- .
- .
- .
Problema 11. Encuentren las áreas de las regiones comprendidas entre cada una de las siguientes funciones y el :
- , para .
- , para .
- , para .
- , para .
- , para .
- , para .
Problema 12. Hallen el área encerrada entre las gráficas de las funciones y . Sugerencia: Hallen primero los puntos de intersección entre cada par de funciones y determinen los límites de integración.
- .
- En el primer cuadrante.
- .
- Entre .
- .
Problema 13. Tracen la gráfica de la función . encuentren el área encerrada por la gráfica y el eje en el intervalo . Luego, calculen e interpreten el resultado obtenido en términos de área.
Problema 14. ()
- Lean atentamente la siguiente descripción y construyan un gráfico con todos los objetos que se detallan.
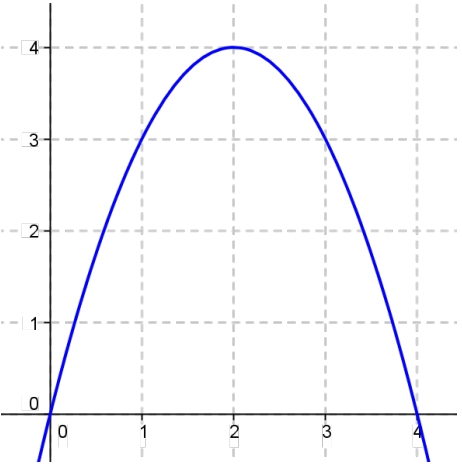
- es una función definida sólo para , dada por la fórmula:
- es la recta tangente al gráfico de en el punto en que alcanza su valor máximo.
- Calculen el área de la región del primer cuadrante limitada por el eje , el gráfico de y la recta $.
Problema 15. Hallen el área de la región limitada por los gráficos de las funciones y dadas a continuación, escribiendo todos los cálculos que permiten obtenerla.
Problema 16. Calculen el área de la región limitada por el gráfico de la función y el eje , entre los valores de en los que tiene sus extremos locales, siendo .
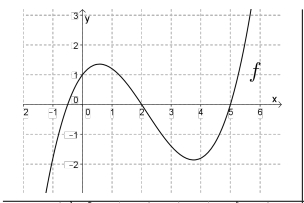
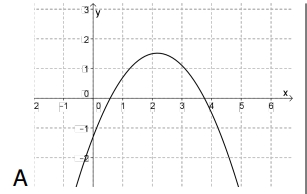
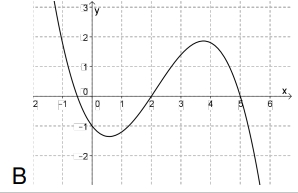
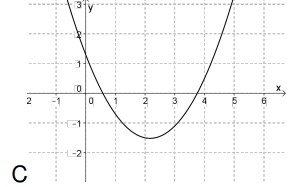
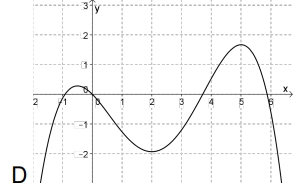
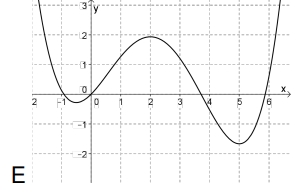
Problema 17. En la siguiente serie de gráficos el primero corresponde a una función , decidan cuál de los demás gráficos puede ser el de la derivada de y cuál, el de una primitiva de . Justifiquen la elección de los gráficos y por qué descartaron los restantes.
Función | ||
Problema 18. Observando el gráfico de la función , y llamando a una primitiva de (es decir, ).
|
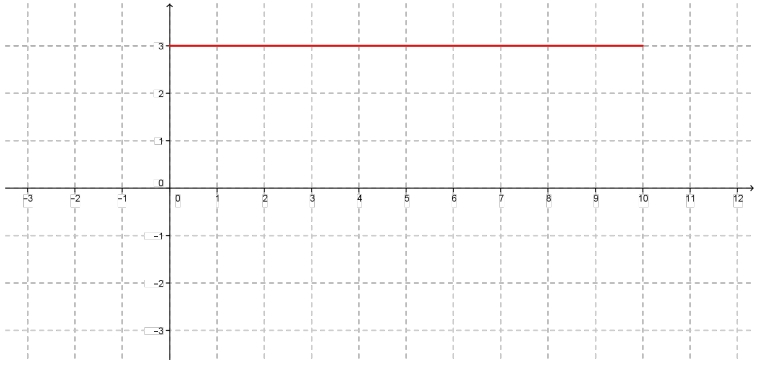
Problema 19. El siguiente es un gráfico de la velocidad de un automóvil en función del tiempo.
Realicen un posible gráfico para la posición en función del tiempo.
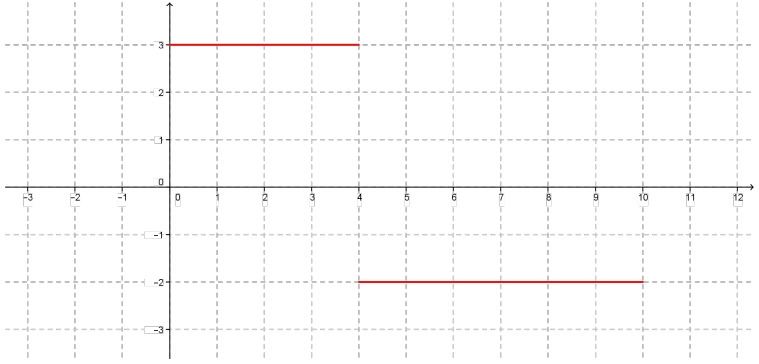
Problema 20. Como en el problema anterior, el siguiente es un gráfico de la velocidad de un automóvil en función del tiempo.
Realicen un posible gráfico para la posición en función del tiempo.
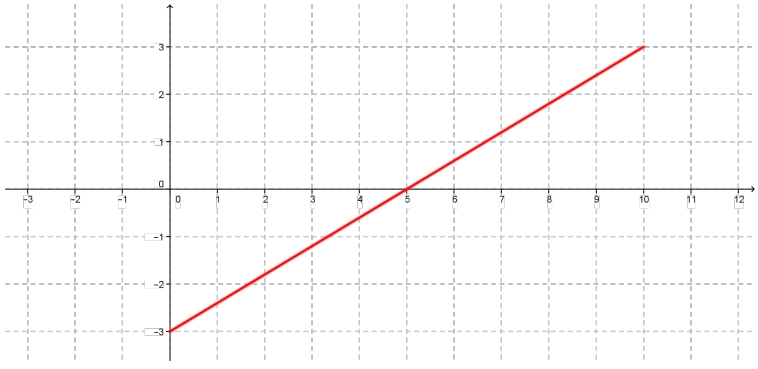
Problema 21. Una vez más, el siguiente es un gráfico de la velocidad de un automóvil en función del tiempo.
Realice un posible gráfico para la posición en función del tiempo.
Problema 22. Un ciclista realiza una prueba de velocidad recorriendo sólo 100m. Una buena descripción de la velocidad (medida en metros por segundo) en función del tiempo (medido en segundos) viene dada por la fórmula.
- ¿Qué distancia recorre entre los 6 y los 9 segundos de su recorrido?.
- ¿Cuánto tiempo le lleva recorrer los 100m?.
Problema 23. () un vehículo inicia un recorrido en línea recta, desde una posición que consideramos el origen () y su velocidad en función del tiempo viene dada (en ciertas unidades) por .
- ¿Qué distancia recorrió en el intervalo que va de a ? (Pueden efectuar los cálculos en GeoGebra, pero se pide expresar por escrito cuál es el cálculo que se debe resolver).
- ¿En qué momento, aproximadamente, comenzó a regresar?.
- ¿Cuánto tiempo le llevó regresar al punto de partida?.
- ¿Qué distancia habrá recorrido en total?.
Problema 24. Sabemos que la velocidad de un móvil está dada por la ecuación .
- Prueben que parte del reposo.
- Halle la ecuación de la posición del móvil.
- Hallen la distancia recorrida en los primeros 5 segundos.
Ayuda:
Problema 25. Una pileta se está llenando con agua mediante una canilla. En un momento dado (que tomaremos como tiempo 0) se comienza a cerrar la canilla hasta que se llega a cerrar totalmente. La cantidad de agua que contiene la pileta (en litros) en función del tiempo (minutos) está dada por la función:
- ¿Cuál es el tiempo en el cual la canilla se cierra totalmente?.
- ¿Cuántos litros de agua tenía la pileta cuando se comenzó a cerrar la canilla?.
- ¿Cuántos litros de agua entraron a la pileta desde que se empezó a cerrar la canilla hasta que se terminó de cerrar?.
- ¿Cuál es la cantidad media (o promedio) de litros por minuto que entraron a la pileta desde que se comenzó a cerrar la canilla hasta que se terminó de cerrar?.
- ¿Cuál es la cantidad media de que entraron a la pileta entre el minuto y el minuto después de que se empezó a cerrar la canilla?.
- ¿Cuál es la cantidad exacta de que estaban saliendo por la canilla a los cuatro minutos de haber empezado a cerrarla?.
- ¿Podrías definir una función que describa la cantidad de agua que salía por la canilla en cada momento entre que se empezó y se terminó de cerrar?.
Problema 26. Ante la misma situación que el problema anterior, pero con otra pileta y otra canilla, sabemos que la función que describe la cantidad de agua por minuto que sale por la canilla desde que se comienza hasta que se termina de cerrar está dada por:
- ¿Cuál es el tiempo en el cuál la canilla se cierra totalmente?.
- ¿Cuántos litros de agua entraron en la pileta durante el período en que se fue cerrando la canilla?.
- ¿Cuántos litros de agua entraron en la pileta durante los primeros 7 minutos en que se estaba cerrando la canilla?.
- ¿Podrías describir una fórmula que para cada instante calcule la cantidad de agua que entró en la pileta desde que se comenzó a cerrar la canilla?.
- Si cuando se comenzó a cerrar la canilla la pileta contenía litros de agua, definan una fórmula que calcule la cantidad de agua que contenía la pileta en cada instante entre que se empezó y se terminó de cerrar la canilla.
Problema 27. Un río desemboca en un embalse. La cantidad de agua medida en que llega por el río entre dos momentos determinados está descrita por la función:
- Identifiquen cuáles son esos dos momentos y calculen la cantidad de agua que entra al embalse durante el tiempo transcurrido entre ellos.
- Determinen si es cierto que durante ese período cada vez entra más agua.
Problema 28. Hallen el área de la región limitada por los gráficos de las funciones y , escribiendo todos los cálculos que permiten obtenerla.
Problema 29. Lean el siguiente recuadro:
El cálculo de la primitiva de una función en un intervalo que suele anotarse como puede ser difícil en casos de funciones que sean producto de funciones más simples. En estos casos podemos apelar a una fórmula que se basa en la propiedad de la derivada del producto de dos funciones: Está fórmula se puede integrar aplicándose propiedades de la integral, obteniéndose como resultado: que puede expresarse también como: Este método es conocido con el nombre de Integración por partes. La técnica consiste en hallar unas y adecuadas que permitan descomponer la función de la que se quiere hallar la primitiva, de manera que la nueva integral que genere sea más fácil de resolver. |
Dicho esto, aquí tienen una linda cantidad de integrales para entretenerse una tarde de lluvía.
Problema 30. Lean el siguiente recuadro:
Otro recurso para encontrar primitivas de algunas funciones es el conocido como Método de integración por sustitución. Este método es aplicable, en algunos casos, cuando el integrando (la función de la que se desea conocer una primitiva) es una composición de funciones. Y se basa simplemente en la regla de la cadena para derivar funciones compuestas (ver Problema 37 de la unidad de Derivadas). La idea es la siguiente. Sabemos, por la regla de la cadena que: Por lo tanto, como las primitivas de la derivada de una función son esa misma función (más una constante real arbitraria), resulta: Entonces este recurso se puede utilizar cuando uno reconoce que el integrando tiene la estructura para ciertas funciones y que consigue identificar. |
Las siguientes primitivas pueden calcularse mediante el método de sustitución:
Problema 31. Sea
Calculen .
Apéndice
Teorema fundamental del Cálculo
En una actividad desarrollada en clase, nos propusimos calcular el área bajo el gráfico de la función , en un intervalo. Vamos a estudiar una solución general del problema, guiándonos por un ejemplo. Consideremos la función:
Definida en el intervalo , según se ve en la FIGURA 8.1
Figura 8.1: Gráfico de |
En el archivo TFC.ggb se puede manipular un gráfico como el de la Figura .
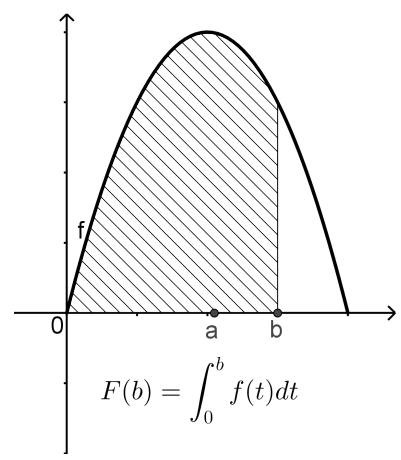
Figura 8.2: Área desde hasta . |
Al mover el deslizador el área bajo la curva va cambiando: crece cuando movemos el deslizador hacía la derecha y decrece cuando lo movemos hacia la izquierda. Esto significa que el área bajo la curva varía con y, por lo tanto, es función de .
Se recomienda acompañar esta lectura con el archivo TFC abierto y “al alcance de la mano”.
Si llamamos a esa función, podemos explicar cómo está definida, aunque todavía no conozcamos su fórmula:
es el área bajo el gráfico de , entre y . |
Con esta idea está bastante claro que si conociéramos la fórmula de la función estaríamos en condiciones de conocer el área bajo la gráfica de , en cualquier intervalo. En particular, nos daría el área bajo toda la curva.
El objetivo de este apunte es deducir informalmente la idea genial que resuelve el Y el punto de partida consiste en investigar cómo varía la función .
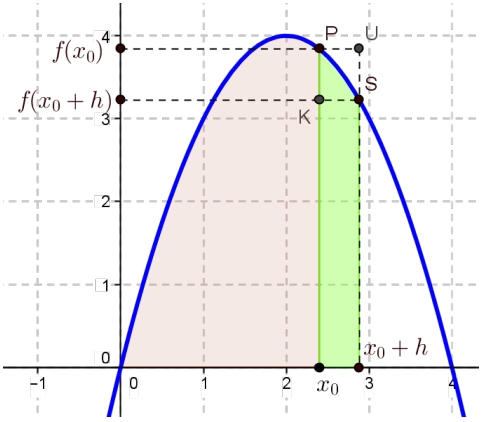
Para eso, consideremos una posición fija del punto , como mostraba la Figura 8.2 y una posición corrida una distancia pequeña hacía la derecha, como muestra la Figura
Figura 8.3: Área hasta y un poquito más. |
Con esta interpretación de las figuras tenemos:
Es el área de la región sombreada, desde hasta . | |
Es el área de la región sombreada, desde hasta . Por lo tanto, | |
Es el área de la franja verde agregada |
Observen que esta franja verde agregada es mayor que el rectángulo de vértices y , pero más pequeña que el rectángulo de vértices y . Expresemos las áreas de esos rectángulos, en relación a los valores que nos da la función :
Área del rectángulo : | |
Área del rectángulo : |
Esta idea se atribuye al inglés Isaac Newton y al alemán Gottfried Wilheim Leibniz, que vivieron y desarrollaron sus investigaciones durante los siglos XVII y XVIII. A pesar de trabajar cada uno por su cuenta, llegaron a las mismas conclusiones. Conscientes de la importancia histórica de esta idea, sostuvieron fuertes disputas para atribuirse el mérito del descubrimiento. Muchos historiadores de la ciencia piensan que no hubo ninguna situación de plagio entre ellos, sino que -simplemente- vivieron en una época en que la Humanidad había acumulado los saberes previos necesarios para que esta idea pudiera surgir. A favor de este punto de vista está la célebre frase que se atribuye a Newton: “Si he logrado ver más lejos, ha sido porque he subido a hombros de gigantes”.
También pueden manipular el archivo TFCVariacion.ggb.
Por lo tanto, como el área verde está comprendida entre esos dos rectángulos resulta:
Dividiendo por :
Ahora, si queremos estudiar la variación de la función debemos considerar variaciones muy pequeñas de su variable. Esta idea ya la pusimos en juego varias veces y consiste en considerar el límite cuando tiende a . En ese caso, la expresión , que está a la izquierda de la desigualdad anterior resulta ser y la expresión que está en el medio resulta ser la derivada de en , es decir:
De donde
Como este mismo razonamiento valdría en cualquier lugar que eligiéramos el punto , resulta que vale en realidad para cualquier punto en el intervalo que nos interesa.
Lo que hemos descubierto es que la función que da el área bajo la curva de la función es una función que tiene a por derivada. Así, el problema de calcular el área bajo la curva de se convierte en el problema de encontrar una función cuya derivada sea . Una función así se llama una primitiva de . Así, si es una primitiva de entonces es la derivada de .
Leibniz propuso un símbolo para referirse a la función y ese símbolo se ha instalado completamente, de manera que podrán encontrarlo en cualquier libro de matemática, física, ingeniería, etc. en el que se mencione esta teoría.
Con esta simbología, este resultado, que recibe merecidamente el pomposo nombre de Teorema fundamental del Cálculo, podría escribirse así:
.
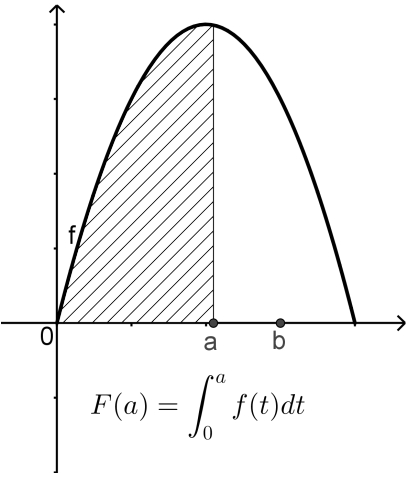
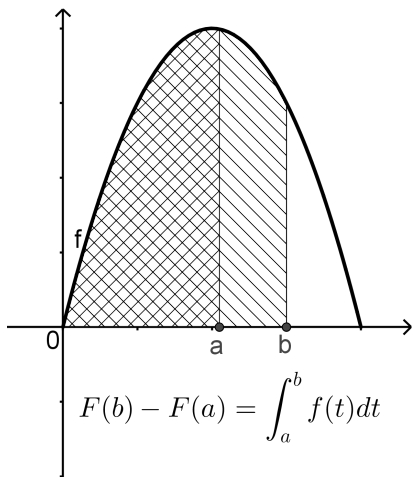
El Teorema fundamental del Cálculo permite calcular el área bajo la gráfica de en el intervalo . Pero, en realidad, permite calcular dicha área en cualquier intervalo . En efecto, observando la siguiente figura, resulta que el área bajo la gráfica de en el intervalo es la diferencia entre el área que va de hasta y la que va de hasta :
Para seguir estudiando en biblioteca
En esta sección recomendamos algunos libros e indicamos problemas que está bueno hacer para seguir practicando y aprendiendo.
Como mencionamos en la misma sección de la Unidad anterior, el libro Matemáticas para administración y economía de Ernest Haeussler et all. [5] es una excelente fuente de problemas. Recomendamos los problemas de la sección de problemas 14.10 de las páginas 673 y siguientes.
Los capítulos 5, 6 y 7 del libro Cálculo Aplicado de Deborah Hughes-Hallett et al. [7] constituyen la mejor introducción al tema de integración con excelentes explicaciones y problemas para practicar y poder evaluar si comprenden el tema. Es altamente recomendable dedicarle tiempo a su lectura. Todavía no hay ejemplares en biblioteca pero pueden conseguir copias de esos capítulos en fotocopiadora.