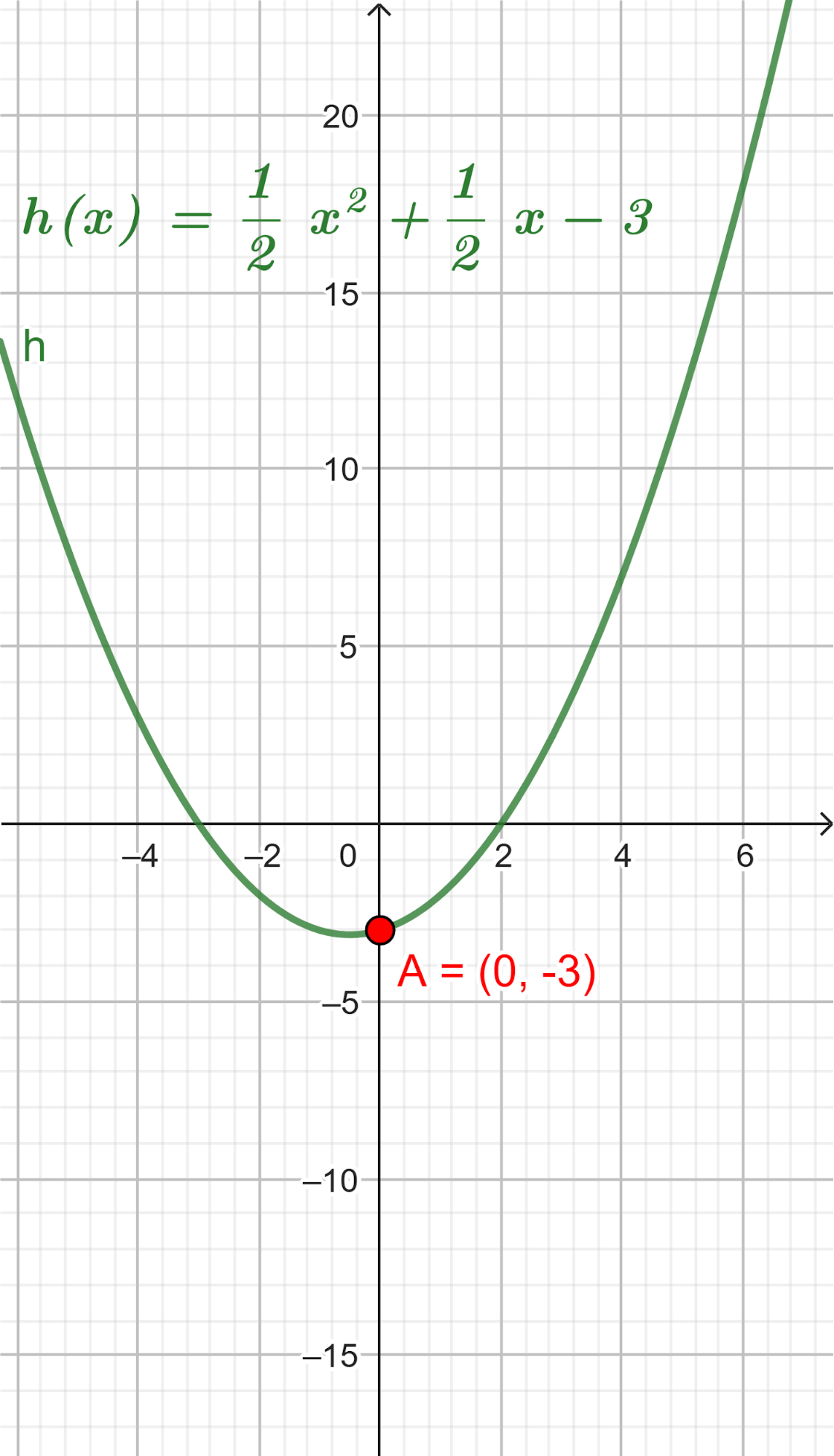
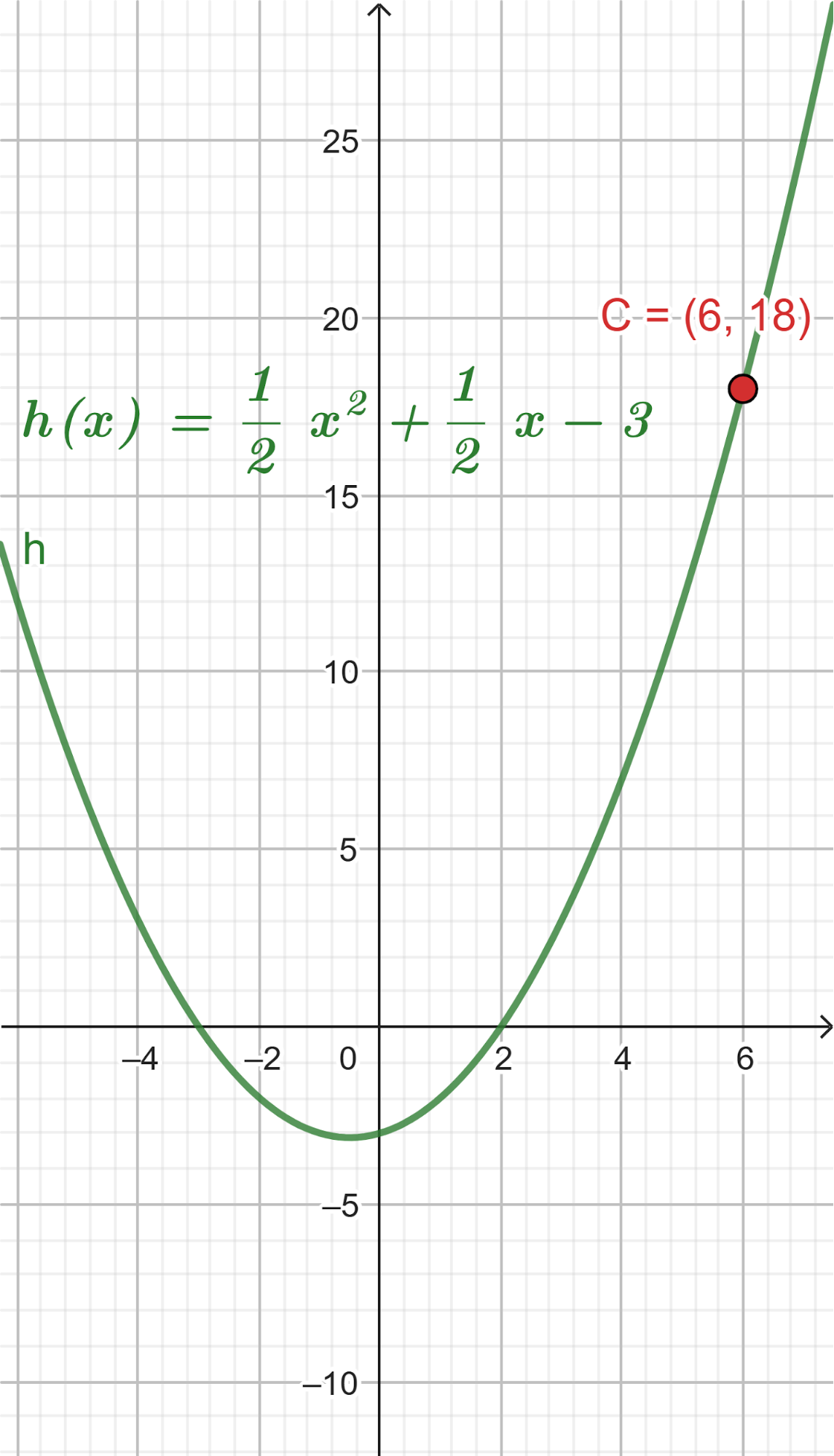
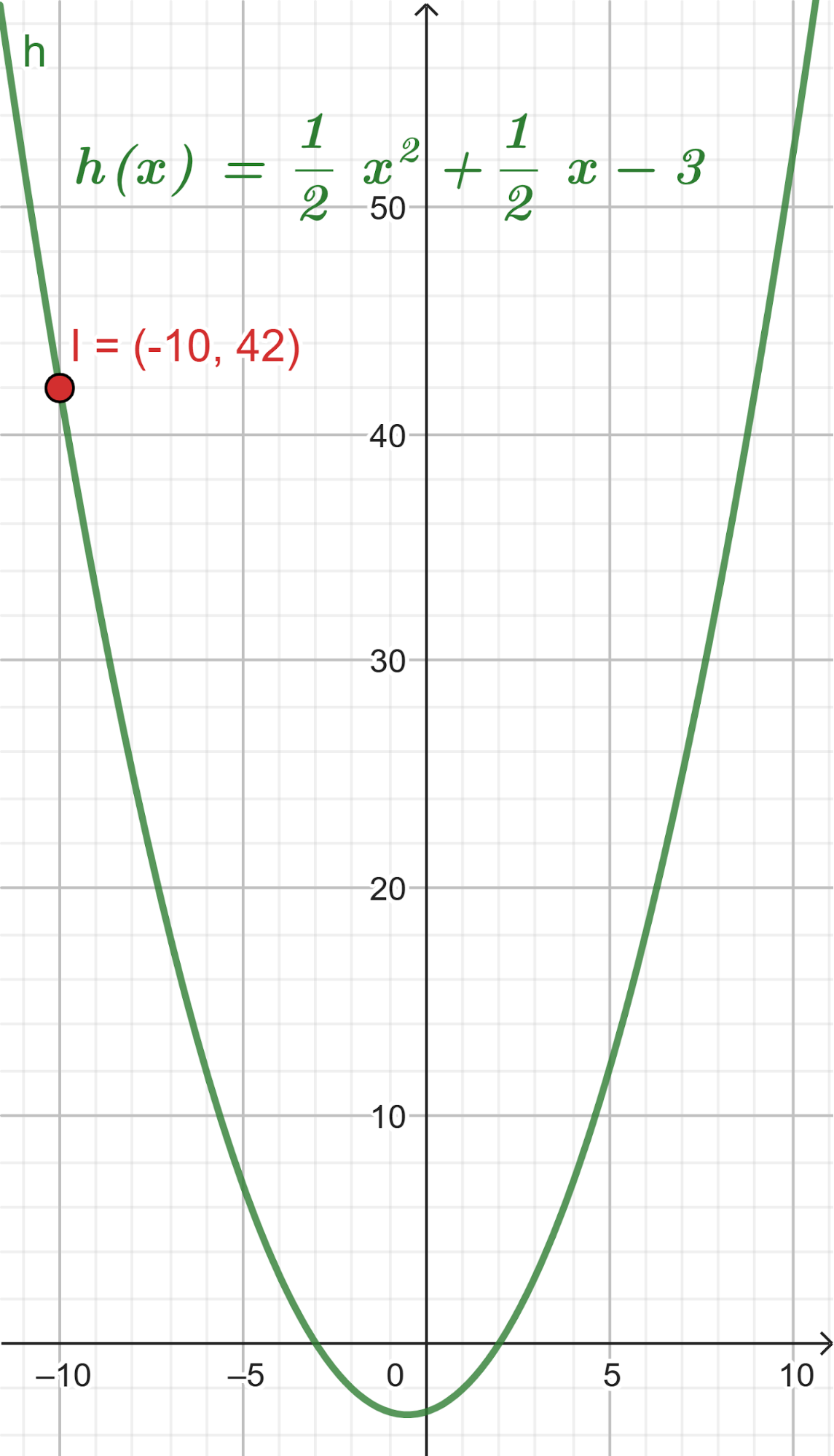
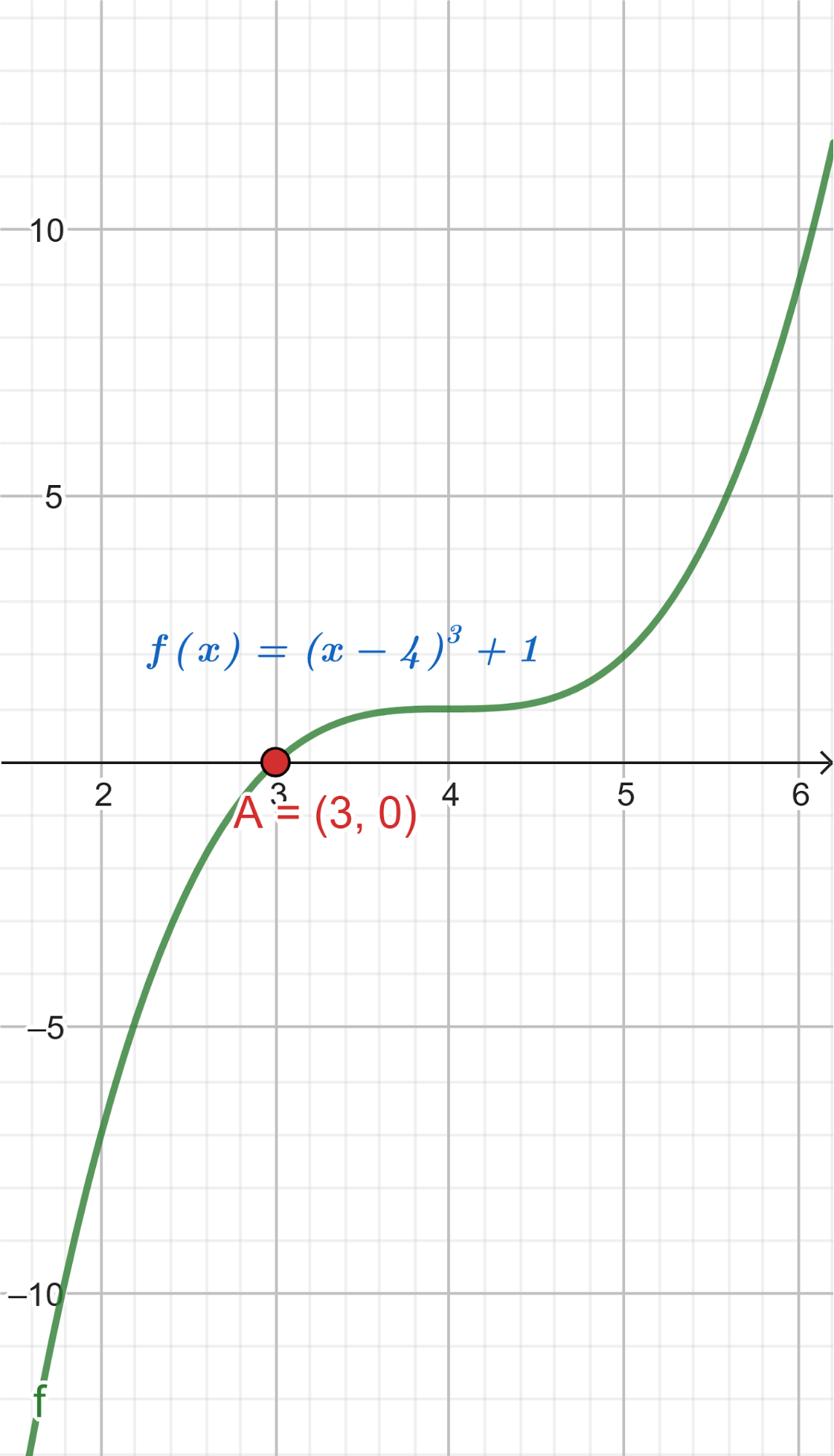
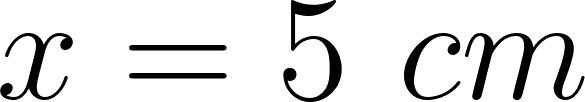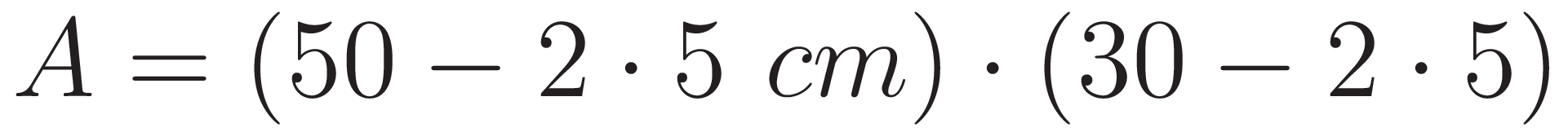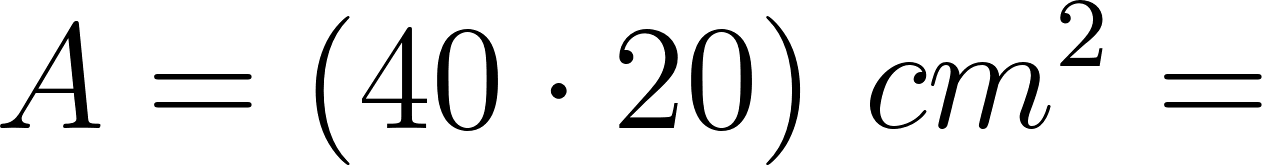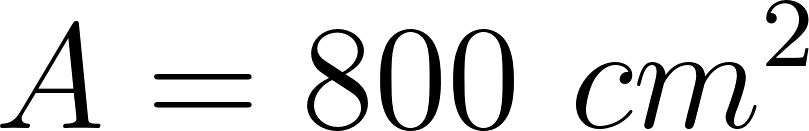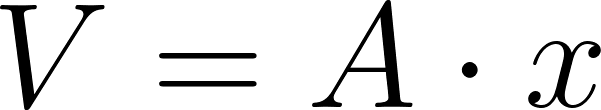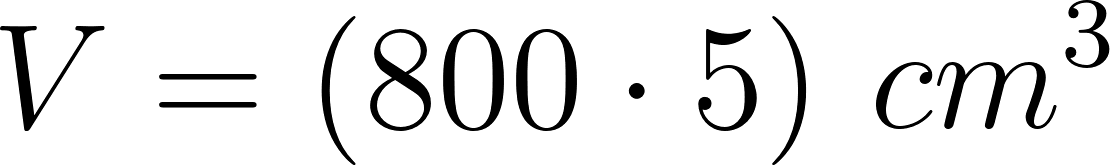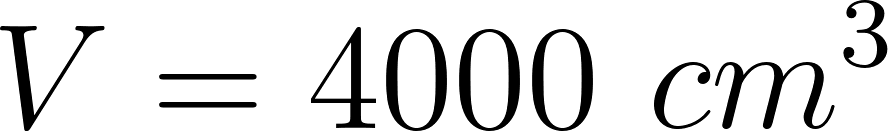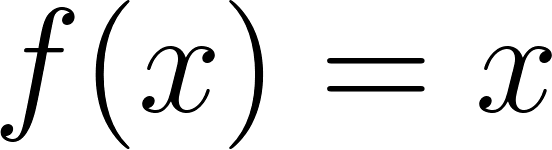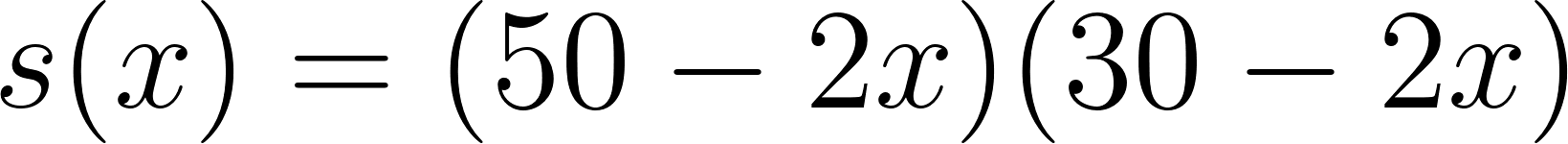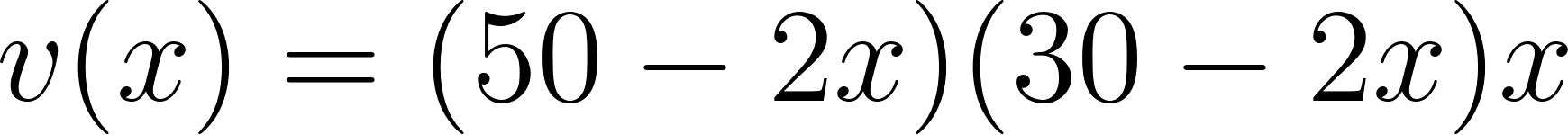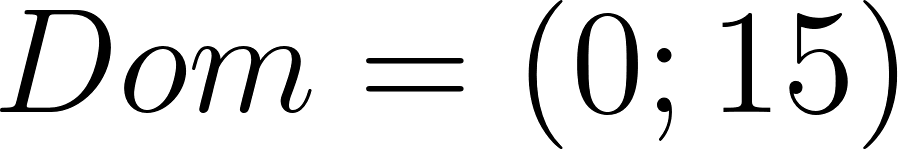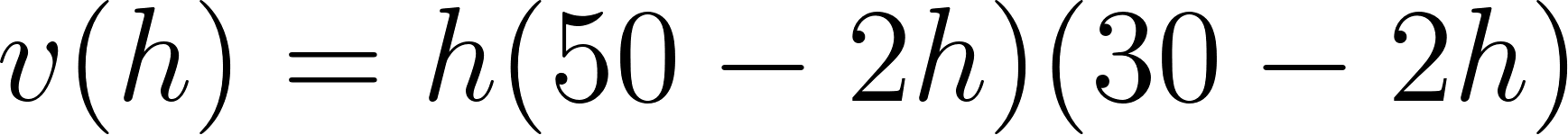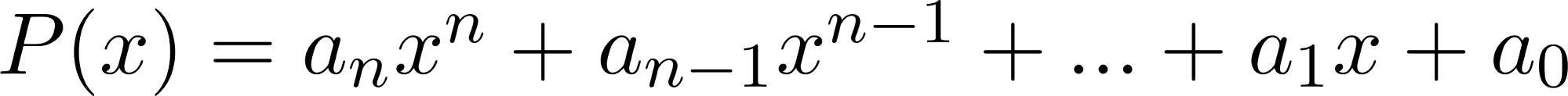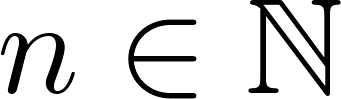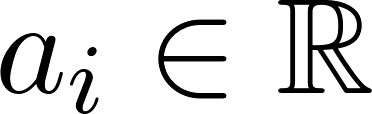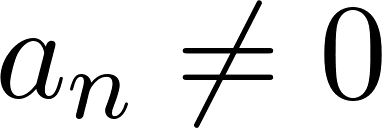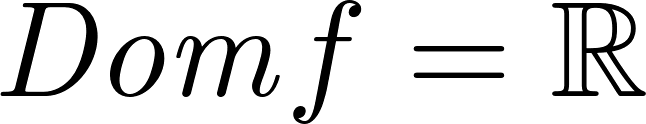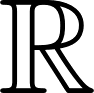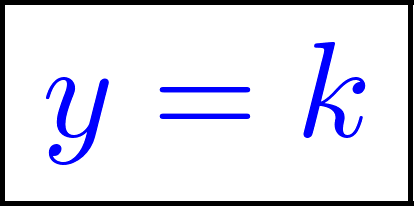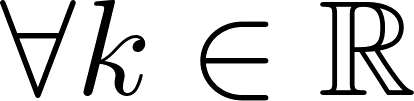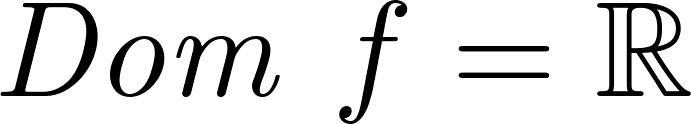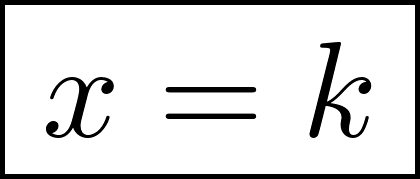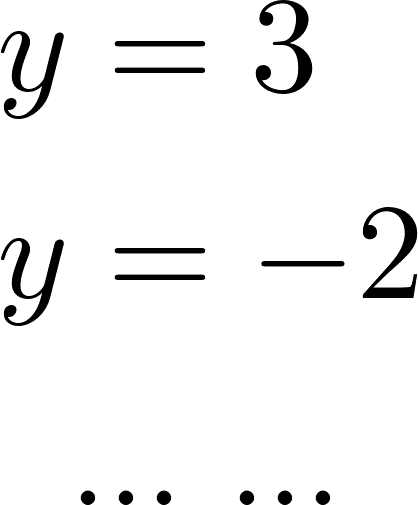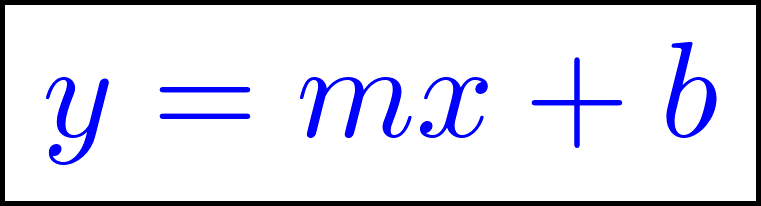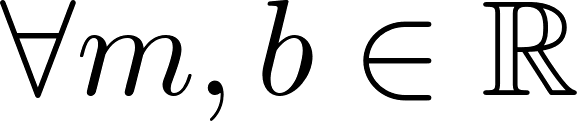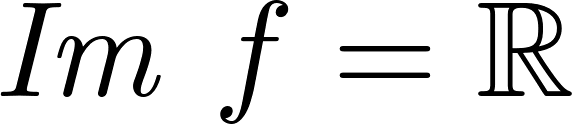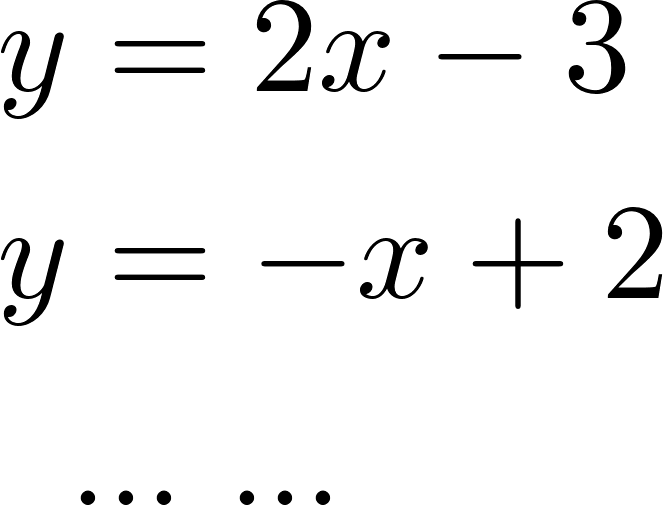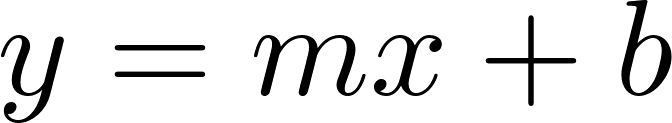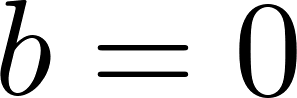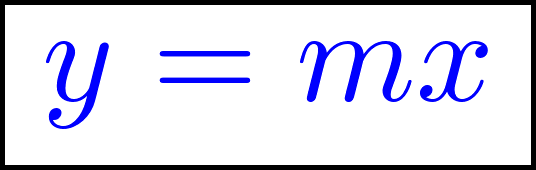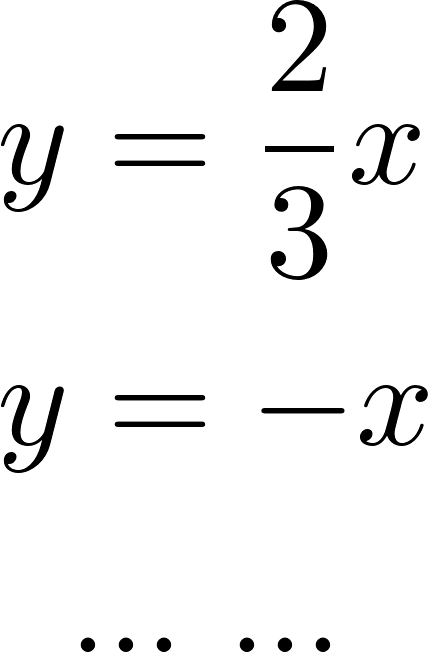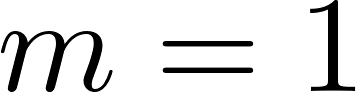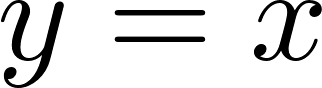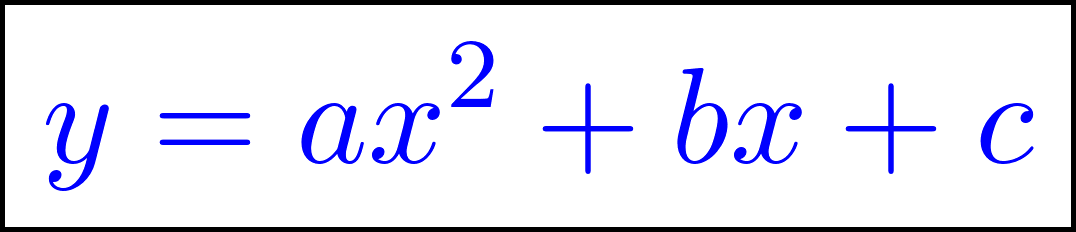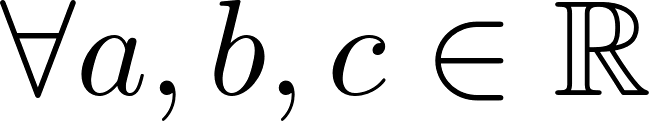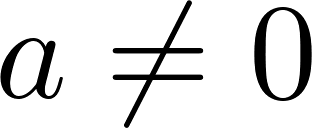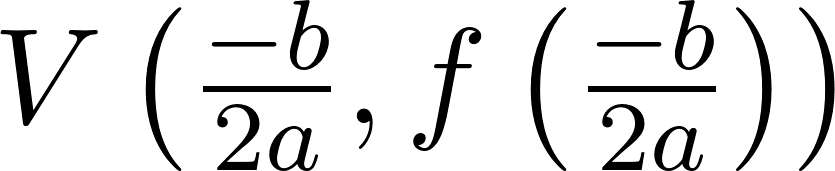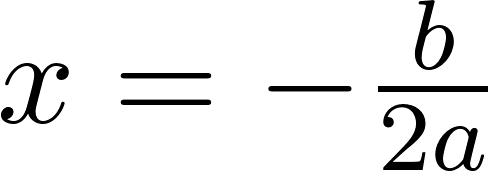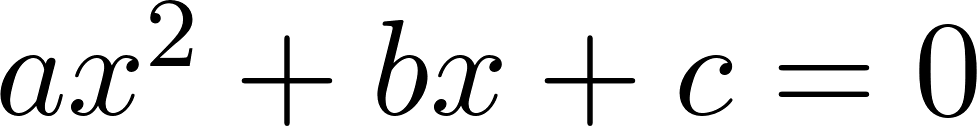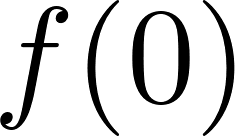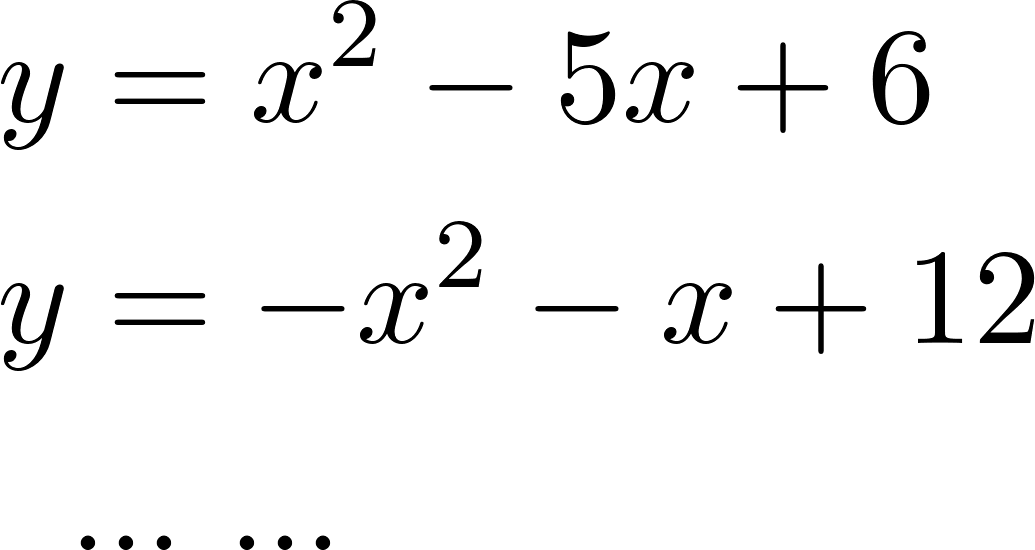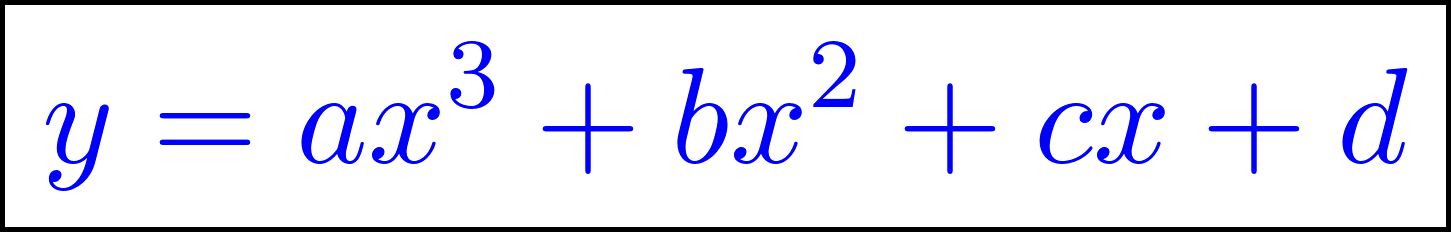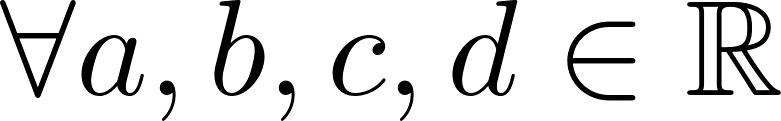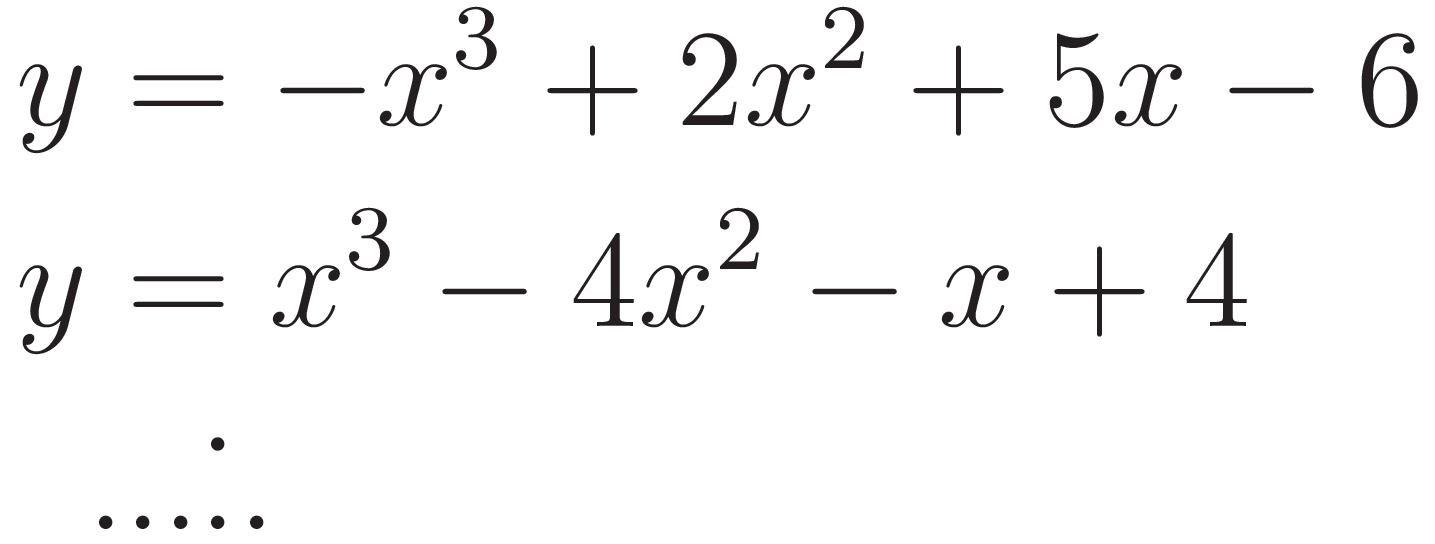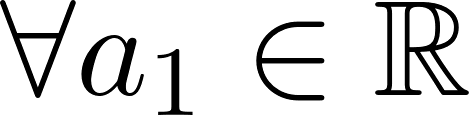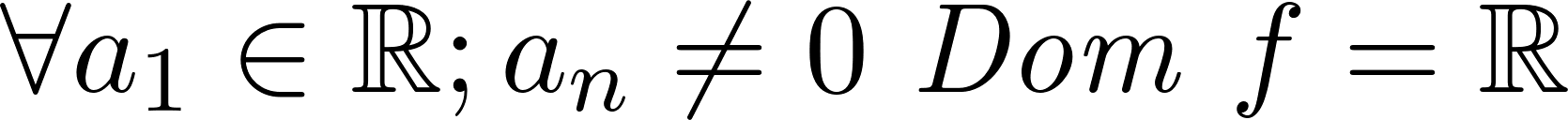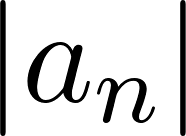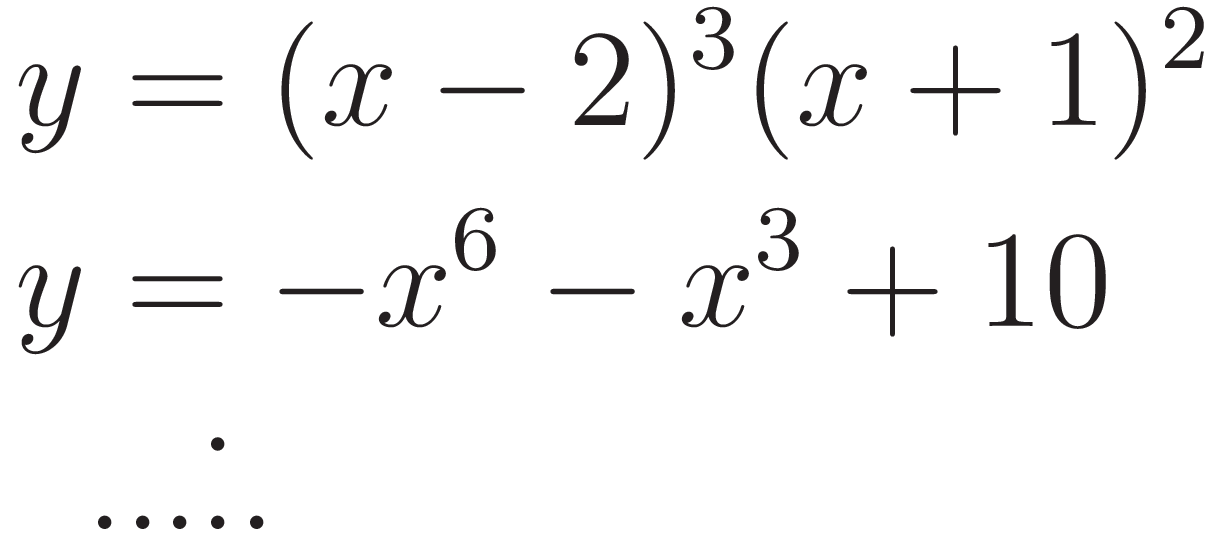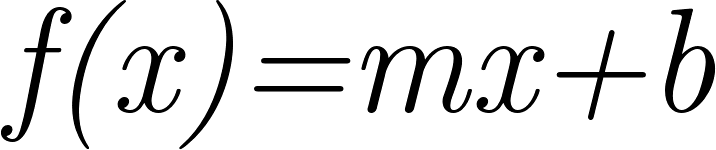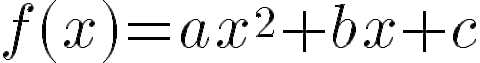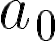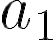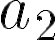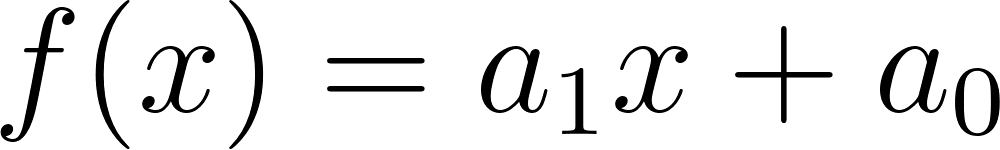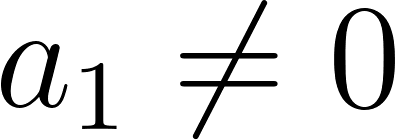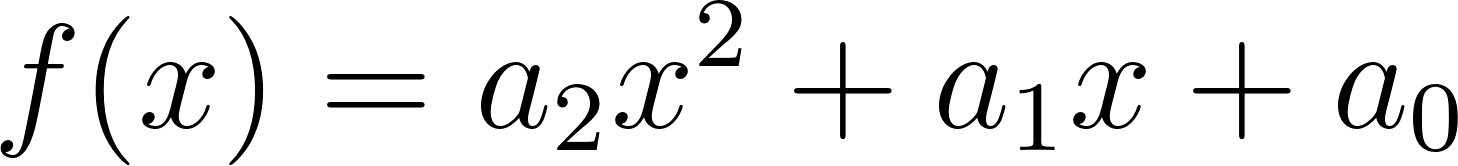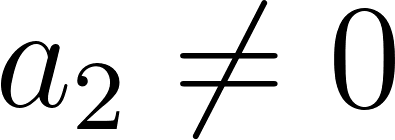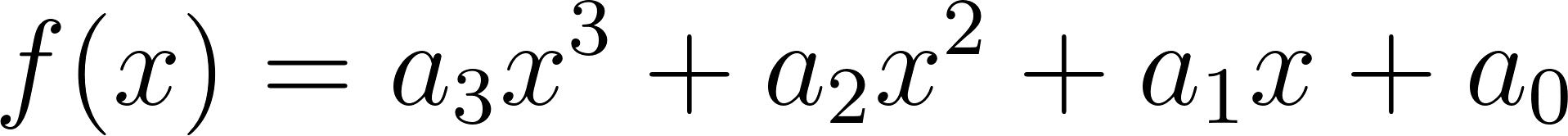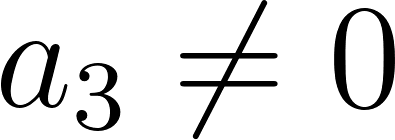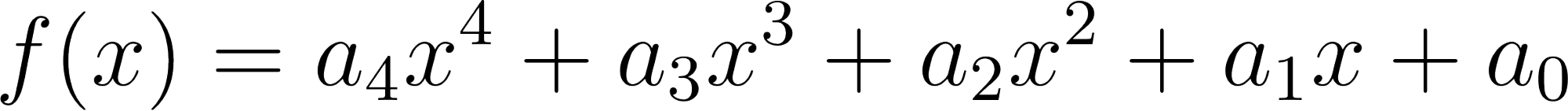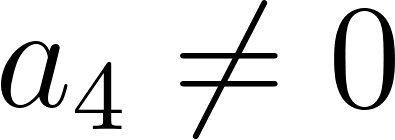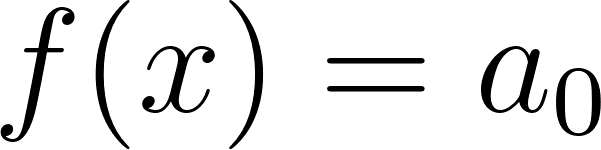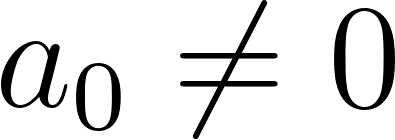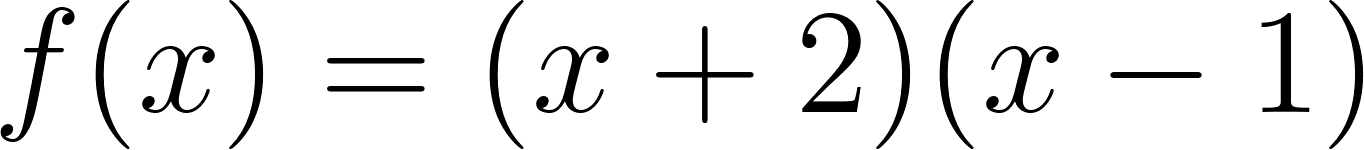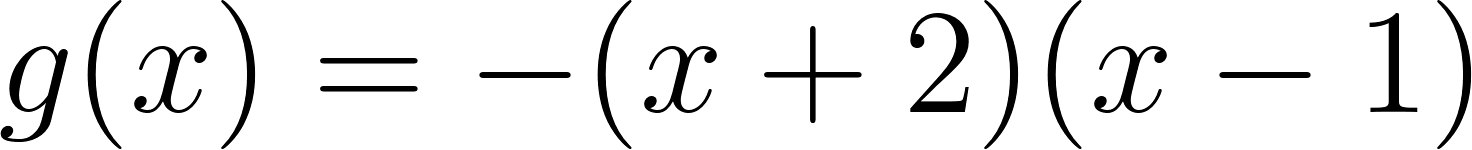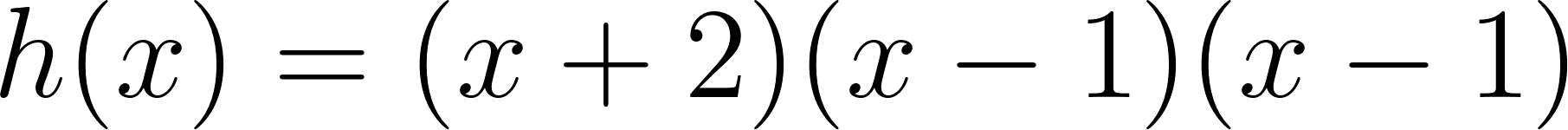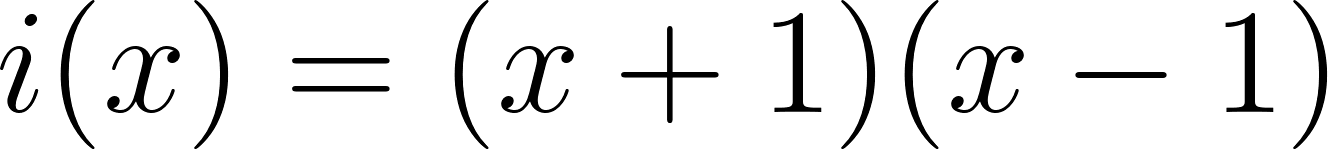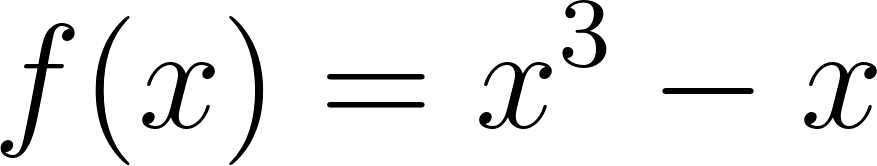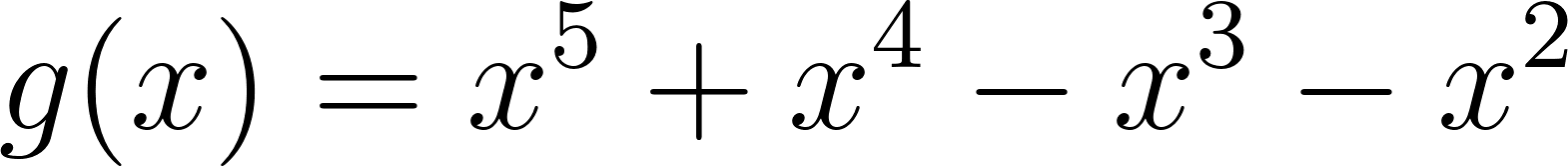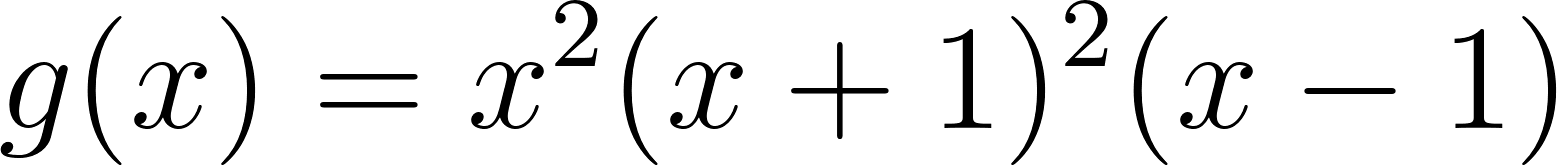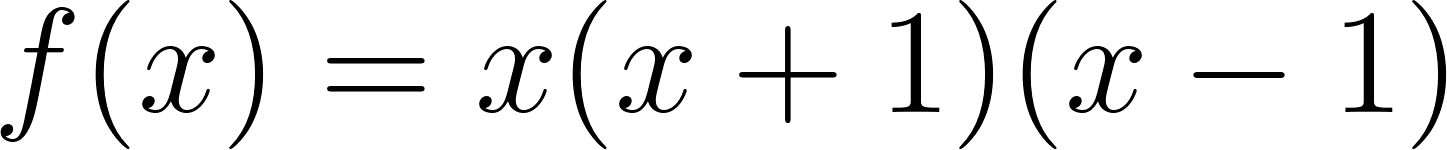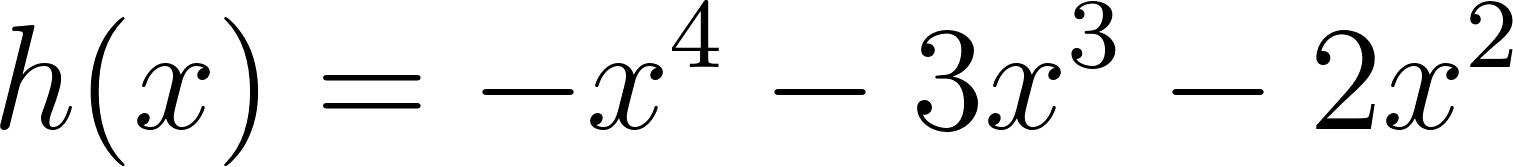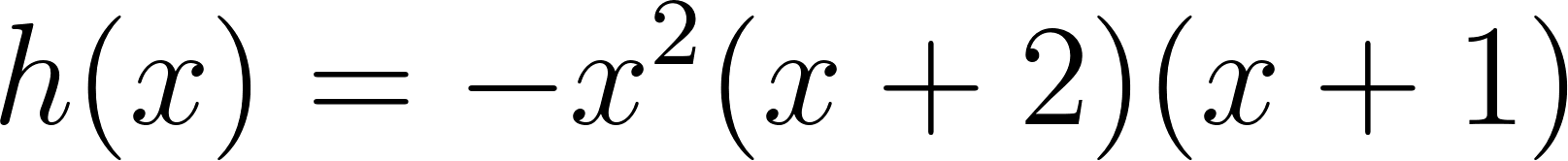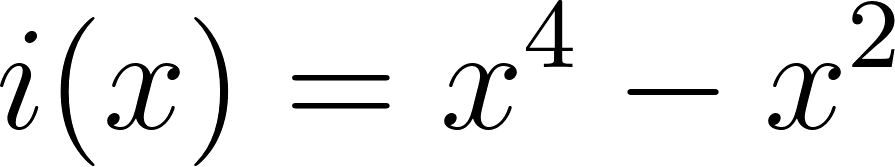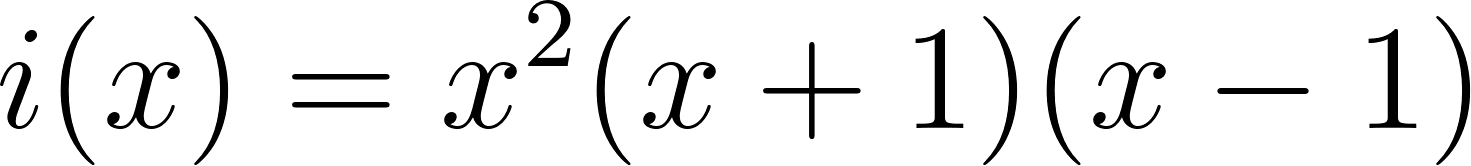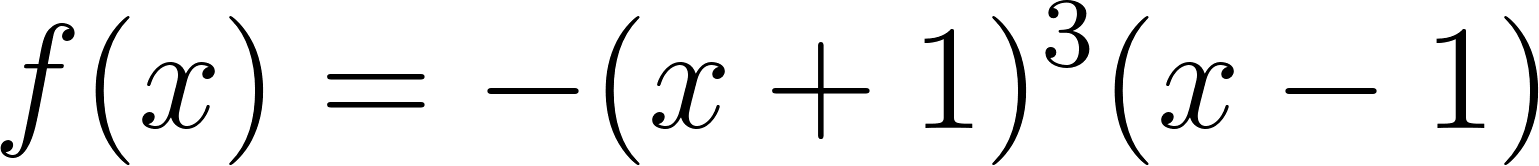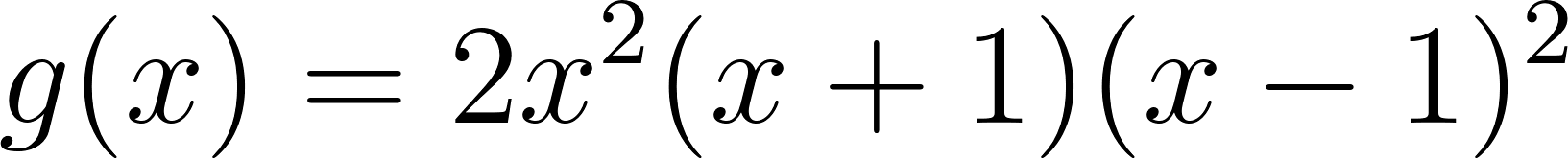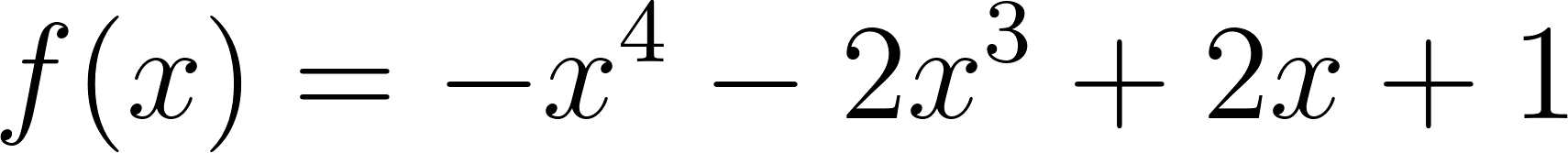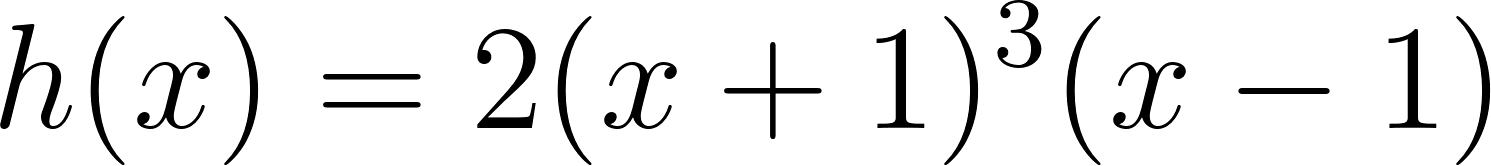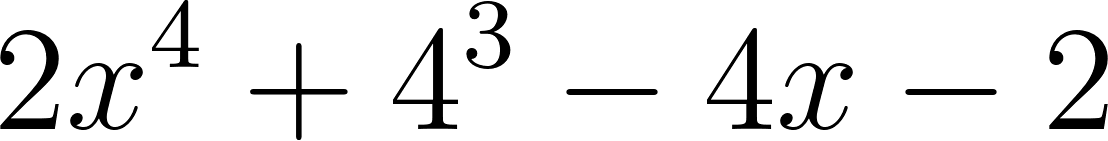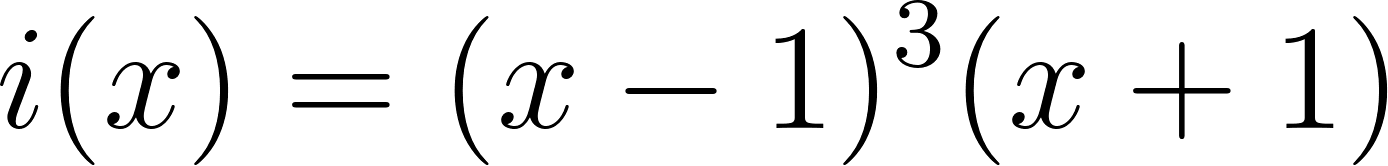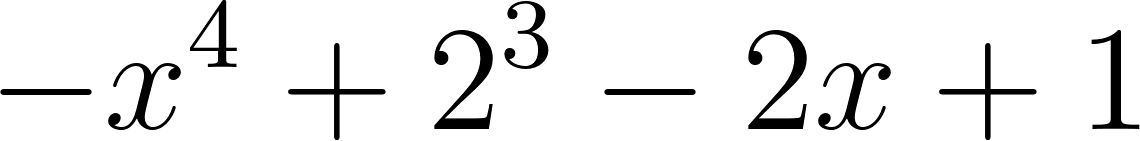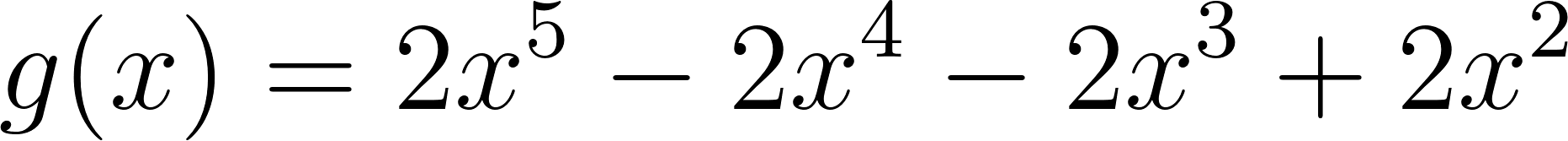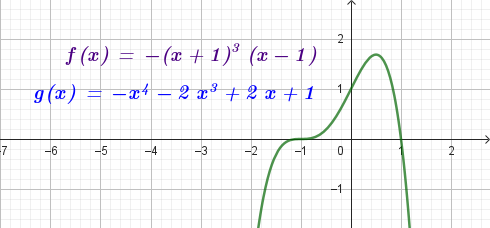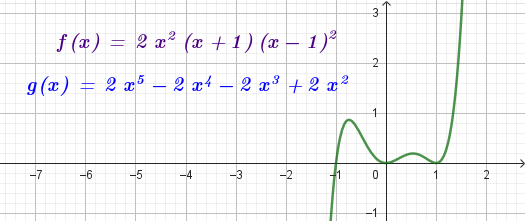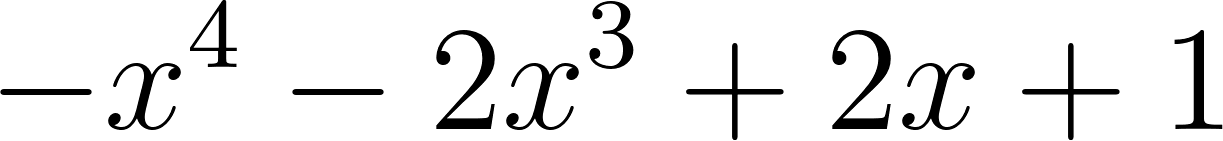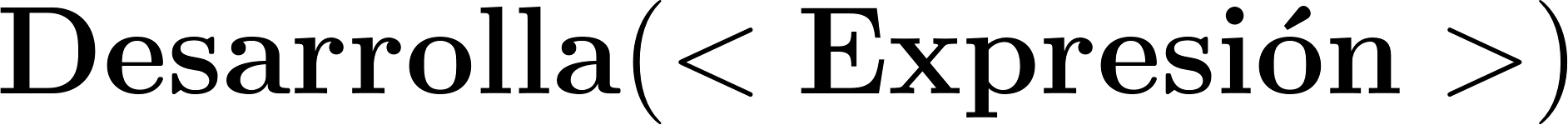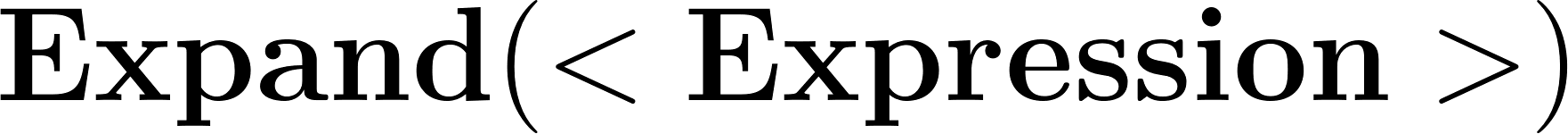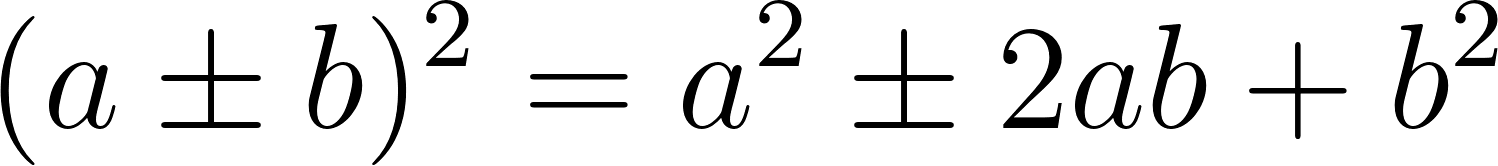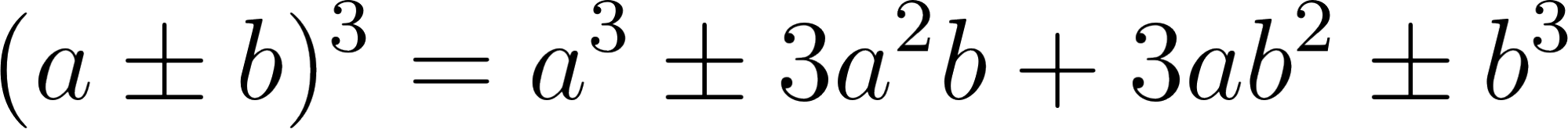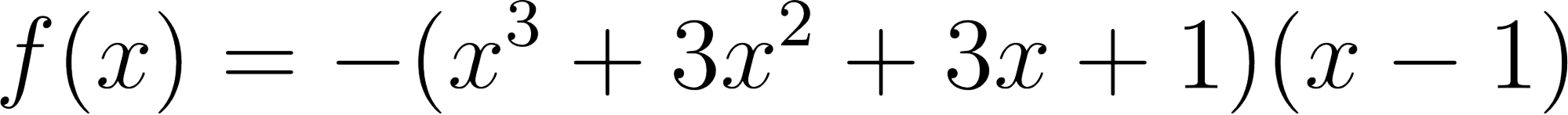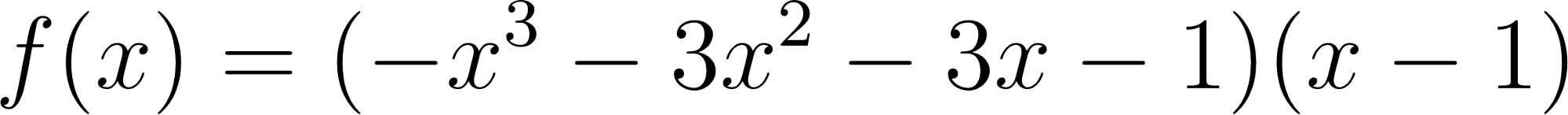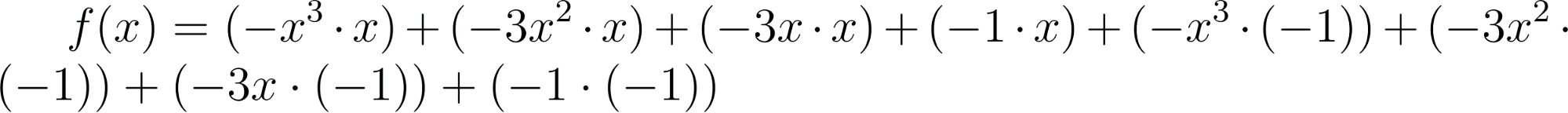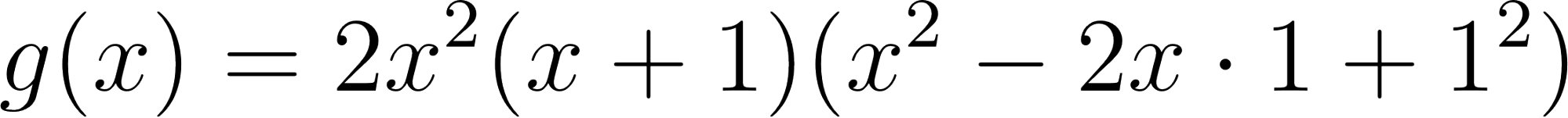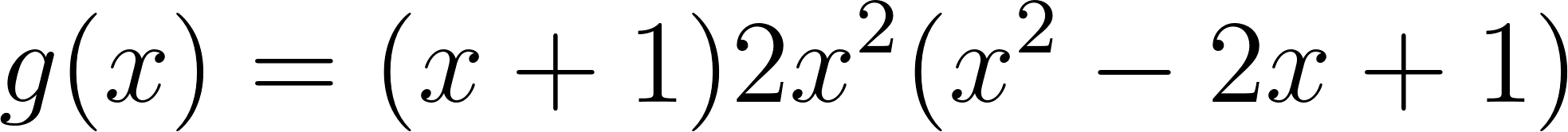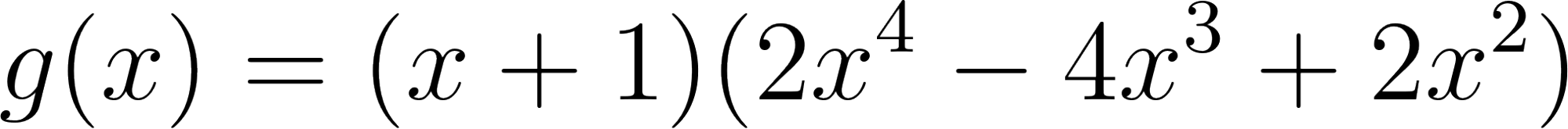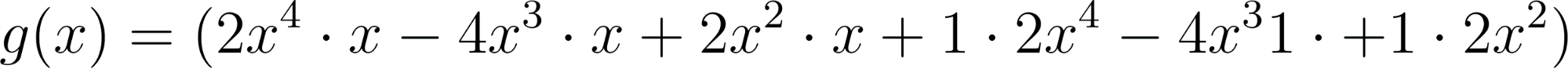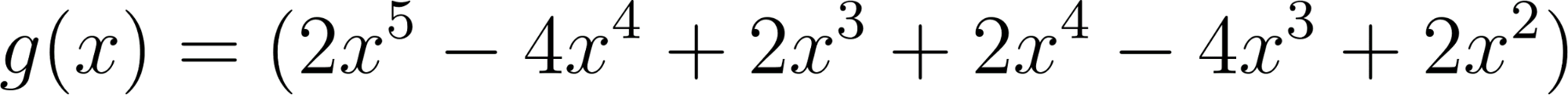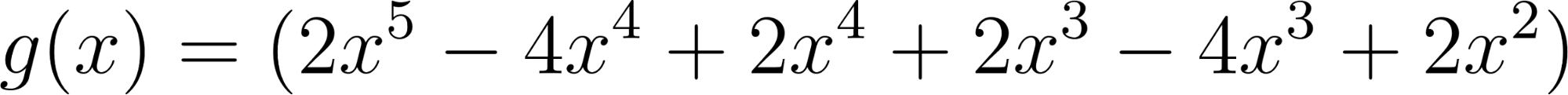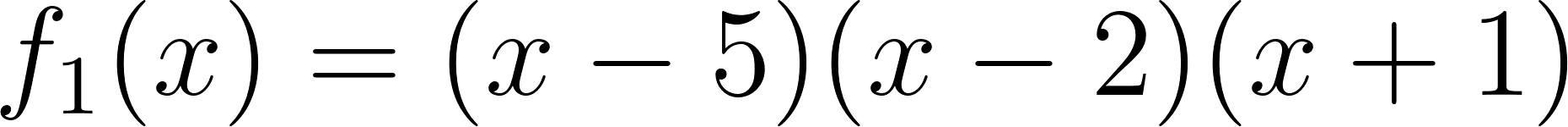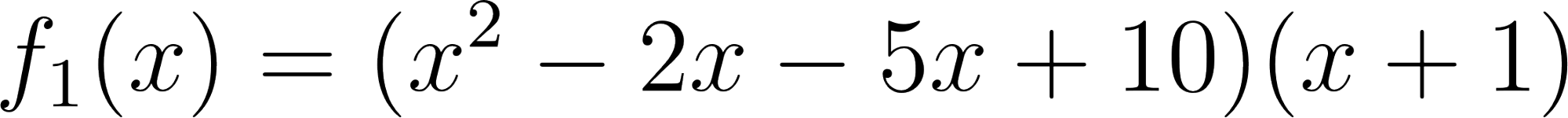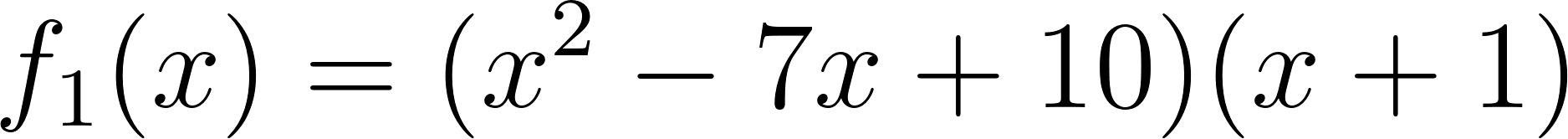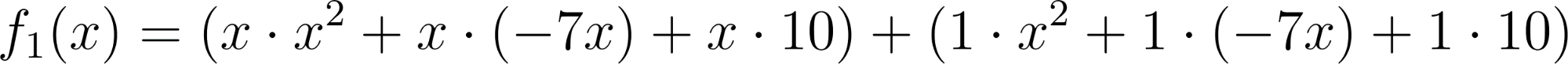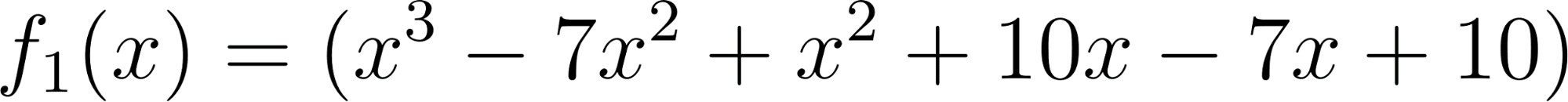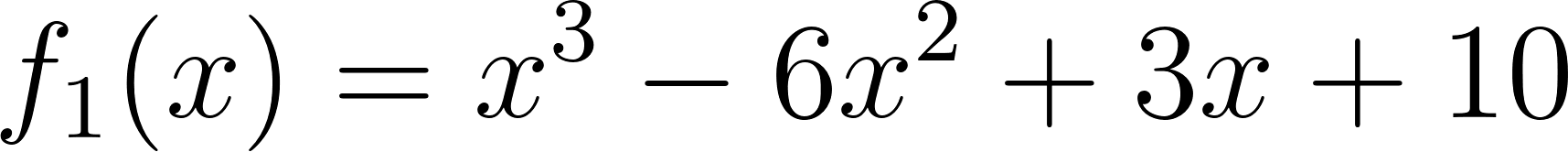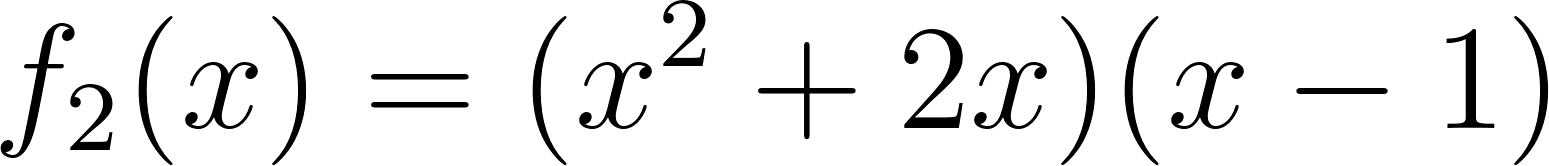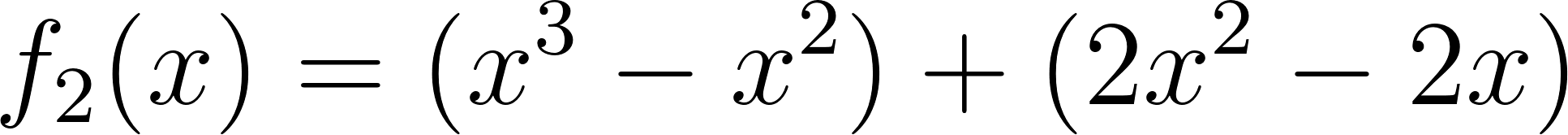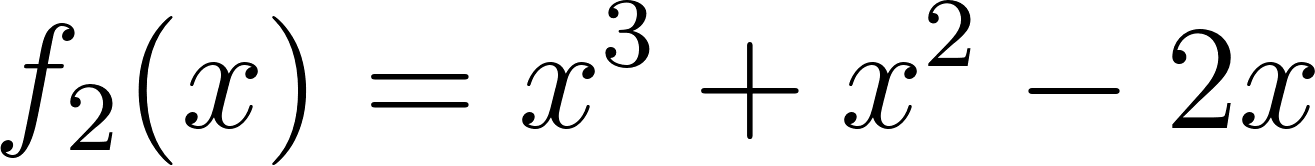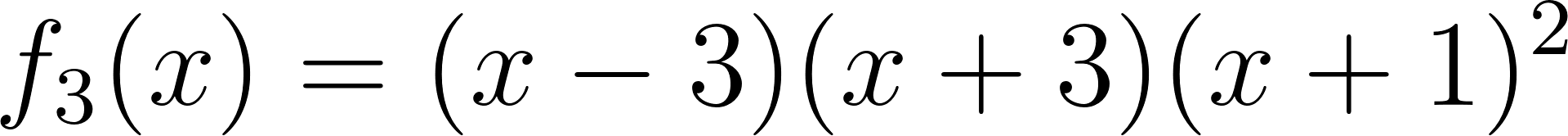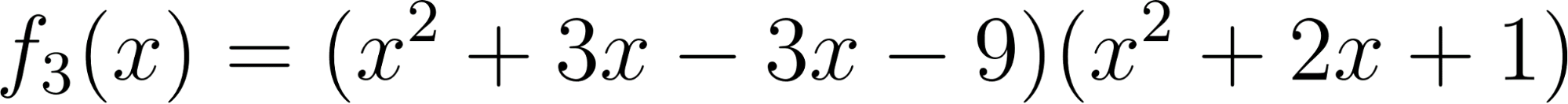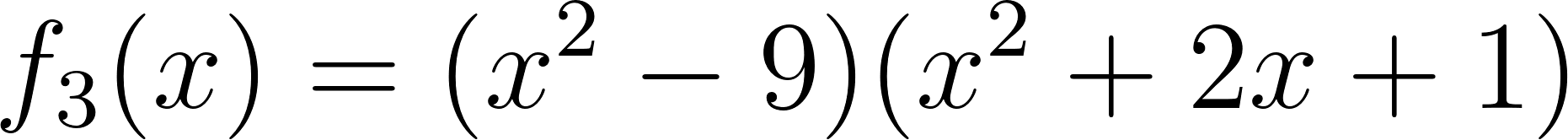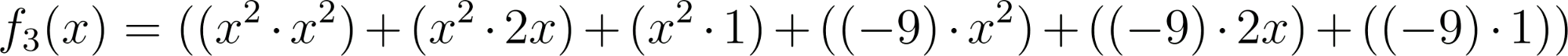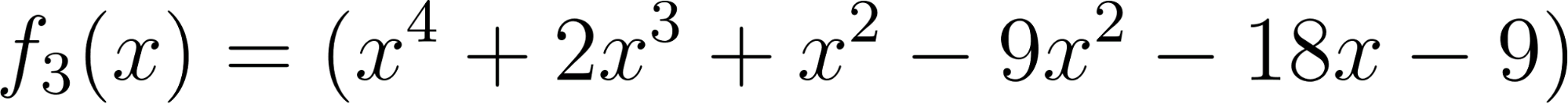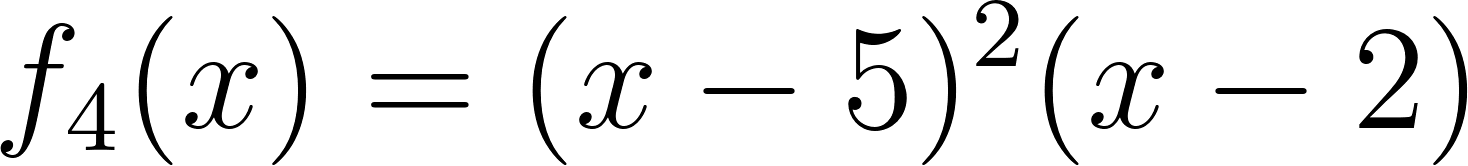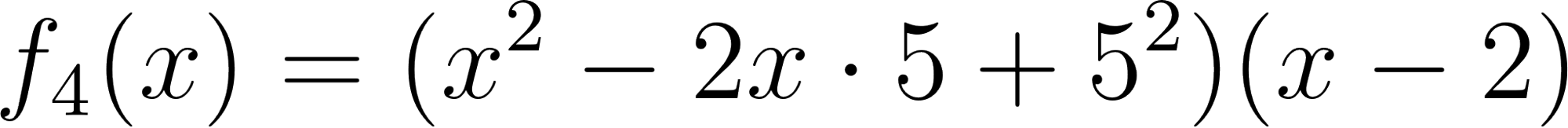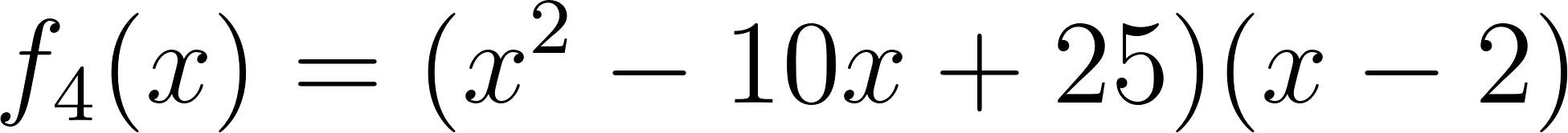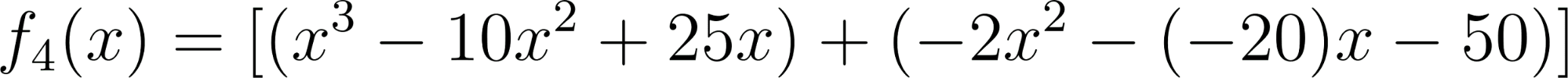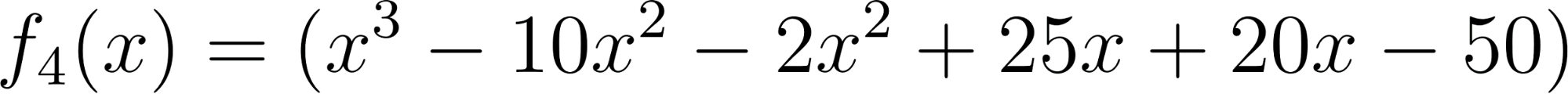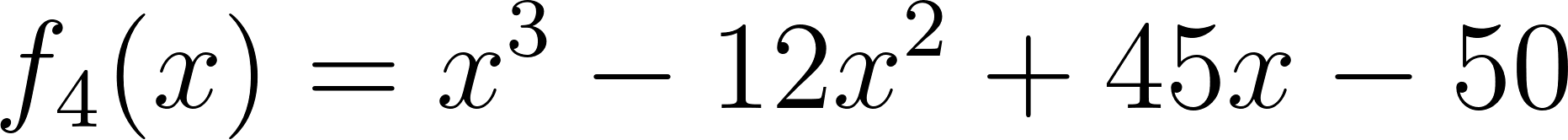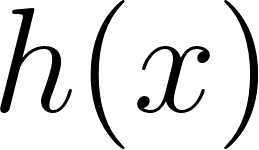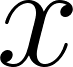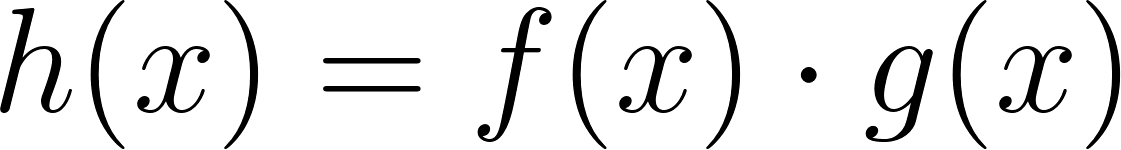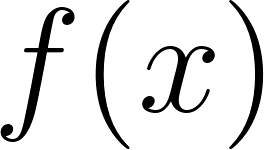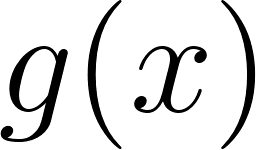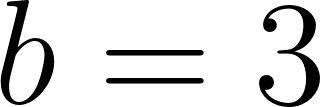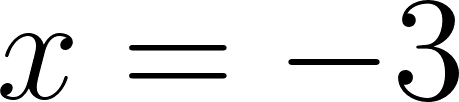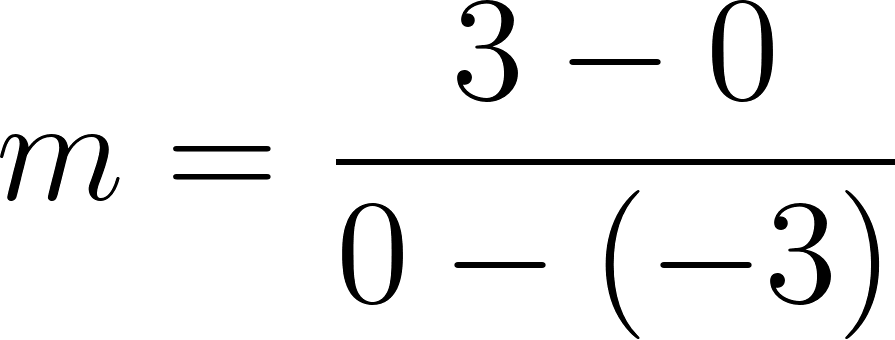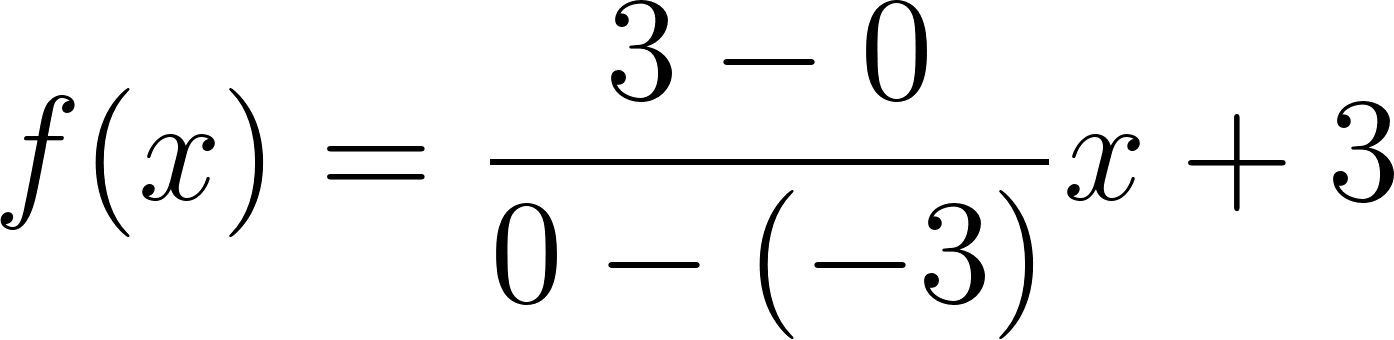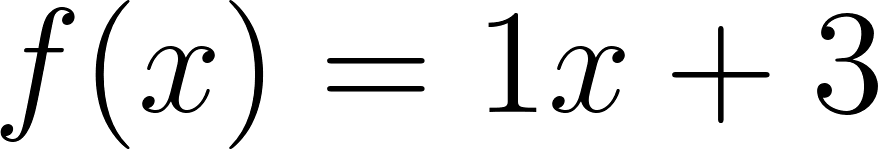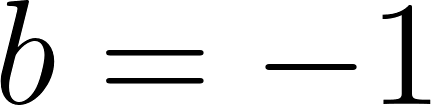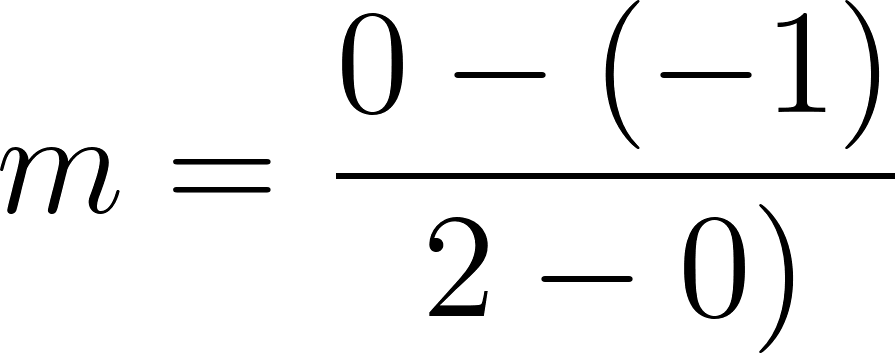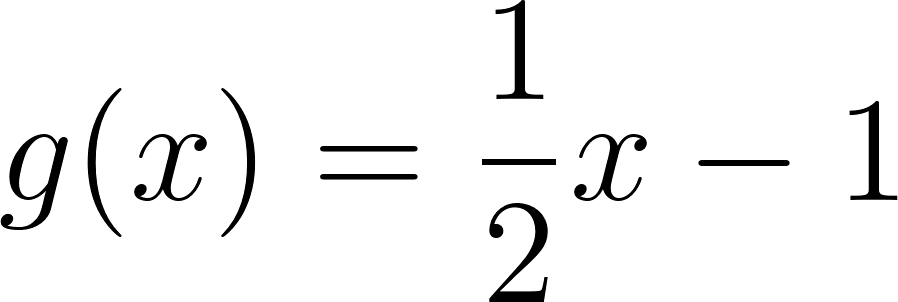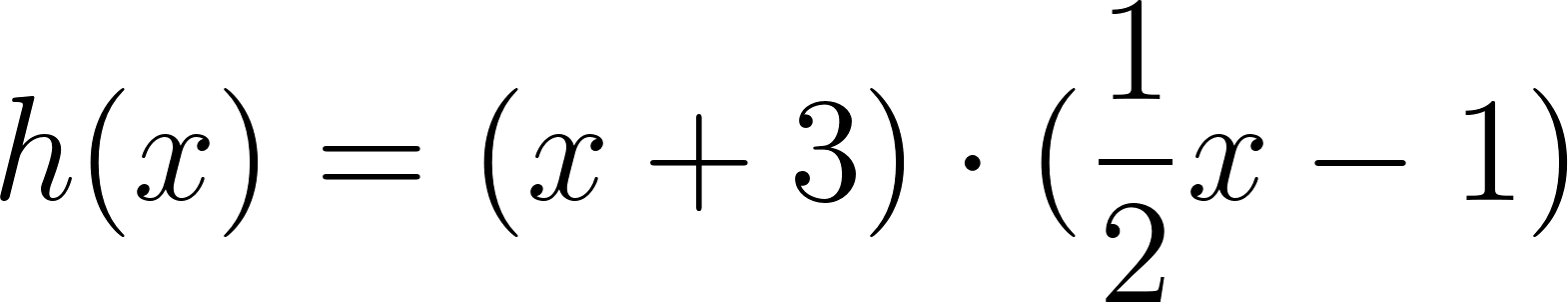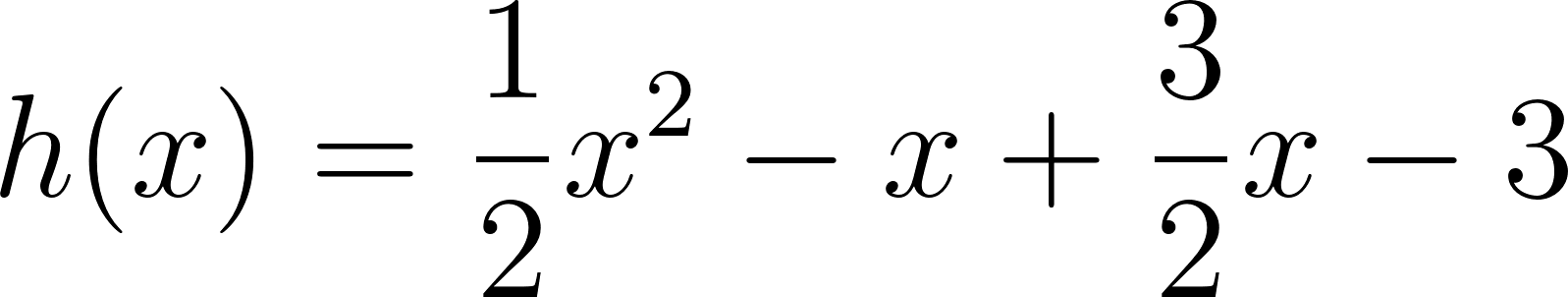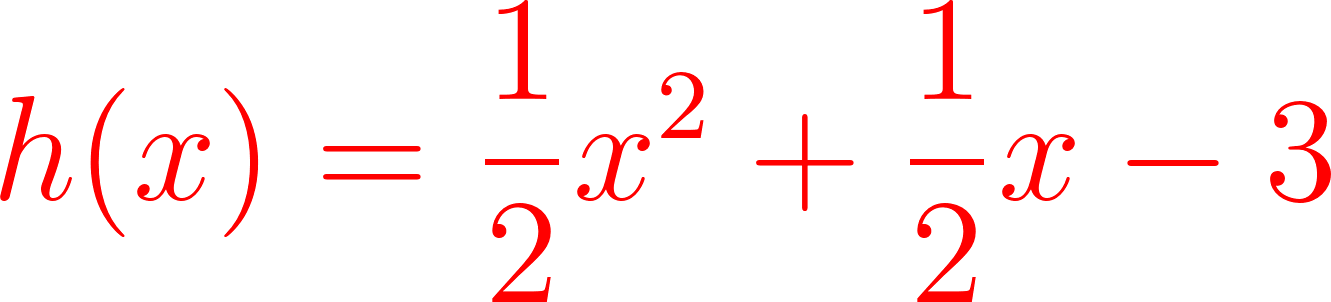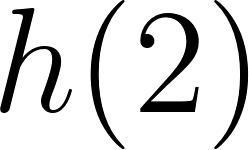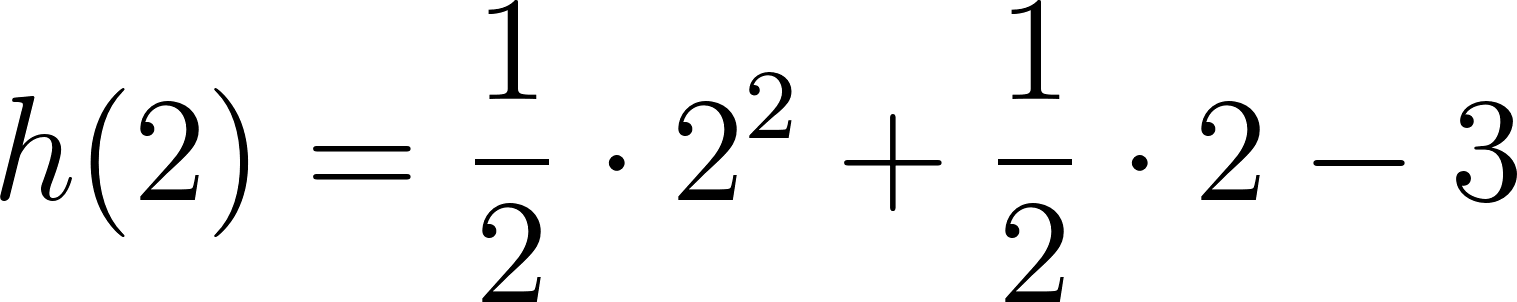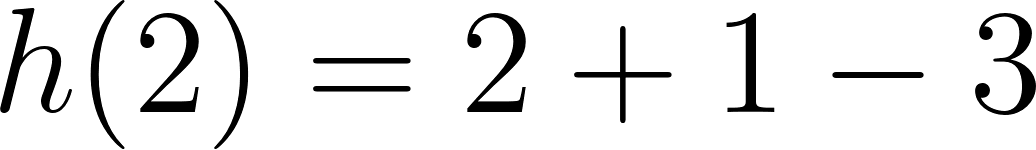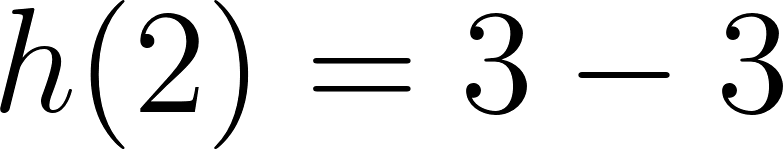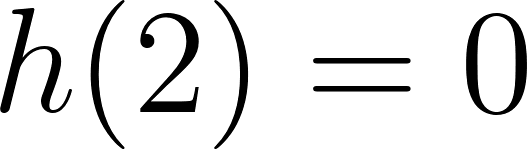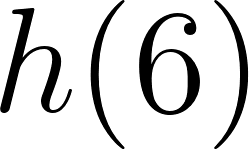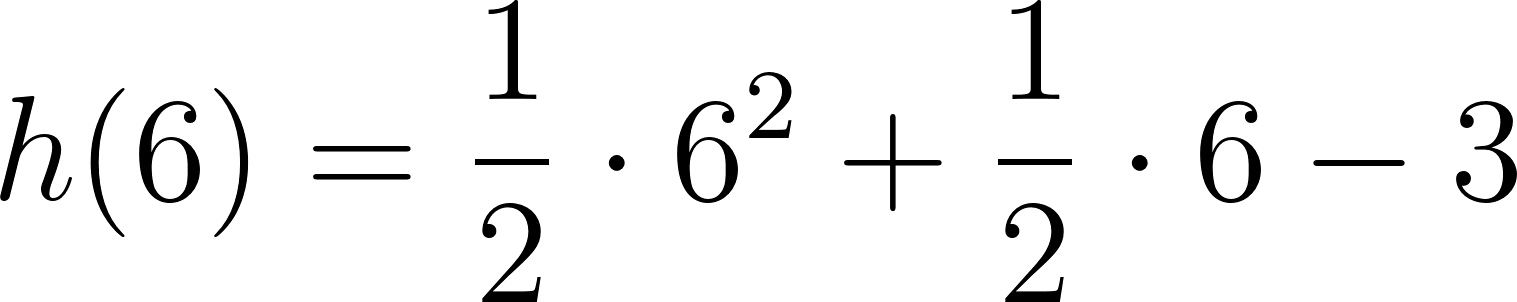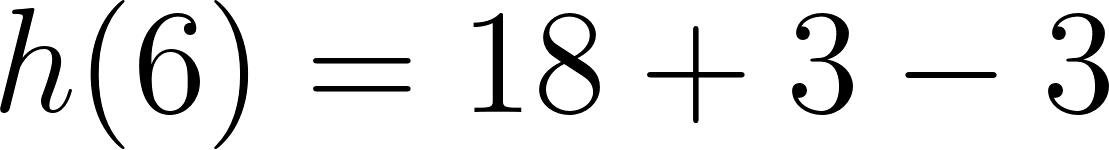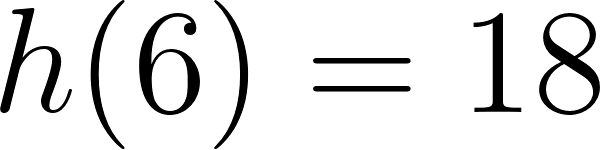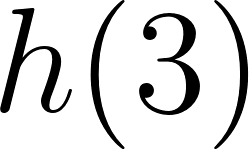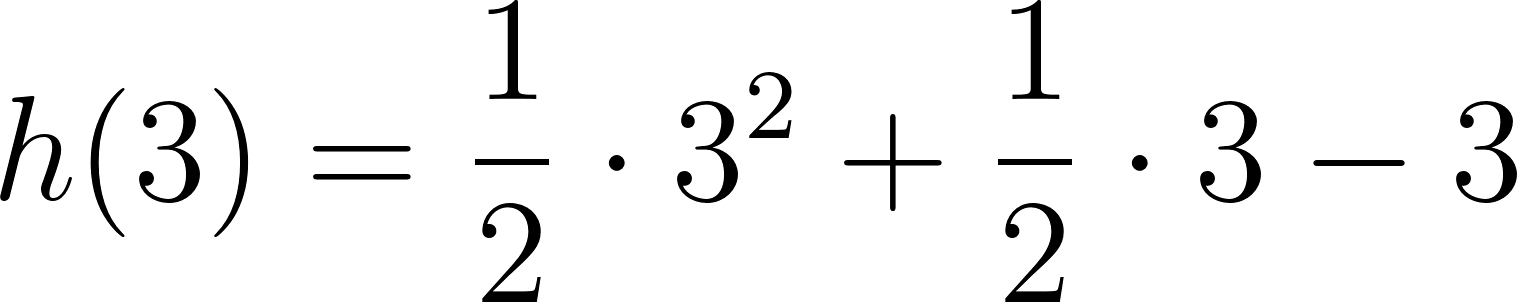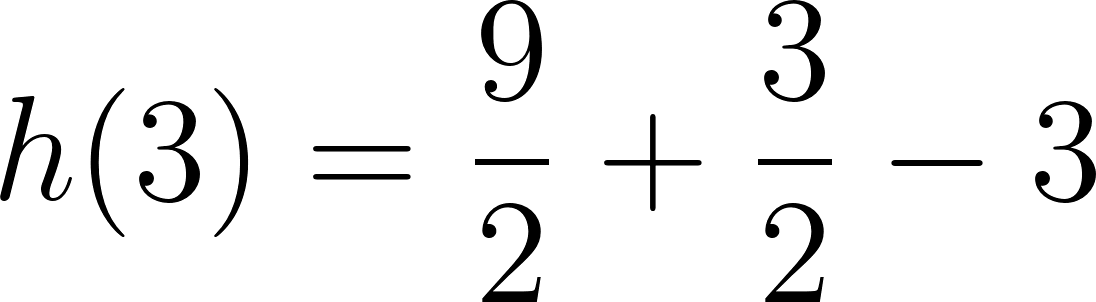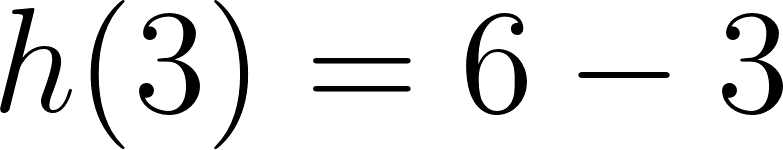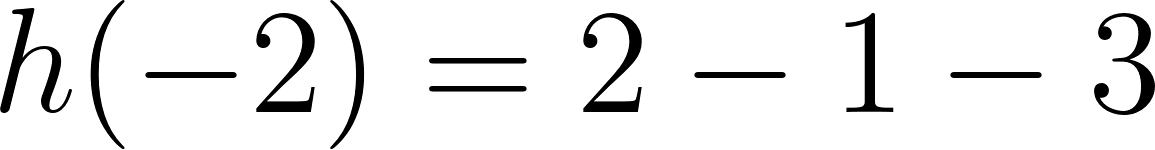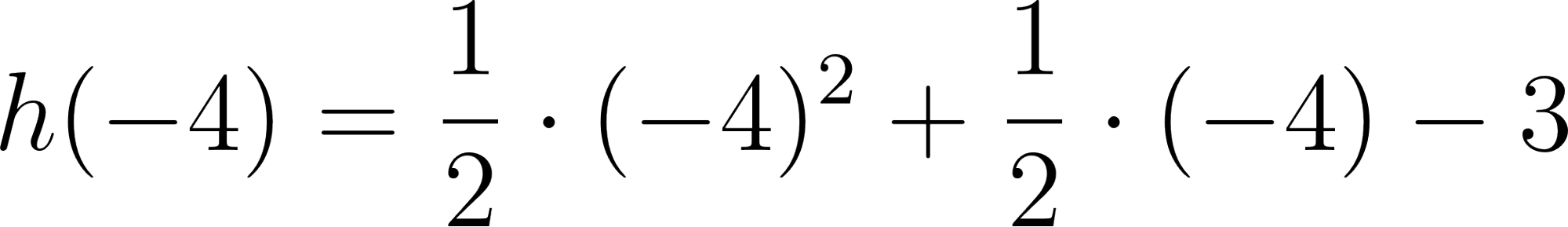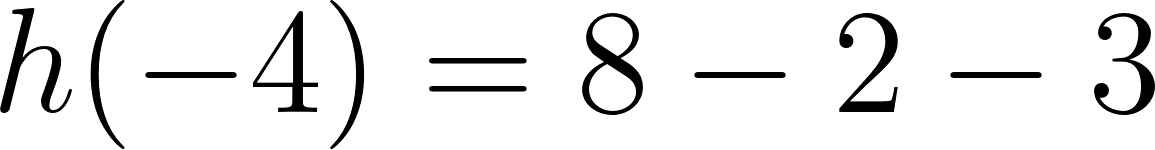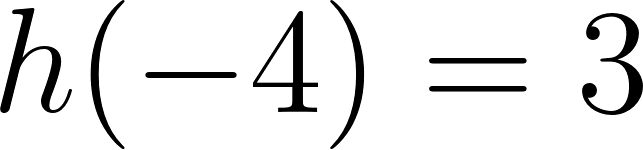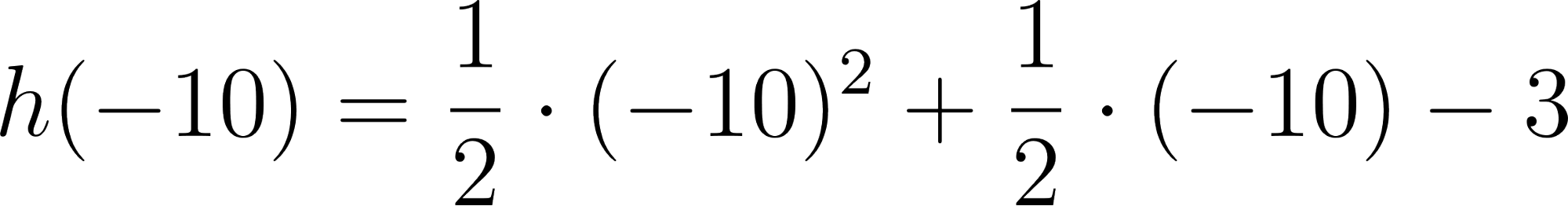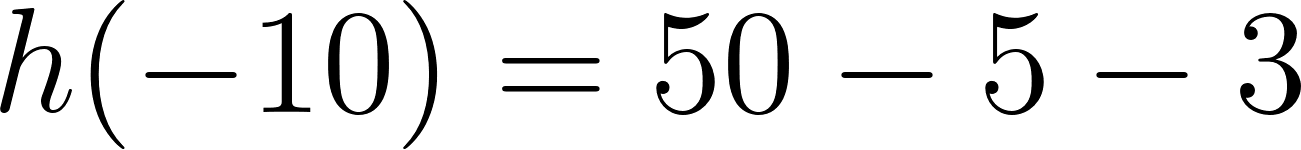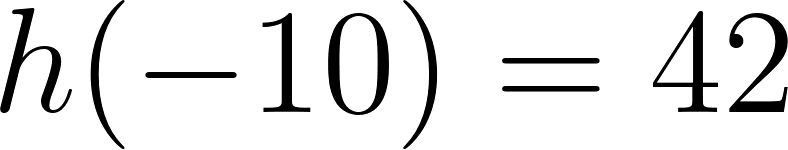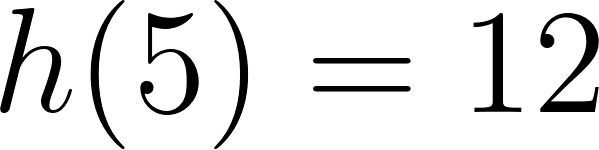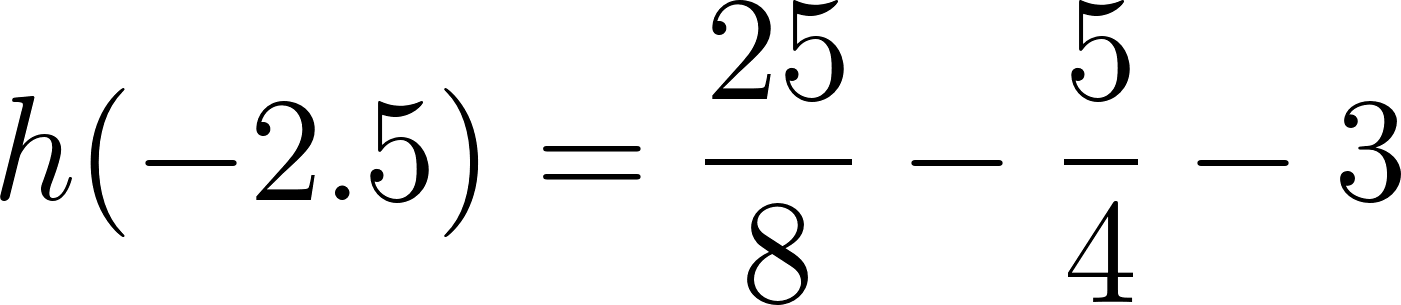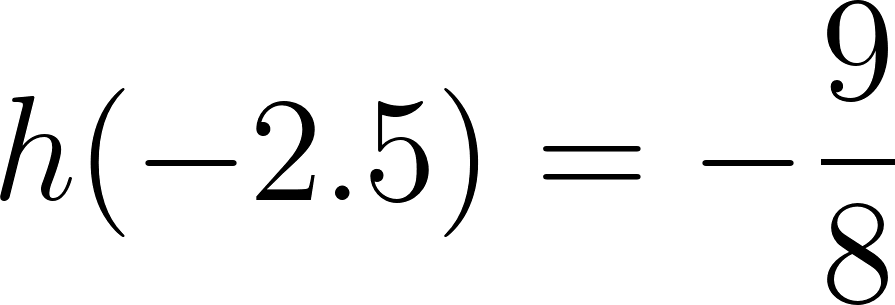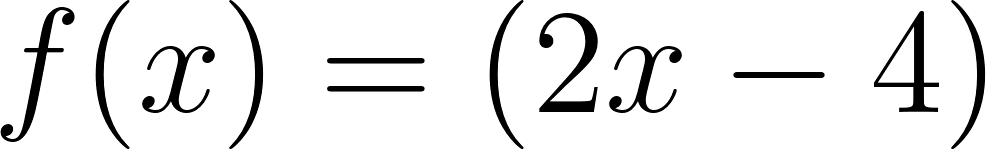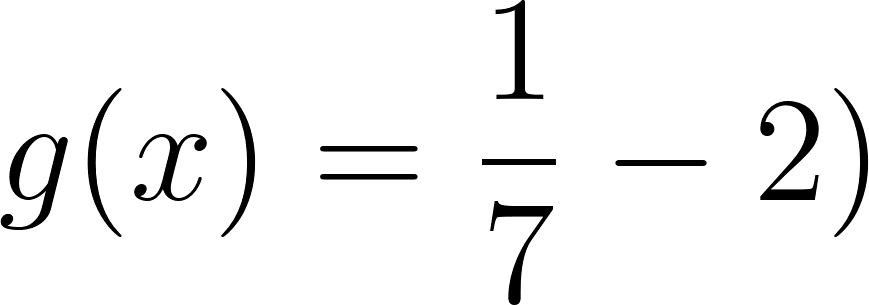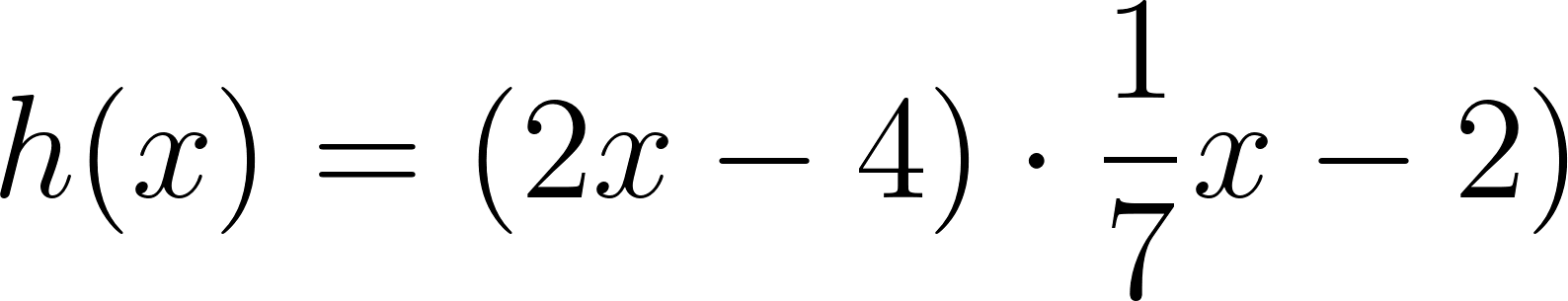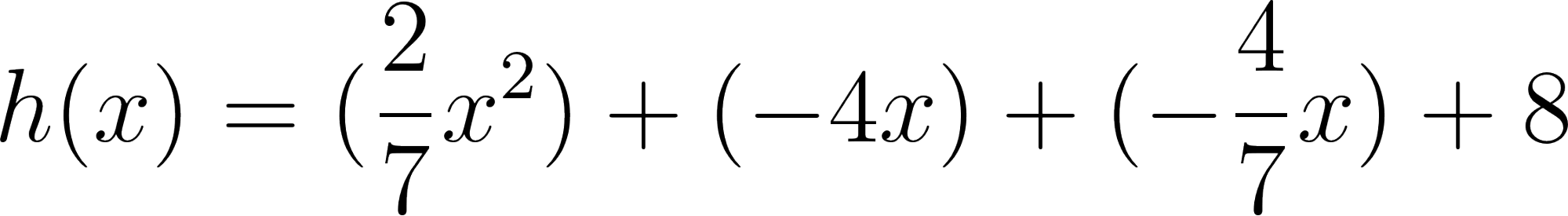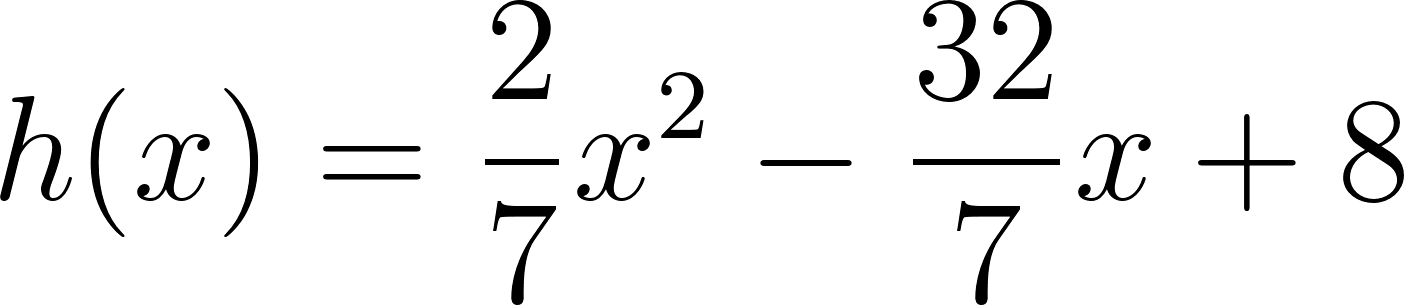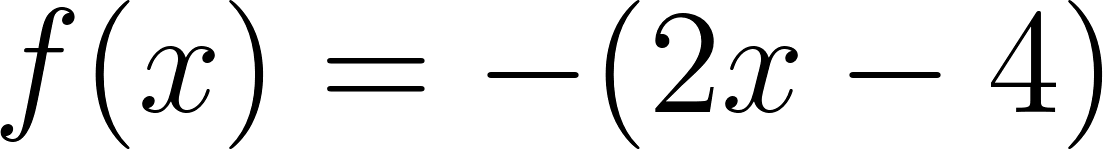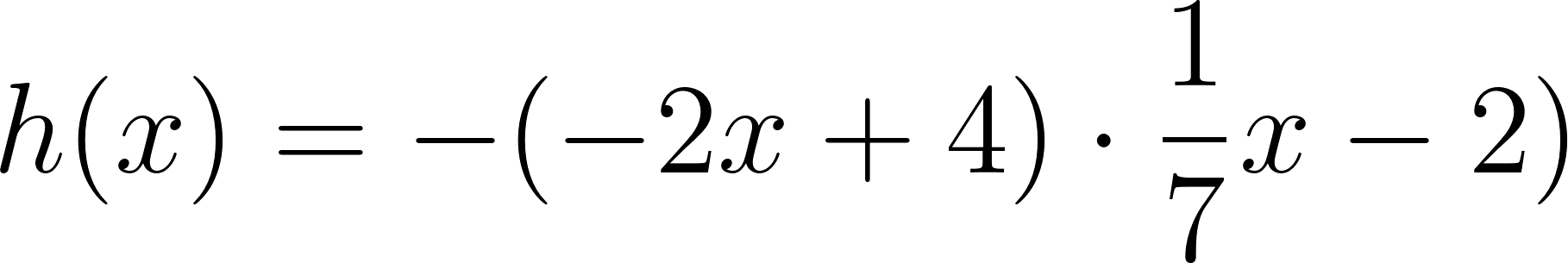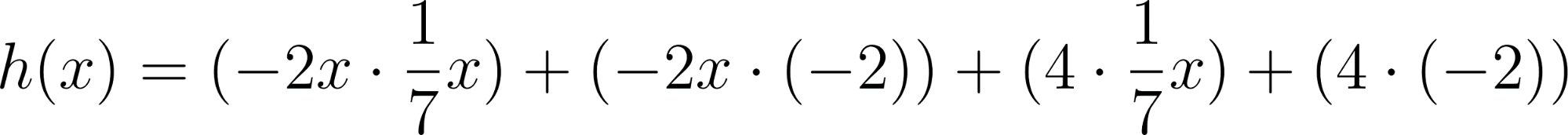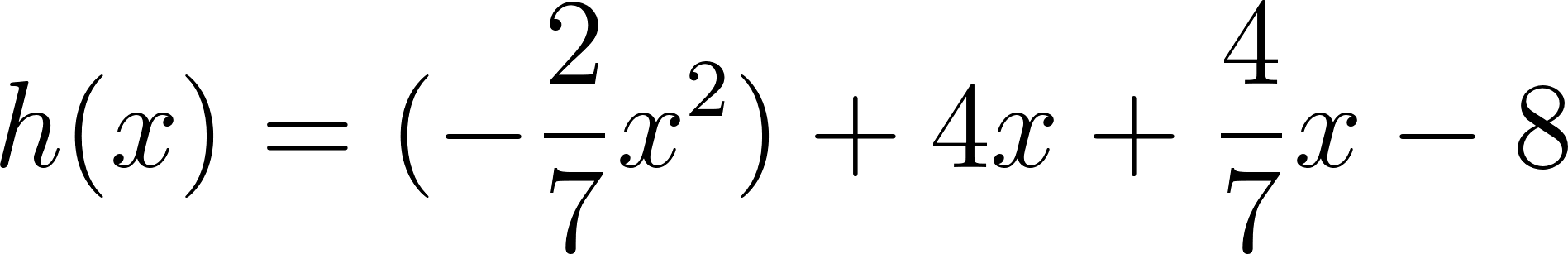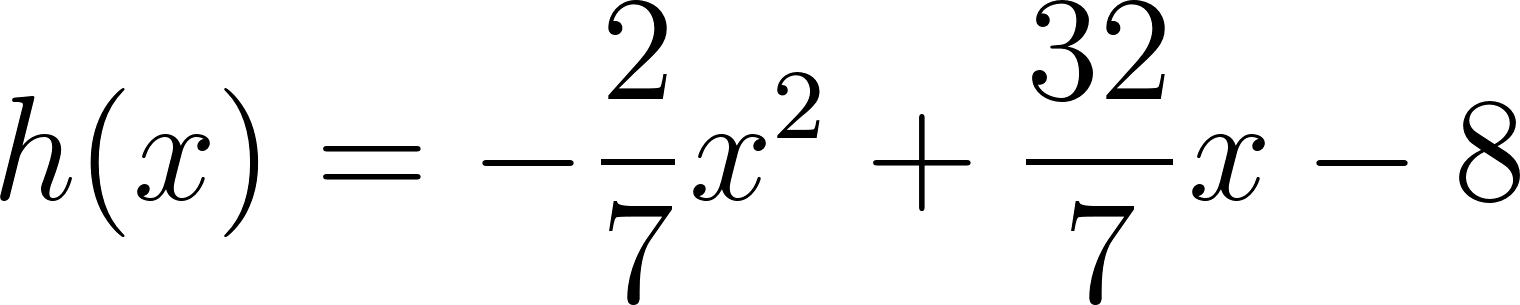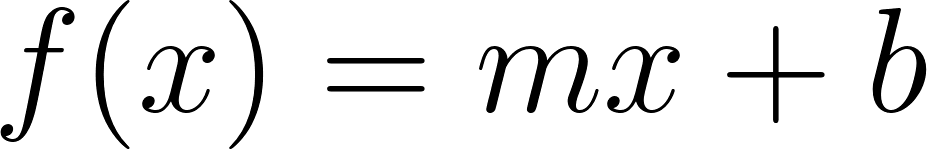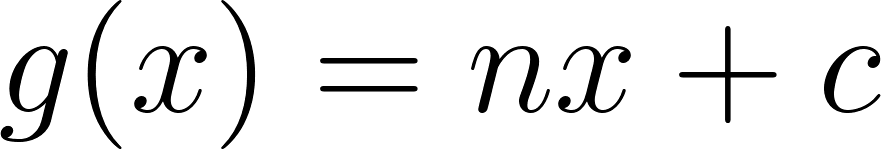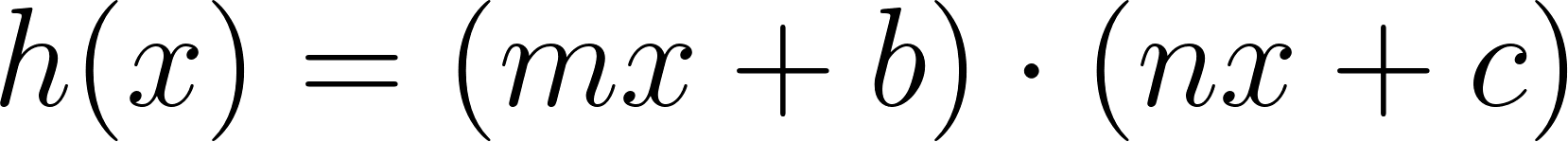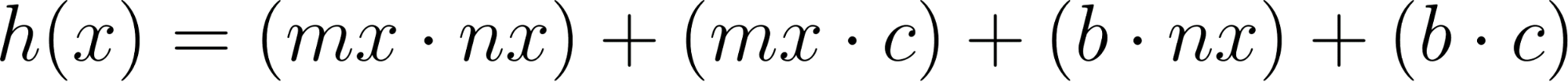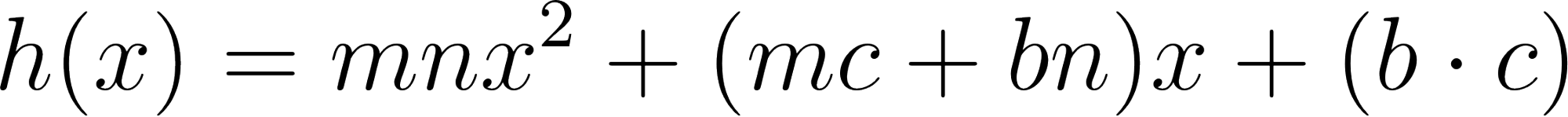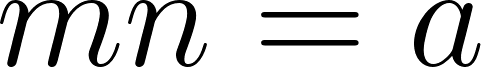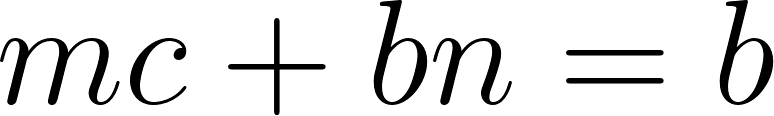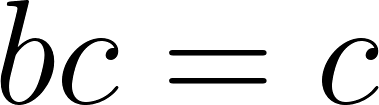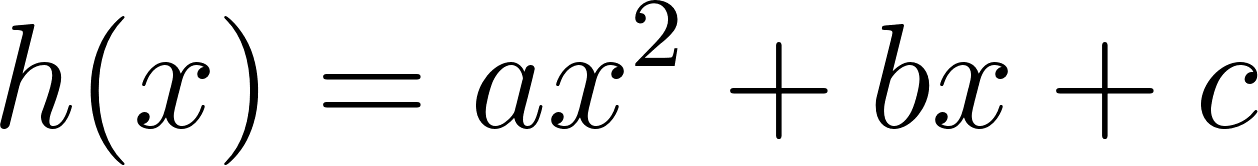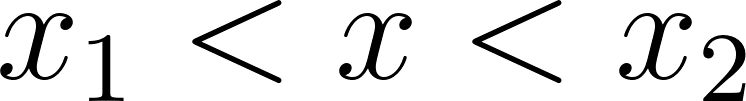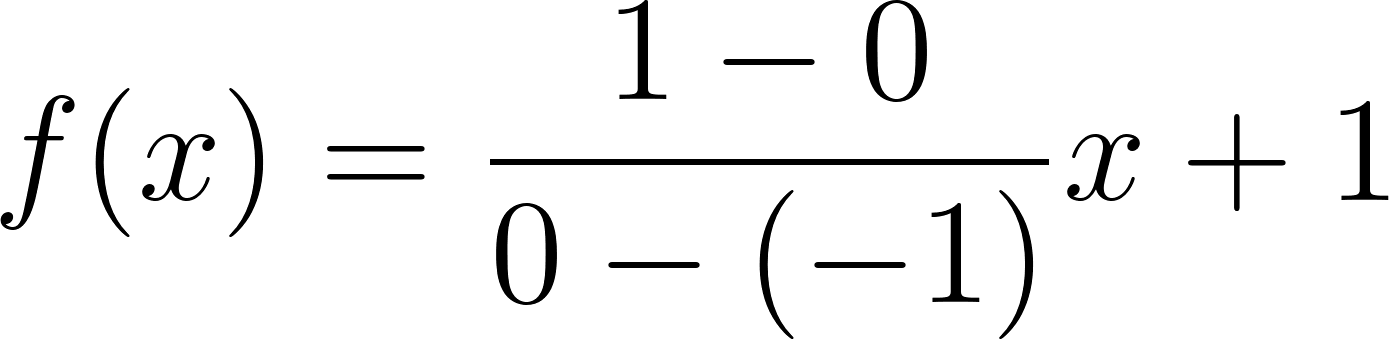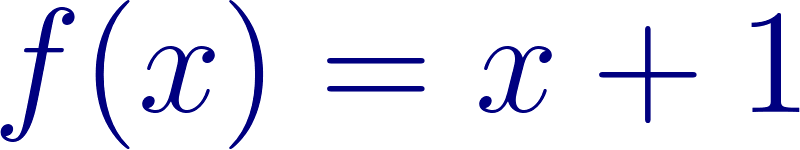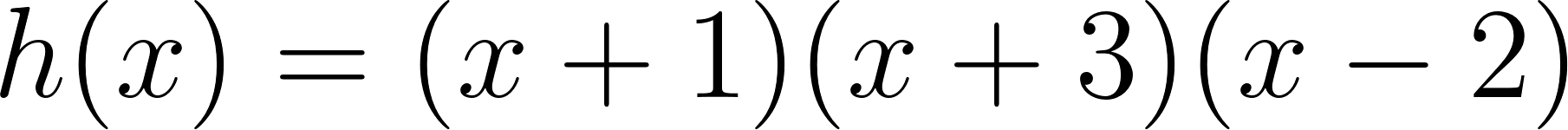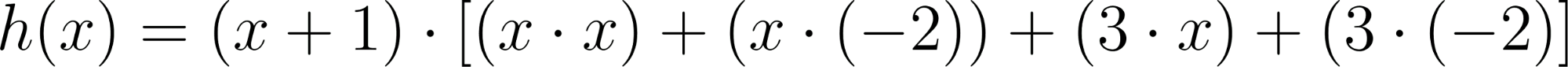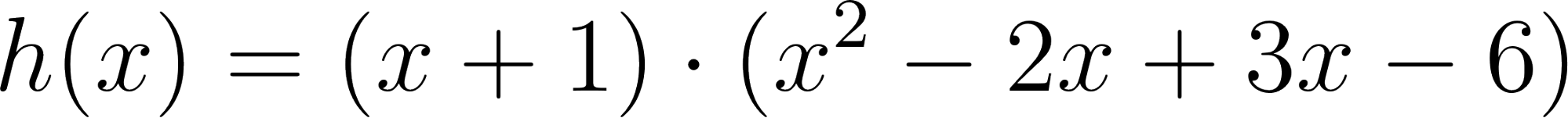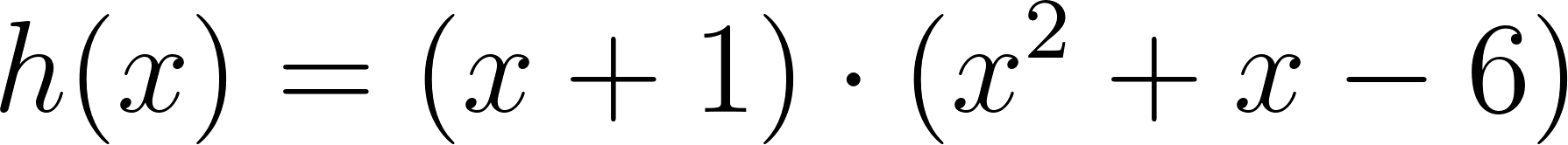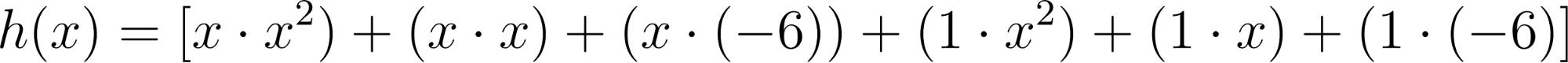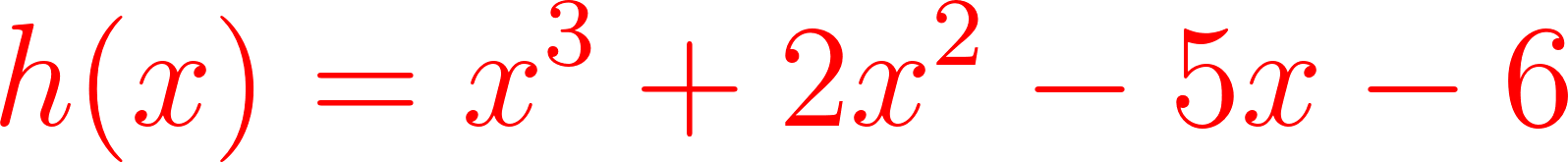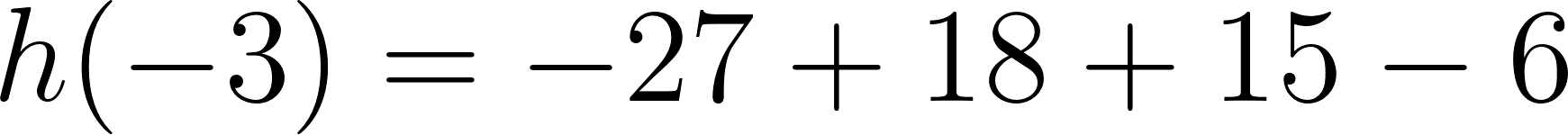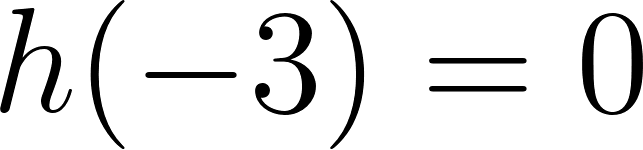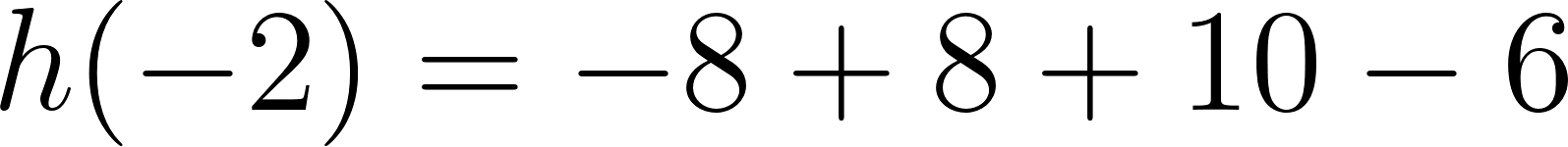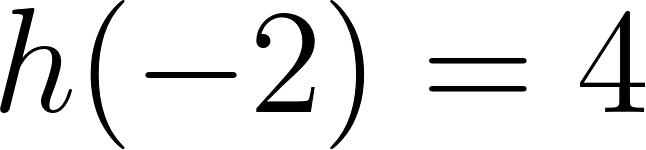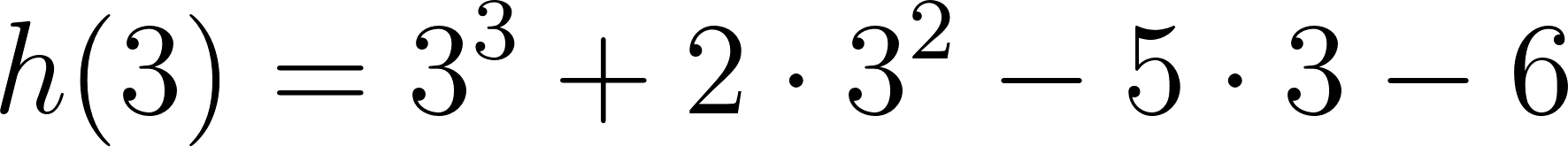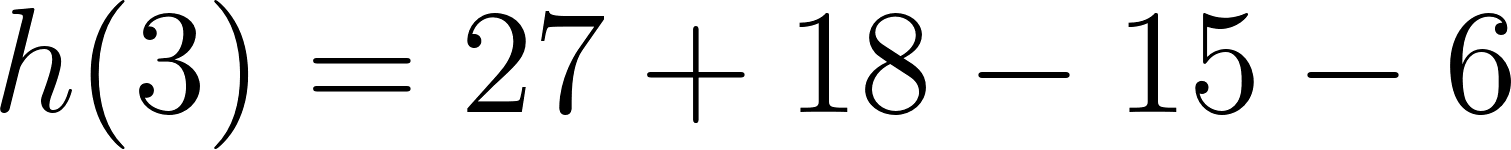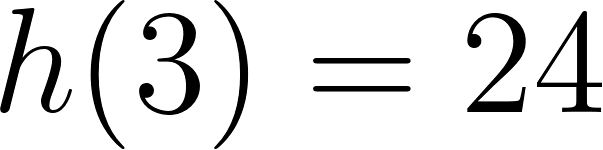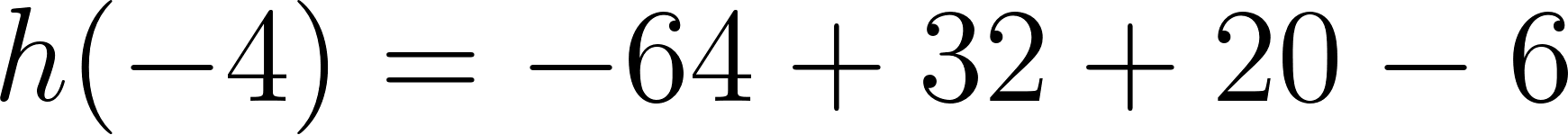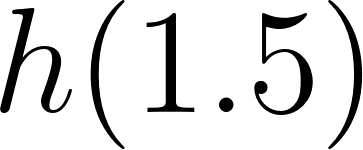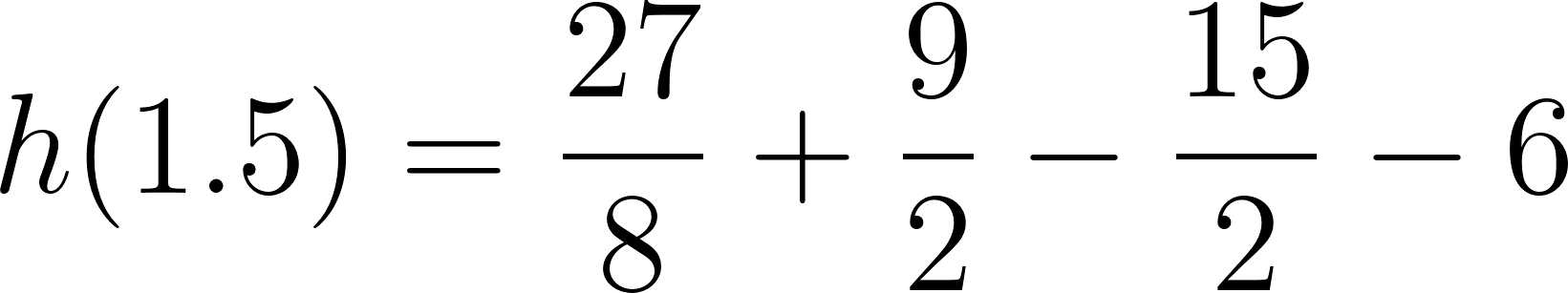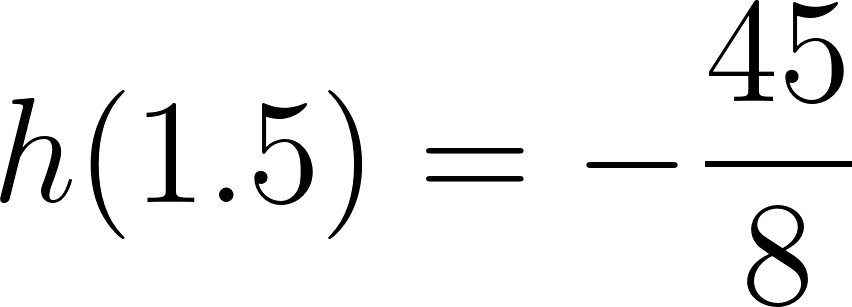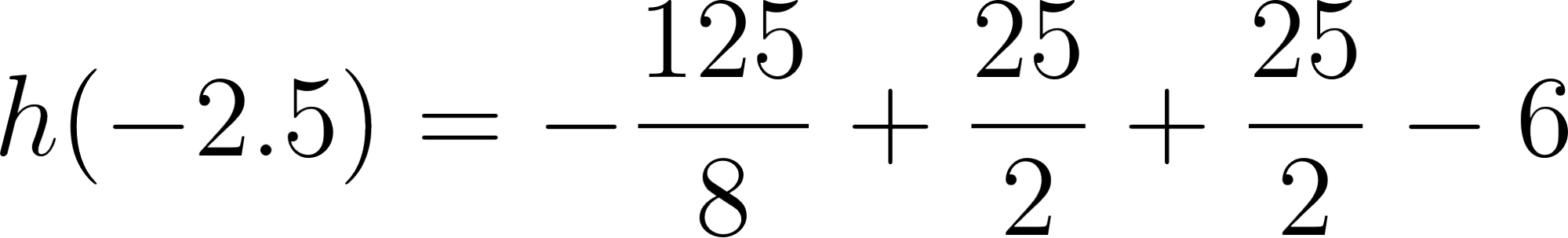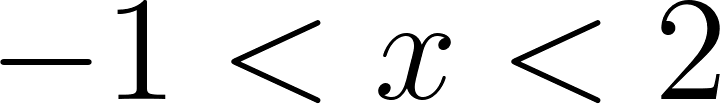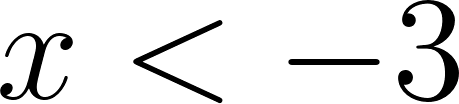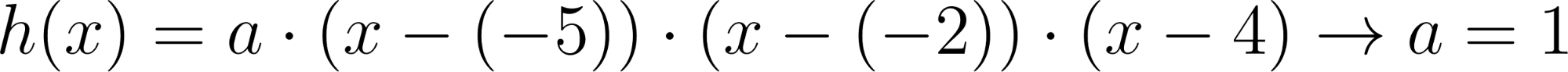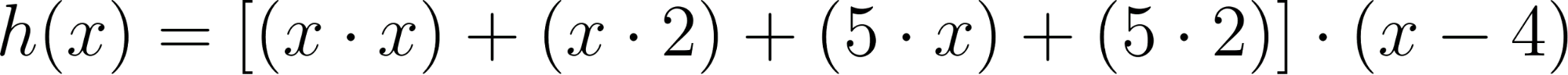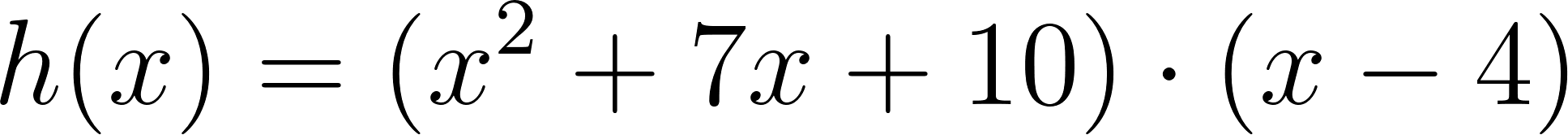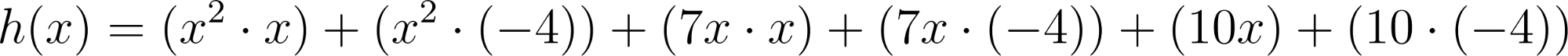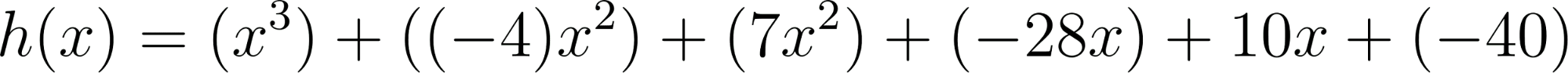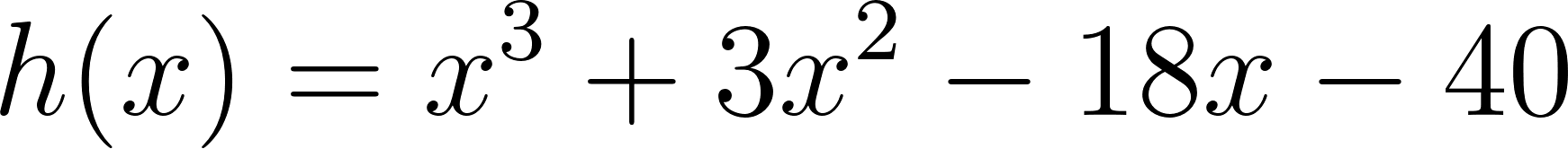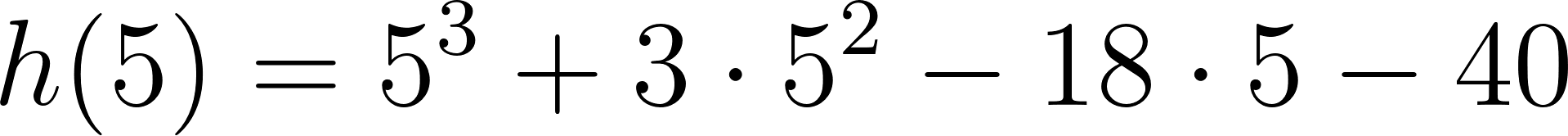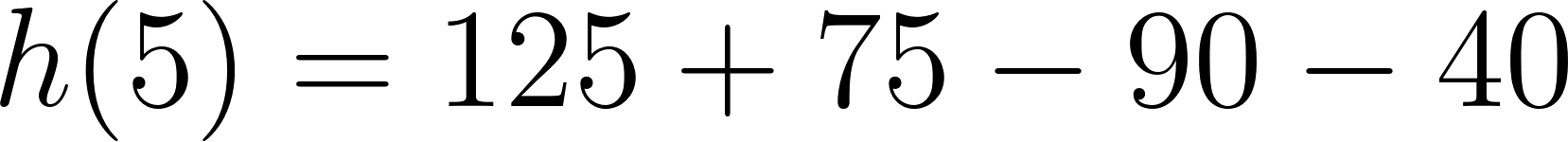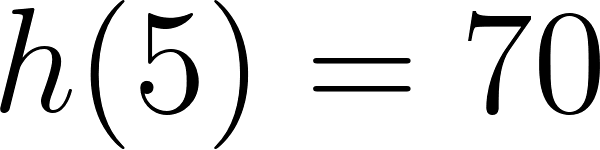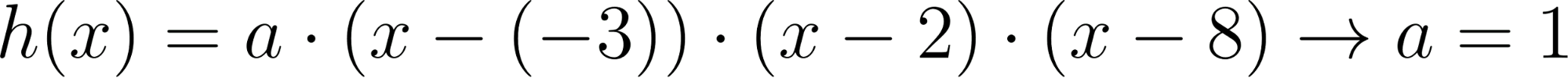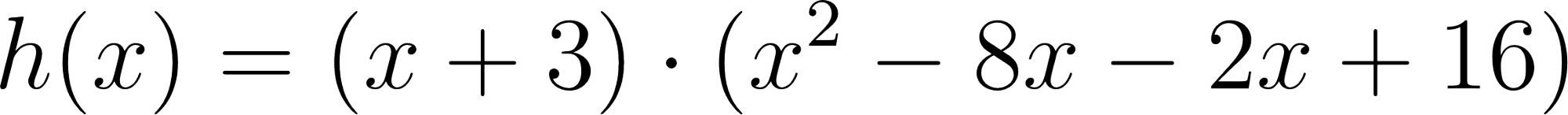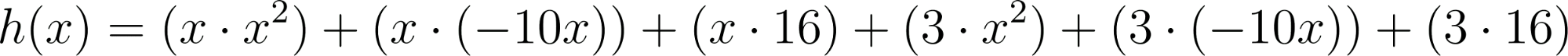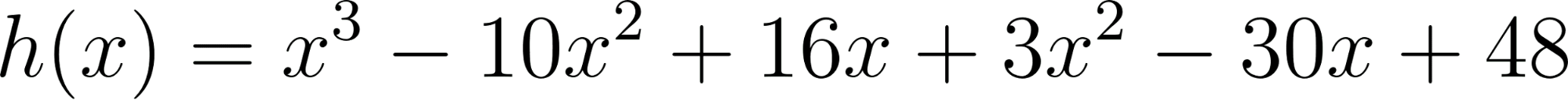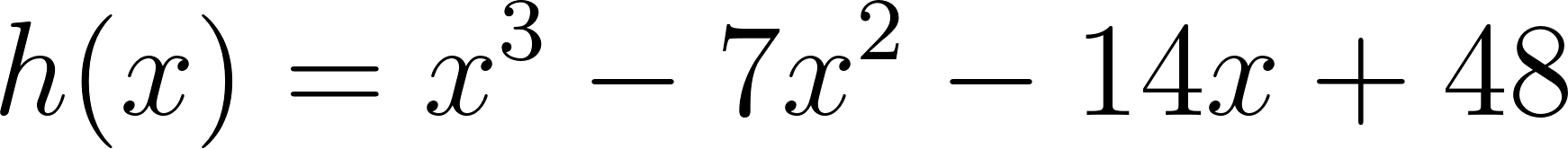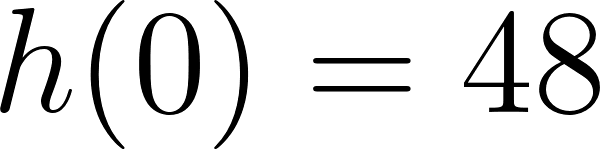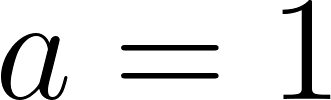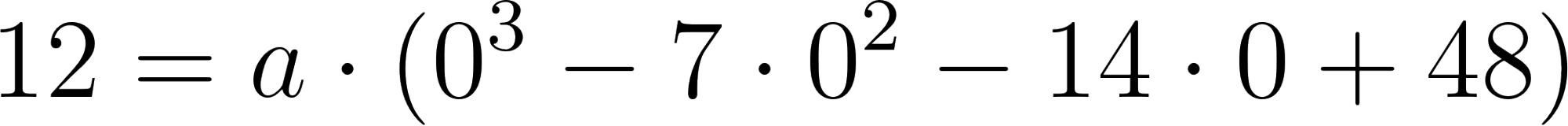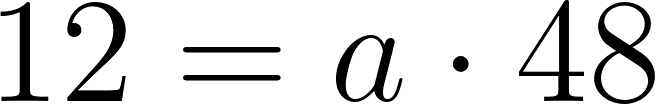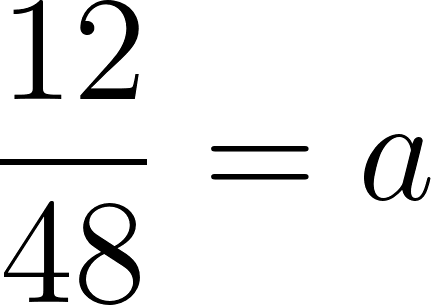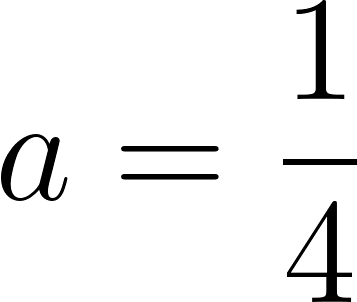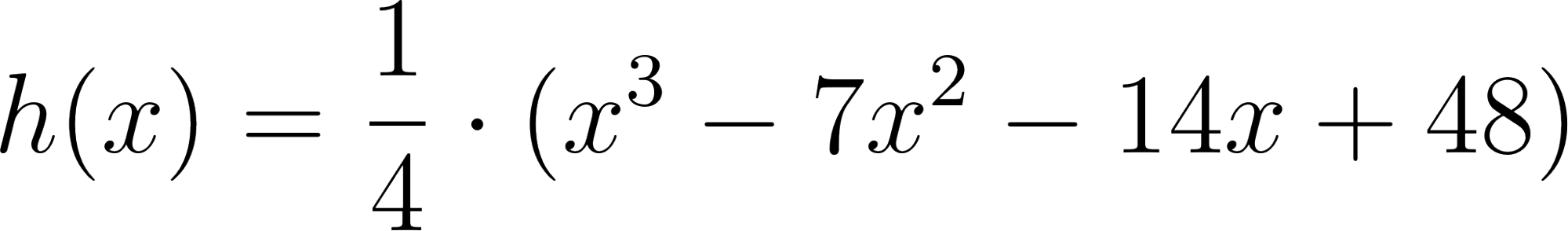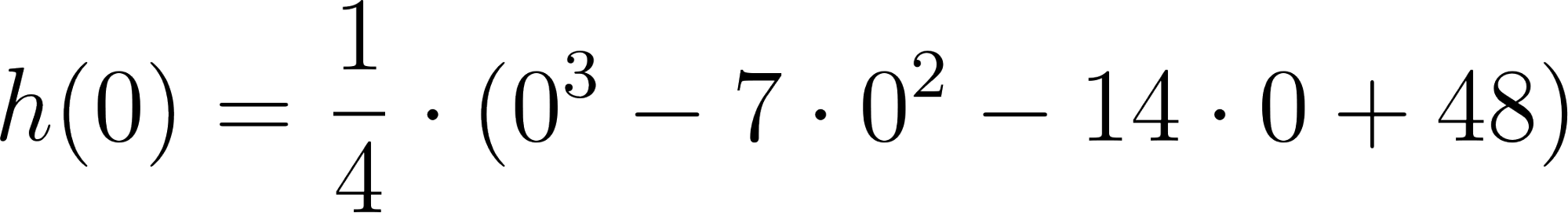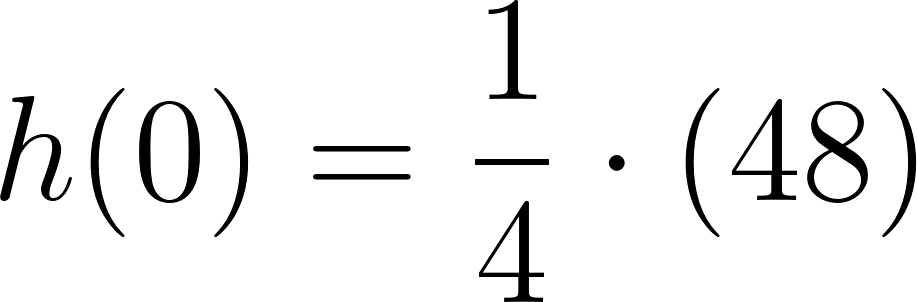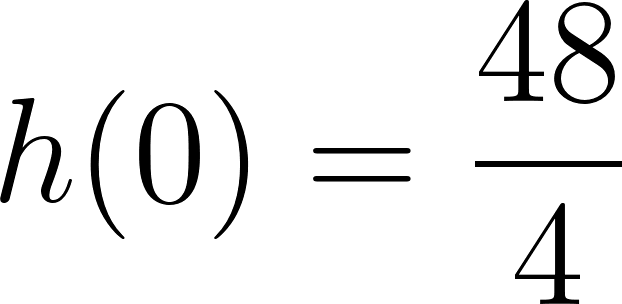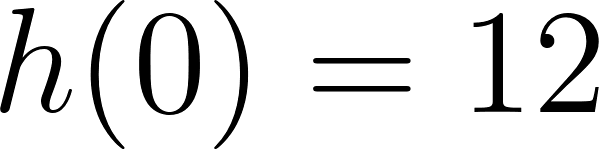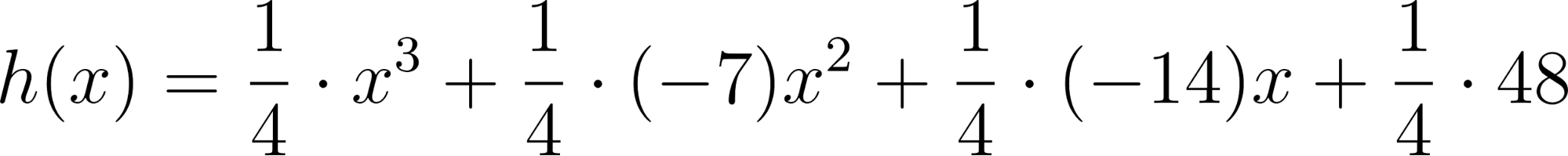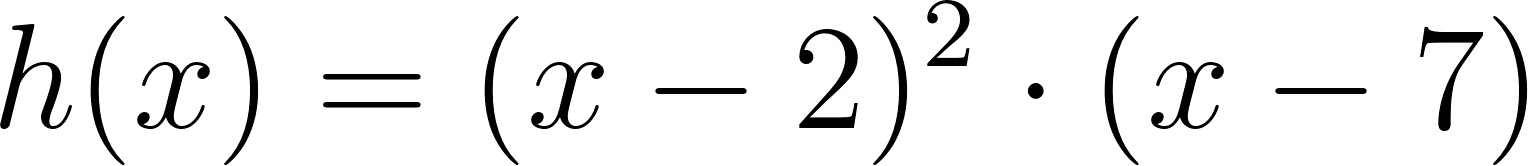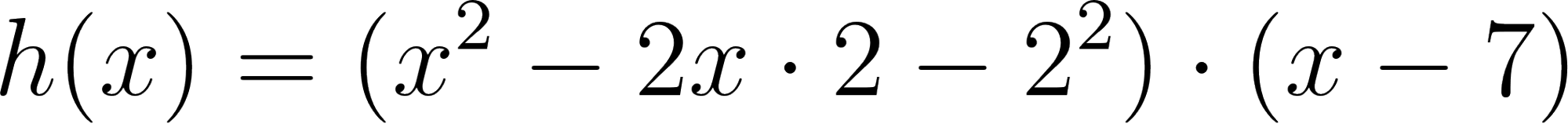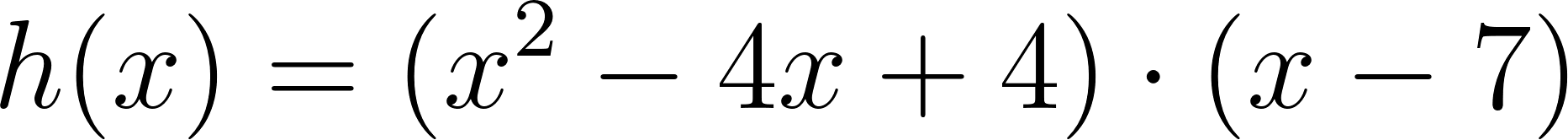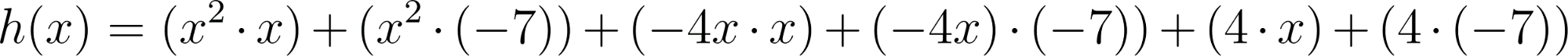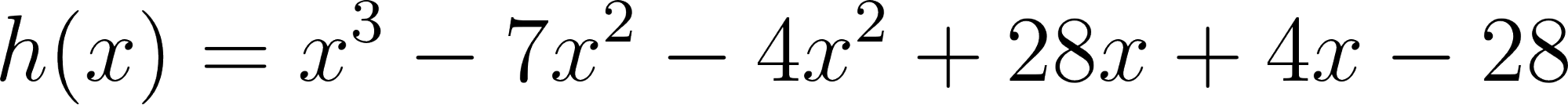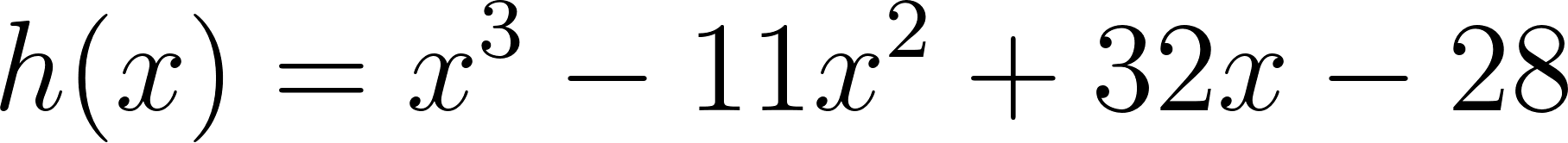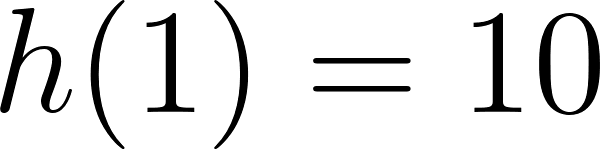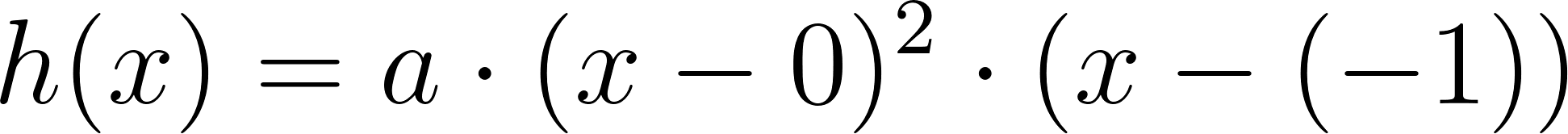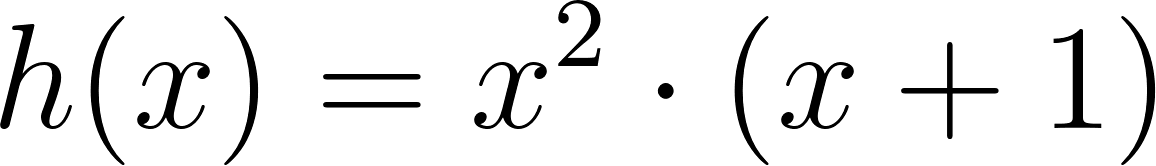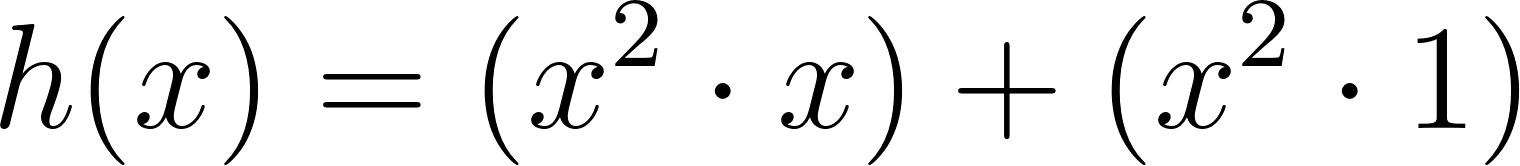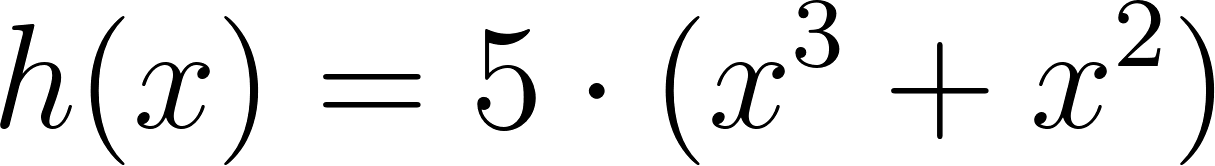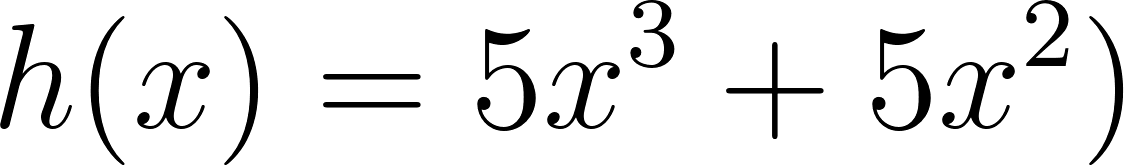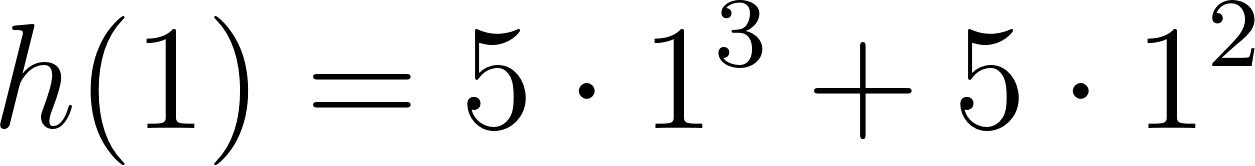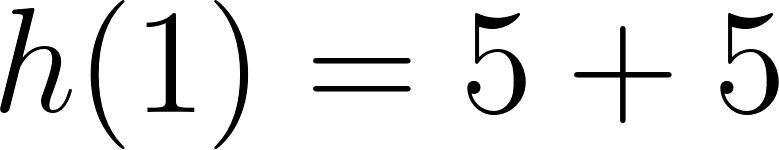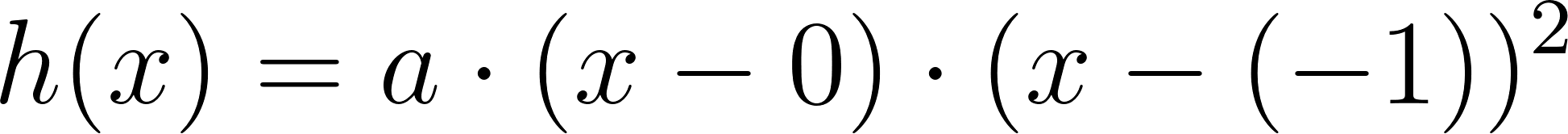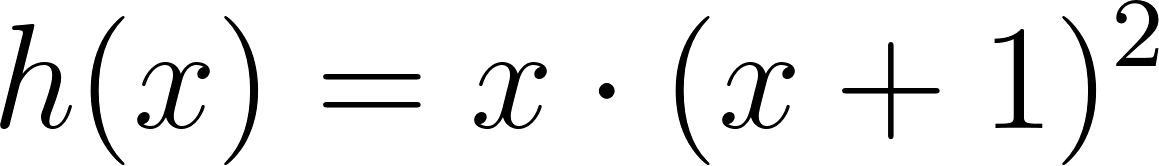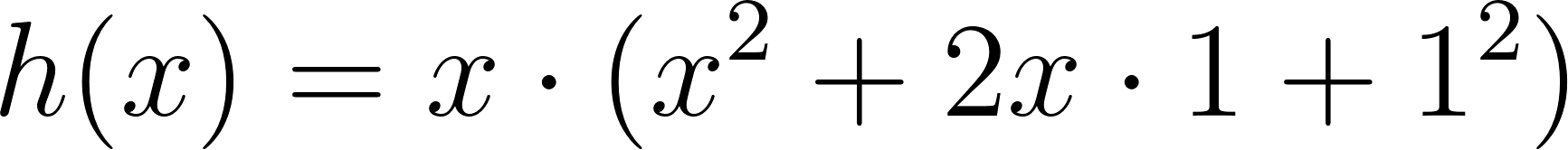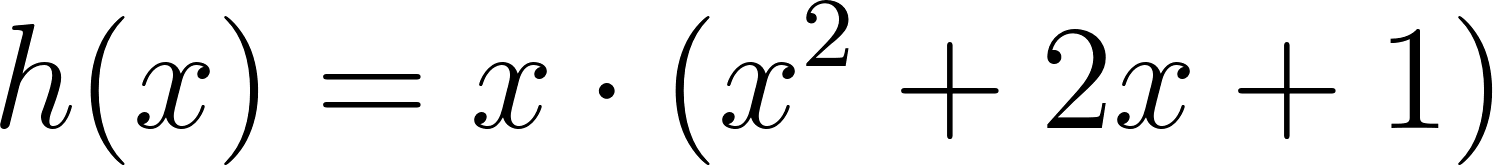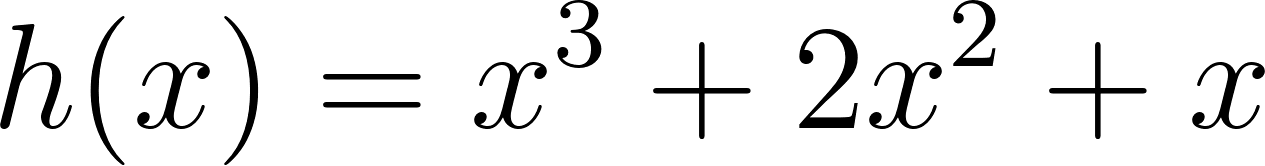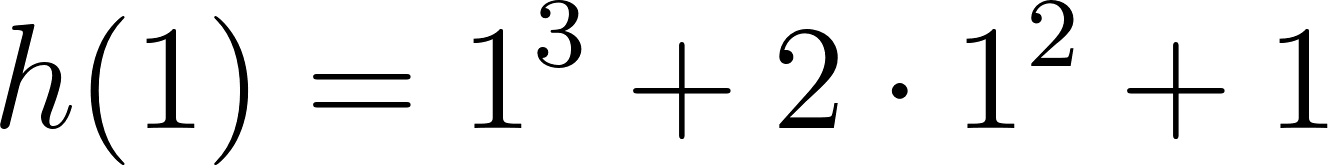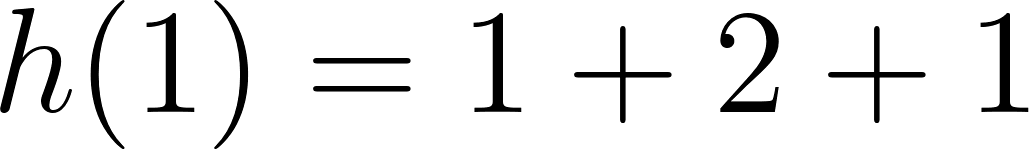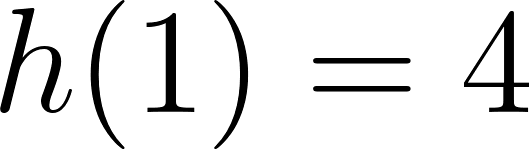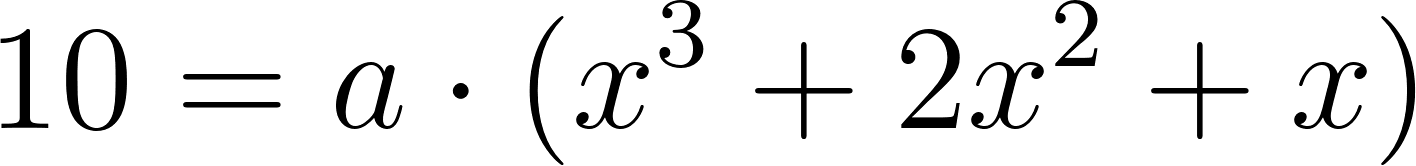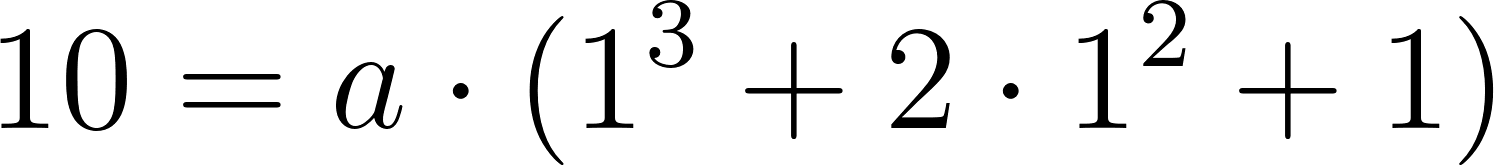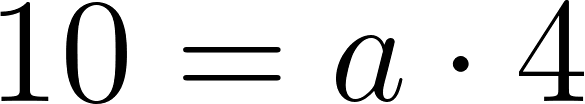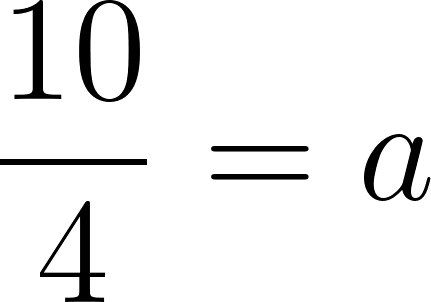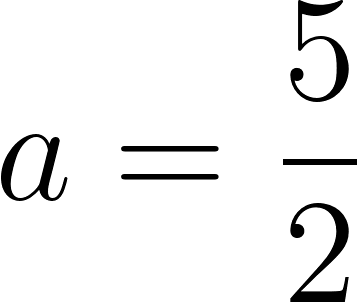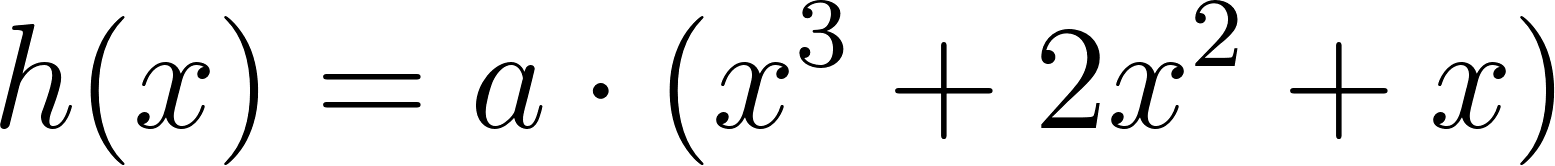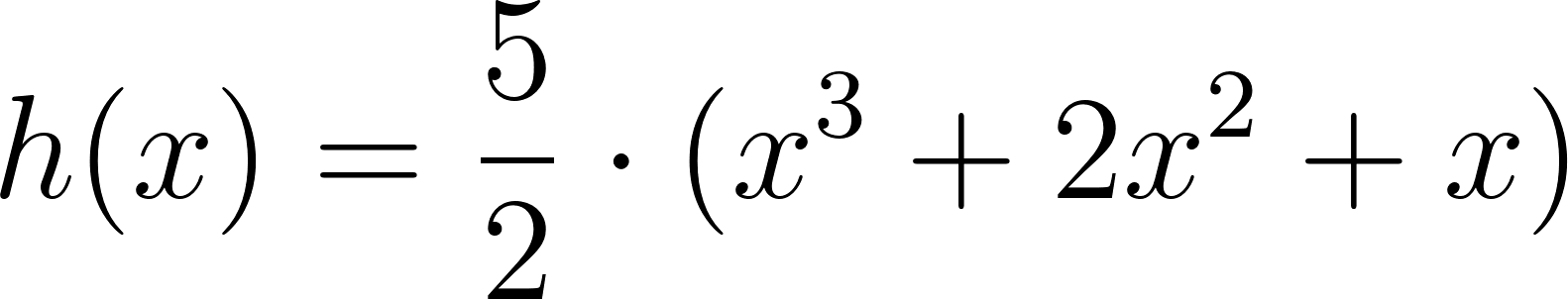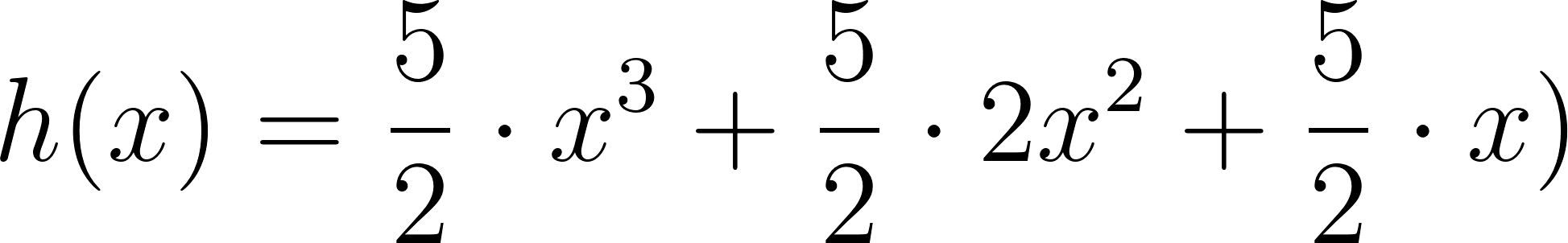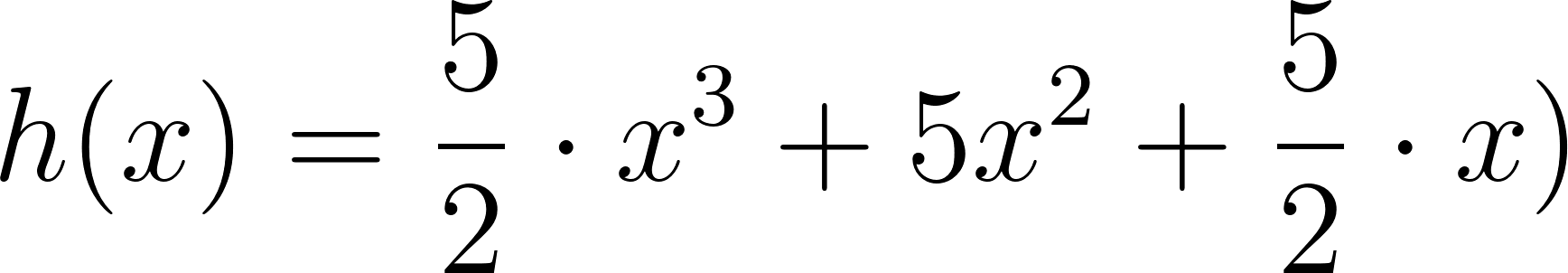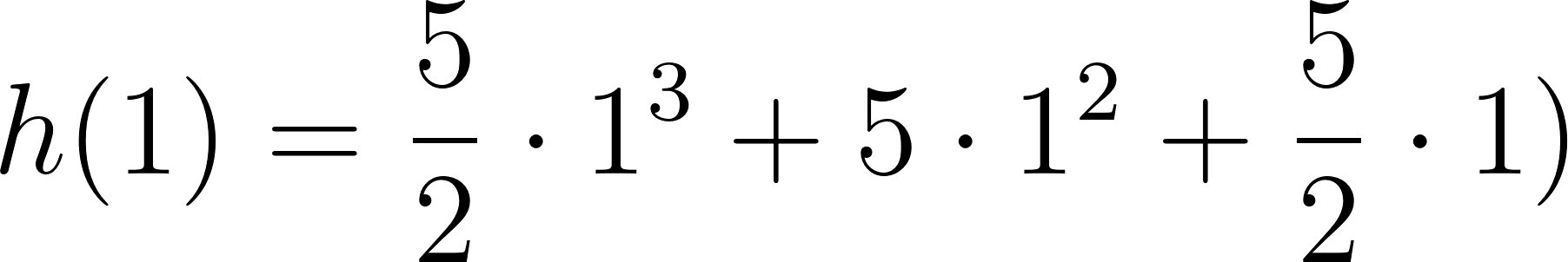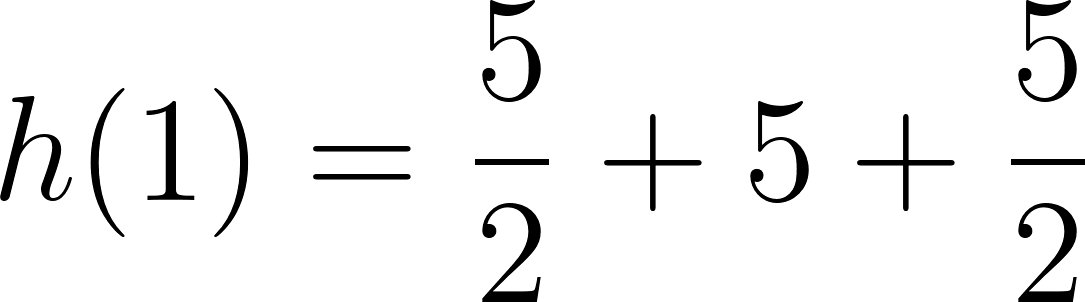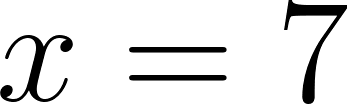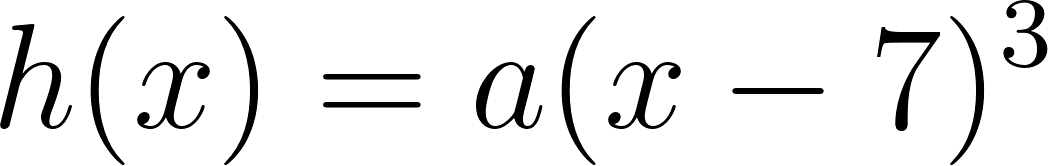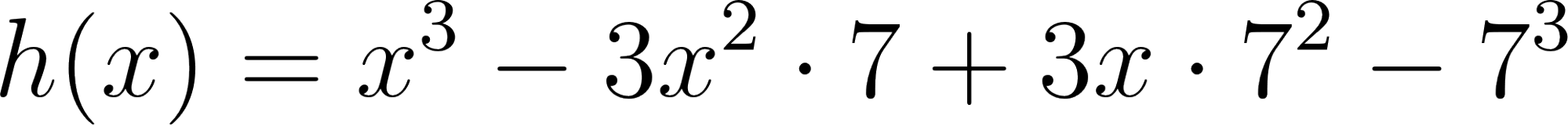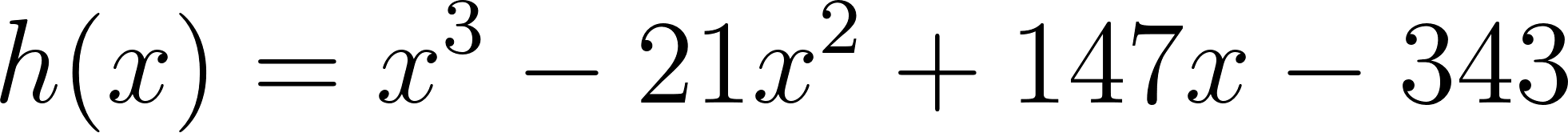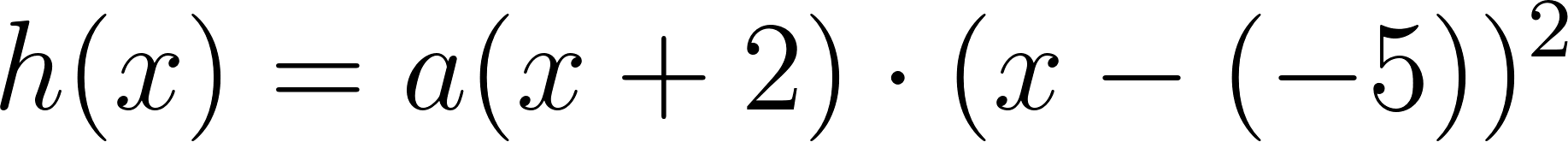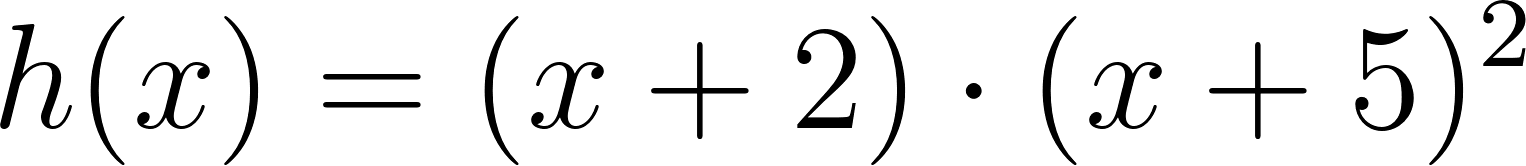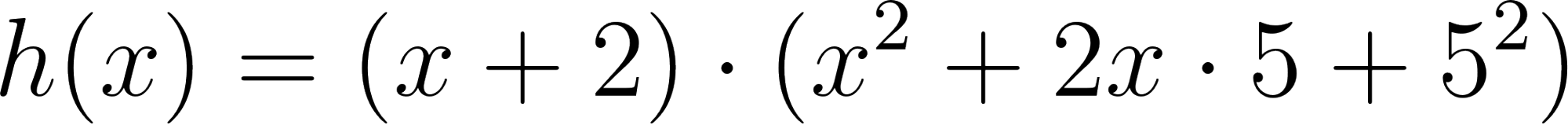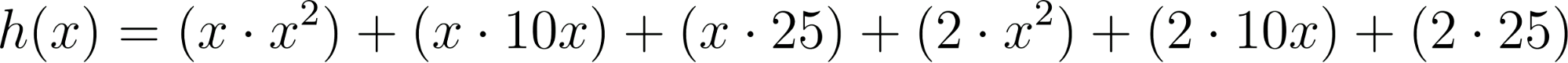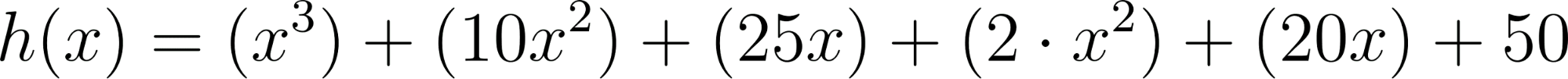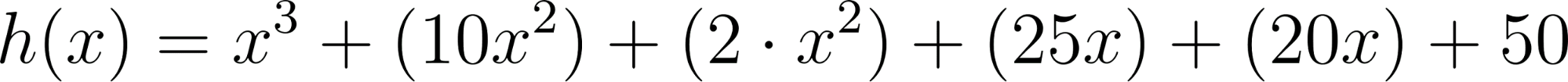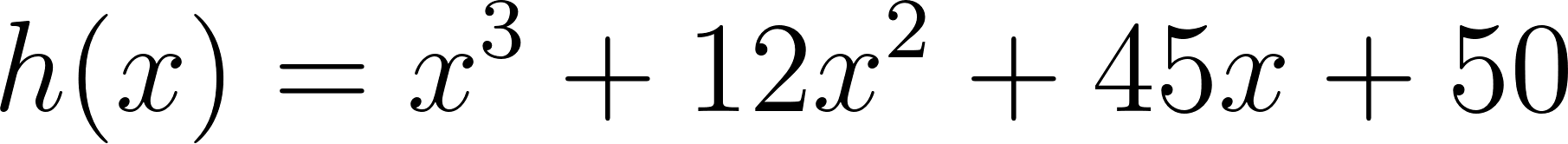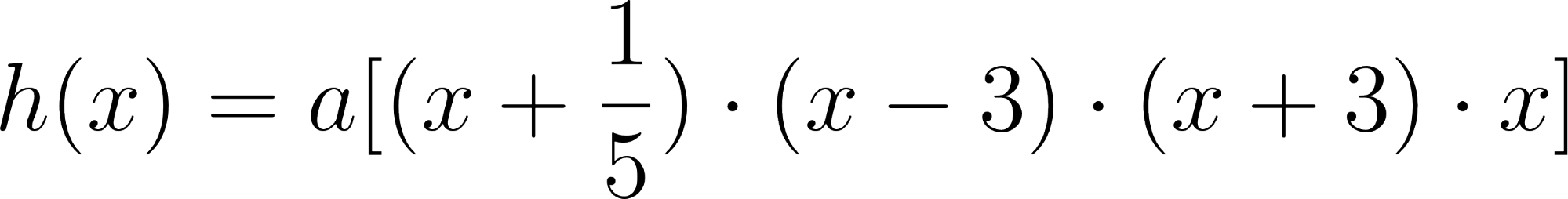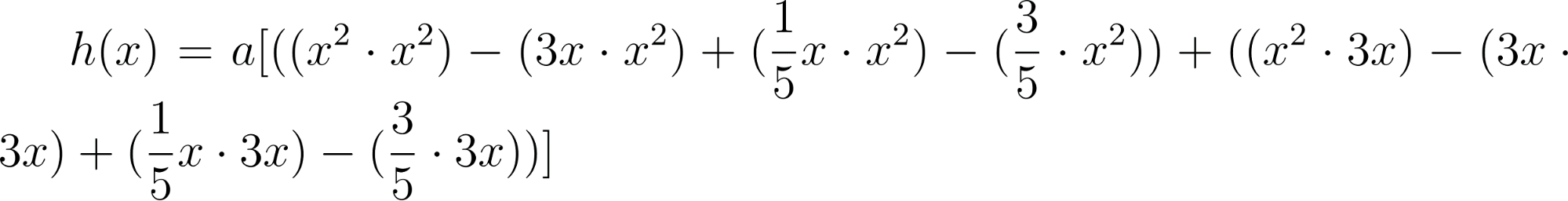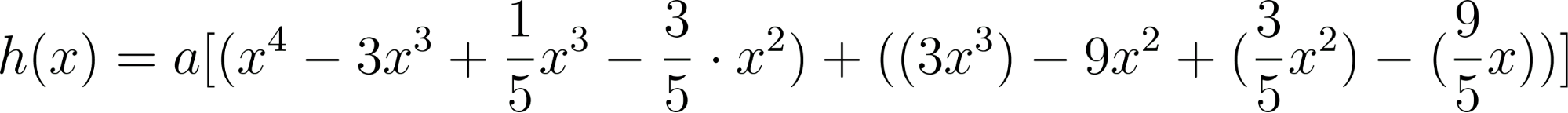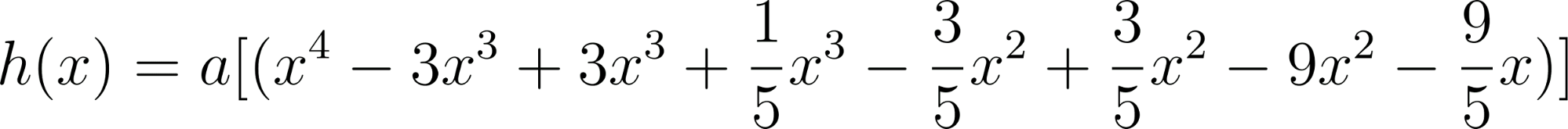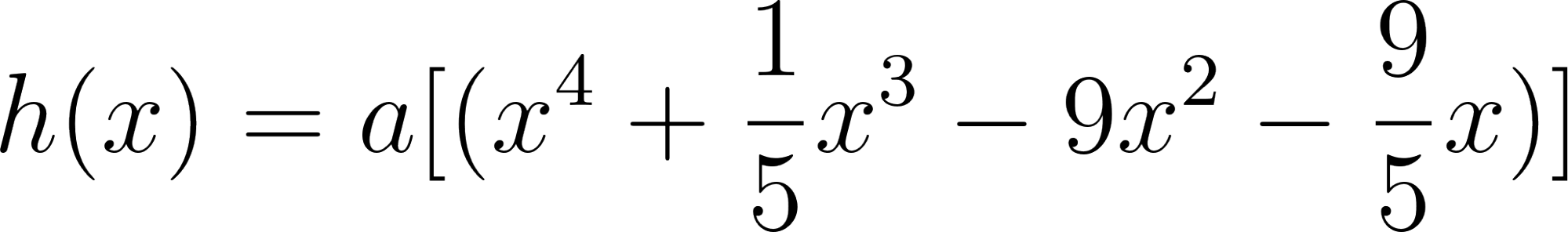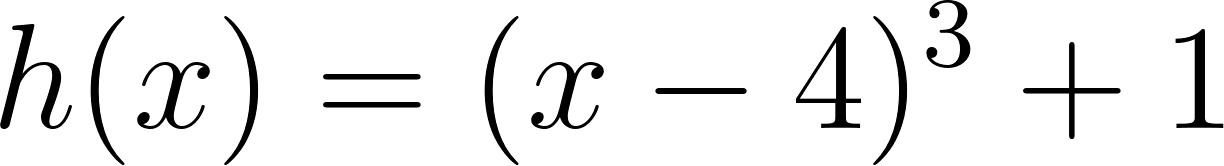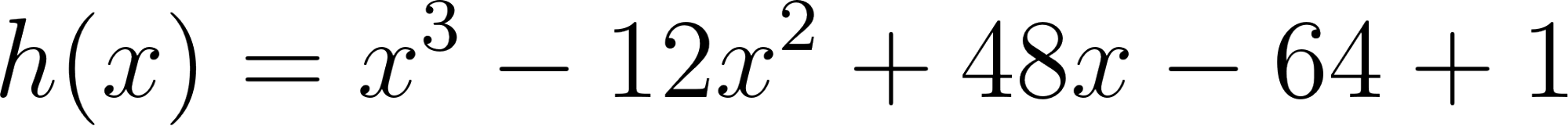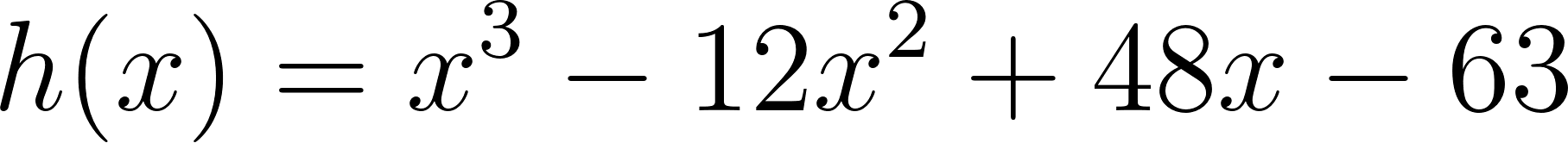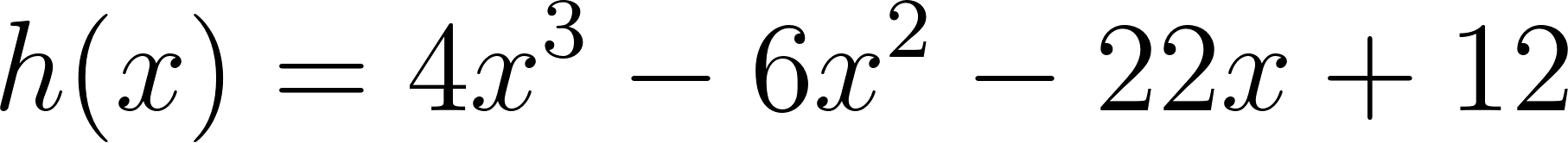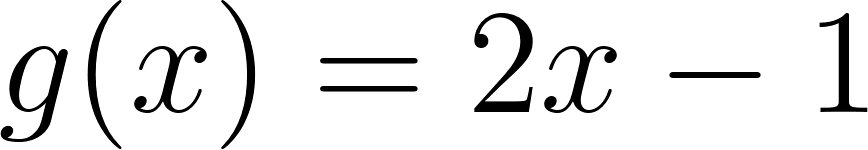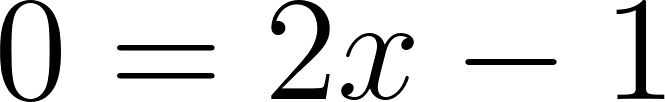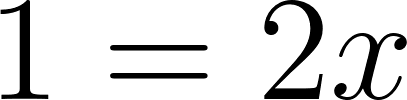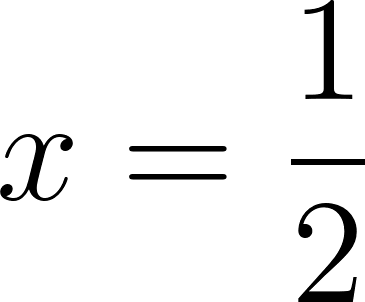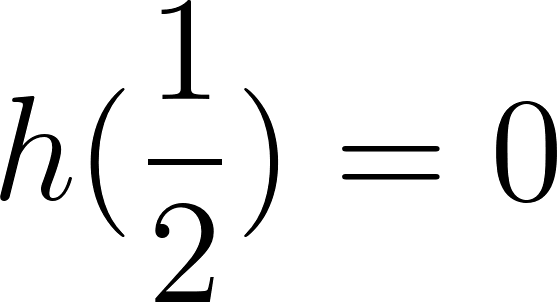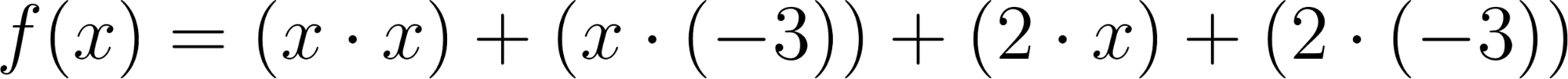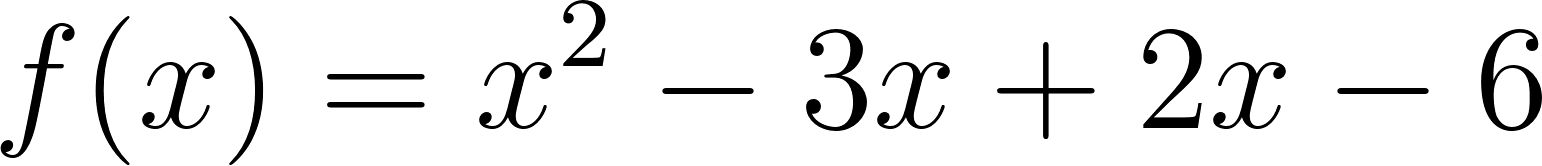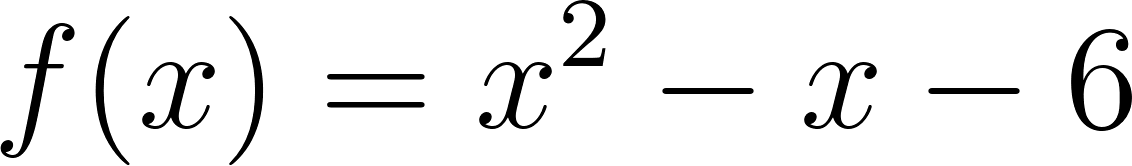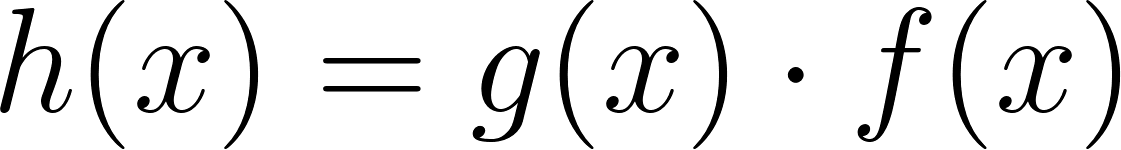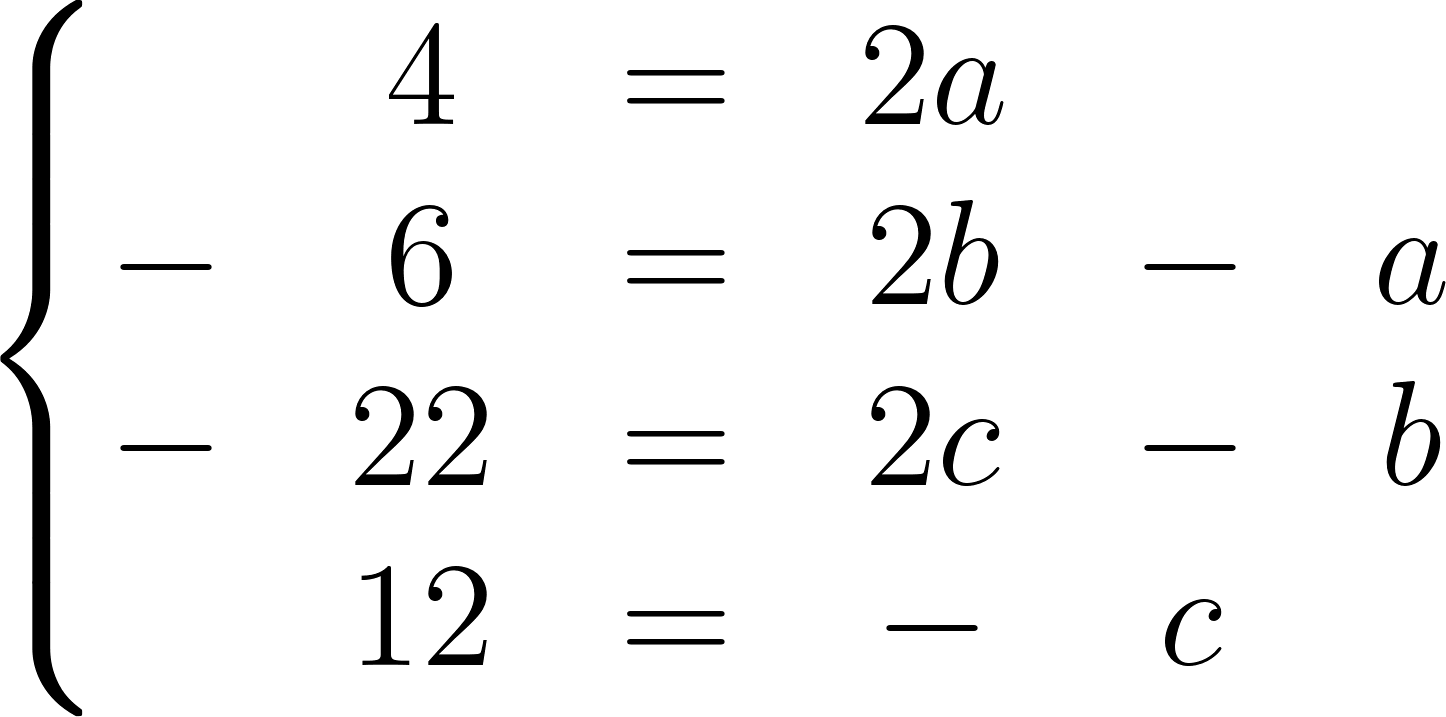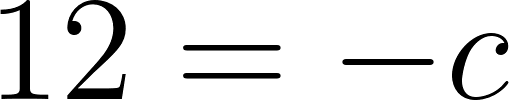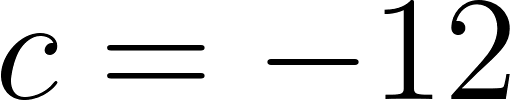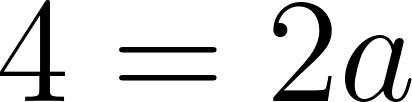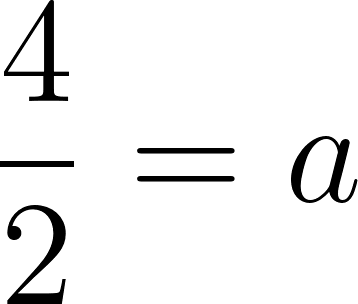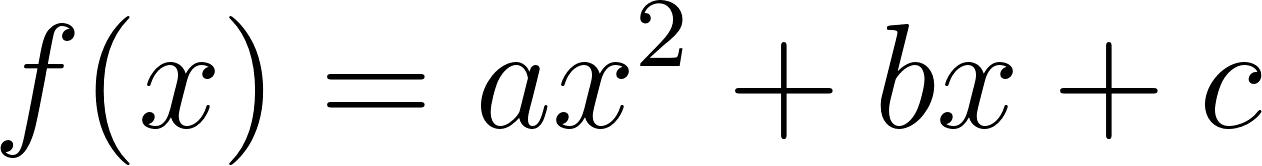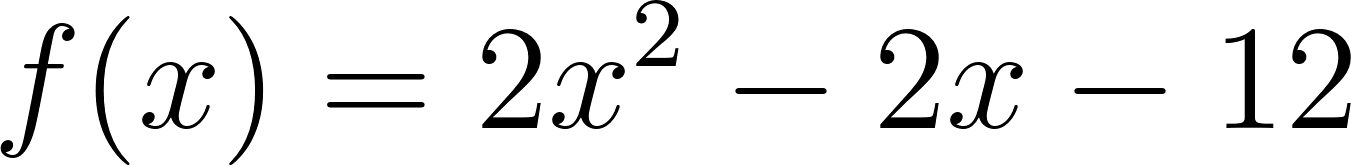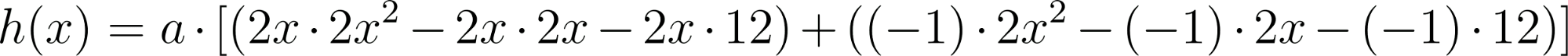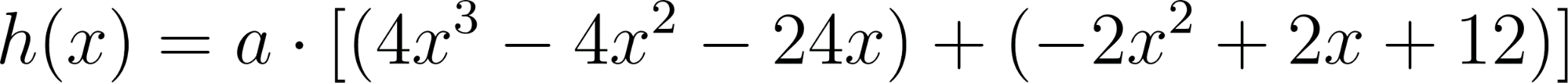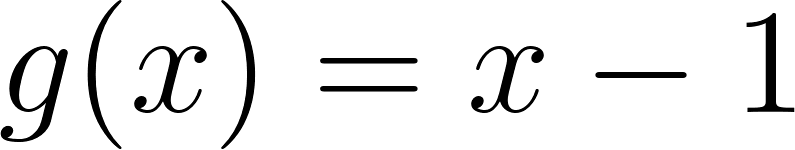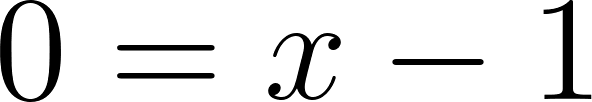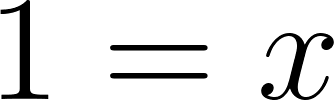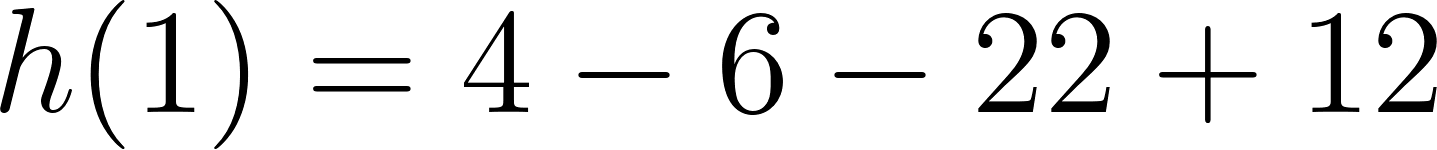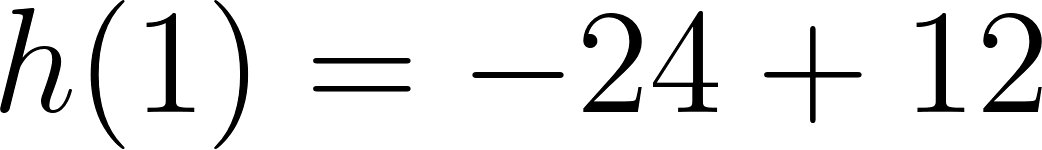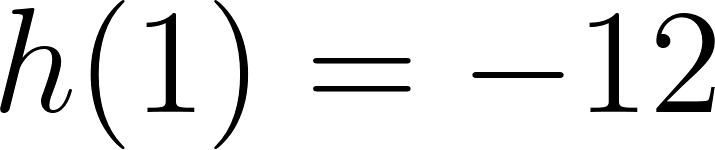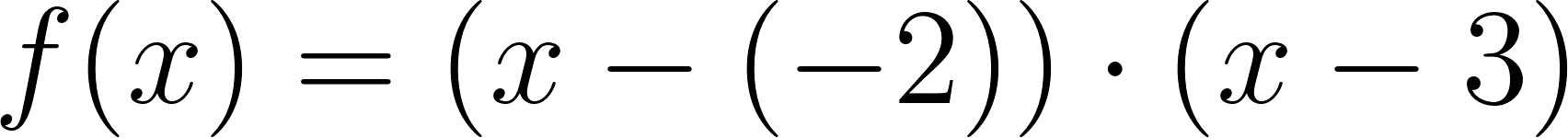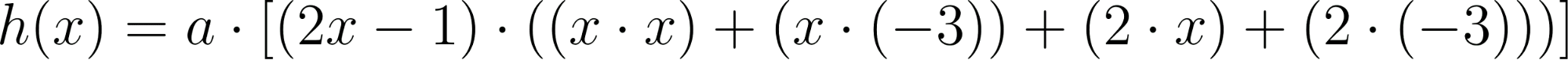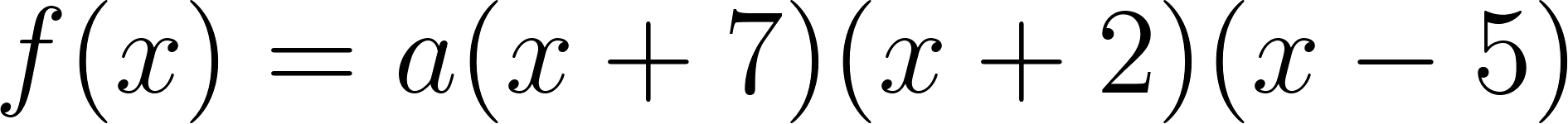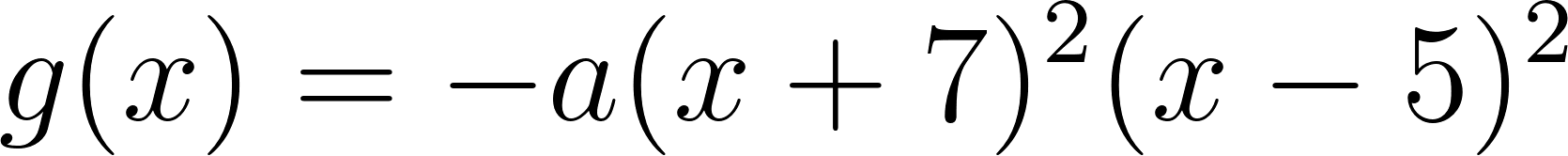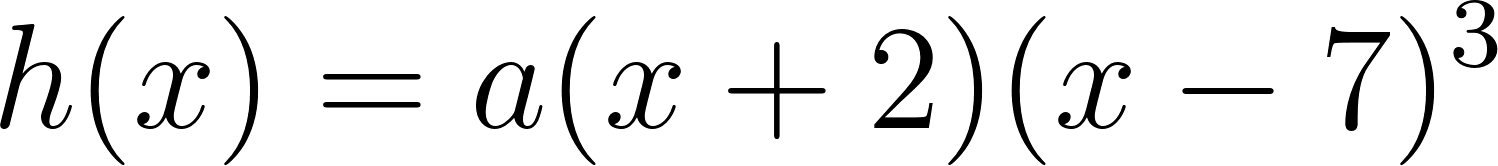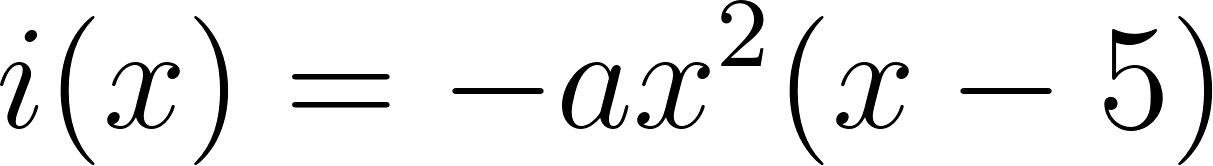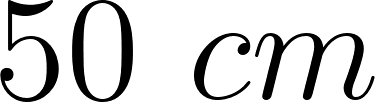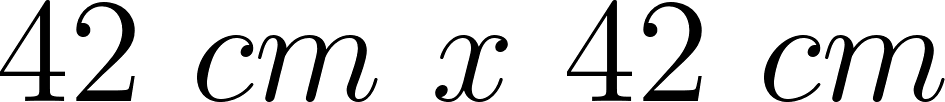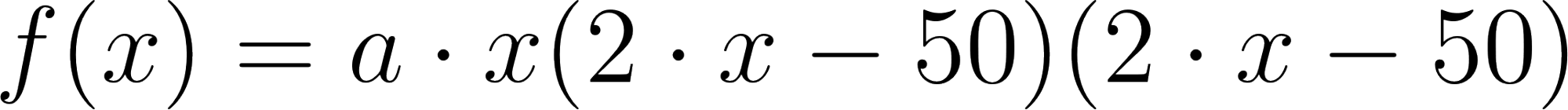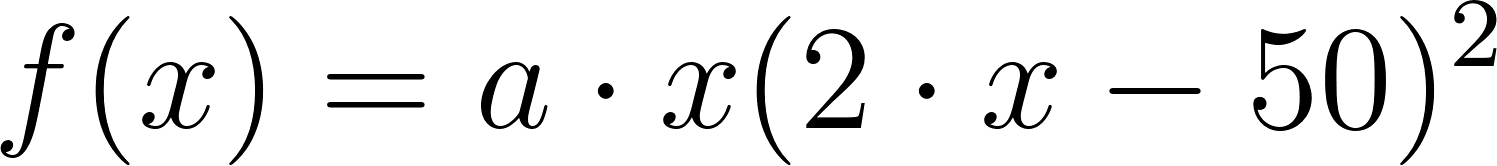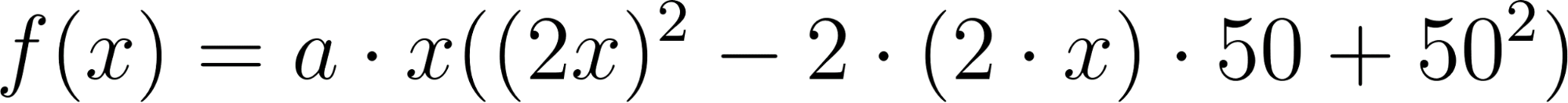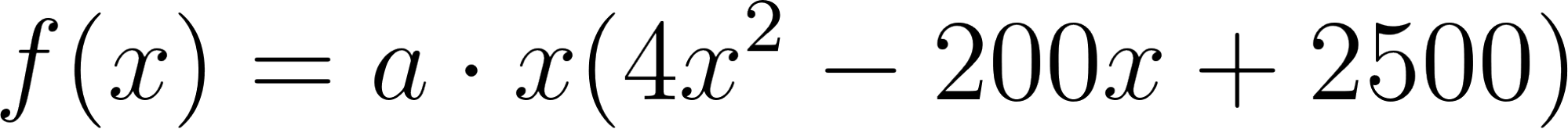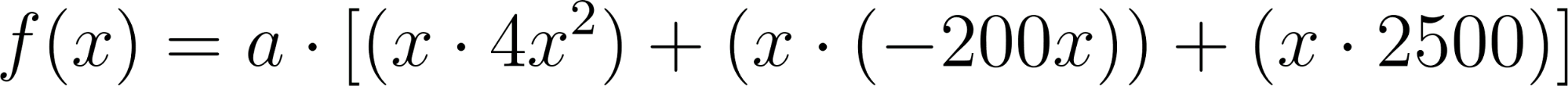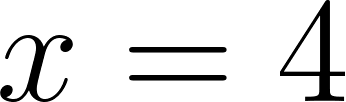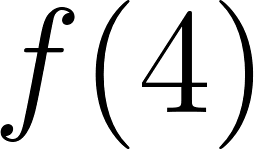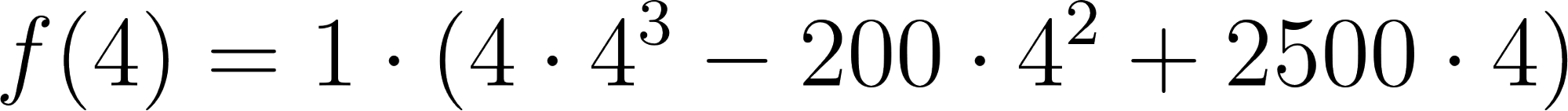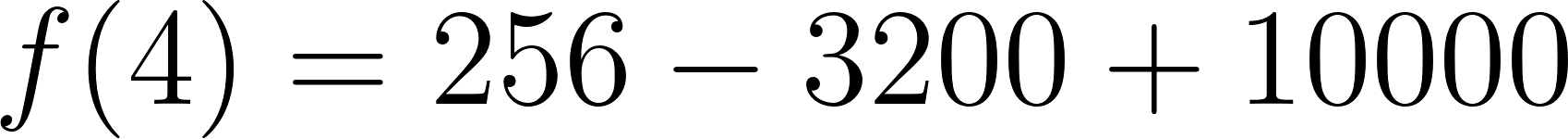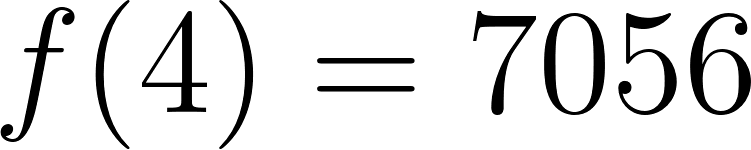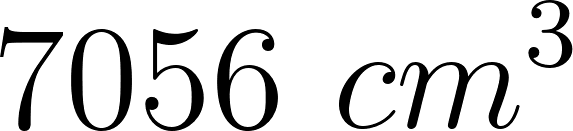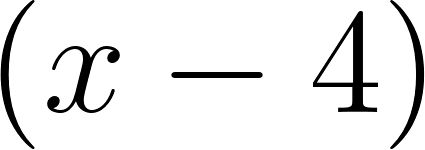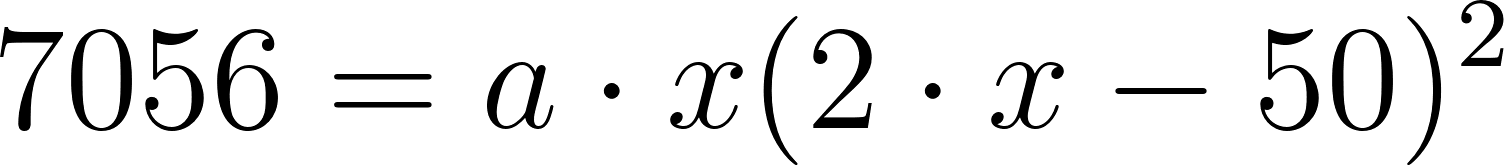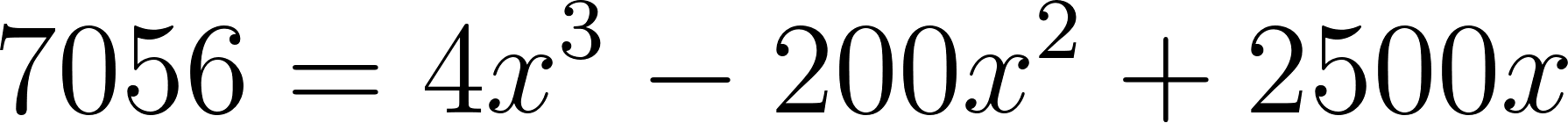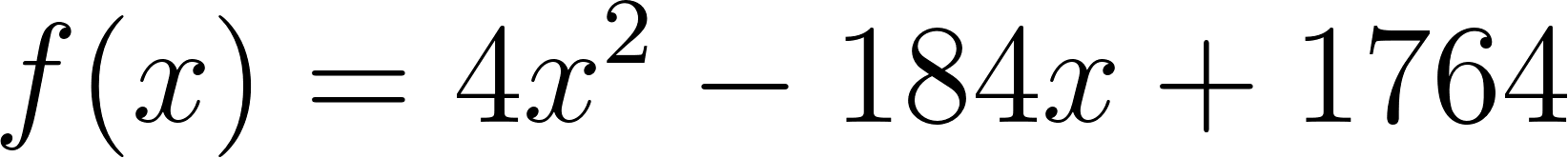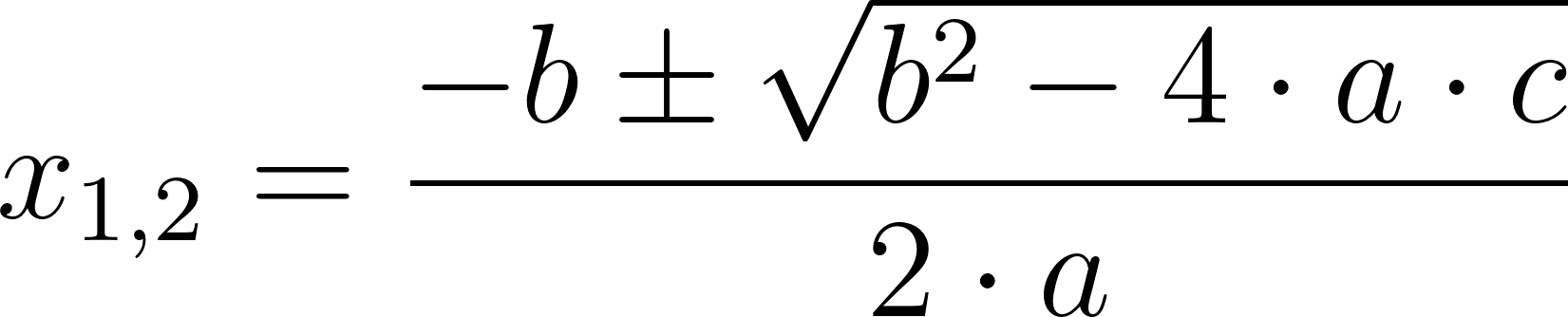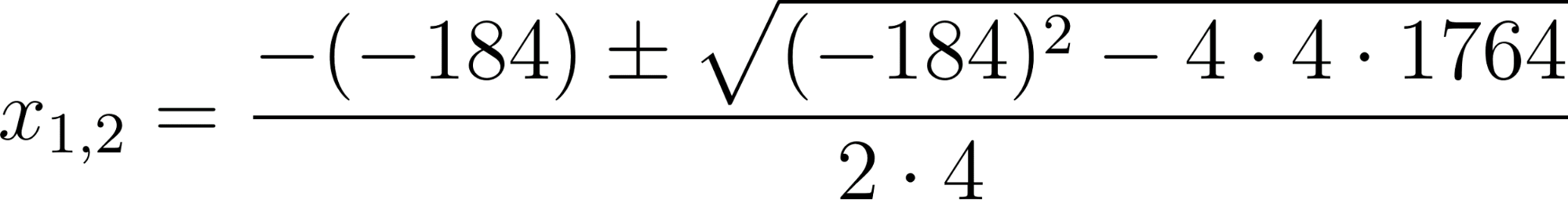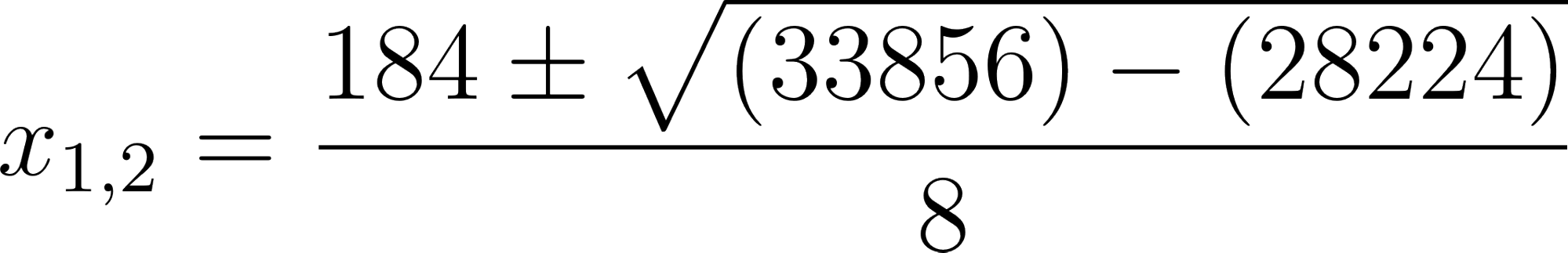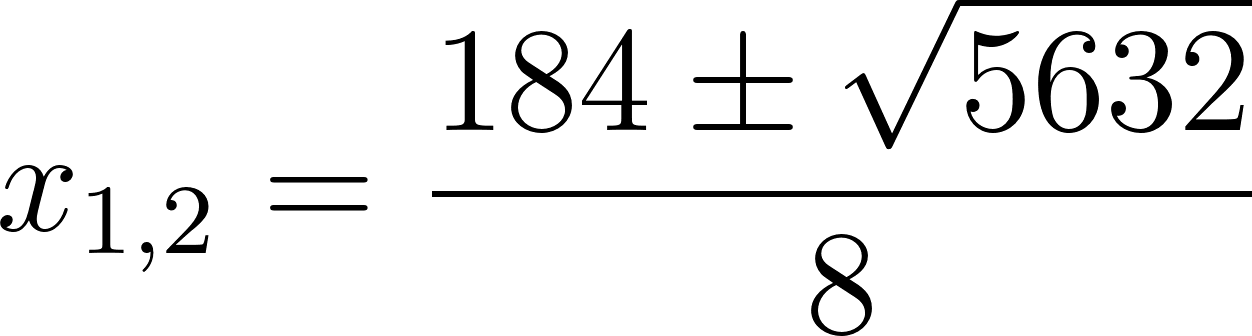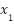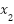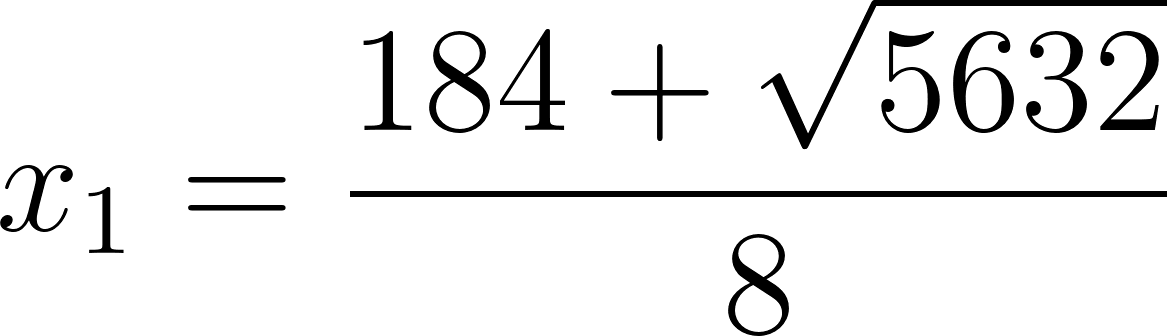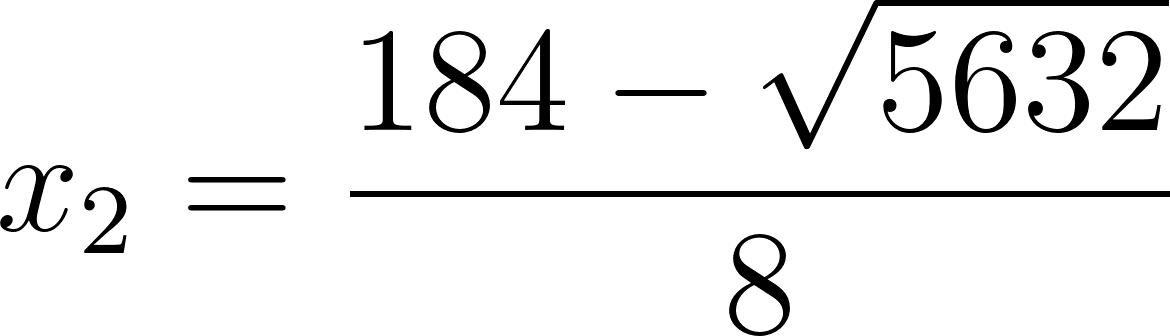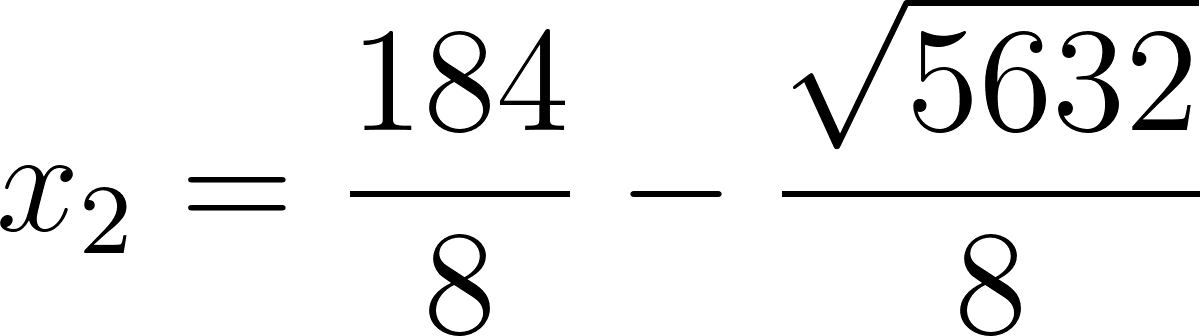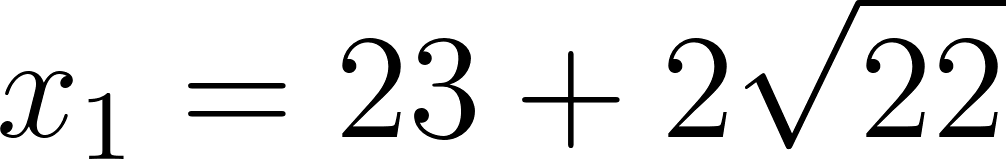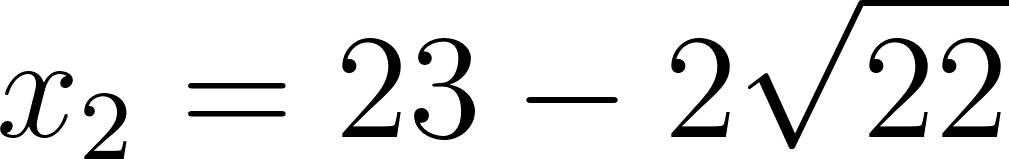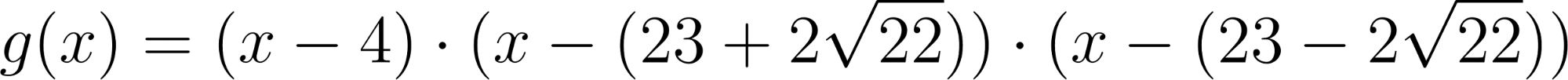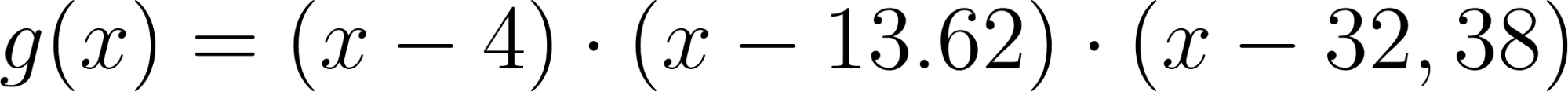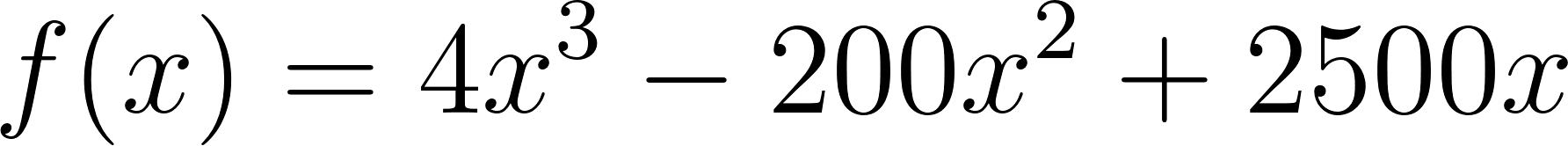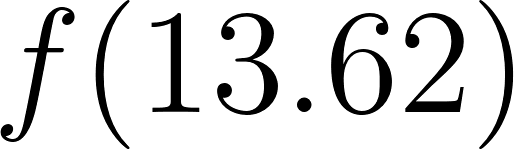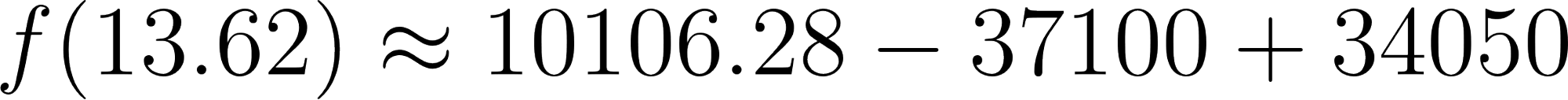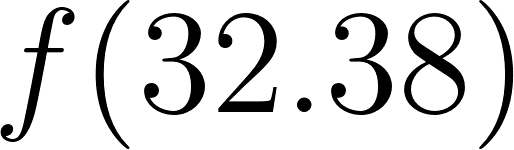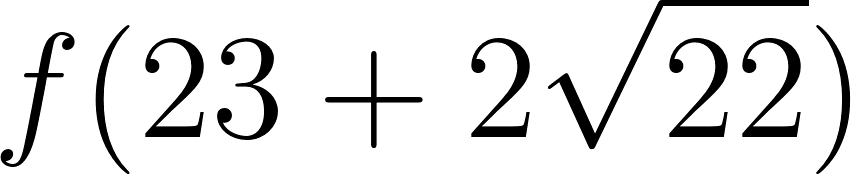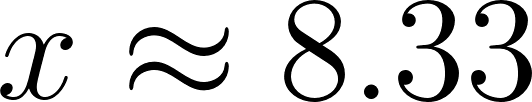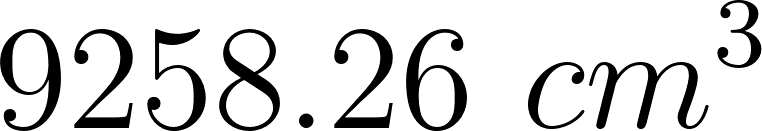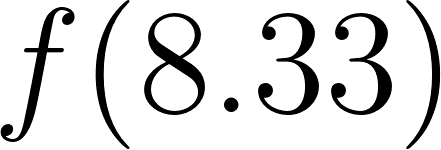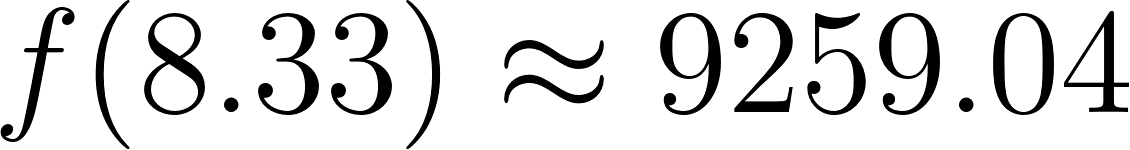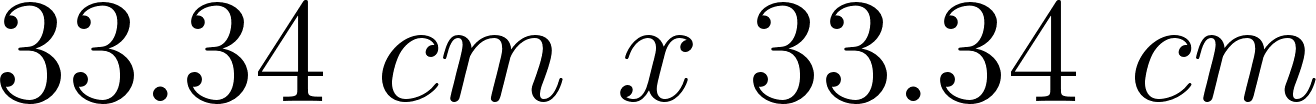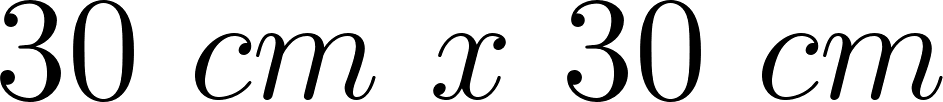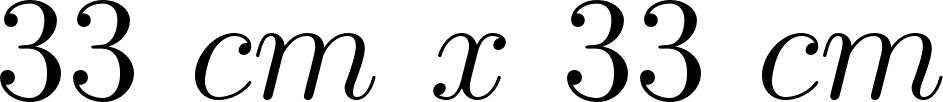Unidad 4
Función Polinómica
Las que casi todo lo pueden
Objetivos de esta unidad
|
- PROBLEMA
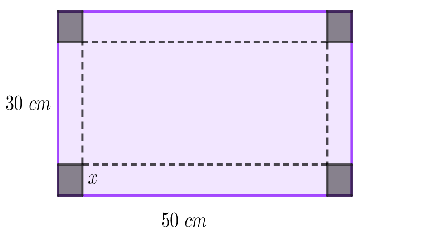
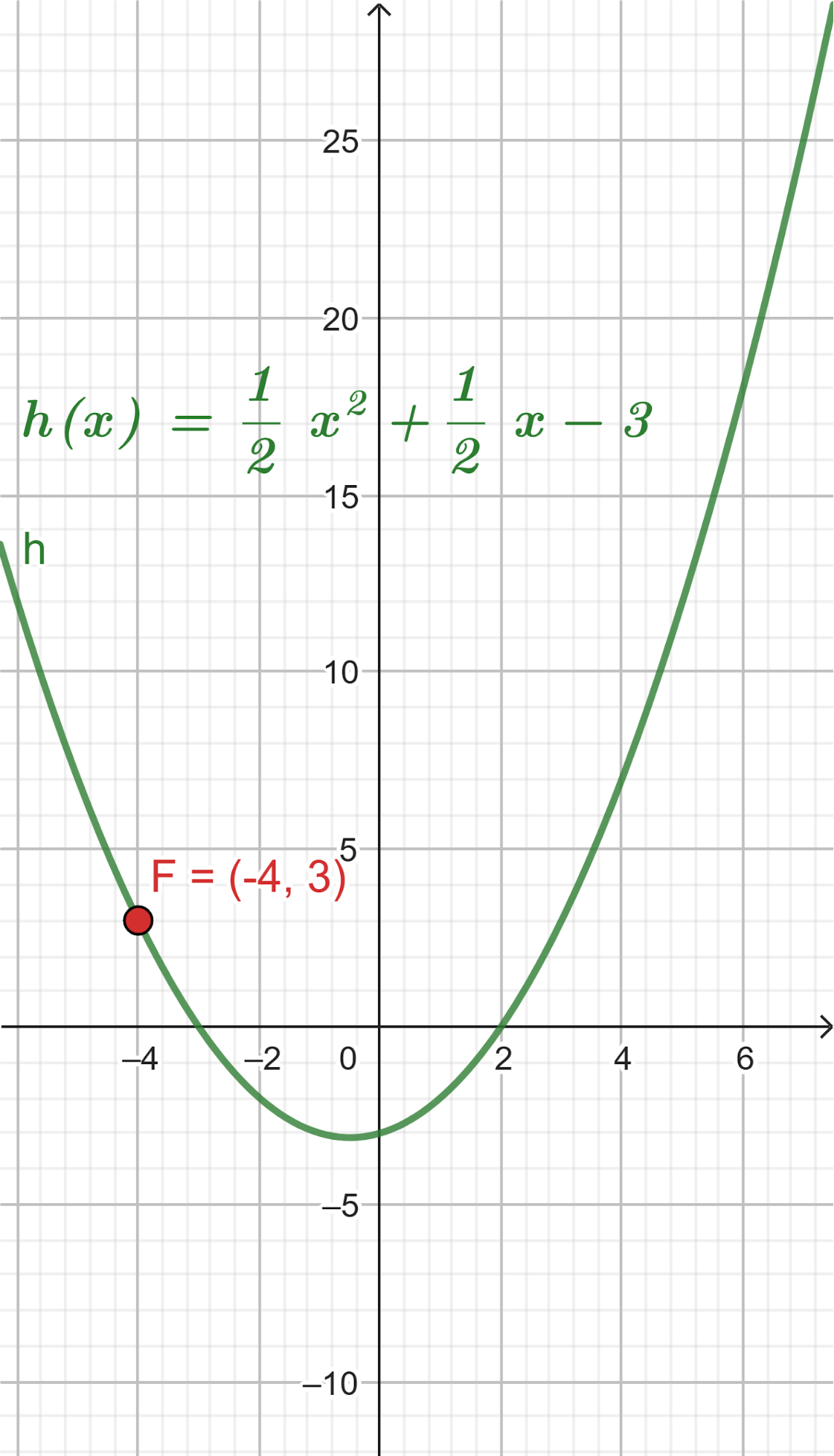
Cortando cuadrados iguales de las esquinas de una plancha de cartón de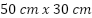 
, el cartón puede plegarse para formar una caja.
- Construyan (mentalmente, haciendo un dibujo o usando hojas rectangulares y una tijera, según necesiten) tres cajas de dimensiones distintas. Para cada una, calculen la altura, el área de la base y el volumen.
Solución:
- Altura=x con
- Área=b.h →
- Volúmen=b.h.x
- ¿Cómo puede ser la fórmula que permite calcular la altura de la caja en función de lo que mida el lado de los cuadrados cortados en las esquinas de la plancha de cartón?
Solución:
- ¿Cómo puede ser la fórmula que permite calcular el área de la base de la caja en función de lo que mida el lado de los cuadrados cortados en las esquinas de la plancha de cartón?
Solución:
- ¿Cómo puede ser la fórmula que permite calcular el volumen de la caja en función de lo que mida el lado de los cuadrados cortados en las esquinas de la plancha de cartón?
Solución:
- Indiquen el dominio de la función que da el volumen, teniendo en cuenta el contexto del problema.
Solución:
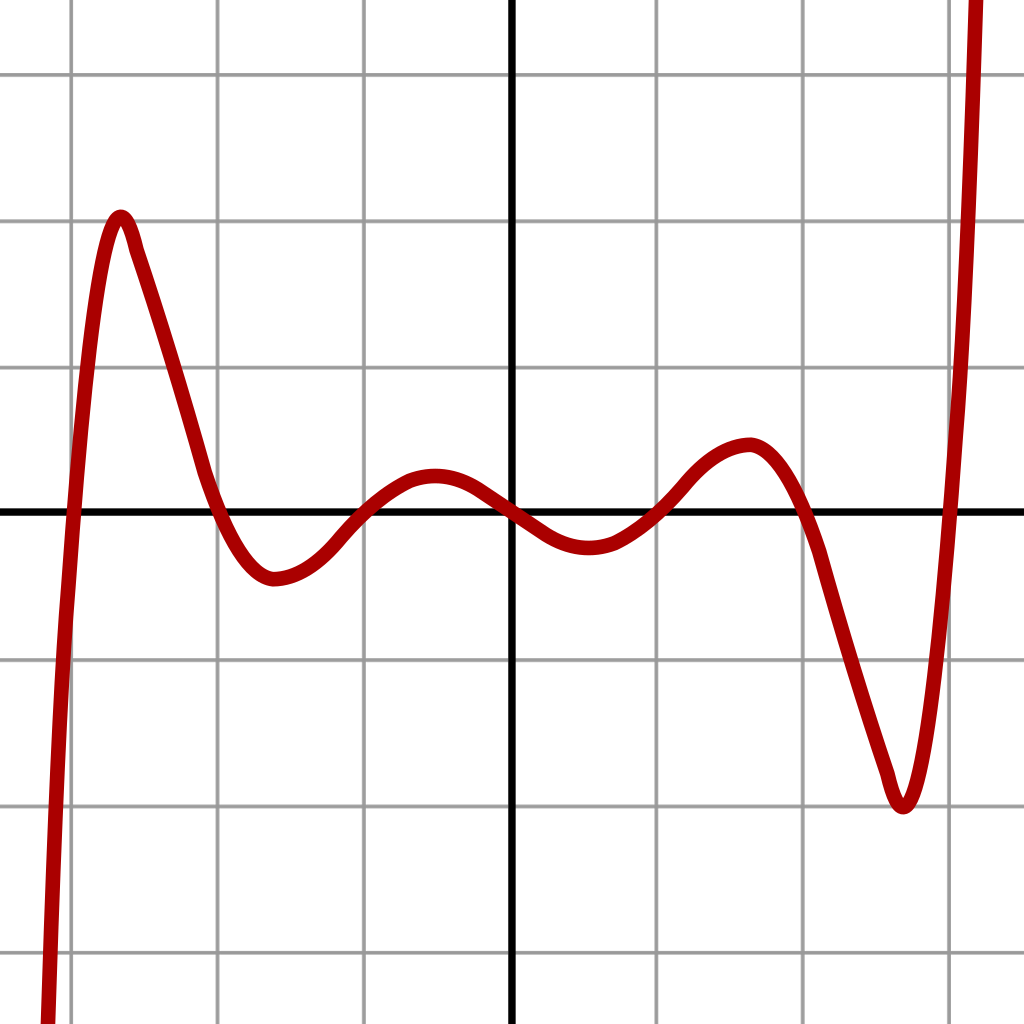
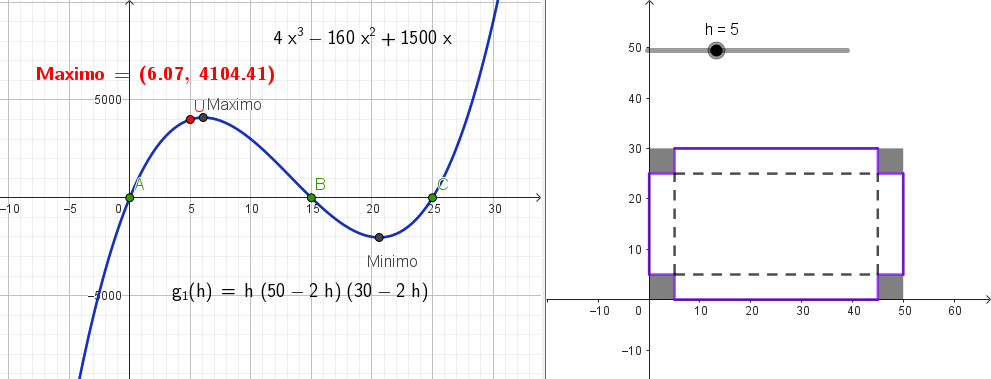
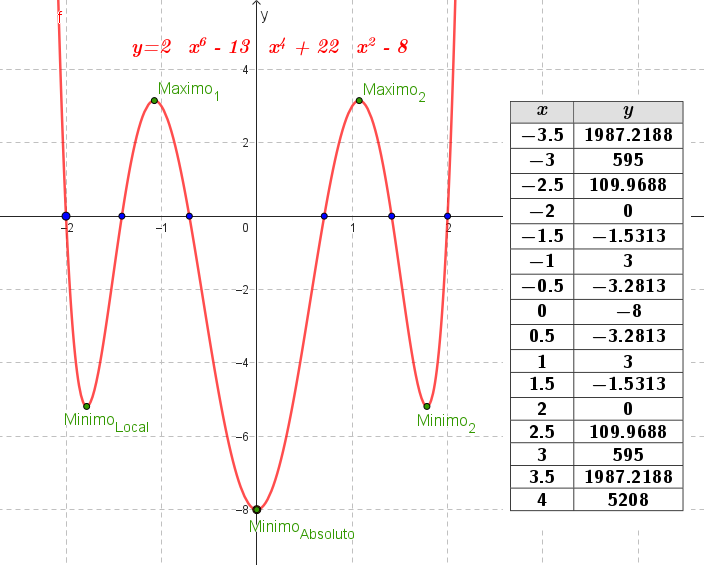
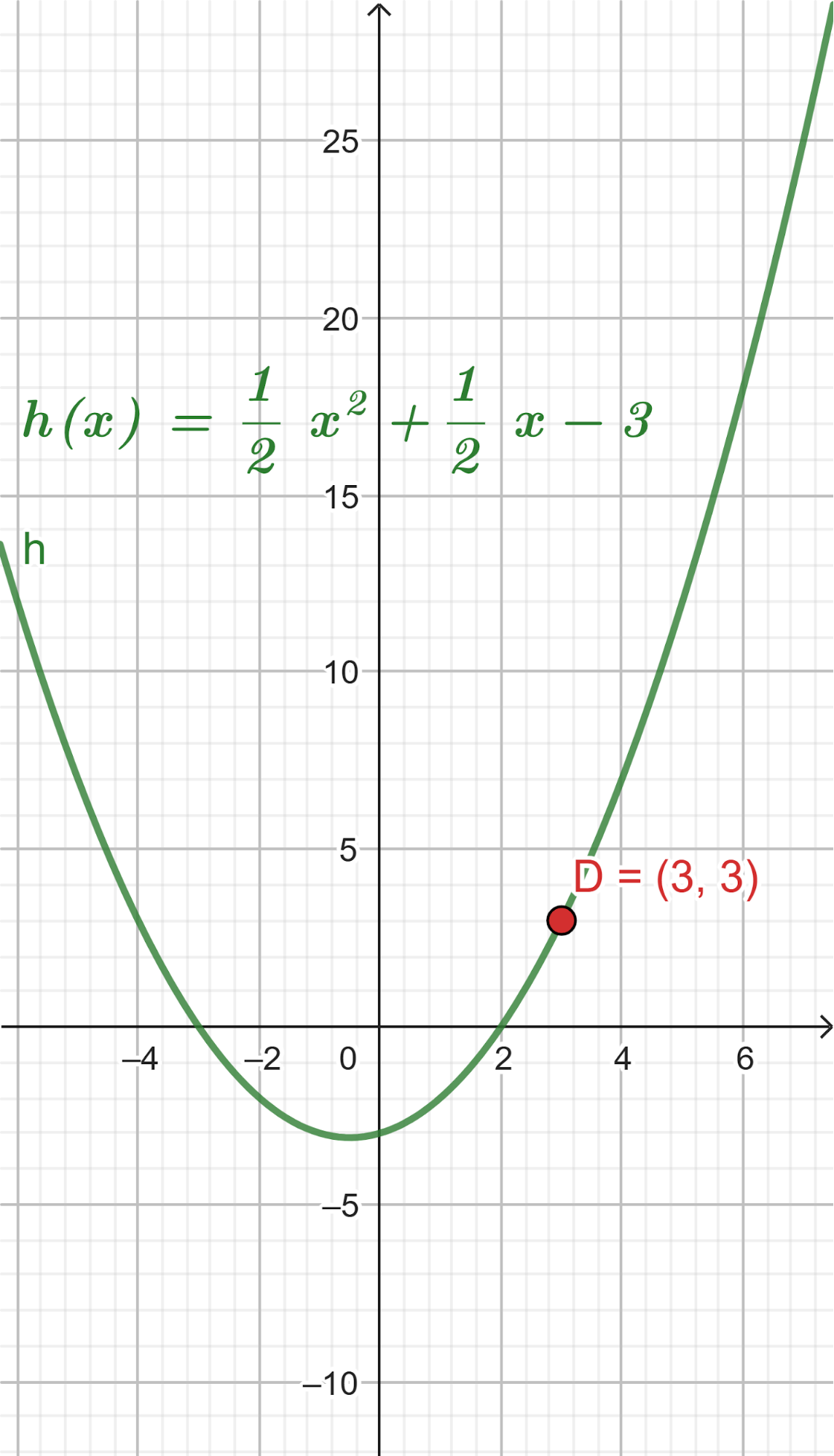
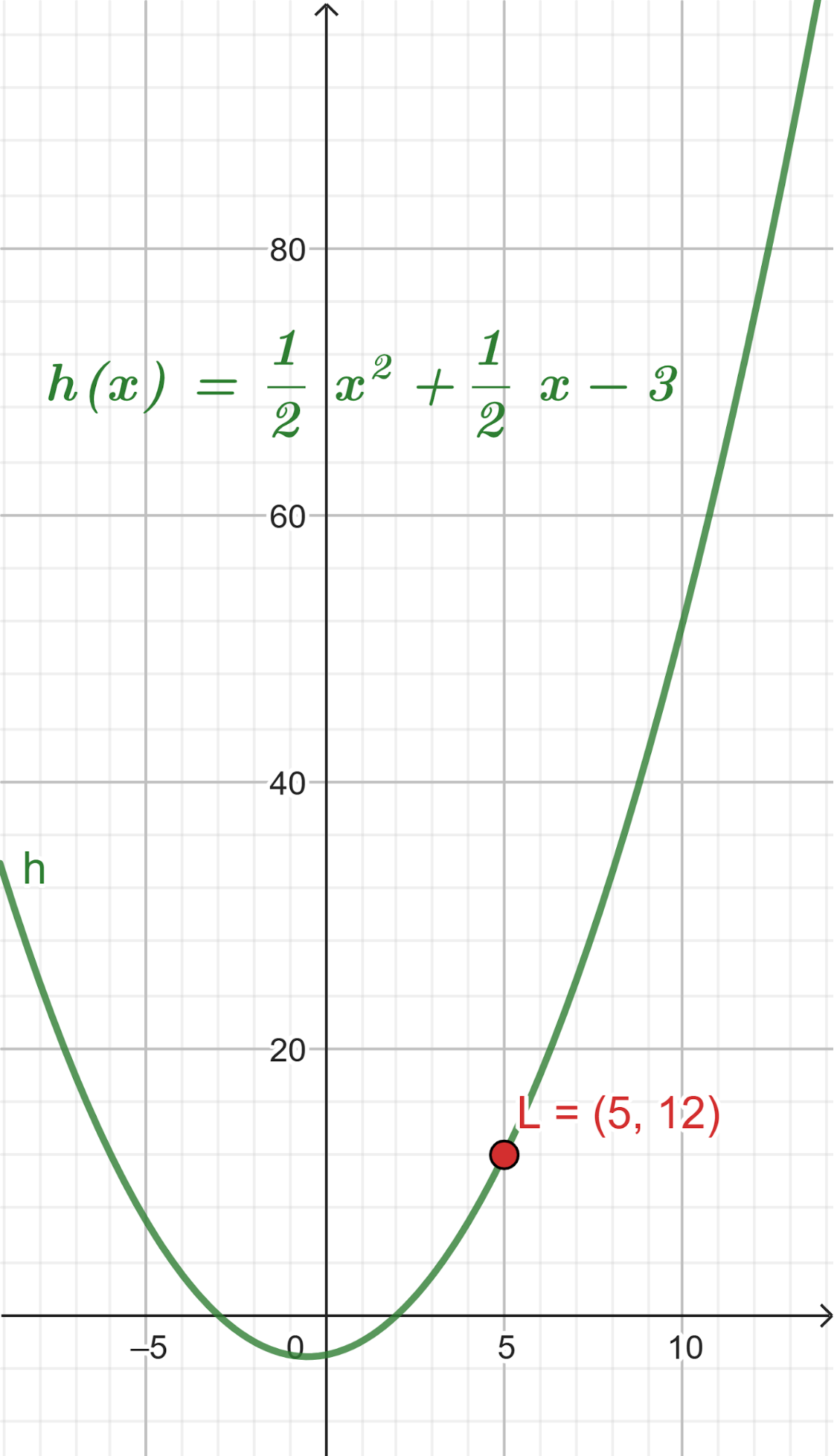
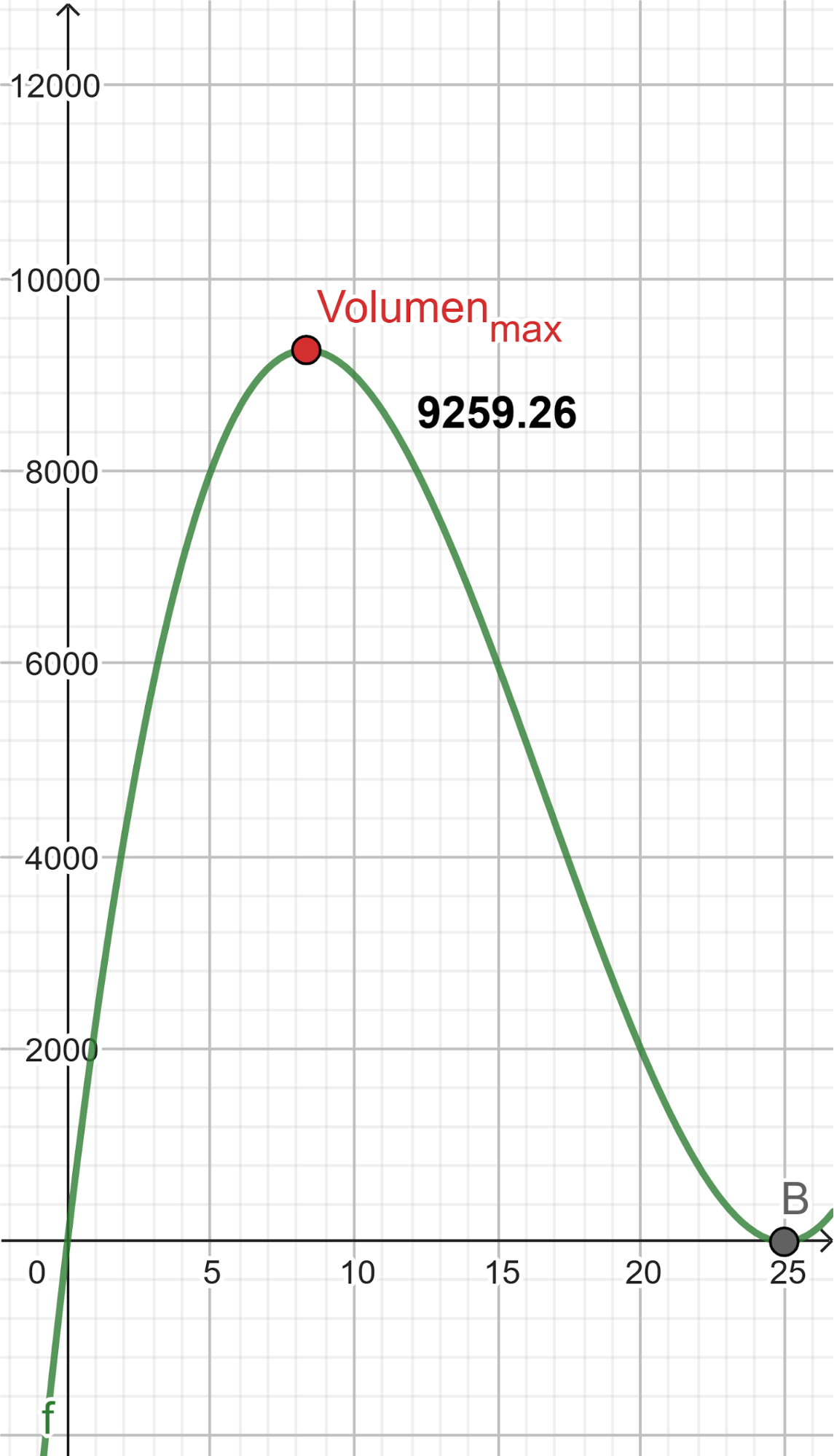
- Grafiquen la función que da el volumen y analicen para qué valor del lado del cuadrado cortado resulta el volumen máximo posible. Expliquen su respuesta.
Solución:
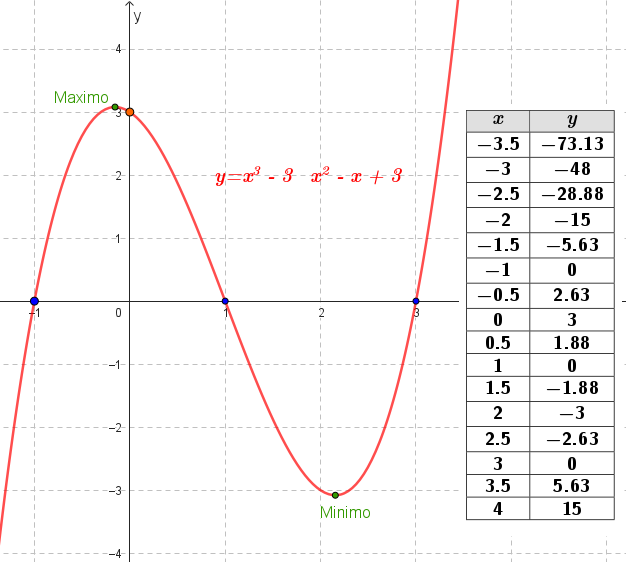
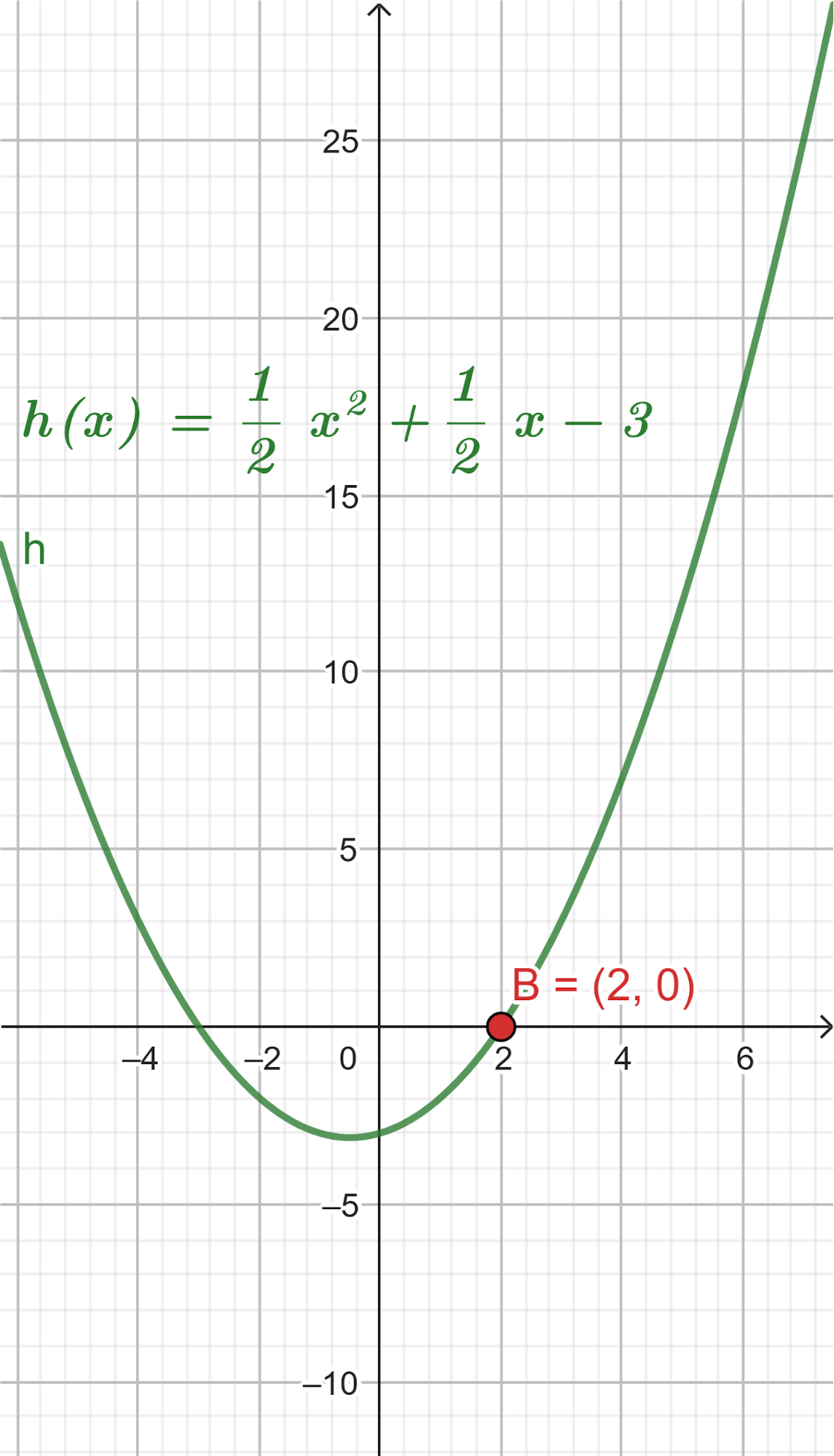
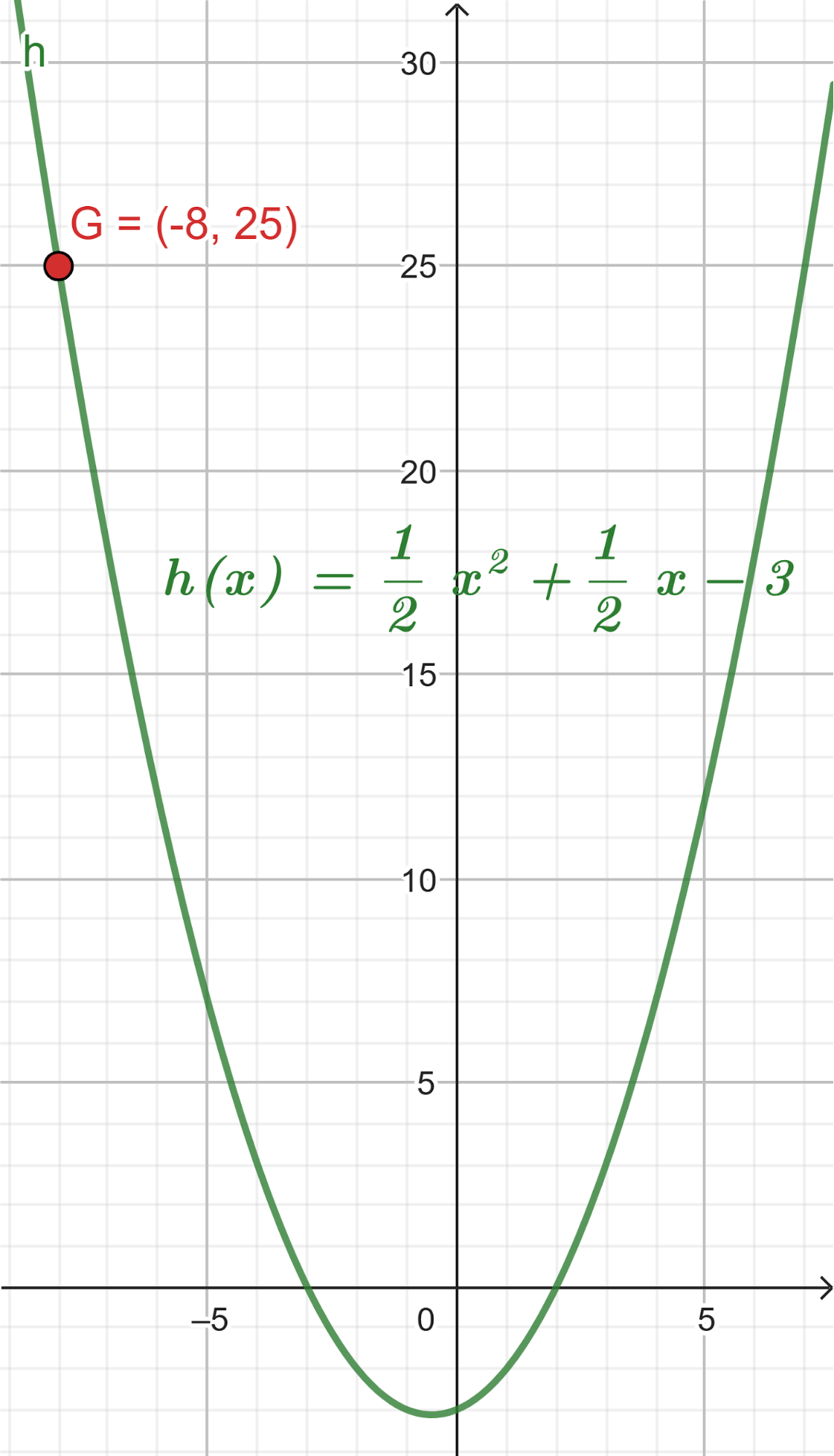
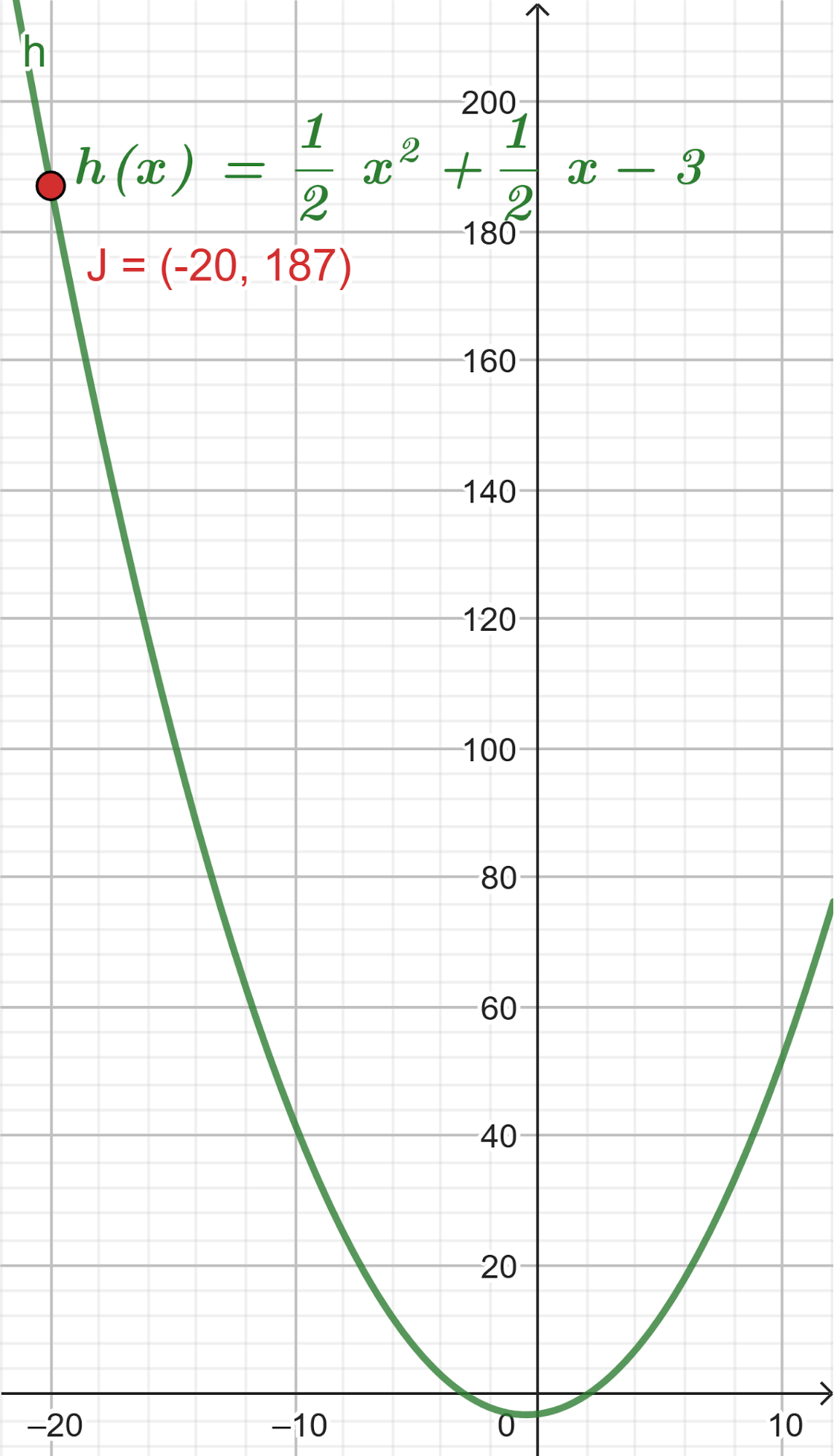
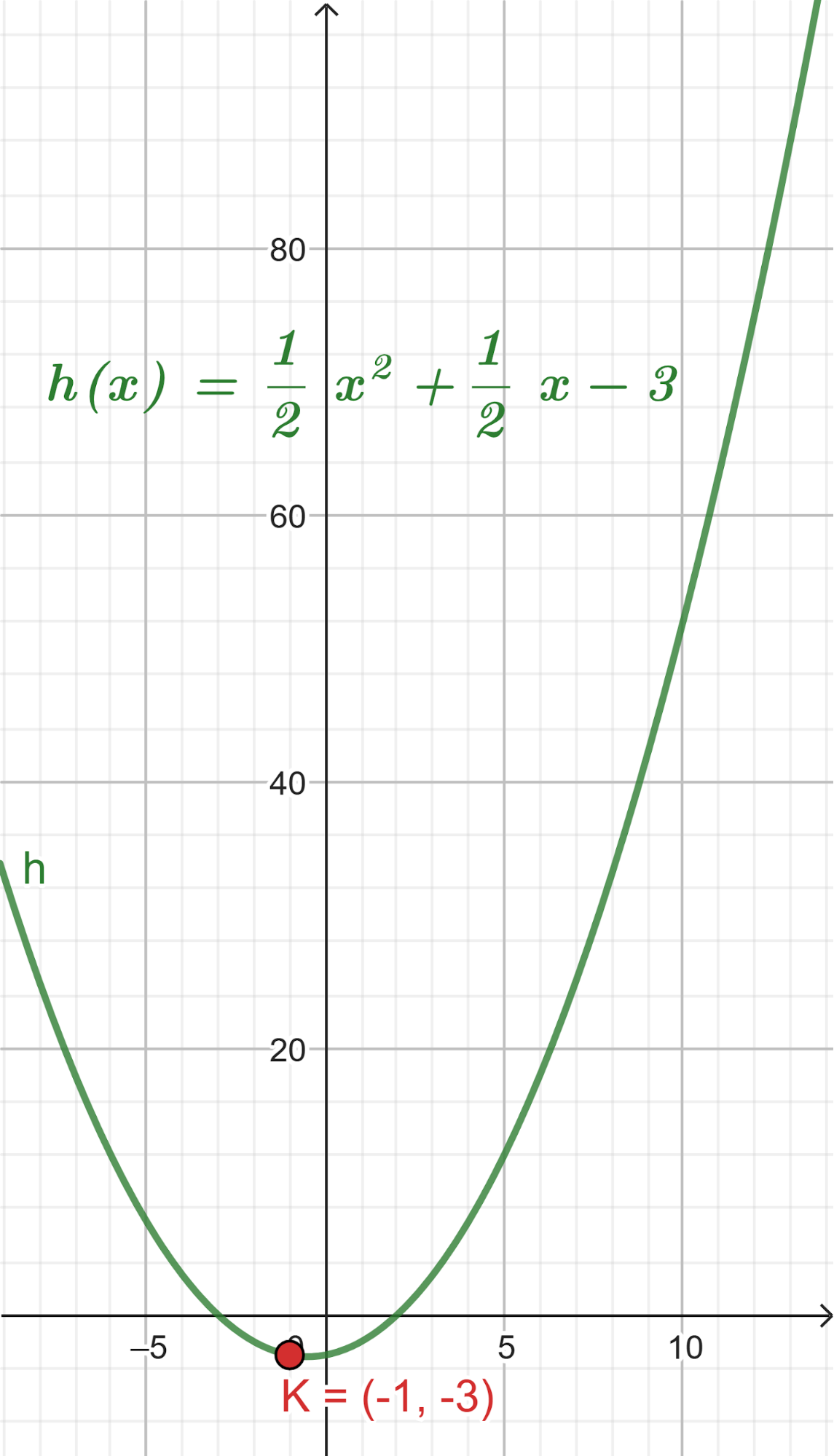
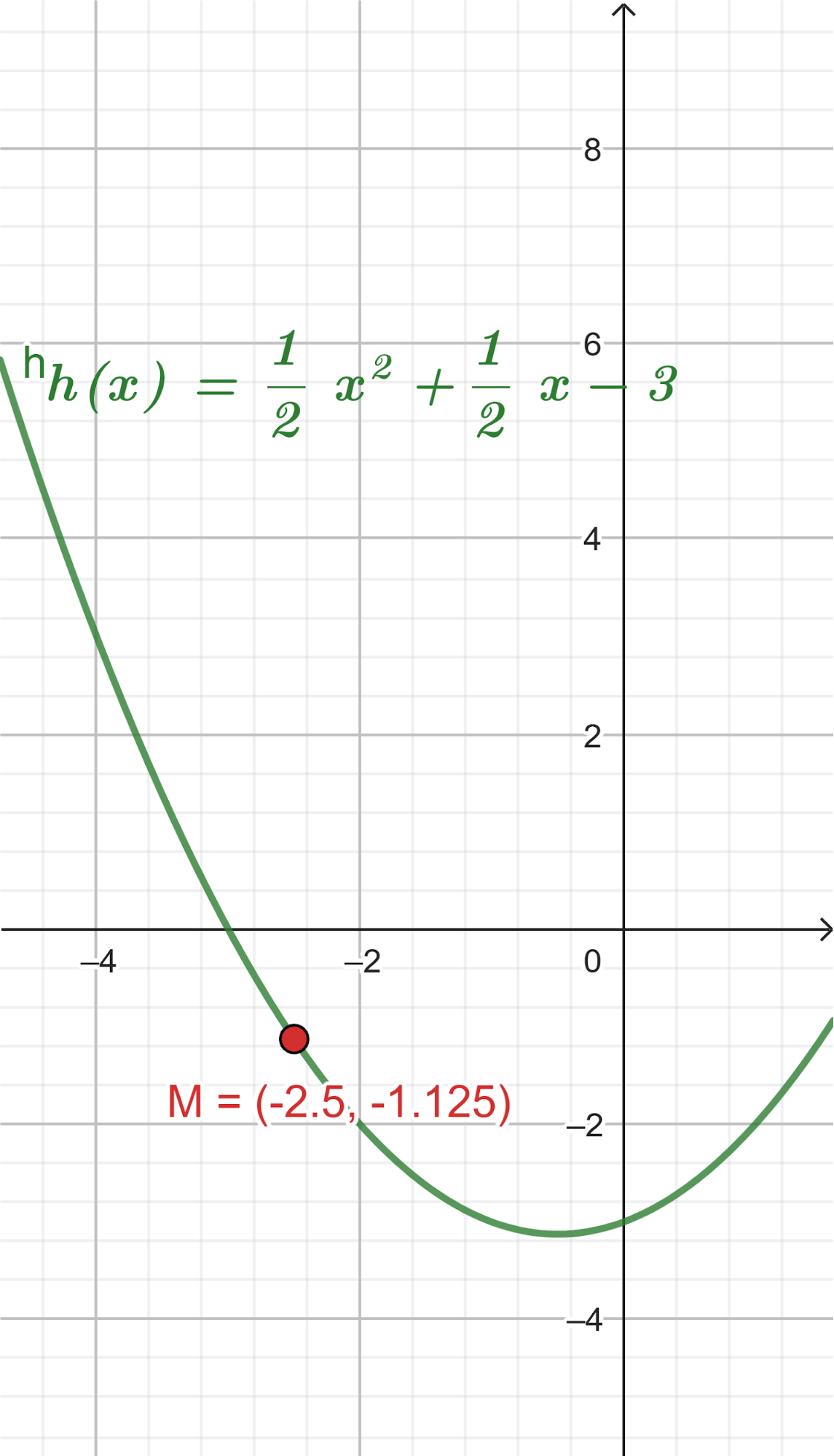
El volúmen máximo lo podemos observar gráficamente en el máximo de la función |
Los invitamos a pensar el problema, hacer un bosquejo de la caja, escribir los datos, plantear fórmulas y comprender las consignas.
2. Solución:
3. El siguiente dibujo con los datos planteados te ayudará a comprender mejor el problema:
4. Funciones Polinómicas:
- Una función polinómica de grado “n” es de la forma:
, siendo , con , con y .
- El dominio de estas funciones son todos los números reales: . Son continuas en
Tipo de Función | Expresión algebraica y Clase de gráfica | Características y Observaciones | Representación gráfica y Tabla de valores | Algunos Ejemplos |
Función constante | Su gráfica es una recta | Su gráfica es una recta horizontal paralela al eje de abscisas (eje X). Si k > 0 entonces la recta está por encima del eje X. Si k < 0 entonces la recta está por debajo del eje X. NOTA: Las rectas verticales, paralelas al eje Y, tienen como expresión algebraica. | ||
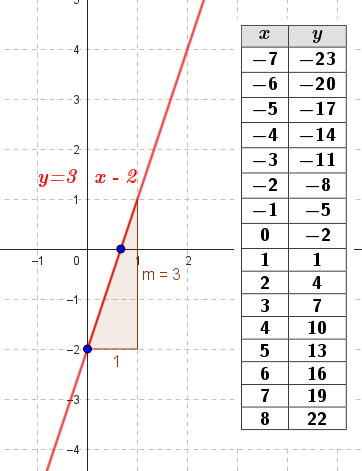
Funciones polinómicas de 1° grado Función afín | Su gráfica es una recta | Su gráfica es una recta oblicua. Queda definida por dos puntos. La pendiente de la recta es “m”. La constante “b” es el punto de corte con el eje Y, pasa por el punto Q(0, b). Cuando mayor es |m| más cerca del eje de ordenadas (eje Y) está y viceversa. Si m > 0 se sitúa en los cuadrantes 1° y 3°. Si m < 0 se sitúa en los cuadrantes 2° y 4°. La inclinación de la recta depende del valor de la pendiente “m”. | ||
Funciones polinómicas de 1° grado Función lineal | Dada Si entonces: Su gráfica es una recta | Se denomina también de proporcionalidad directa. Siempre pasa por el origen de coordenadas O(0, 0). | ||
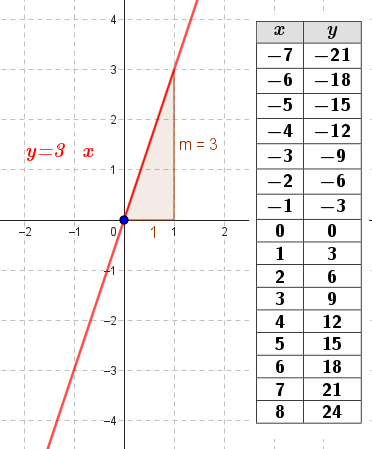
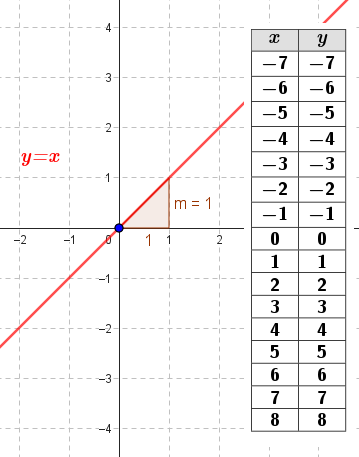
Funciones polinómicas de 1° grado Función identidad | Dada Si y entonces Su gráfica es una recta | Su pendiente es m = 1 Es la bisectriz del 1° y 3° cuadrante y forma un ángulo de 45° con el eje X. Siempre pasa por el origen de coordenadas O(0, 0). Es la bisectriz del 2° y 4° cuadrante. | ||
Funciones polinómicas de 2° grado Función cuadrática | Su gráfica es una curva llamada parábola | Vértice en el punto . Eje de simetría en Puntos de corte con el eje X: Se obtienen resolviendo la ecuación de 2° grado asociada: Punto de corte con el eje Y: Calculamos , siendo Q(0, c). Si a > 0 las ramas parabólicas están hacía arriba (el vértice es un mínimo). Si a < 0 las ramas parabólicas están hacia abajo (el vértice es un máximo). Cuanto mayor sea |a| más próximas están las ramas al eje de ordenadas (eje Y) y viceversa. | ||
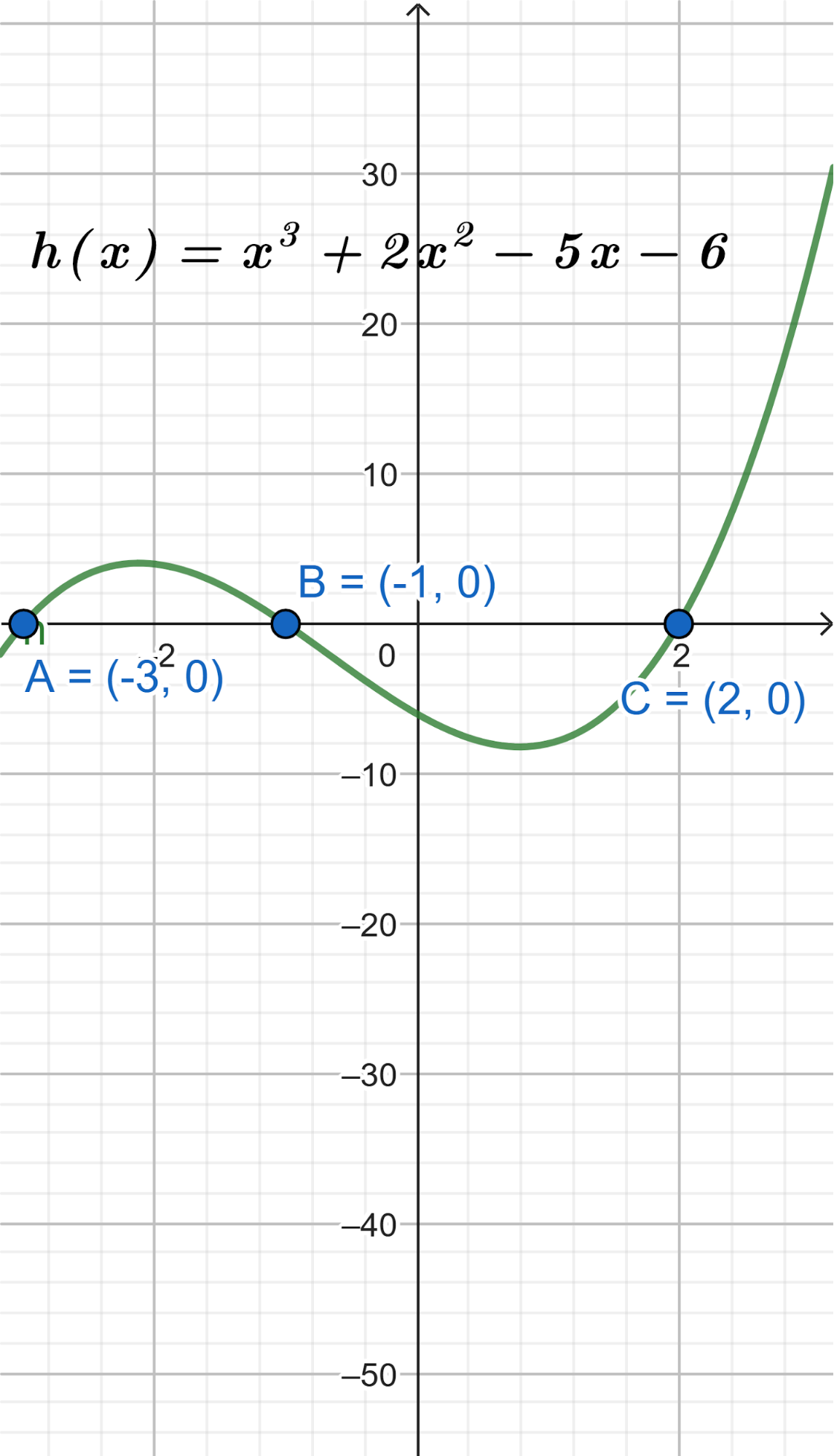
Funciones polinómicas de 3° grado Función cúbica | Su gráfica es una curva Tienen ramas parabólicas | A veces, y con 3 raíces reales, la curva toma las siguientes formas: Si a > 0 la curva tiene forma parecida a una N mayúsculas. Si a < 0 tiene forma parecida a una N mayúsculas invertida. Cuanto mayor es |a| más estilizada es la curva y viceversa. Los puntos de corte con el eje X: Se obtienen resolviendo la ecuación de 3° grado asociada. El punto de corte con el eje Y: Se obtiene calculando , siendo Q(0, d). | ||
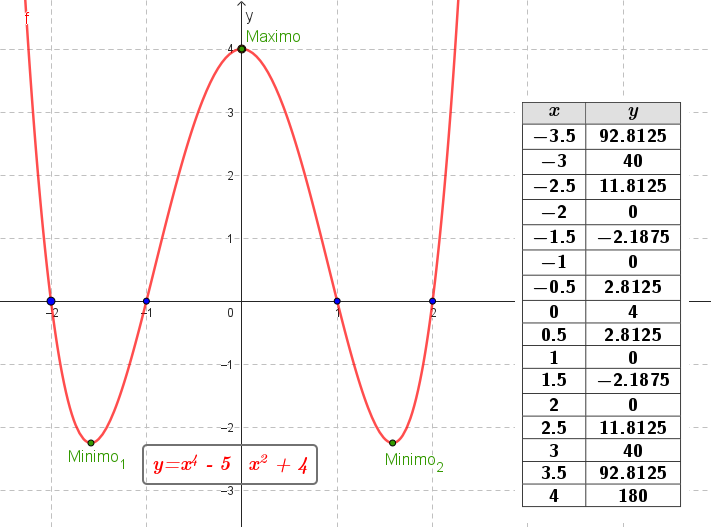
Funciones polinómicas de 4° grado | Su gráfica es una curva Tienen ramas parabólicas | A veces, y con 4 raíces reales, la curva toma las siguientes formas: Si a > 0 la curva tiene una forma parecida a una W mayúsculas. Si a < 0 tiene forma parecida a una M mayúsculas. Cuanto mayor es |a| más estilizada es la curva y viceversa. Los puntos de corte con el eje X: Se obtienen resolviendo la ecuación de 4° grado asociada, igualada a 0. El punto de corte con el eje Y: Se obtiene calculando , siendo . | ||
Funciones polinómicas de grado “n” | Su gráfica es una curva. Se sigue cumpliendo que se dobla una vez menos que el grado de la función. | Las funciones polinómicas no tienen asíntotas, tienen ramas parabólicas. Cuanto mayor es (coeficiente de la x de mayor grado) más estilizada es la curva y viceversa. Los puntos de corte con el eje X: Se obtienen resolviendo la ecuación asociada, igualada a 0. El punto de corte con el eje Y: Es , es decir para calculamos el valor de y. |
5. Para saber más..
- Comportamiento según el coeficiente principal
- Ceros y gráficas de las funciones polinómicas
- Multiplicidad de las raíces
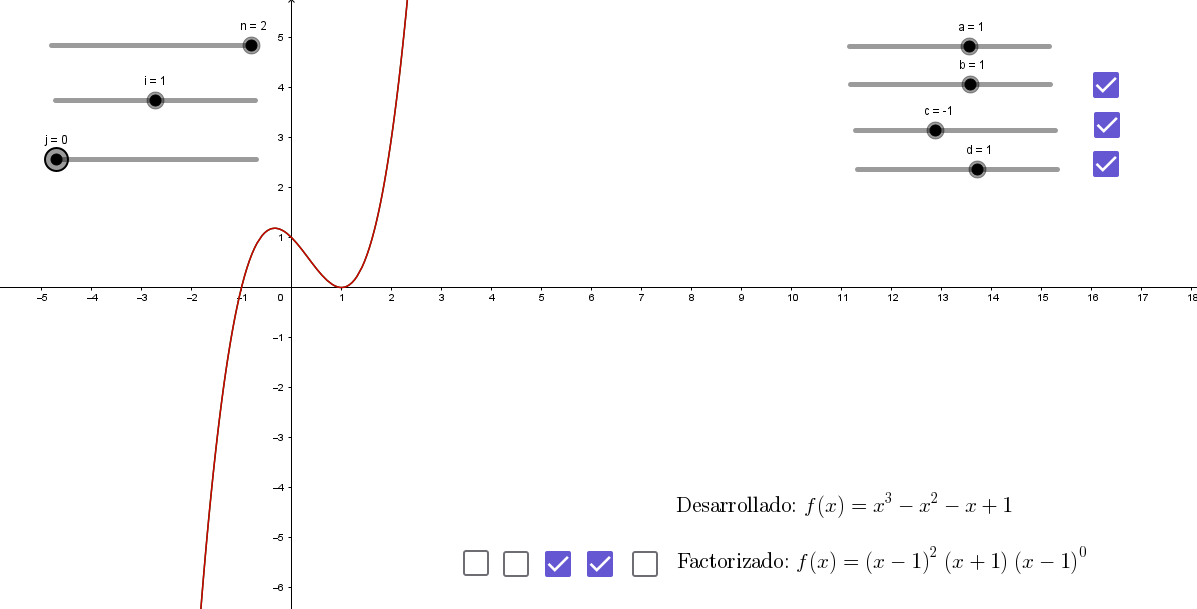
6. GeoGebra:
Sugerimos realizar los siguiente pasos para poder estudiar las funciones polinómicas con esta animación:
- Mover los deslizadores que aparecen en la pantalla principal y anotar qué hace cada uno.
- Tildar un casillero más y luego realizar nuevamente el primer paso.
- Repetir el segundo paso con el tercer casillero.
- Dejar los deslizadores
, 
, 
, 
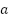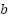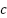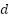fijos y mover solo 
, 
, 
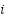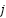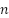. Anotar que sucede. - Dejar los deslizadores 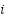, , 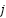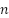fijos y mover los deslizadores 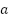, , 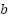, 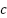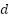. Anotar que sucede.
- Coloca los deslizadores en la posición indicada a continuación y luego responde las siguientes preguntas:
, 
, 
, 
, 
, 
, 
.
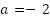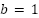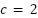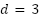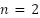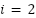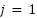- ¿Qué grado tiene el polinomio?
- ¿Cuántas raíces tiene el polinomio? ¿Coincide con el grado? ¿Por qué?
- ¿Cuáles son las raíces?
- ¿Cuál es el orden de multiplicidad de cada raíz?
- ¿Cómo son sus ramas? Describe su comportamiento.
- Prueba los deslizadores en otra posición y responde las mismas preguntas.
- Realiza el paso anterior varias veces.
- Anota todas las conclusiones en tu carpeta y compártelas con tus compañeros.
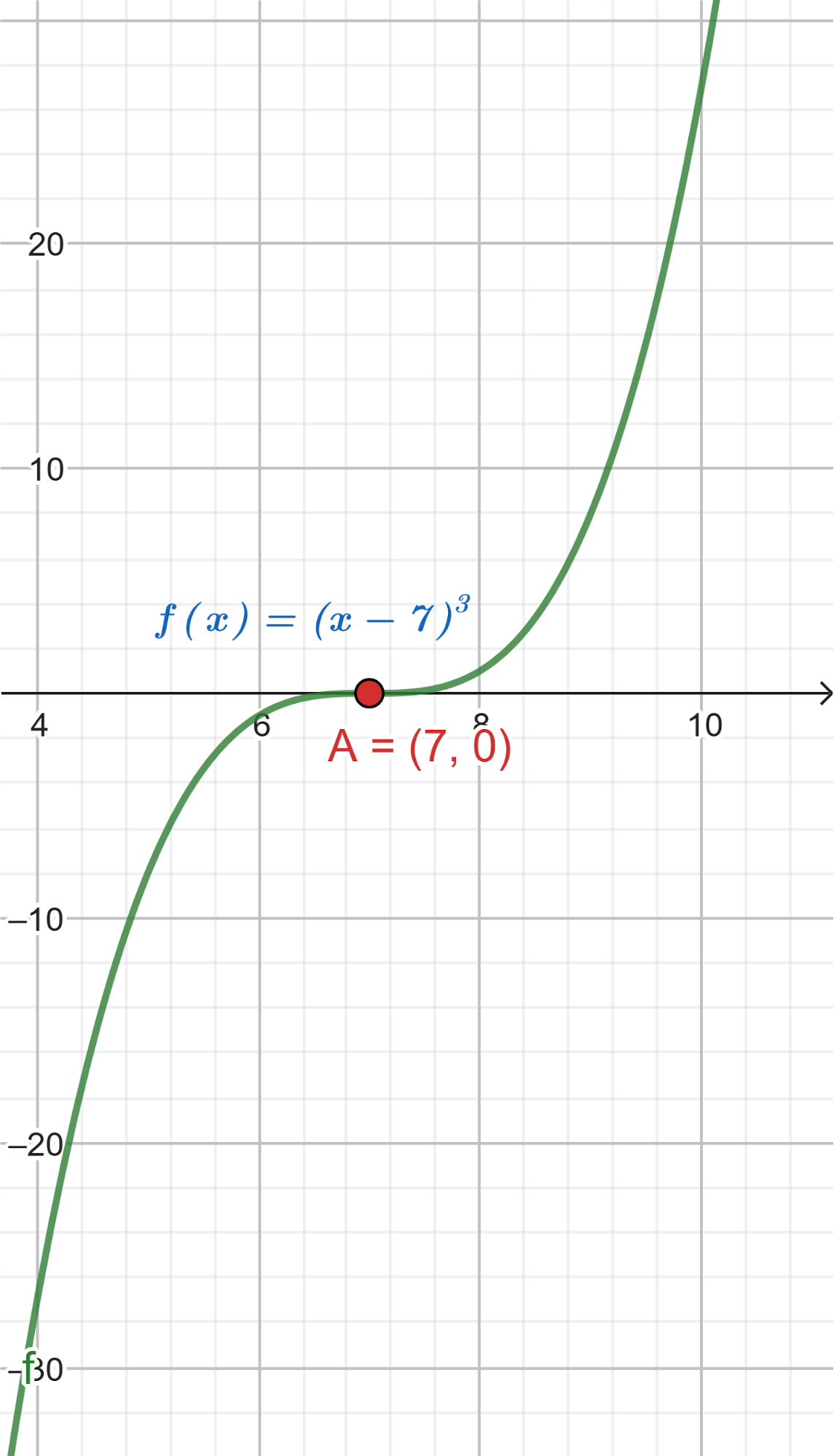
Abajo del cartel con el desarrollo de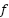 
hay otro cartel oculto. Hay una clave al costado, armada en términos de casillas de control. (Clave 001100).
7. Ejercicios indicados por el docente.
Práctica:
Problema 1 Lean el siguiente recuadro:
En estas últimas dos unidades hemos estudiado en detalle las funciones lineales, que responden a fórmulas del tipo: y las funciones cuadráticas, que responden a fórmulas del tipo: Debido al valor del máximo exponente que aparece en las variables en cada una de estas funciones, se dice que las lineales son de grado 1 y las cuadráticas son de grado 2. Siguiendo de la misma manera, se puede pensar en una familia más general de funciones donde los grados son más altos. Como irán apareciendo más términos y sería incómodo ir eligiendo distintas letras para nombrar a cada coeficiente, comenzaremos a nombrarlos de otra manera: será el término independiente, el coeficiente lineal (La pendiente m de la recta), el coeficiente cuadrático y así sucesivamente. Con esta escritura las fórmulas quedarían así:
Todas estas funciones se llaman Funciones Polinómicas. Este problema nos servirá para investigar propiedades de los gráficos de distintas funciones polinómicas, en relación a sus fórmulas y también distintas formas equivalentes de escribir sus fórmulas. |
Abran el archivo FuncionesPolinomicas.ggb. La idea es explorar y construir entre todos observaciones y afirmaciones que podamos comprobar o descartar para ir conociendo estas funciones.
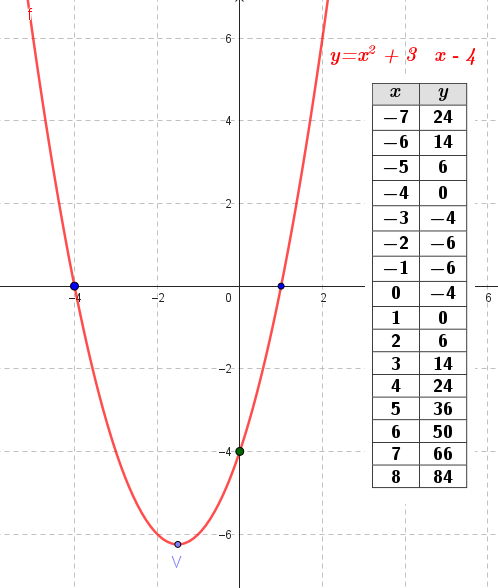
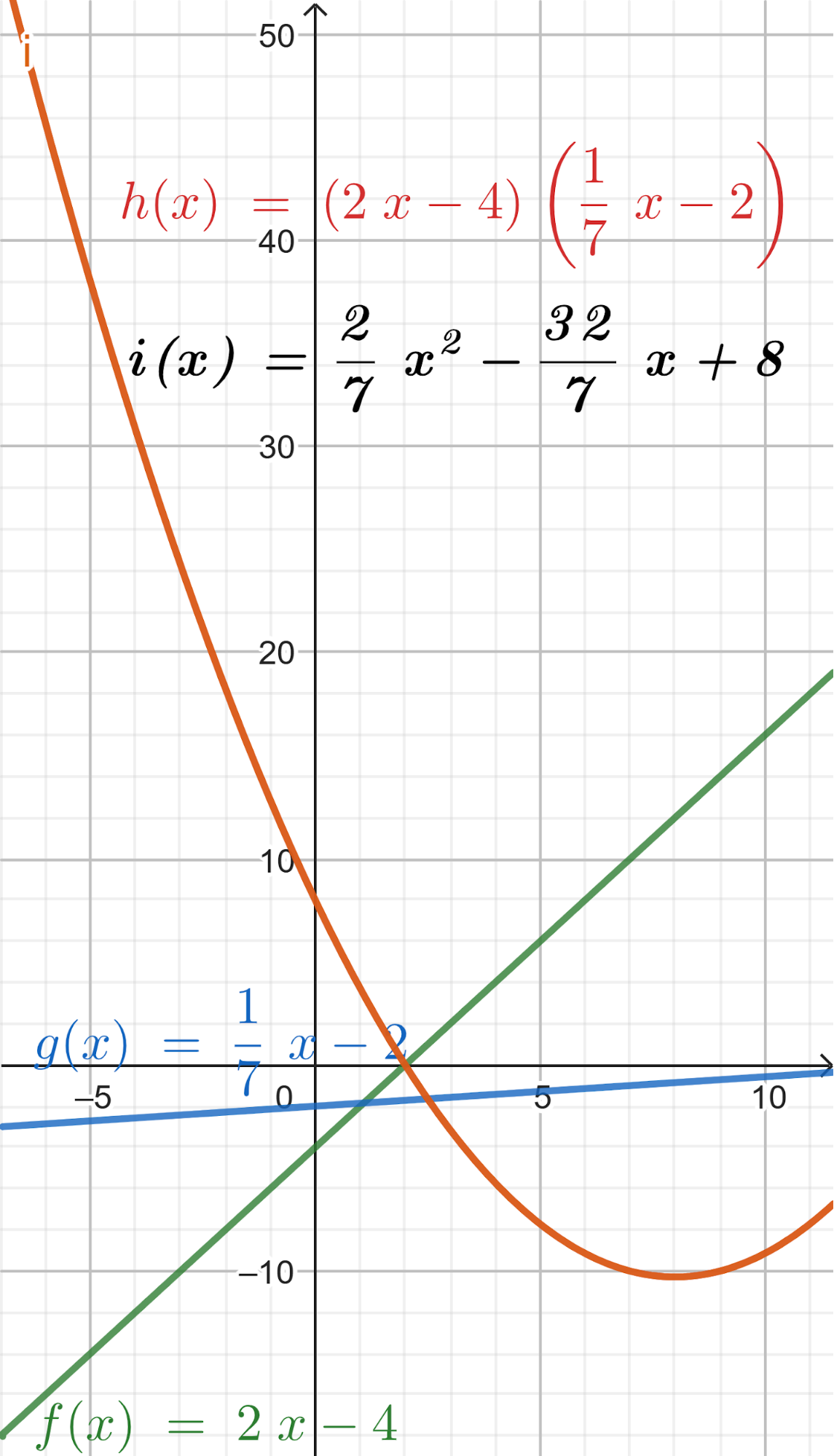
Problema 2 Utilicen las conclusiones del Problema 1 para decidir cuál de los gráficos corresponde a cada una de las funciones polinómicas de grado 2 dadas.
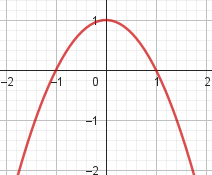
No, porque es de grado 3 y tiene 3 raíces: | No, porque sus raíces son 1 y -1: |
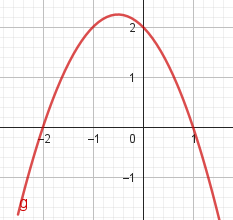
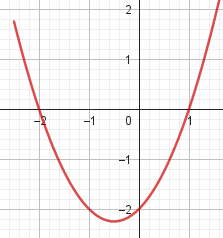
Este gráfico se corresponde con g(x) ya que es de grado 2, sus raíces son -2 y 1 y la concavidad es negativa: | Este gráfico se corresponde con f(x) ya que es de grado 2, sus raíces son -2 y 1 y la concavidad es positiva: |
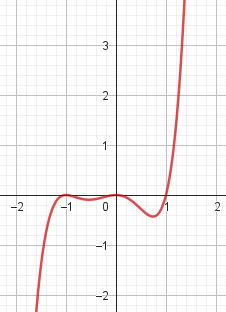
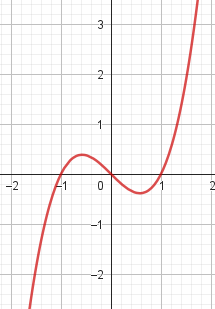
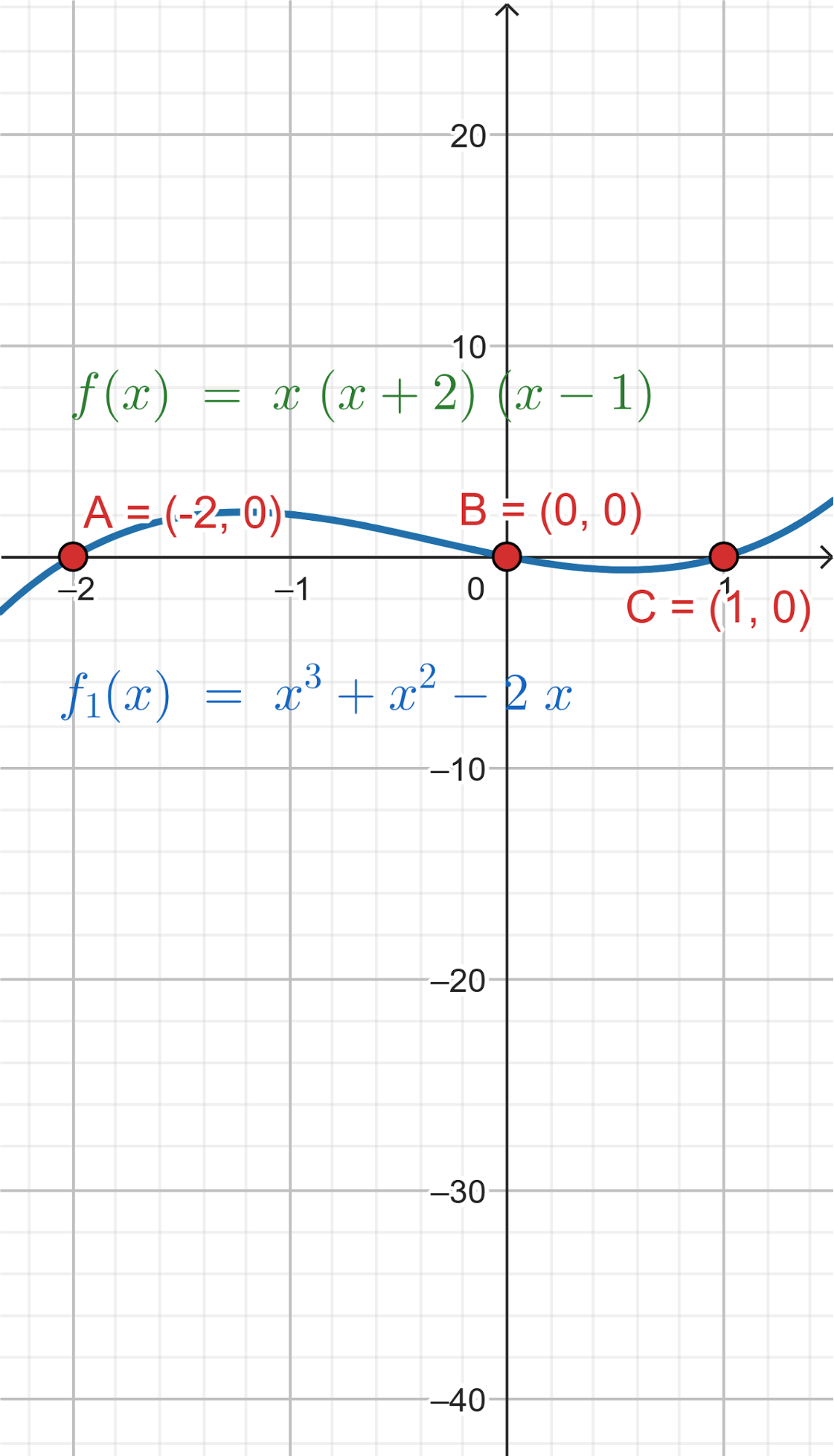
Problema 3 Utilicen las conclusiones del Problema 1 para decidir cuál de los gráficos corresponde a cada una de las funciones polinómicas dadas.
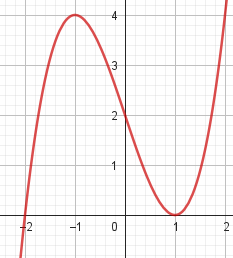
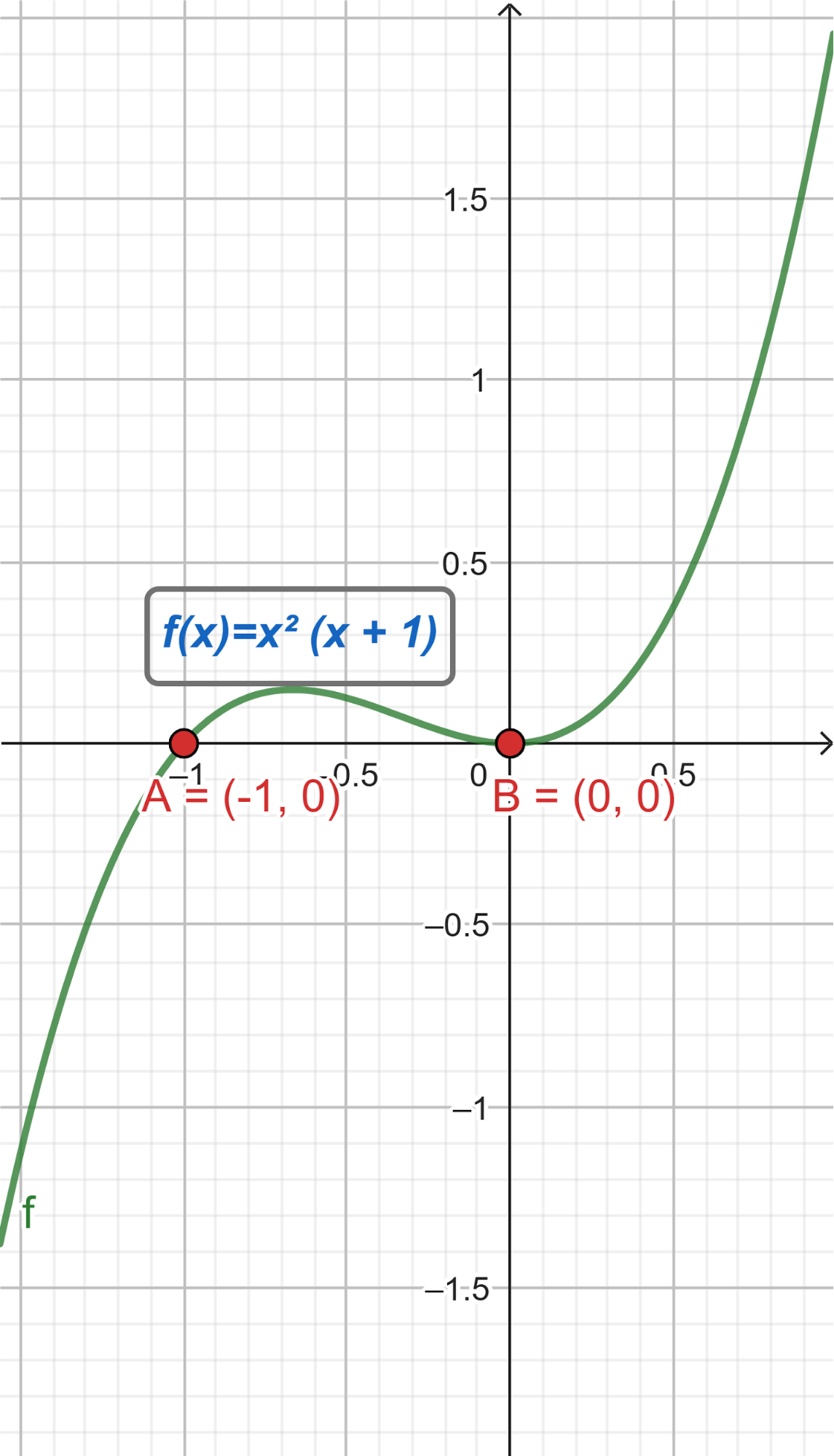
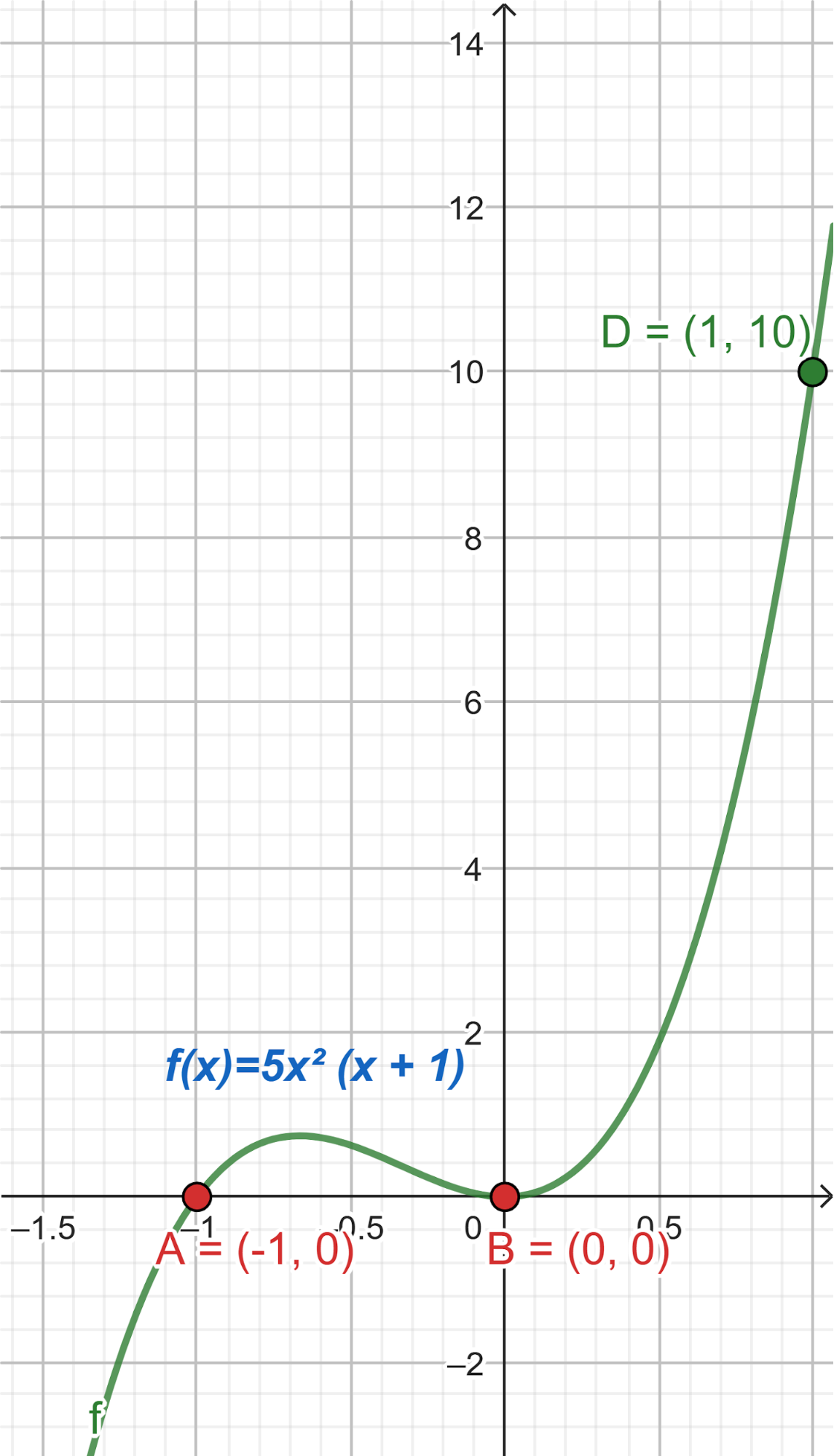
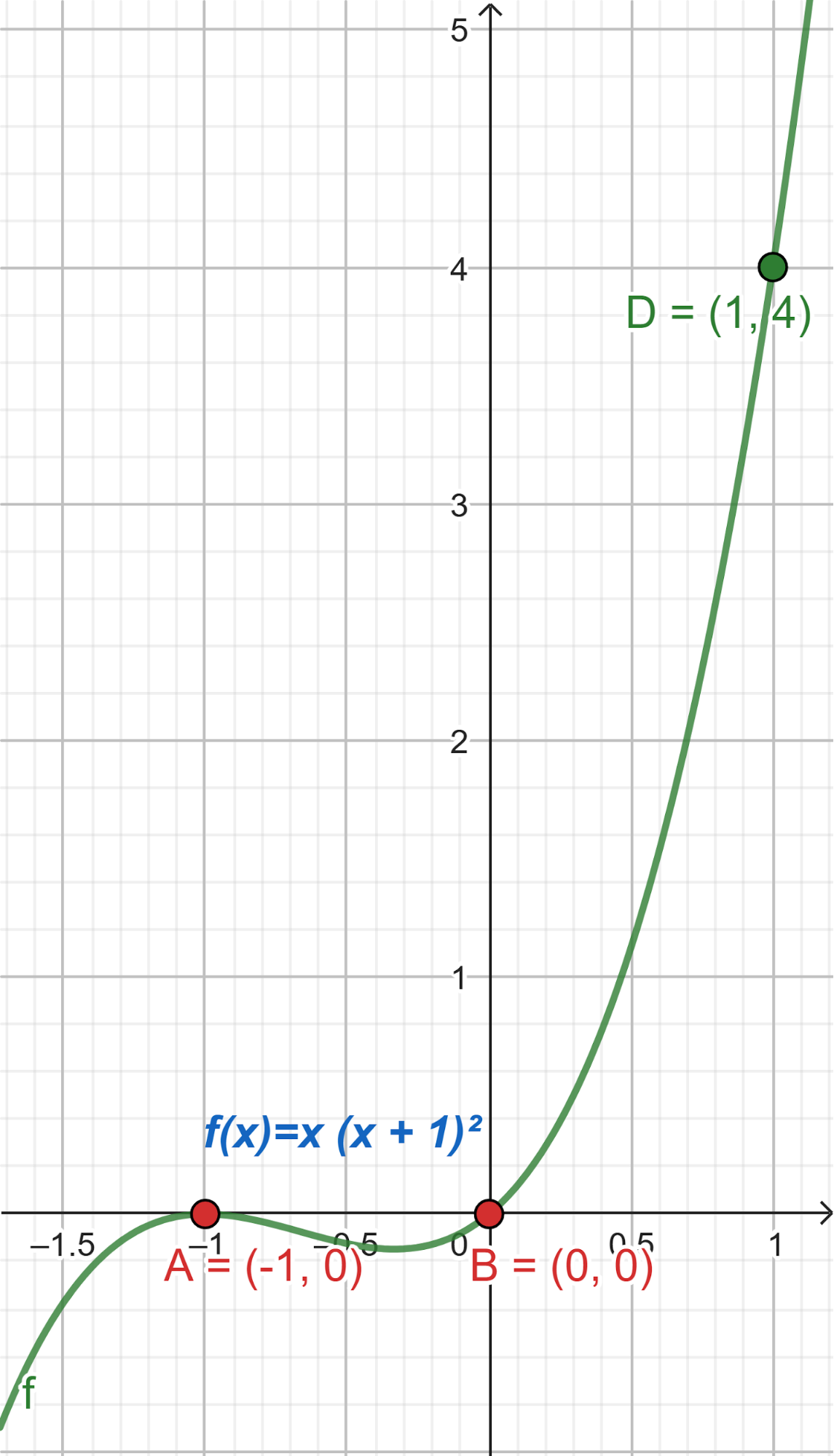
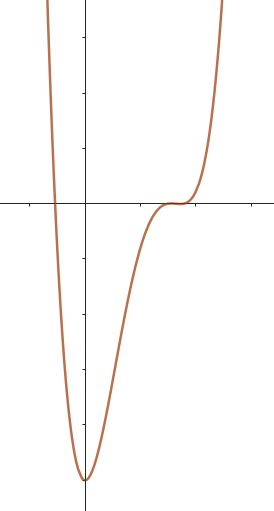
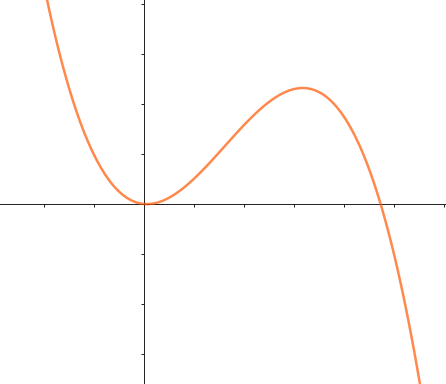
Este gráfico se corresponde con g(x) ya que es de grado 5, sus raíces son -1(multiplicidad=2), 0(multiplicidad=2) y 1, su coeficiente principal es positivo: Factorizada: | Este gráfico se corresponde con f(x) ya que es de grado 3, sus raíces son -1, 0 y 1, su coeficiente principal es positivo: Factorizada: |
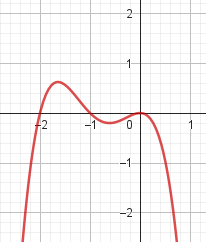
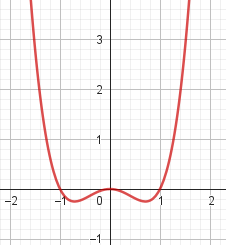
No, porque su coeficiente principal es negativo: Factorizada: | No, porque es de grado 4 y tiene la raíz 0 con multiplicidad=2: Factorizada: |
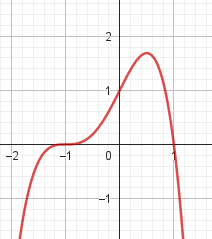
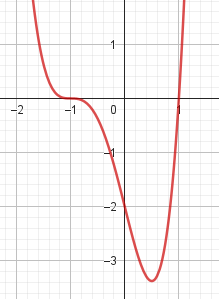
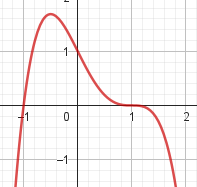
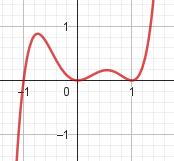
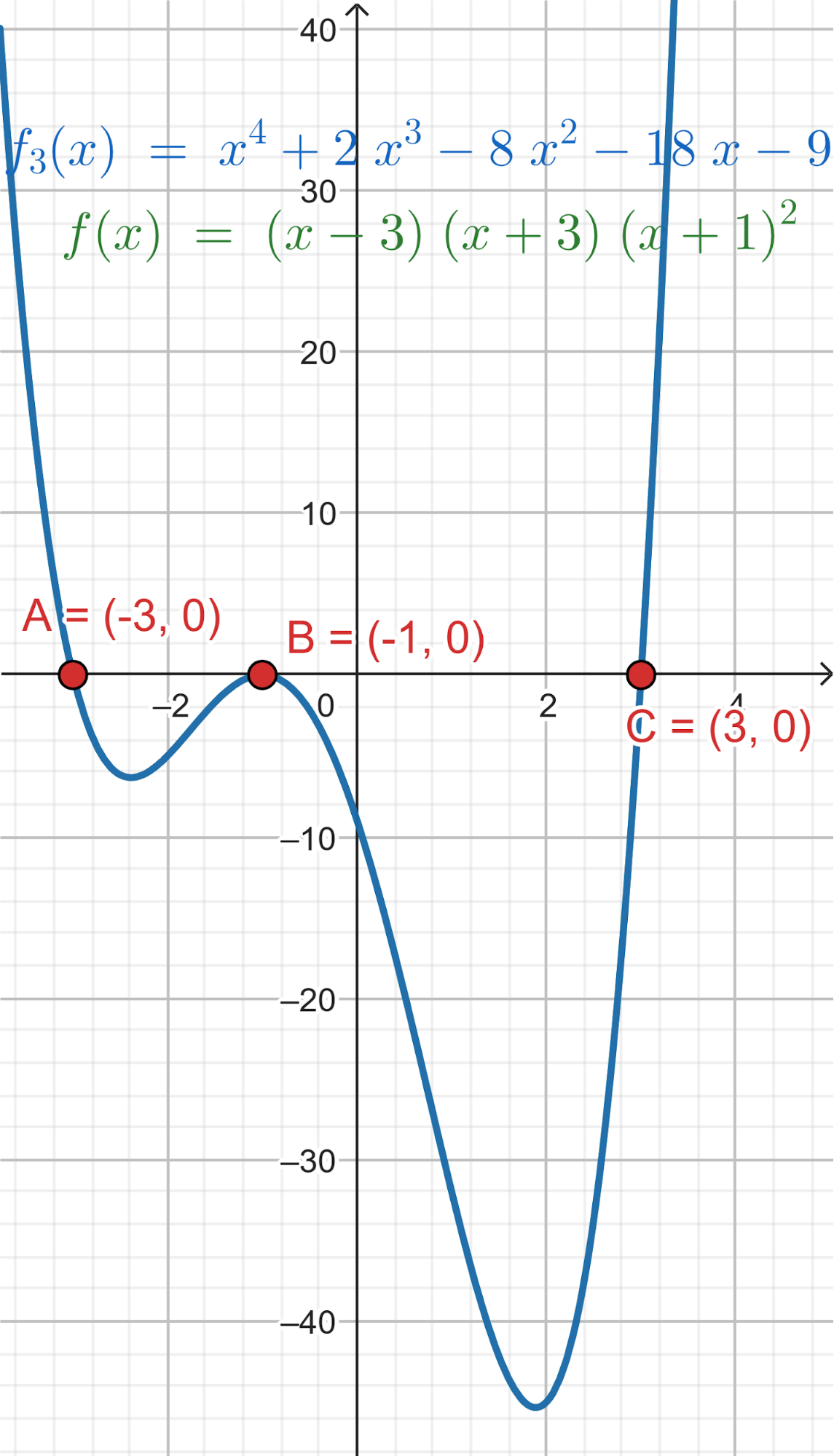
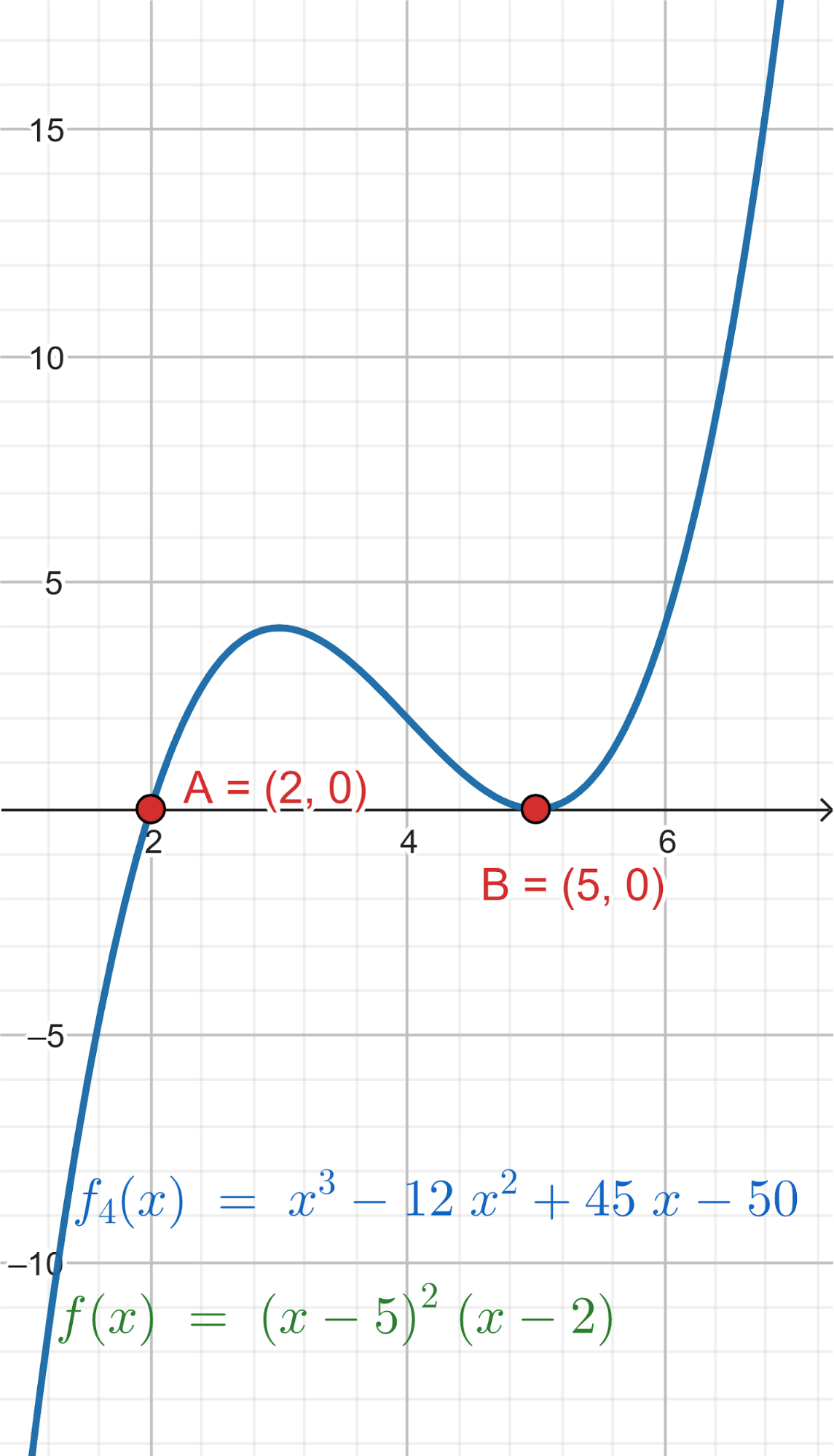
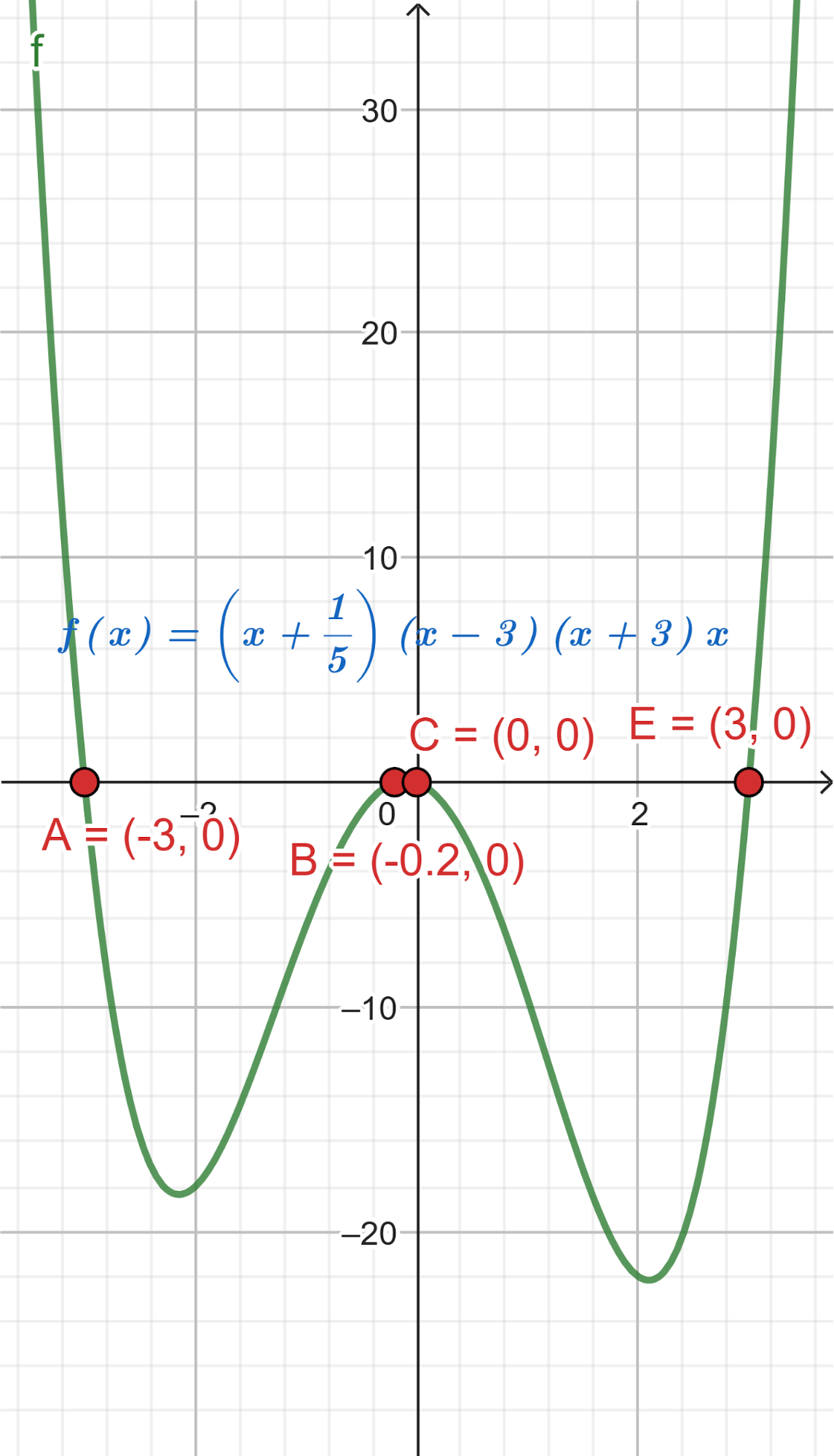
Problema 4 La misma consigna que en los problemas anteriores, para las siguientes funciones y gráficos:.
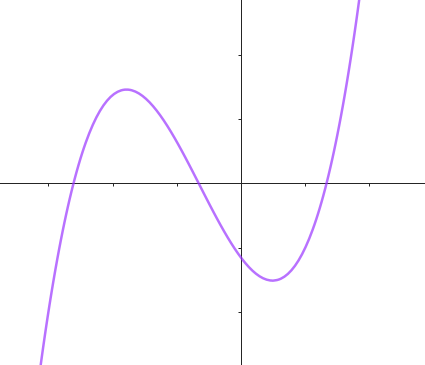
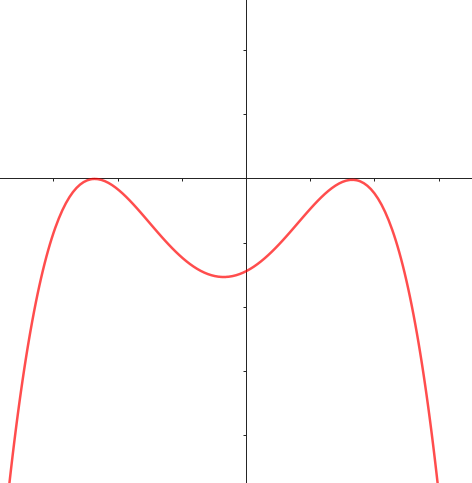
Este gráfico se corresponde con f(x) ya que sus raíces son -1 (multiplicidad=3) y 1, su coeficiente principal es negativo: Desarrollada: | No, porque su coeficiente principal es 2: Desarrollada: |
No, porque su coeficiente principal es negativo, tiene raíces -1 y 1 (multiplicidad=3): Desarrollada: | Este gráfico se corresponde con g(x) ya que su coeficiente principal es positivo, sus raíces son -1, 0 (multiplicidad = 2) y 1 (multiplicidad = 2): Desarrollada: |
Problema 5
- Verifiquen sus respuestas del Problema 4 ingresando en la Barra de Entrada de GeoGebra las funciones y .
Solución:
Factorizada: Desarrollada: | Factorizada: Desarrollada: |
- Investiguen el comando en Inglés para las funciones del ítem anterior. ¿Cómo funciona este comando?¿Cómo harían calculando con lápiz y papel lo que hace el comando?.
Solución:
El comando recibe la función y devuelve la forma Desarrollada o Polinómica. Nosotros debemos aplicar la Propiedad Distributiva y dependiendo el caso el Binomio Cuadrado o Cúbico.
- Binomio al Cuadrado:
- Binomio al Cubo:
Problema 6
- Desarrollen calculando con lápiz y papel las siguientes funciones polinómicas:
Solución:
Solución:
Solución:
Solución:
- Observen las fórmulas de dadas en el ítem anterior y las versiones desarrolladas obtenidas. ¿A partir de cuál de esas versiones les resultaría más fácil dibujar un gráfico aproximado de las funciones?.
Solución:
Resulta más simple dibujar la función con la forma Factorizada ya que nos indica raíces y multiplicidad, además de coeficiente principal. La forma Polinómica o Desarrollada nos indica el coeficiente principal, el corte de ordenada, el corrimiento lateral, y las concavidades, pero se complica más al momento de realizar el gráfico.
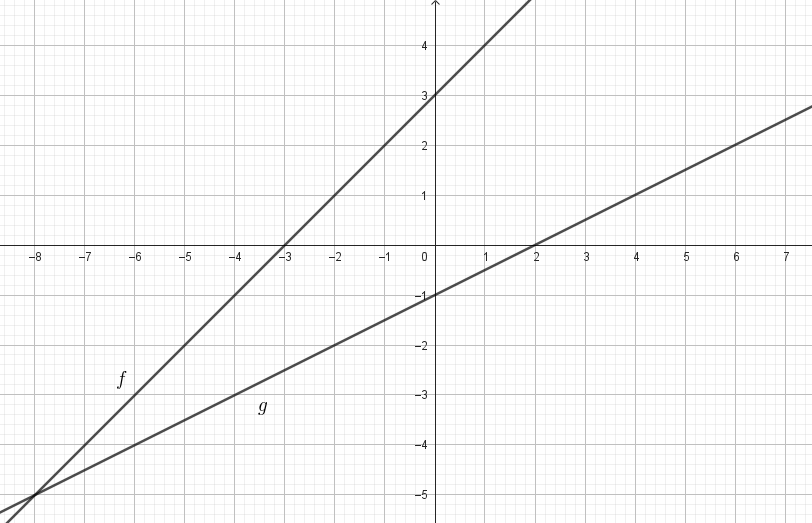
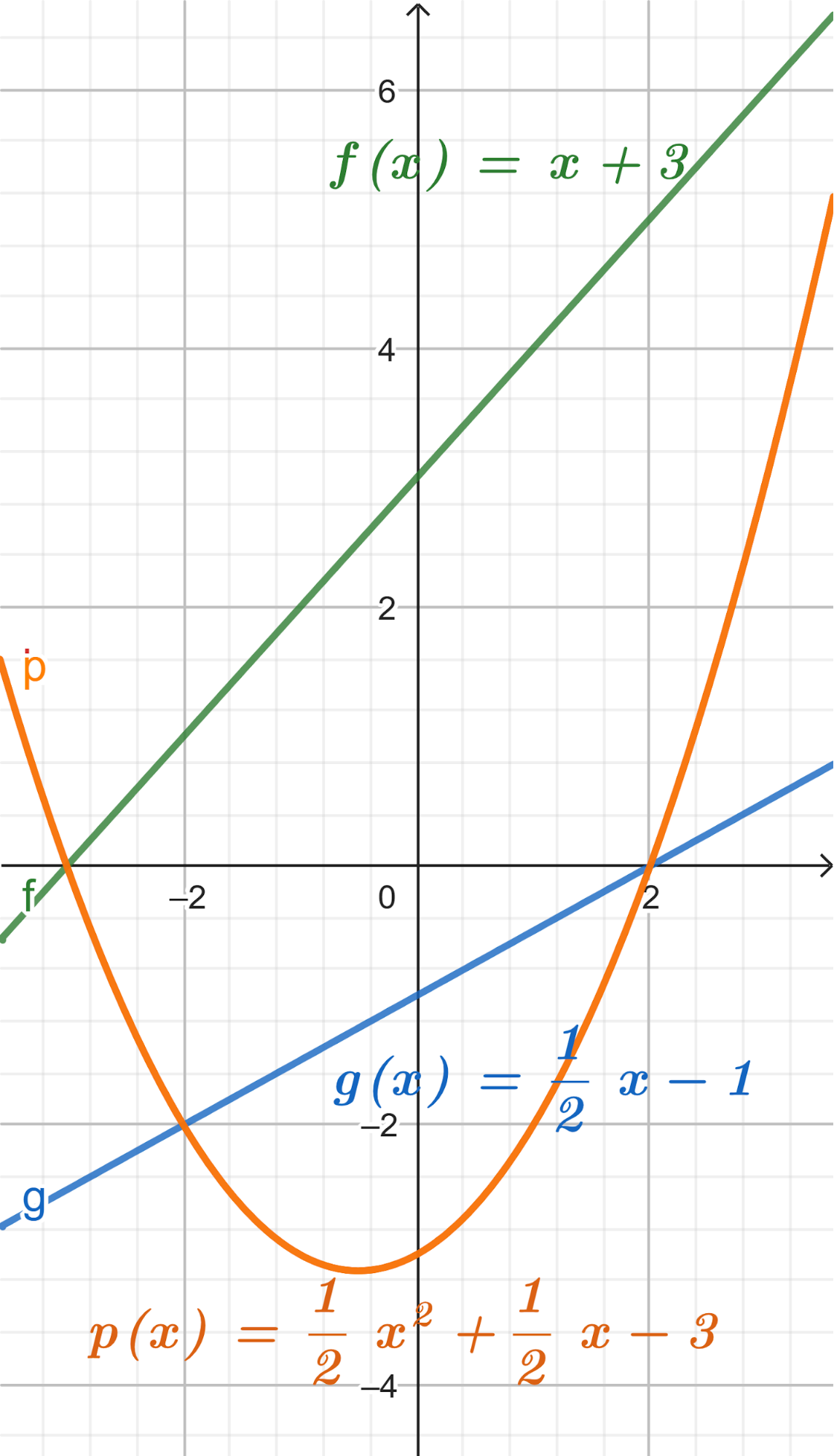
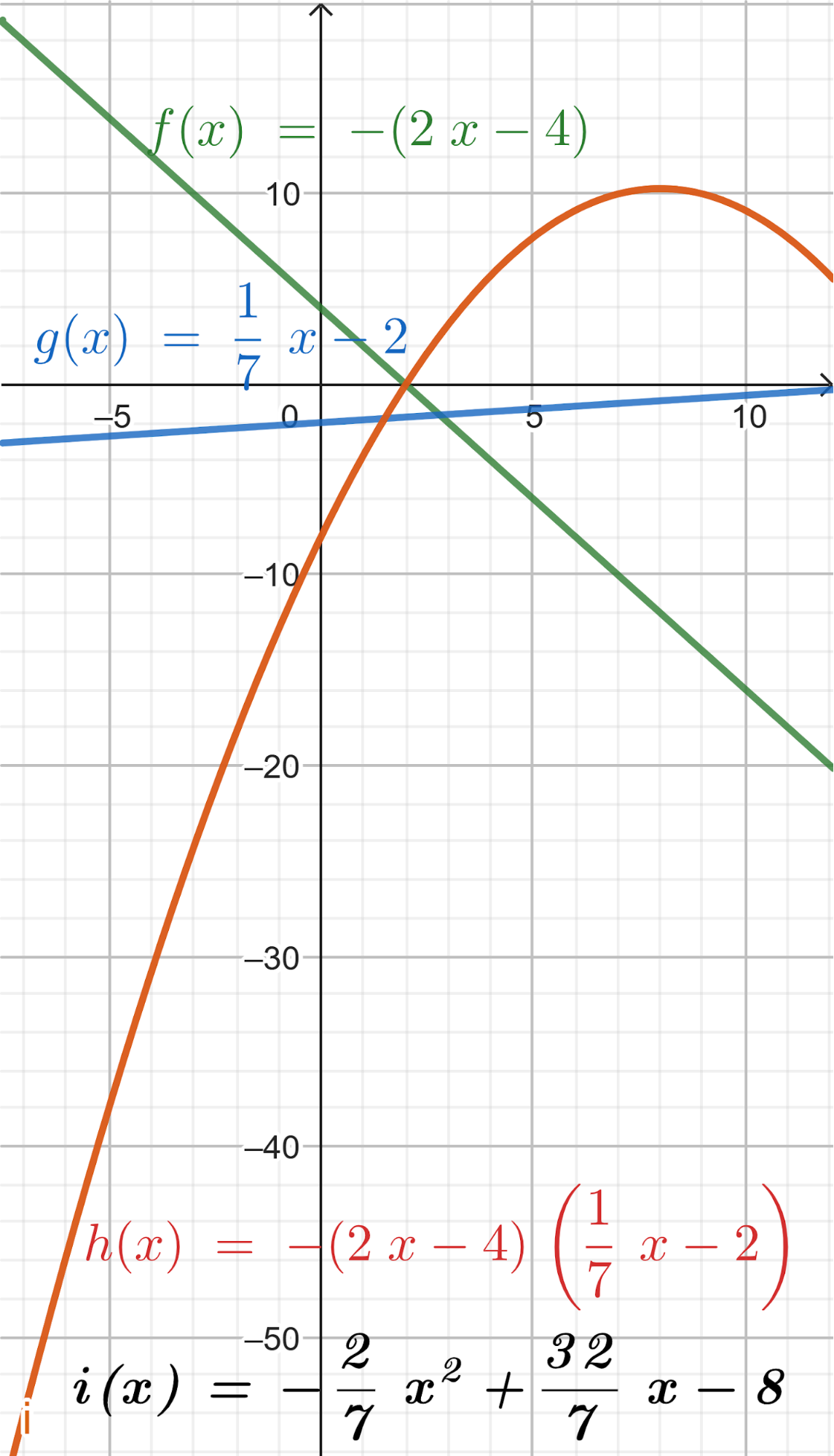
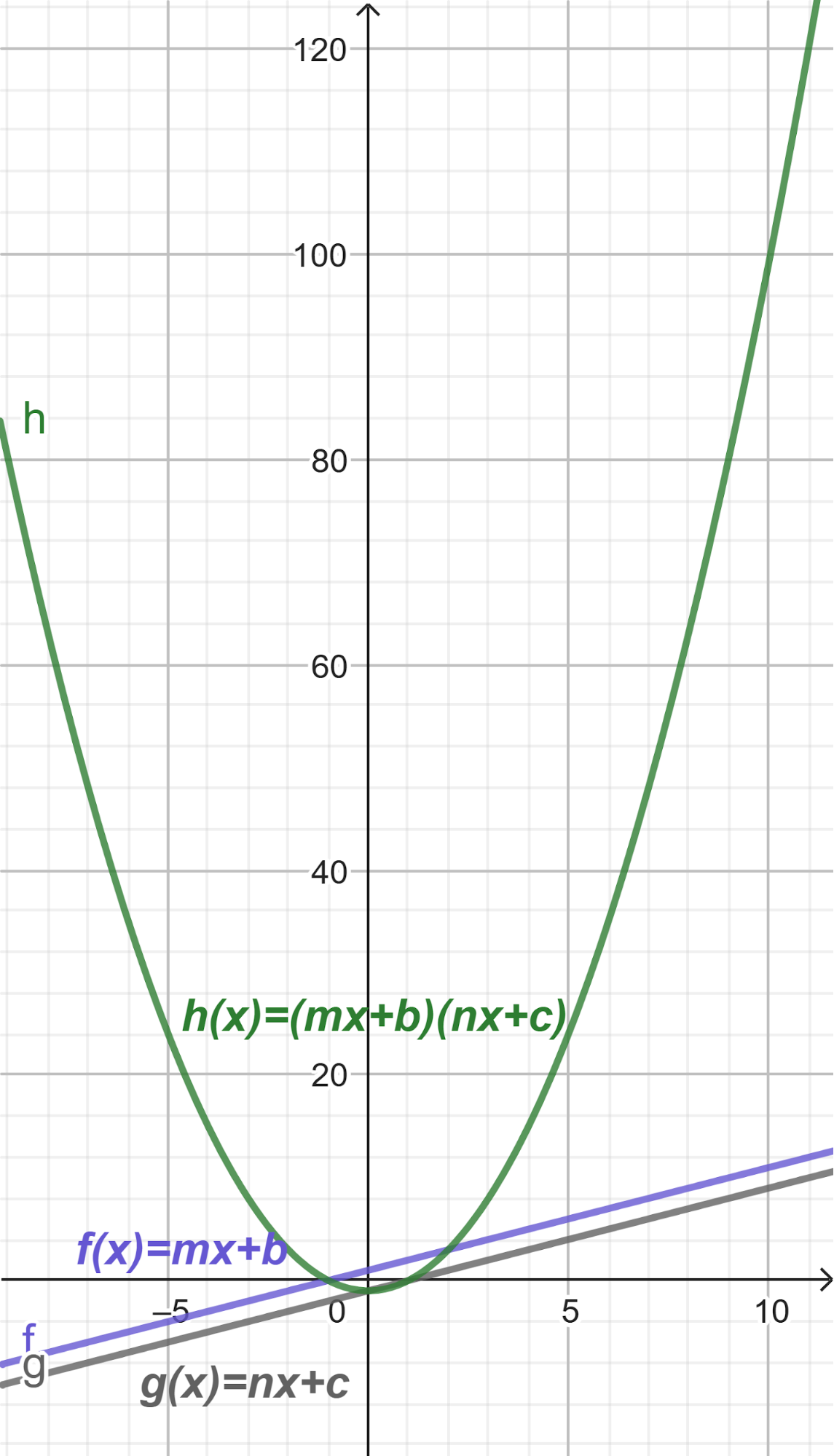
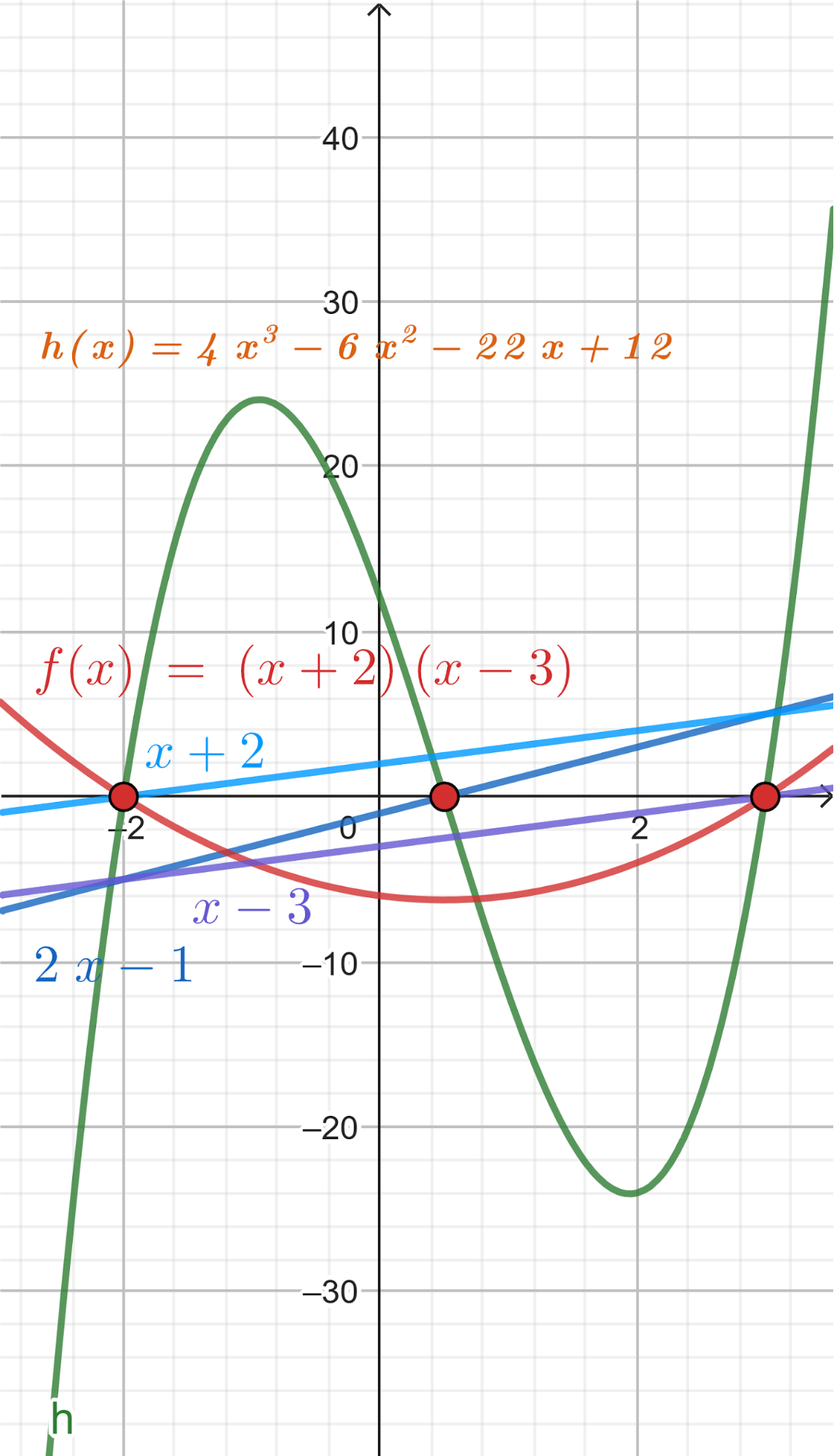
Problema 7 Sean y dos funciones lineales. Definimos la función de la siguiente manera: Para cada valor de , . A partir de los gráficos de y de que se dan a continuación, les proponemos:
Solución: Siendo con corte de ordenada su raíz hallamos su pendiente: Quedando: Siendo con corte de ordenada su raíz hallamos su pendiente: Quedando: Por lo tanto: |
- Calculen el valor de en cada caso:
Solución:
Solución:
Solución:
Solución:
Solución:
Solución:
Solución:
Solución:
- Decidan si es negativa, positiva o cero:
Solución:
Es Positiva.
Solución:
Es Positiva.
Solución:
Es Negativa.
Solución:
Es Positiva.
Solución:
Es Negativa.
- Propongan un gráfico aproximado de .
Problema 8
- Propongan, si es posible, dos funciones lineales cuyo producto sea una función cuadrática que tenga mínimo y otras dos para que la función cuadrática tenga máximo. Si no hay, justifiquen la respuesta.
Solución:
y
- Ídem con el máximo:
Solución:
y
Problema 9 Lean las siguientes preguntas, escriban sus respuestas en el cuaderno y luego compartan lo que escribieron:
- ¿Es cierto que siempre que multiplicamos dos funciones cuyos gráficos son rectas obtenemos una función cuyo gráfico es una parábola?.
Si, teniendo dos funciones lineales con pendiente distinta de cero:
y entonces
Aplicamos Propiedad Distributiva.
Factor Común en segundo y tercer término
La cuál tiene forma de una función cuadrática cuya gráfica es una parábola.
Siendo:
- Coeficiente principal
- Coeficiente lineal.
- Término independiente.
- ¿Cómo obtenemos los ceros, el conjunto de positividad y el conjunto de negatividad de la parábola a partir de los gráficos de las rectas?.
Solución:
Los ceros los obtenemos de las raíces de cada recta, el conjunto positividad y/o negatividad evaluando la parábola x entre las raíces .
- ¿Es cierto que toda función cuadrática puede ser escrita como el producto de dos funciones lineales?.
Solución:
Si, como se demostró en la parte a del problema.
- ¿Cómo deben ser las rectas para que su producto sea una parábola que tenga máximo? ¿Y mínimo?.
Solución:
Para que tenga máximo deben tener diferentes signos en su pendiente, e igual signo para que tenga mínimo.
- ¿Cómo deben ser las rectas para que su producto sea una parábola con un cero doble? ¿Y con dos ceros simples?.
Solución:
Para que su producto sea una parábola con un cero doble, debe ser la misma recta, o tener el corte de ordenada y pendiente con misma magnitud y signos opuestos osea que compartan la misma raíz, de otra forma tendrá ceros simples o no tendrá raíces reales.
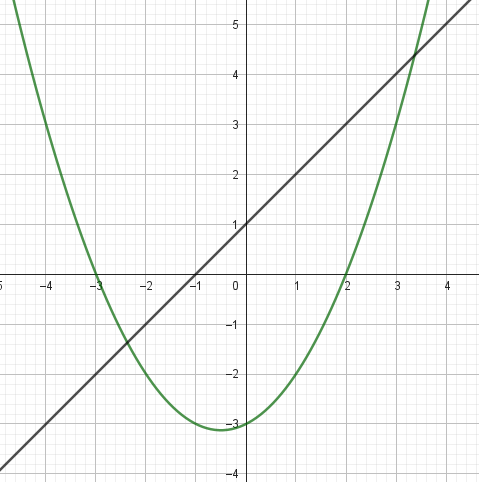
Problema 10 A continuación se dan los gráficos de y de .
Sea :
Solución: Tomando como la recta, y a la parábola, tenemos que: Y: Por lo cual: Desarrollada: |
- Calculen:
Solución:
Solución:
Solución:
Solución:
Solución:
Solución:
- Decidan si es positiva, negativa o cero:
Solución:
Positiva.
Solución:
Negativa.
Solución:
Negativa.
Solución:
Negativa.
Solución:
Positiva.
Solución:
Positiva.
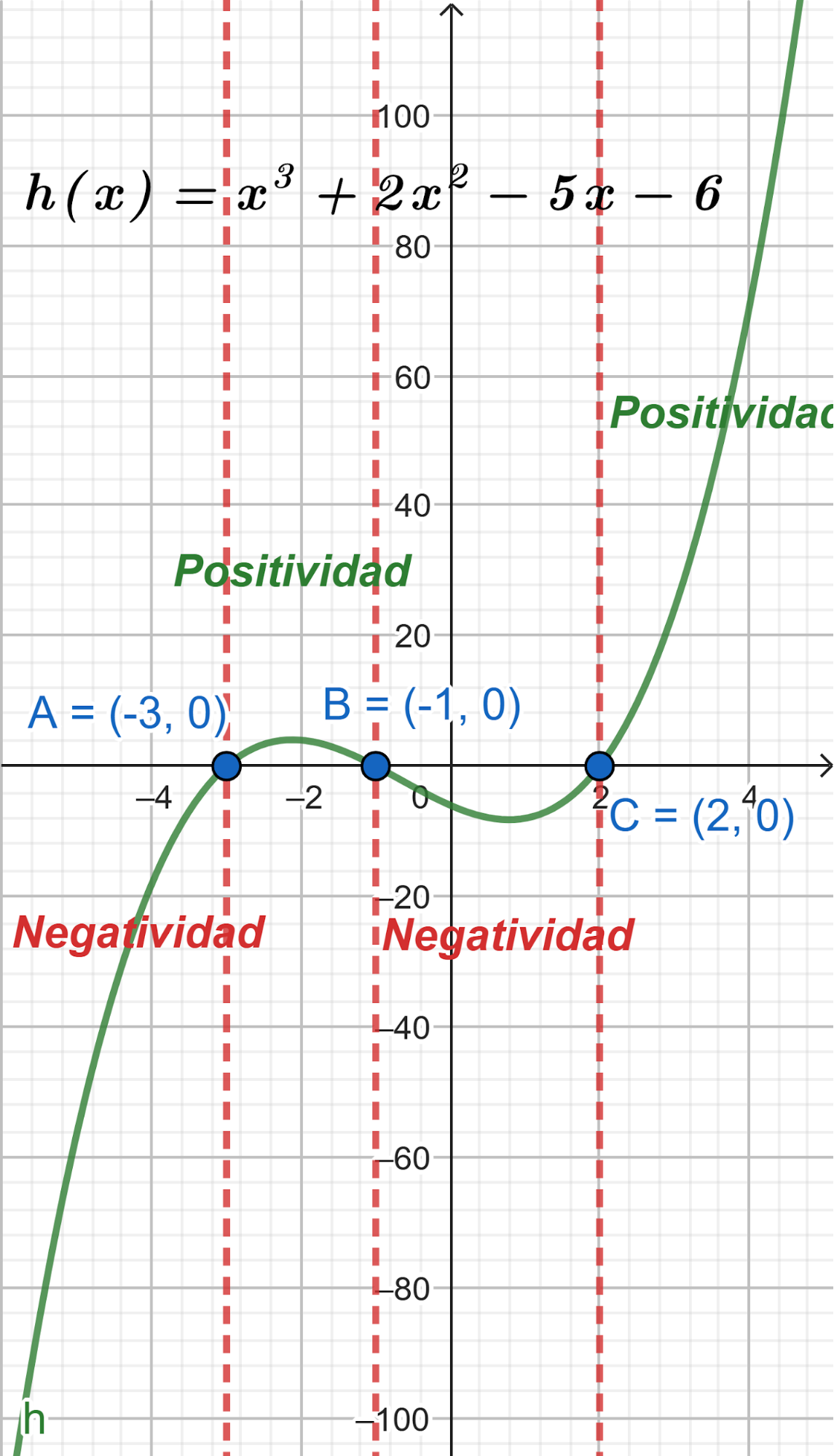
- Indiquen ceros, el conjunto de positividad y el de negatividad.
Solución:
Ceros: (-3; -1; 2)
Conjunto positividad: (; )
Conjunto negatividad: (; )
- Grafiquen aproximadamente.
Problema 11 En cada caso, halle si existe, la fórmula de una función cúbica que verifique lo pedido. Si le parece que no existe, explique por qué:
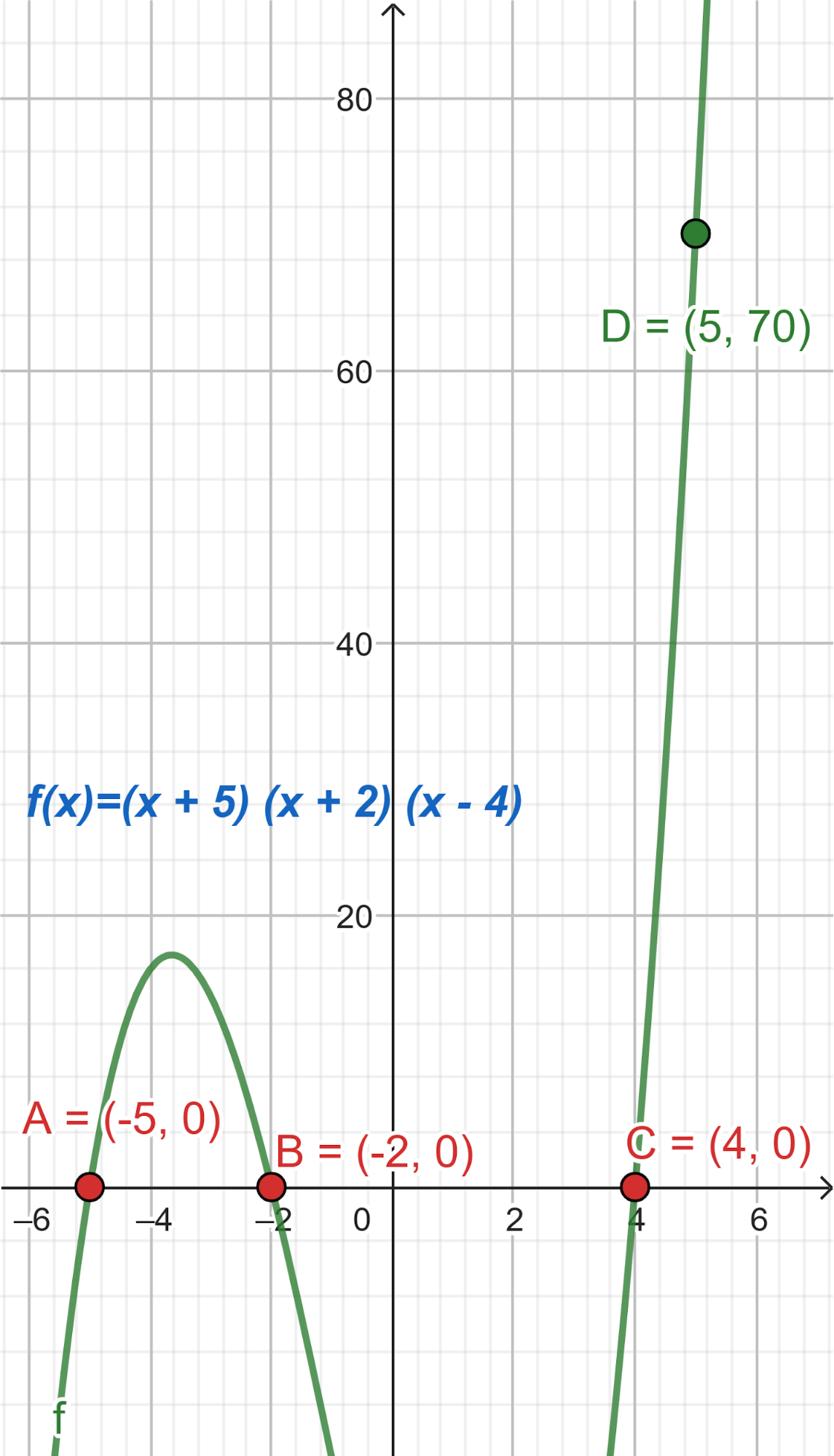
- Las raíces son -5, -2, 4 y toma valores negativos para mayores que 4.
Solución:
Evaluamos en :
Positiva para
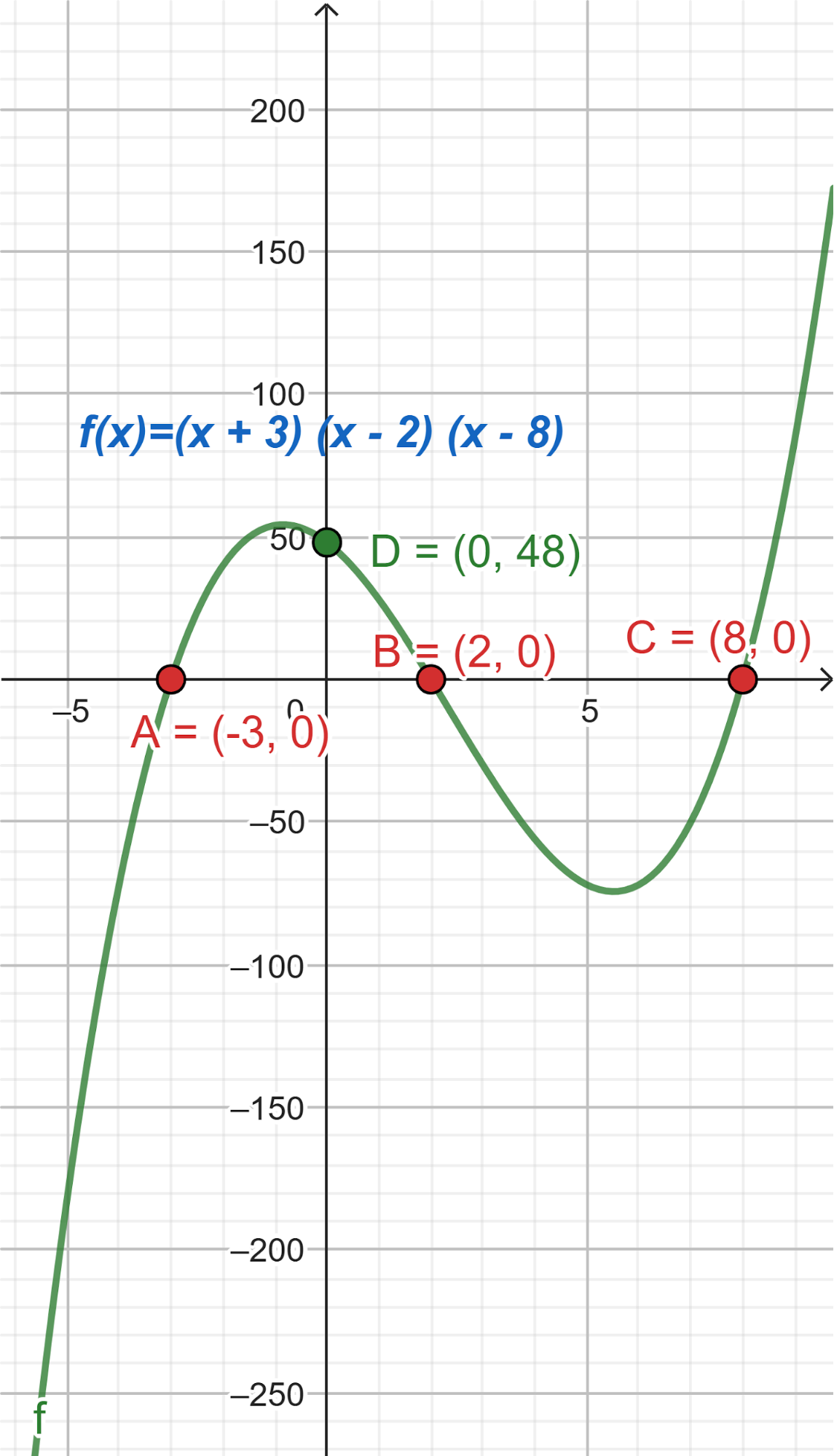
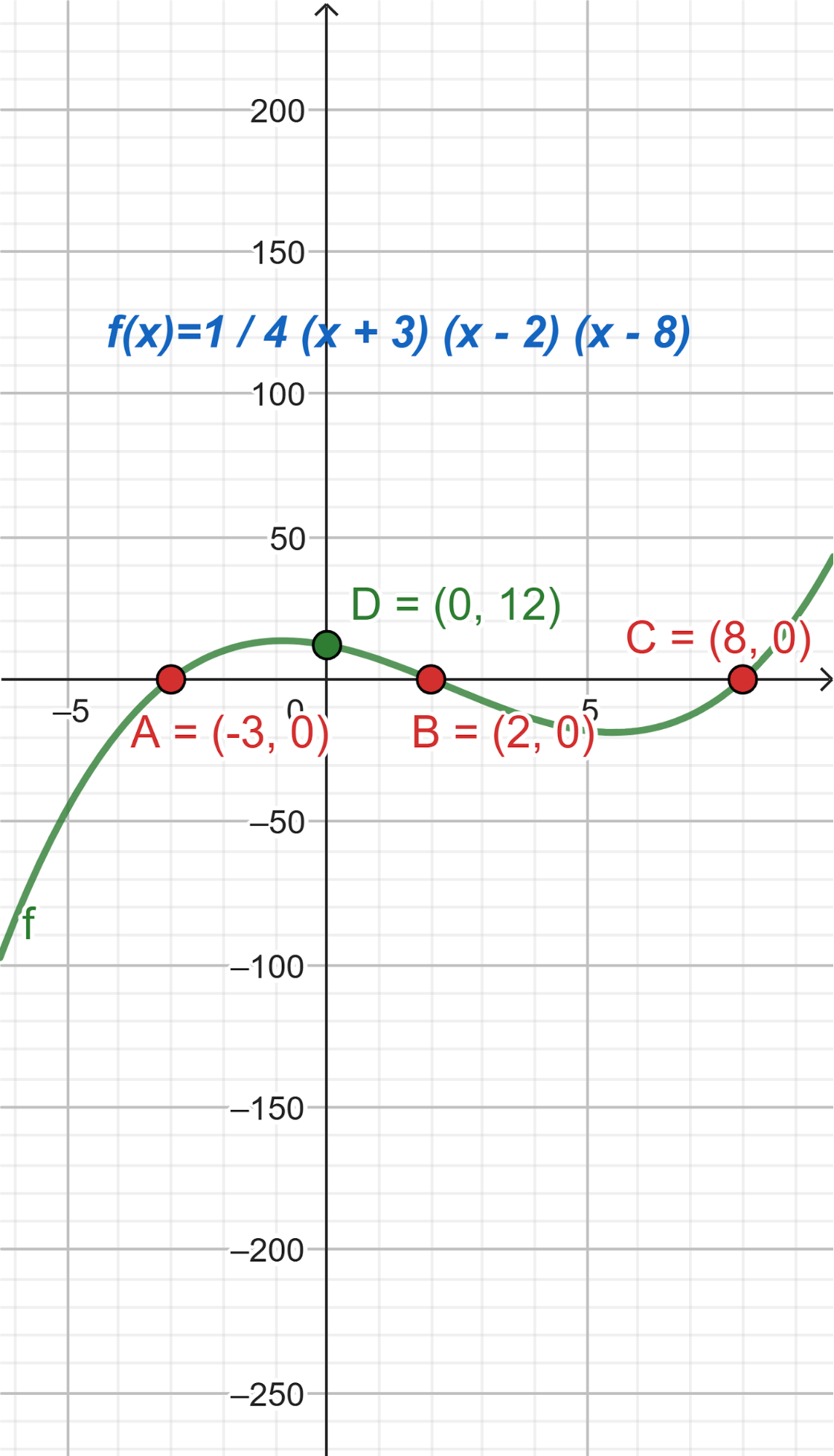
- Las raíces son -3, 2, 8 y el gráfico de corta al eje de las en 12.
Solución:
Evaluamos en :
No cumple siendo el coeficiente principal .
Entonces ¿Cuál debería ser el coeficiente principal para que el corte de ordenadas sea 12?
Por lo tanto:
Cumpliendo que sus raíces sean -3, 2, 8 y el corte de ordenada 12.
La función tras aplicar Propiedad distributiva queda:
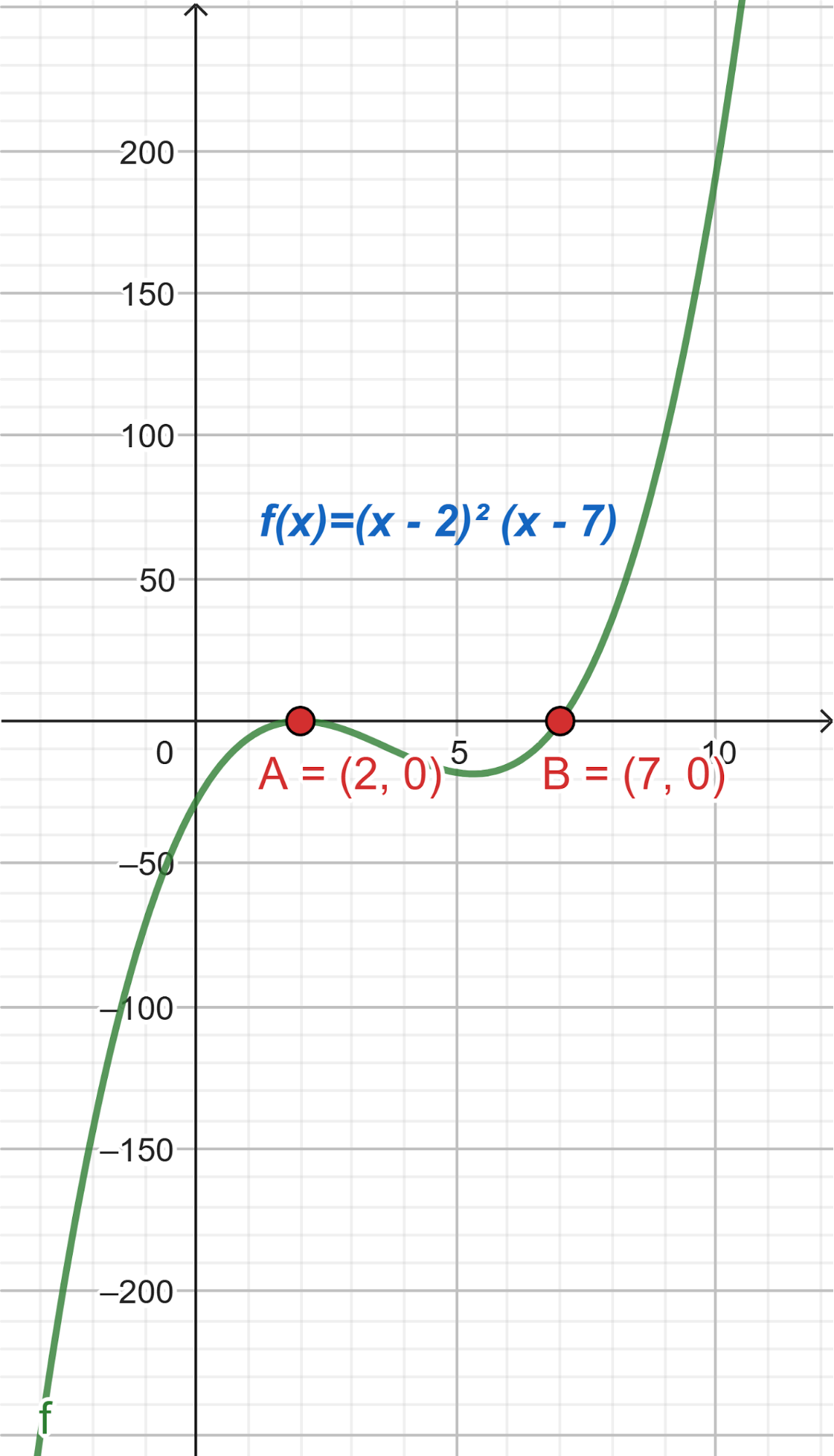
- Las raíces son solamente 2 y 7.
Solución:
- Las raíces sean solamente 0, -1 y .
Solución:
Con
Evaluamos :
No cumple siendo el coeficiente principal .
Entonces ¿Cuál debería ser el coeficiente principal para que ?
Despejamos
Por lo tanto:
Evaluamos:
Cumpliendo que sus raíces sean 0, -1 y
También puede ser:
Con
Evaluamos en :
No cumple siendo el coeficiente principal .
Entonces ¿Cuál debería ser el coeficiente principal para que ?
Despejamos
Por lo tanto:
Evaluamos:
Cumpliendo que sus raíces sean 0, -1 y
La función que encontraron en cada caso, ¿Es la única que cumple esas condiciones? Si creen que sí, justifiquen y si creen que no, hallen al menos tres fórmulas diferentes.
Solución:
Son las únicas que respetarán las pautas, salvo que se puedan poner más múltiplos en .
Problema 12 Escriban, si existe, una fórmula de alguna función cúbica que verifique las condiciones que se piden en cada caso:
- Que tenga un solo cero y esté en .
Solución:
Con
- Que tenga un cero doble en .
Solución:
Con
- Que tenga ceros en , , y en .
Solución:
Va a dar una función de grado 4, no una función cúbica!. Desarrollo:
Comprobando que es una Función de grado 4.
- Que no tenga ceros.
Solución:
Una función cúbica tendrá al menos una raíz real.
- Que tenga un solo cero y que sea cero doble.
Solución:
Basta con agregar un corte de ordenada.
Desarrollada:
Problema 13 La función es el producto de dos funciones: .
- ¿Puede ser que ? Si les parece que sí encuentren . Si les parece que no, justifiquen.
Solución:
Nos aseguramos que la raíz de sea cero de
Evaluamos la raíz de en :
Es cero de la función.
Resolución con Calculadora:
Calculamos las raíces de la función para armar la función en su forma Factorizada, obteniendo:
Por lo tanto podemos armar :
Desarrollamos:
Entonces:
Comprobamos aplicando la Propiedad Distributiva:
Con
Resolución sin Calculadora:
Habiendo verificado que la raíz de es un cero de , planteamos como el producto de una función lineal y una función cuadrática:
Igualamos las funciones y armamos un Sistema de ecuaciones con los coeficientes de igual grado:
Sistema de ecuaciones:
Despejamos c:
Despejamos a
Despejamos b de alguna de las ecuaciones restantes:
Comprobamos en la ecuación restante la igualdad:
Por lo tanto con , , queda:
Siendo :
Aplicamos Propiedad Distributiva para verificar.
Con .
- ¿Y si fuera ?.
Solución:
Nos aseguramos que la raíz de sea cero de
Evaluamos la raíz de en :
No es cero, por lo tanto no pertenece a .
- ¿Es posible escribir como producto de tres lineales?.
Solución:
Si, de hecho es una función cuadrática producto de otras dos funciones lineales:
Quedando :
Aplicamos Propiedad Distributiva para verificar.
Con .
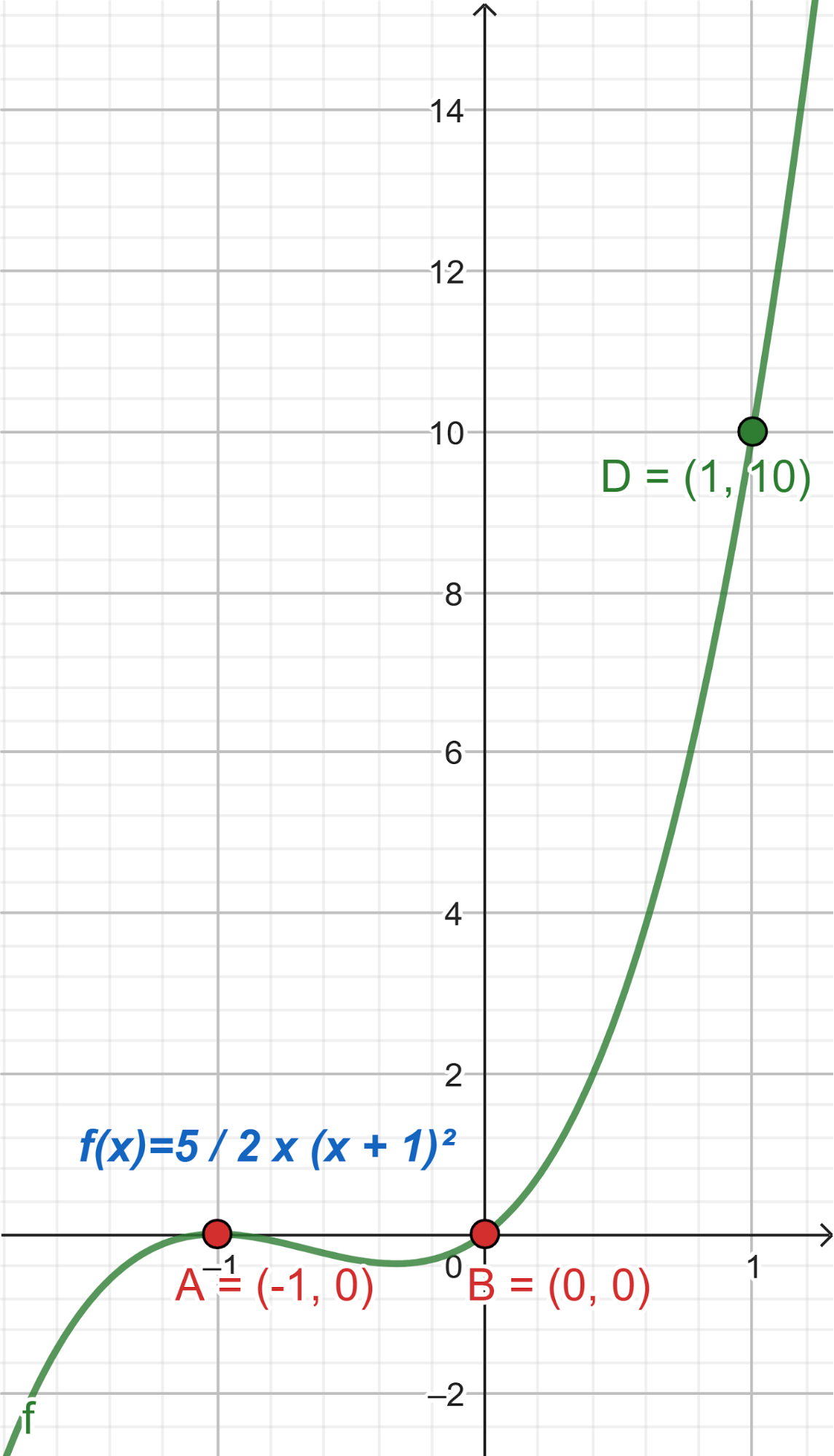
Problema 14 Escriban una fórmula qué pueda corresponder a cada una de las funciones representadas. En cada caso, indiquen qué conocimientos han tenido en cuenta para armar la fórmula:
TP Unidad 3
Problema 1. A partir de láminas metálicas cuadradas de de lado, se van a construir cajas sin tapa de base cuadrada. Para ello se recortan pequeños cuadrados iguales en cada una de las esquinas, lo que permitirá, posteriormente, el plegado de la lámina metálica para armar la caja. Como el material irá soldado, no se necesita dejar pestañas para el armado.
- Si una caja es tal que su base es de ¿Cuál es su volumen?.
Solución:
Con y
Evaluamos :
Su volumen es de .
- ¿Habrá otra caja con el mismo volumen que la caja del ítem anterior?. Si la respuesta es no, justifiquen. Si la respuesta es sí, determinen analíticamente las dimensiones de todas las cajas posibles.
Solución:
Si, existen otras 2 cajas con el mismo volumen ya que la función es de grado 3 y el coeficiente principal Positivo.
Conociendo que es solución, con lo cuál será un cero de una función de grado de la cuál debemos hallar sus otros dos ceros. Para ello igualamos la función en su forma Factorizada o Desarrollada a 7056:
Forma Desarrollada:
Igualamos a cero y mediante Ruffini, tomando 4 como factor, hallamos una función cuadrática y luego sus raíces.
- Coeficientes: 4, -200, 2500, -7056.
- Factor 4.
4 | -200 | 2500 | -7056 | |
4 | 16 | -736 | 7056 | |
4 | -184 | 1764 | 0 |
Quedando la función:
Calculamos sus ceros mediante la resolvente:
Con:
- a = 4.
- b = -184.
- c = 1764.
|
|
32,38 | 13,62 |
Entonces las raíces de la función son:
Y si evaluamos estos ceros en confirmamos que obtenemos el mismo volumen:
Para :
Para :
Buscando exactitud utilizamos:
Forma Factorizada:
Desarrollamos el polinomio hasta llegar a la misma función a partir de la cual buscamos sus raíces mediante Ruffini obteniendo solucionando con la resolvente y verificando.
- Con ayuda de algún software, determinen si existe una caja con volumen máximo. En caso de que exista, determinen las dimensiones de tal caja.
Solución:
Al graficar en GeoGebra y utilizar la herramienta Extremos Relativos podemos observar que el máximo volumen se dá cuando con un volumen de
Evaluamos :
La dimensión de la caja será de obviamente a fines prácticos se recortará una caja de o .
