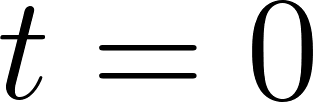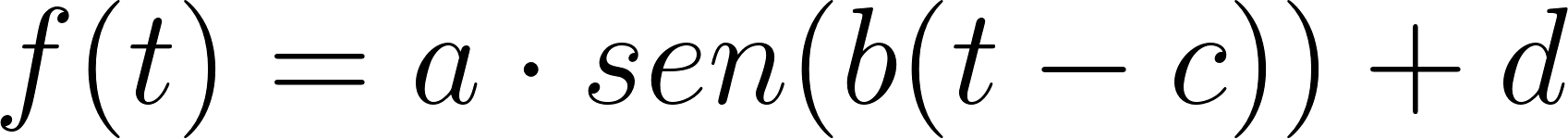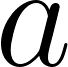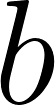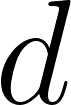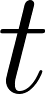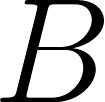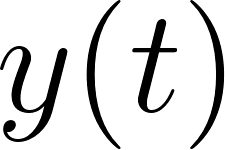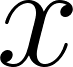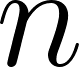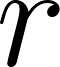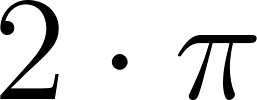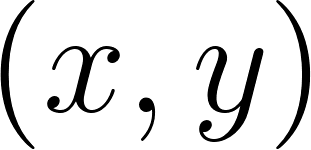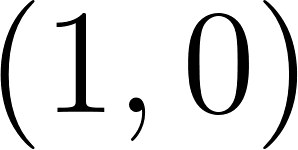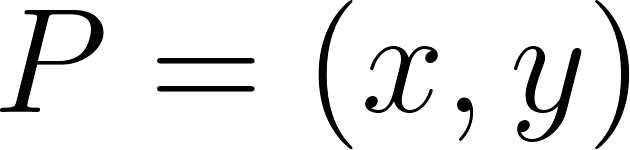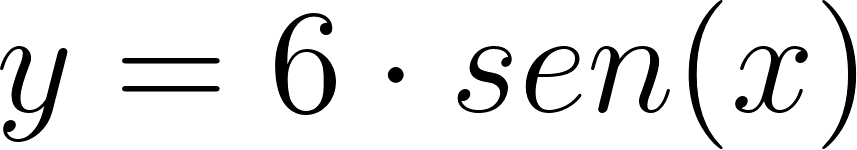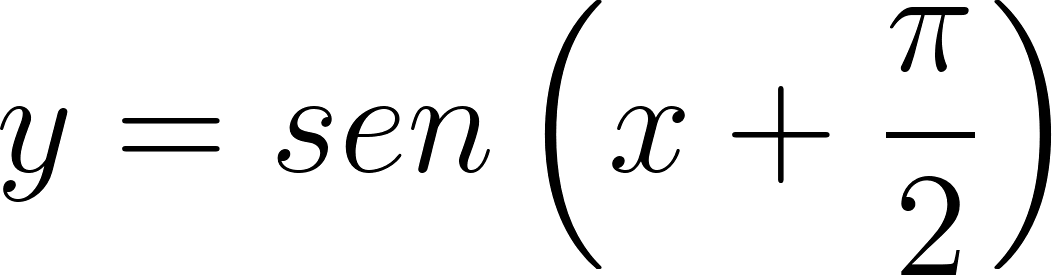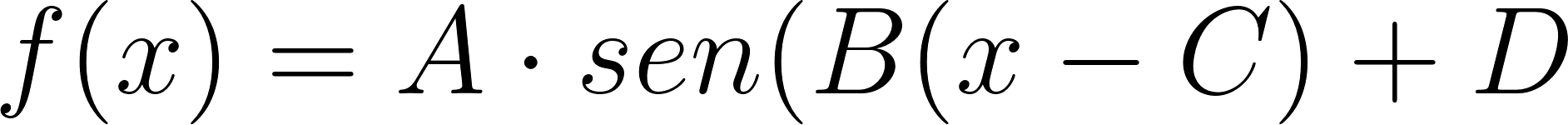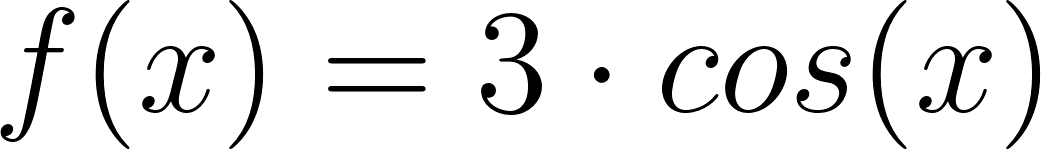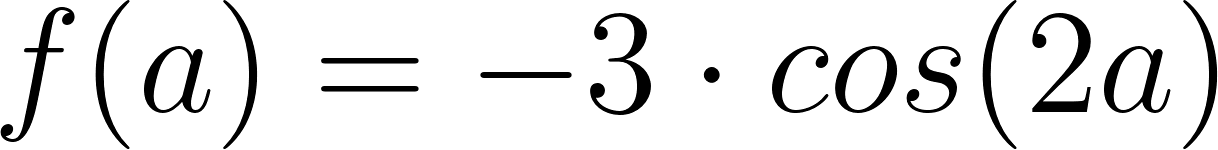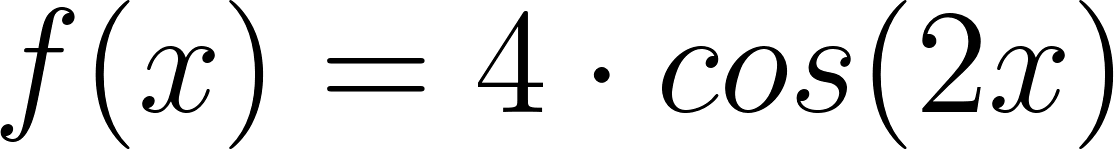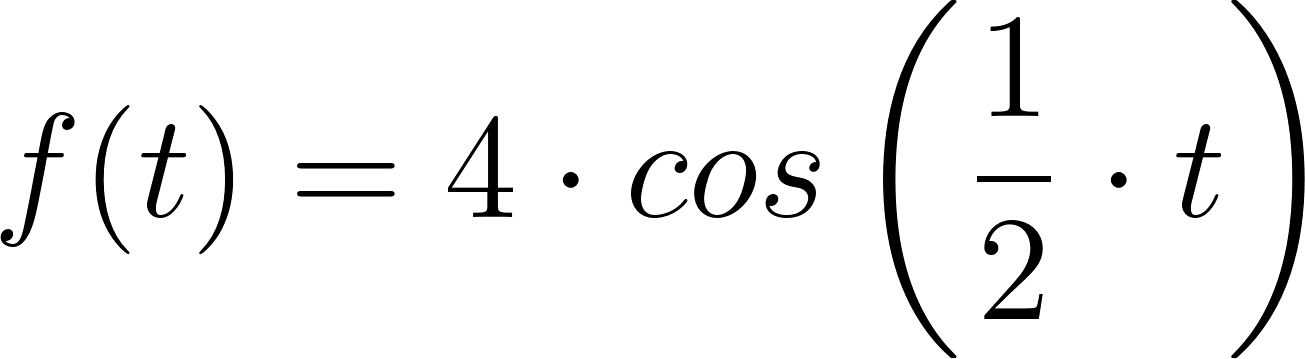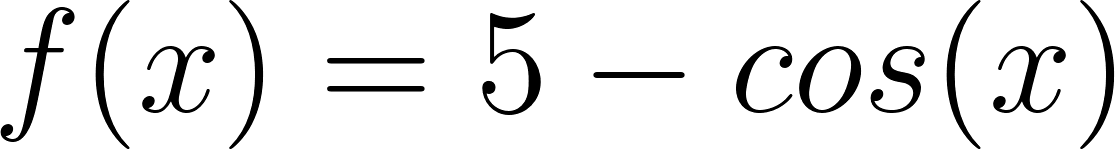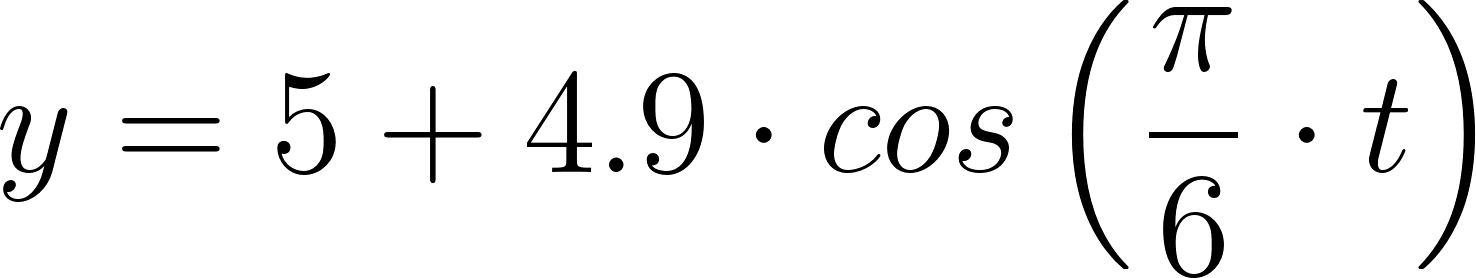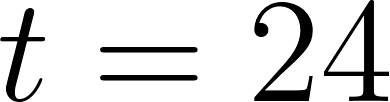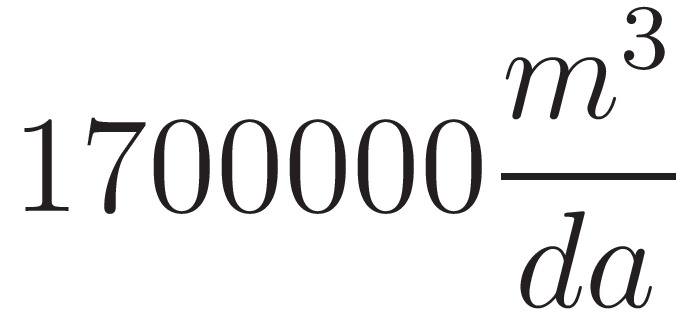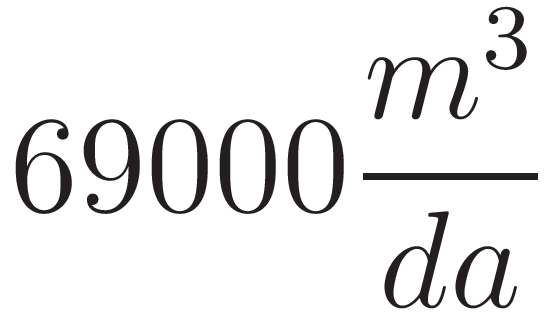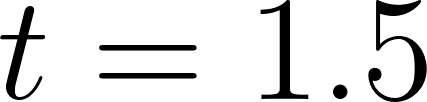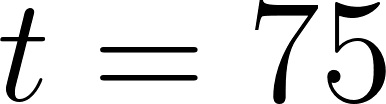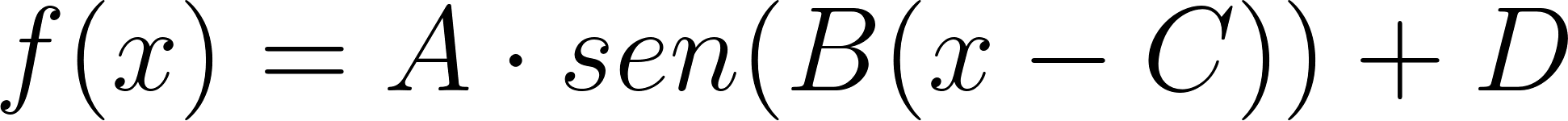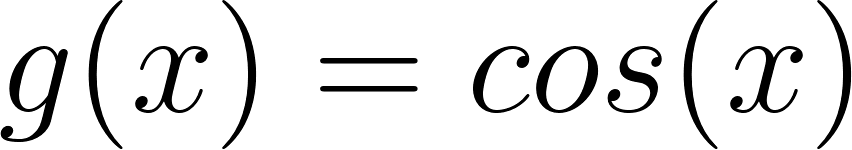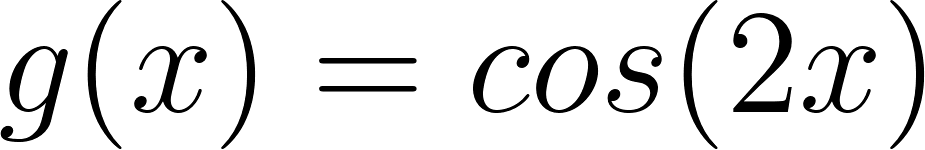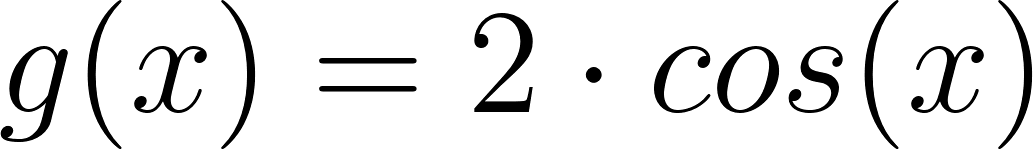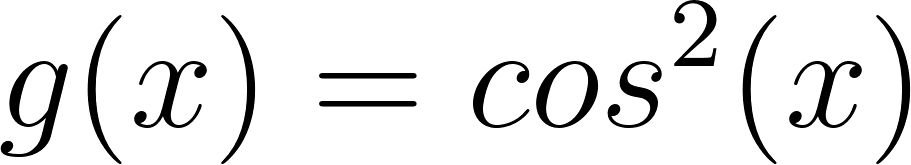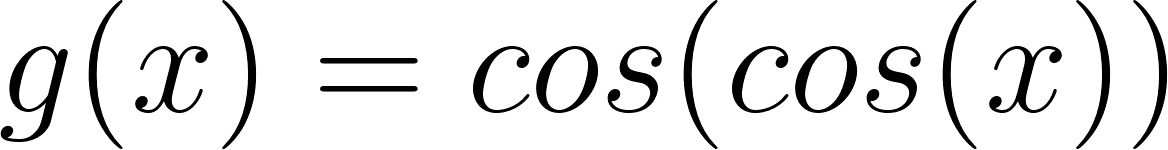Funciones Trigonométricas
Teoría:
- Genially Modelos Oscilatorios
- Empezamos con un problema: Problema Noria
- Les dejamos un archivo de GeoGebra que los ayudará a encontrar la solución del problema del Ojo de Londres. Applet por Pingaro. [.ggb]
- Que no cunda el pánico una solución. Les dejamos un VIDEO donde se resuelve el problema.
- Queres saber mas sobre las funciones trigonométricas: Parámetros de la función seno | CURSO de TRIGONOMETRÍA Clase #15
- Más videos para seguir conociendo estas funciones:
- Funciones trigonométricas-Parte I
- Funciones trigonométricas-Parte II
- Funciones trigonométricas-Parte III
- Páginas 273 a 284 de este libro: Iniciación Matemáticas para ingeniería.
- Para seguir pensando: Problema de Sol.
- Resolución Ecuaciones Trigonométricas.
Unidad 6
“Modelos oscilatorios”
Guía:
Objetivos de esta unidad:
|
Problema 1.
El Ojo de Londres se puede modelizar por medio de una circunferencia de 120 metros de diámetro, cuyo centro se encuentra a 75 metros sobre el nivel del suelo.
Supongamos –vista desde el Támesis– que la rueda gira en sentido antihorario a razón de 2 revoluciones por hora. Queremos obtener un modelo que permita obtener la altura de cierta canastilla (podemos considerarla como un punto a los fines de la modelización) para cada instante de tiempo, sabiendo que al tiempo le corresponde la posición más baja que se puede encontrar la canastilla en cuestión.
Construyan el modelo (la función) e indiquen todos los razonamientos involucrados.
Problema 2.
En el Applet Ojo de Londres está graficada la función para ciertos valores de , , y . Cada uno de los parámetros puede modificarse moviendo los deslizadores correspondientes. Hallen, con ayuda del Applet, la función que indica la altura de la silla del problema anterior. Relacionen los valores de los parámetros con los datos del Problema 1.
Problema 3 ().
Para trabajar con este problema necesitan abrir el Applet Marea en la que verán, como si tuvieran un catalejo, un faro a orillas del mar. Exploren el archivo y escriban un texto de no menos de 150 palabras que describa lo que se puede observar.
Problema 4.
Utilicen los recursos de GeoGebra que crean convenientes para investigar cómo varía la altura de la marea en función del tiempo, en el problema anterior. En una segunda parte de la actividad les preguntaremos cuál será la altura de la marea en un determinado momento y tendrán que poder responder, sin tener acceso al Applet.
Problema 5 ().
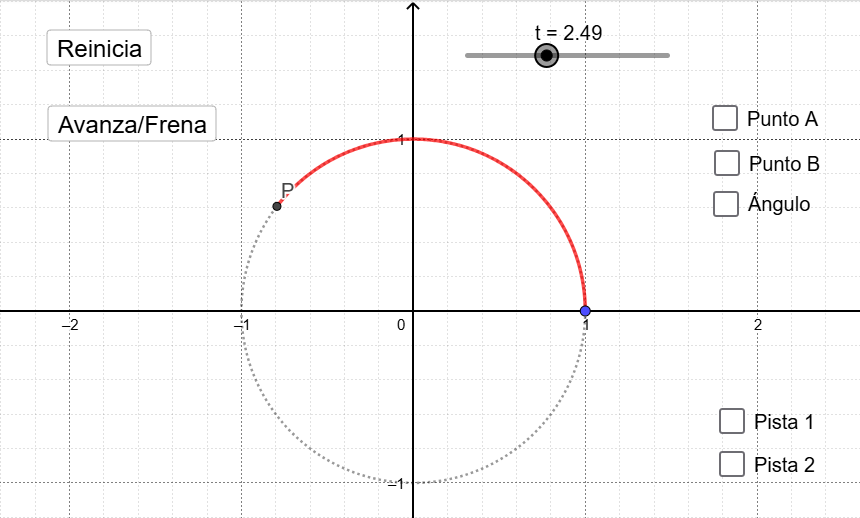
Para estudiar este problema usaremos el Applet de GeoGebra Movimiento oscilatorio [Explica en palabras, haciendo tablas de valores o gráficos, qué relaciones hay entre el parámetro , la posición del punto y las posiciones de los puntos y . Estudia , y por separado. Si no se te ocurre, habilita la Pista 1 y luego la Pista 2.].
Para entender lo que sigue conviene que tengan el Applet abierto y vayan leyendo mientras lo ven funcionar.
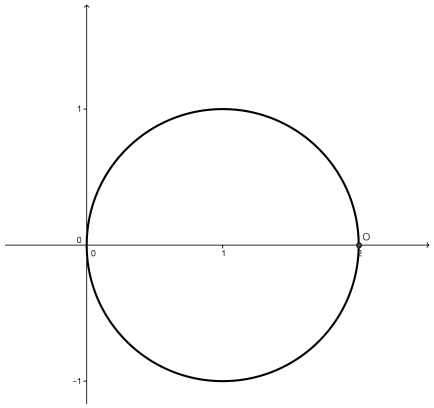
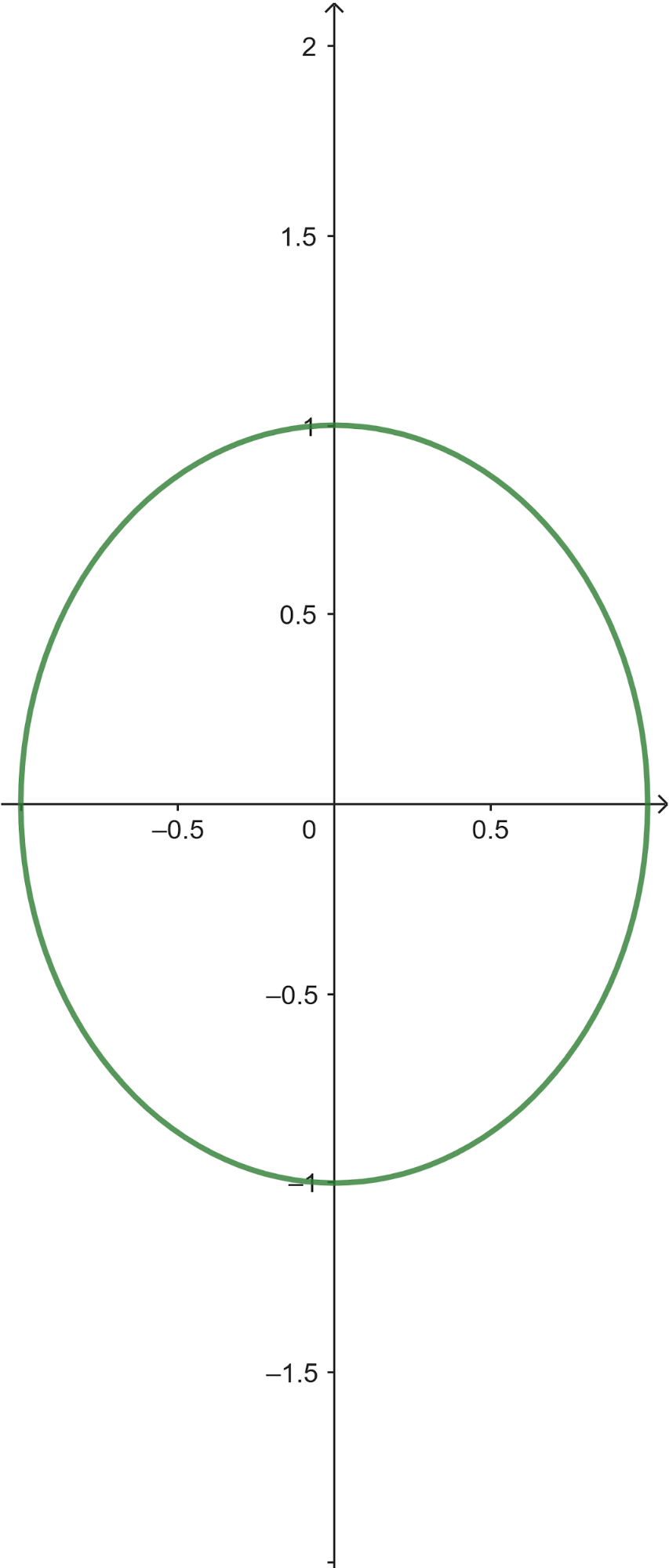
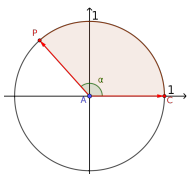
Verán un escenario como el de la siguiente figura:
El punto gira alrededor de la circunferencia de radio 1 y va dibujando un arco rojo de longitud . Vamos a definir dos funciones y ustedes tendrán que jugar con el Applet para reunir la información que les permita dibujar en una hoja los gráficos de las dos funciones.
Se definen dos funciones e como las coordenadas e del punto en función de la distancia recorrida en su tránsito por la circunferencia, en el sentido contrario a las agujas del reloj. El applet tiene opciones que pueden activar o desactivar, para apreciar distintos detalles. Es tarea de ustedes interpretar para qué les pueden servir esos detalles
Entonces la consigna concreta es: Dibujen en un sistema de coordenadas los gráficos de e .
Problema 6.
Análisis de las funciones e . Imaginando la situación a partir de la figura del Problema 5, piensen las siguientes preguntas:
- ¿Cuál es el mayor valor que puede alcanzar ?, ¿Y el menor? ¿Para qué valores de se producen?.
- ¿En qué intervalos crece la función ?, ¿En qué intervalos decrece?.
- Antes de seguir, vean si hay consistencia –es decir, no hay contradicciones– entre las respuestas de los dos puntos anteriores.
- Encuentren 10 valores de tales que .
- Repitan todo el mismo análisis para la función , copiando el análisis de la función y adaptando todo lo que sea necesario.
- ¿Qué relación existe entre alguna de las funciones definidas y el Problema 1?.
Problema 7.
Estudien las funciones e correspondientes a cada una de estas circunferencias, siempre comenzando el recorrido en el punto y girando en sentido contrario al de las agujas del reloj.
Problema 8.
Lean el siguiente recuadro:
Llamamos circunferencia trigonométrica a la que tiene su centro en el origen de coordenadas y cuyo radio mide 1: |
Consideramos un hecho aceptado que la longitud de una circunferencia es donde es el radio. Por lo tanto, la circunferencia trigonométrica tiene una longitud de . Un punto cualquiera de la circunferencia puede representarse con un vector que nace en el origen y termina en el punto. |
Además, el punto puede identificarse de dos maneras:
|
En el Problema 5 definimos las funciones e como las coordenadas del punto . Ahora les ponemos los nombres que verdaderamente llevan en los libros de cálculo. |
Definición: Sea un ángulo (número real) determinado por una posición de un punto sobre la circunferencia trigonométrica, como se describió más arriba. Se llama coseno de a la coordenada del punto y se llama seno de a su coordenada . Es decir: |
Hacia el final de la materia tendremos recursos para demostrarlo y para definir formalmente a qué se llama longitud de una curva. |
Expliquen cómo las gráficas de cada una de las siguientes funciones difieren de la gráfica de
Problema 9 ().
Determinen cuáles son los cambios que se realizaron en la gráfica de la función para distintos valores de los parámetros , , y . Sugerencia pueden utilizar el Applet del Problema 2.
Problema 10 ().
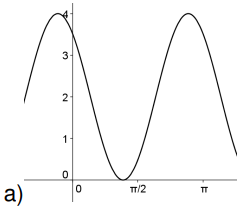
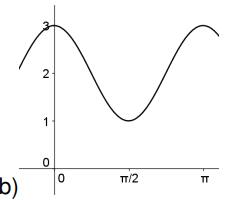
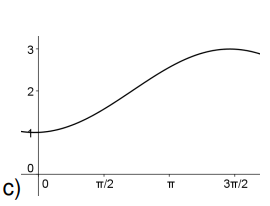
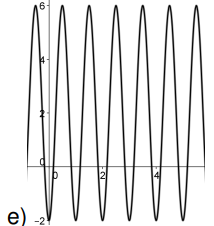
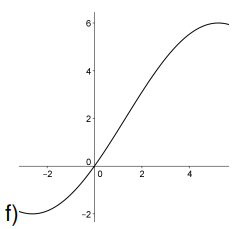
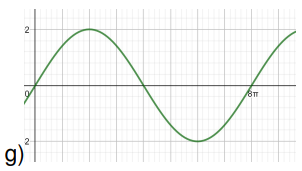
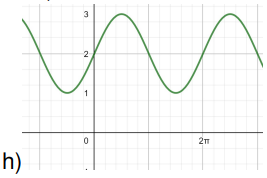
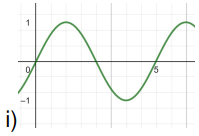
Encuentren posibles fórmulas para funciones que tengan cada una de las siguientes gráficas:
Problema 11.
Dadas las siguientes funciones trigonométricas:
- Anticipen antes de graficarlas, aportando detalles concretos, cuáles pueden ser sus gráficas.
- Indiquen dominio, imagen, período, amplitud, intervalos de crecimiento y de decrecimiento.
Problema 12.
Para las funciones trigonométricas del Problema 11.
- Hallen sus raíces.
- Hallen el conjunto imagen.
- Hallen los valores del dominio en que la imagen vale 2.
Problema 13.
El 10 de febrero de 1990 la marea alta en una ciudad costera de EE.UU fue a medianoche. La altura del agua en el puerto es una función periódica, ya que oscila entre las mareas alta y baja. Si se mide en horas desde la medianoche, la altura (en pies) se aproxima mediante la fórmula:
- Tracen la gráfica de esta función de a .
- ¿Cuál fue el nivel del agua en la marea alta?.
- ¿Cuándo estaba baja la marea y cuál fue el nivel del agua en ese momento?.
- ¿Cuál es el período de esta función y qué representa en términos de mareas?.
- ¿Cuál es la amplitud de esta función y qué representa en términos de mareas?.
Problema 14.
Luego de realizar una investigación acerca de las características que presenta el río Reconquista un grupo de investigadores presentó los siguientes datos sobre el caudal del mismo:
Caudal Máximo | |
Caudal Mínimo |
Además obtuvieron que el caudal máximo se produjo a la medianoche. Asumiendo que la próxima medición que dé como resultado el caudal máximo será al mediodía y que el valor del caudal está representado por una función seno o una función coseno:
- ¿Cuál es el caudal promedio?.
- ¿Cuál es la diferencia entre el caudal máximo y el mínimo? .
- Encuentren una fórmula que represente el caudal del río Reconquista en función del tiempo.
- Representen la situación gráficamente.
- ¿Cuál es el caudal del río a las 3 de la tarde? ¿Y a las 3 de la mañana?.
Problema 15 ().
Los valores de una función se indican en la siguiente tabla. Expliquen por qué esta función parece ser periódica. ¿Aproximadamente a qué son iguales el período y la amplitud de la función? Suponiendo que la función sea periódica, calculen su valor en , en y en .
20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 | |
1.8 | 1.4 | 1.7 | 2.3 | 2.0 | 1.8 | 1.4 | 1.7 | 2.3 |
Problema 16 ().
En cada caso determinen las constantes , , y de manera que la función sea equivalente a la función o den argumentos indicando porque no es posible.
- .
- .
- .
- .
- .
- .
Aprovechen las equivalencias que logren para desarrollar identidades trigonométricas.