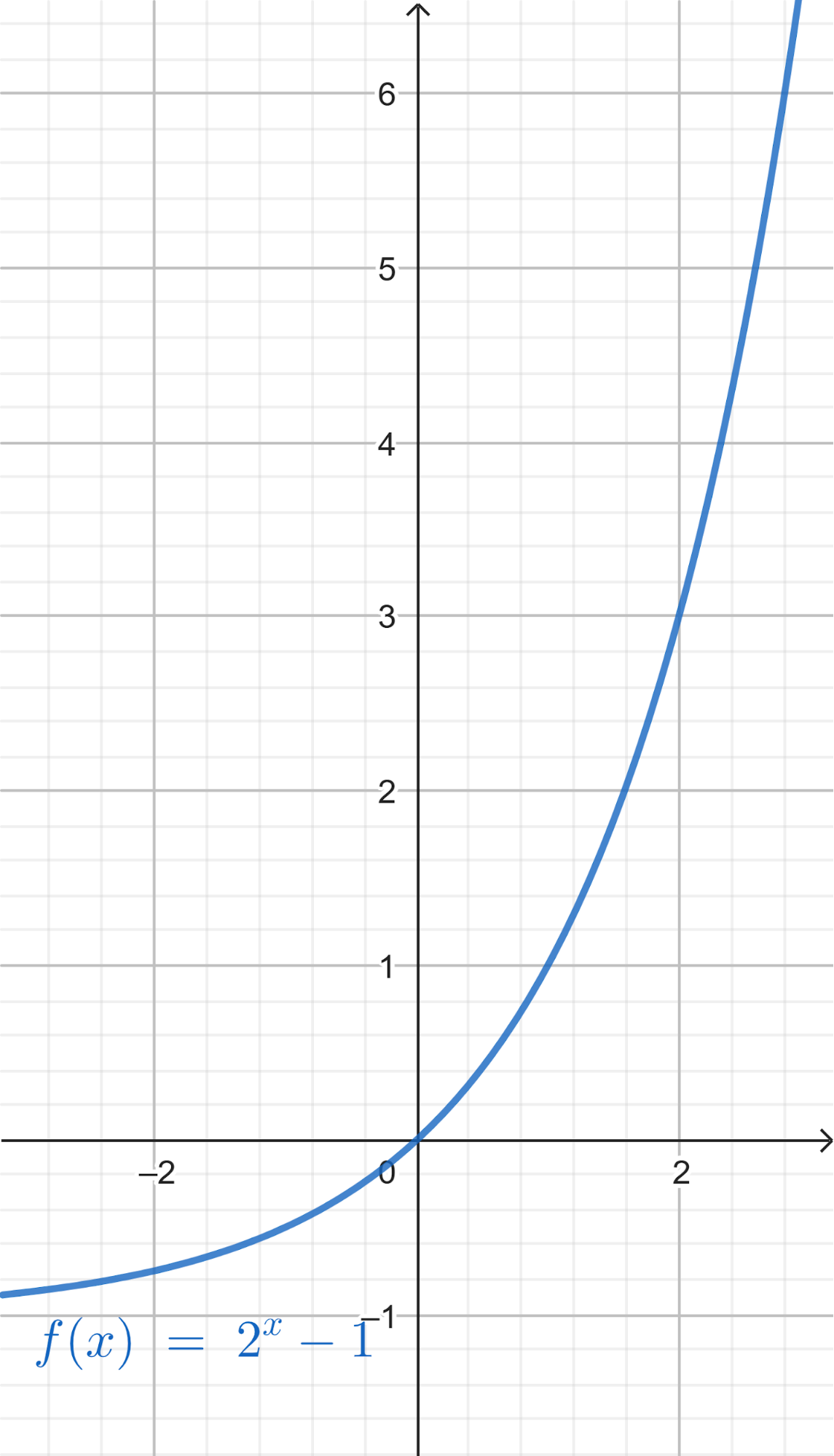
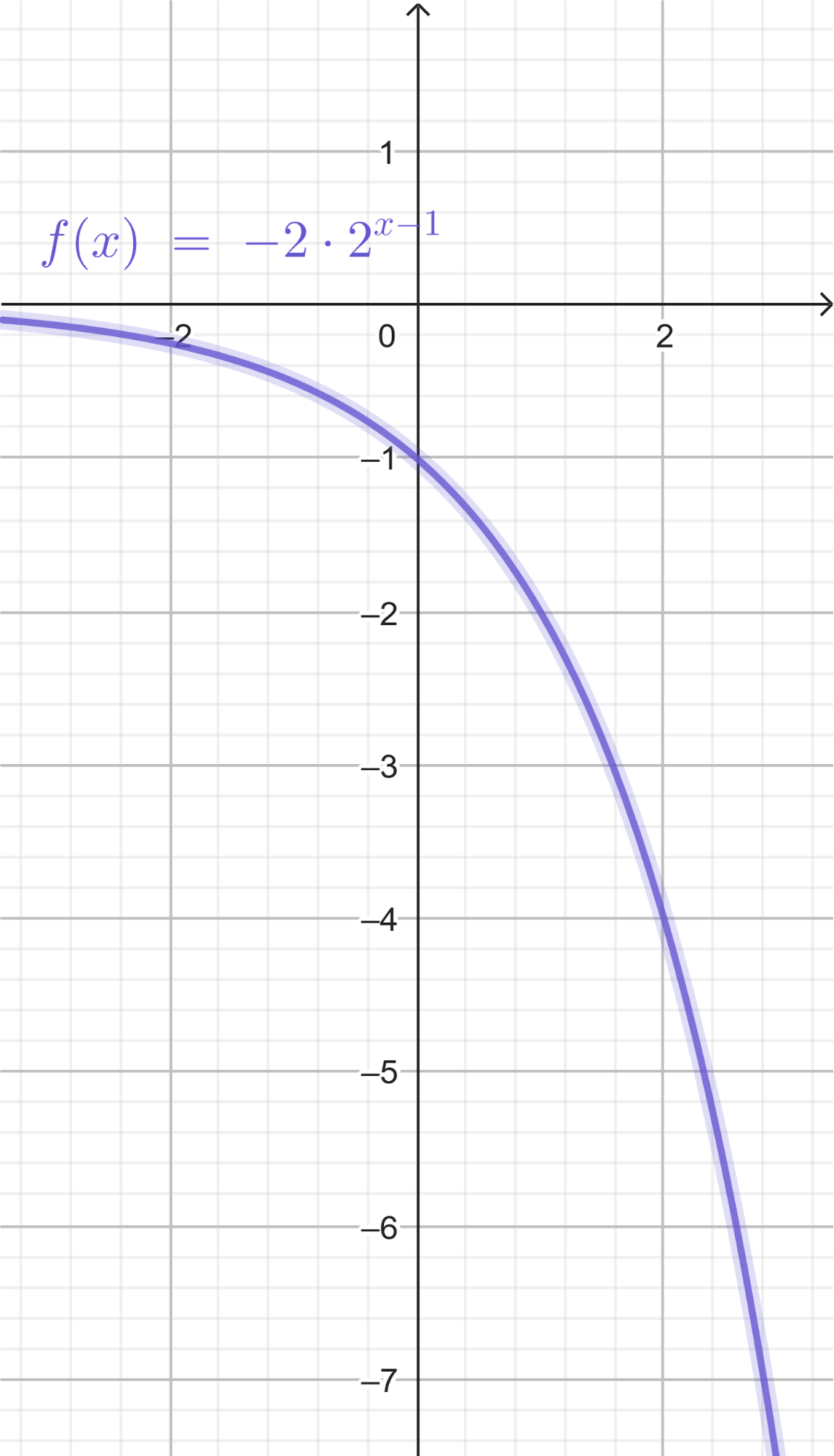
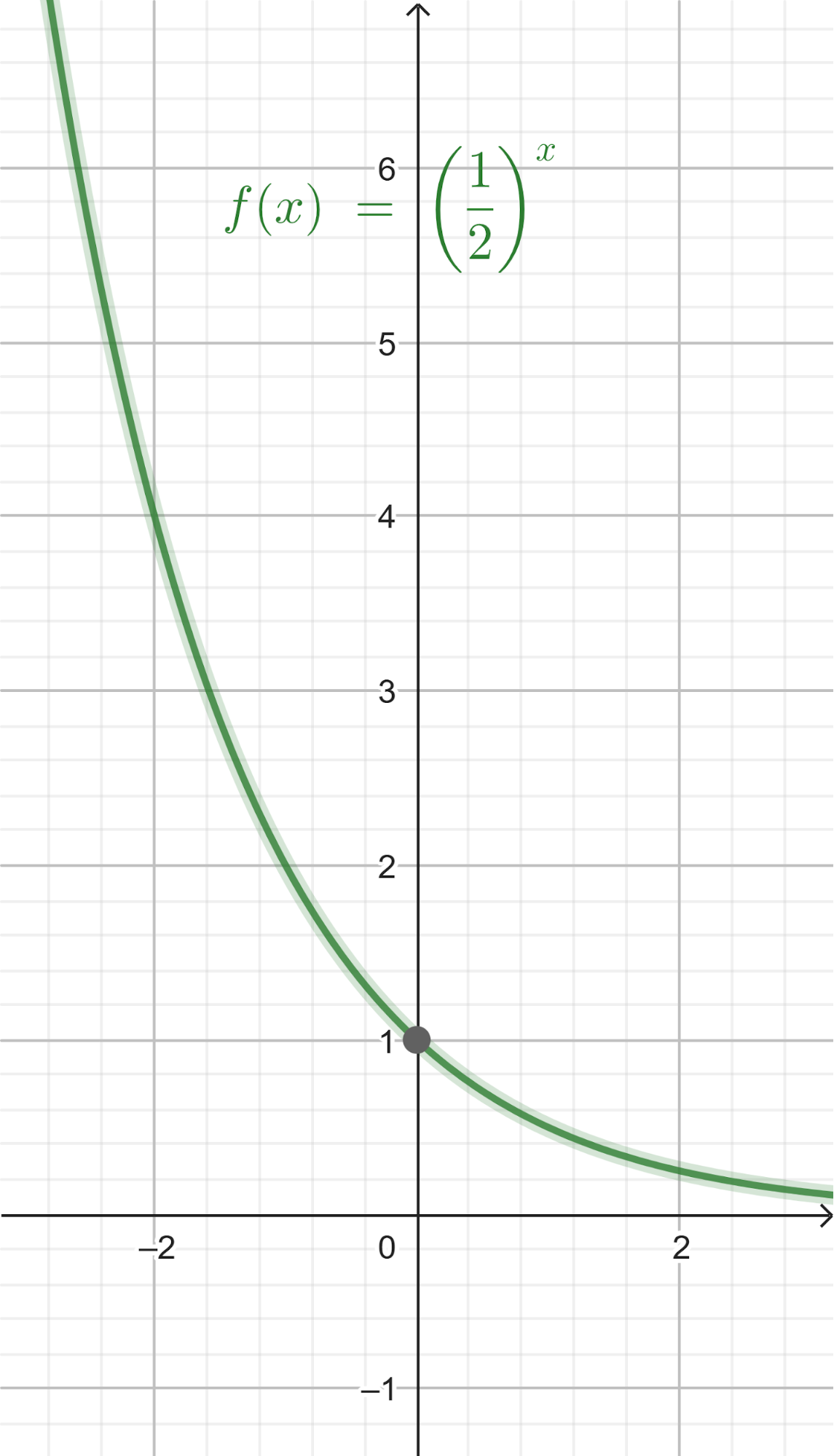
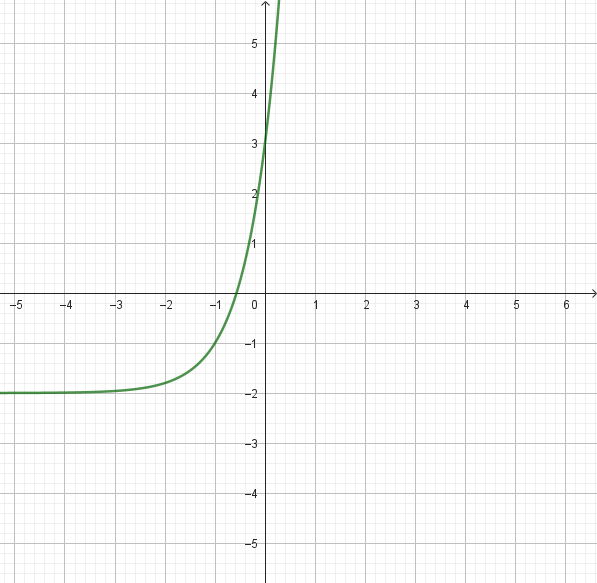
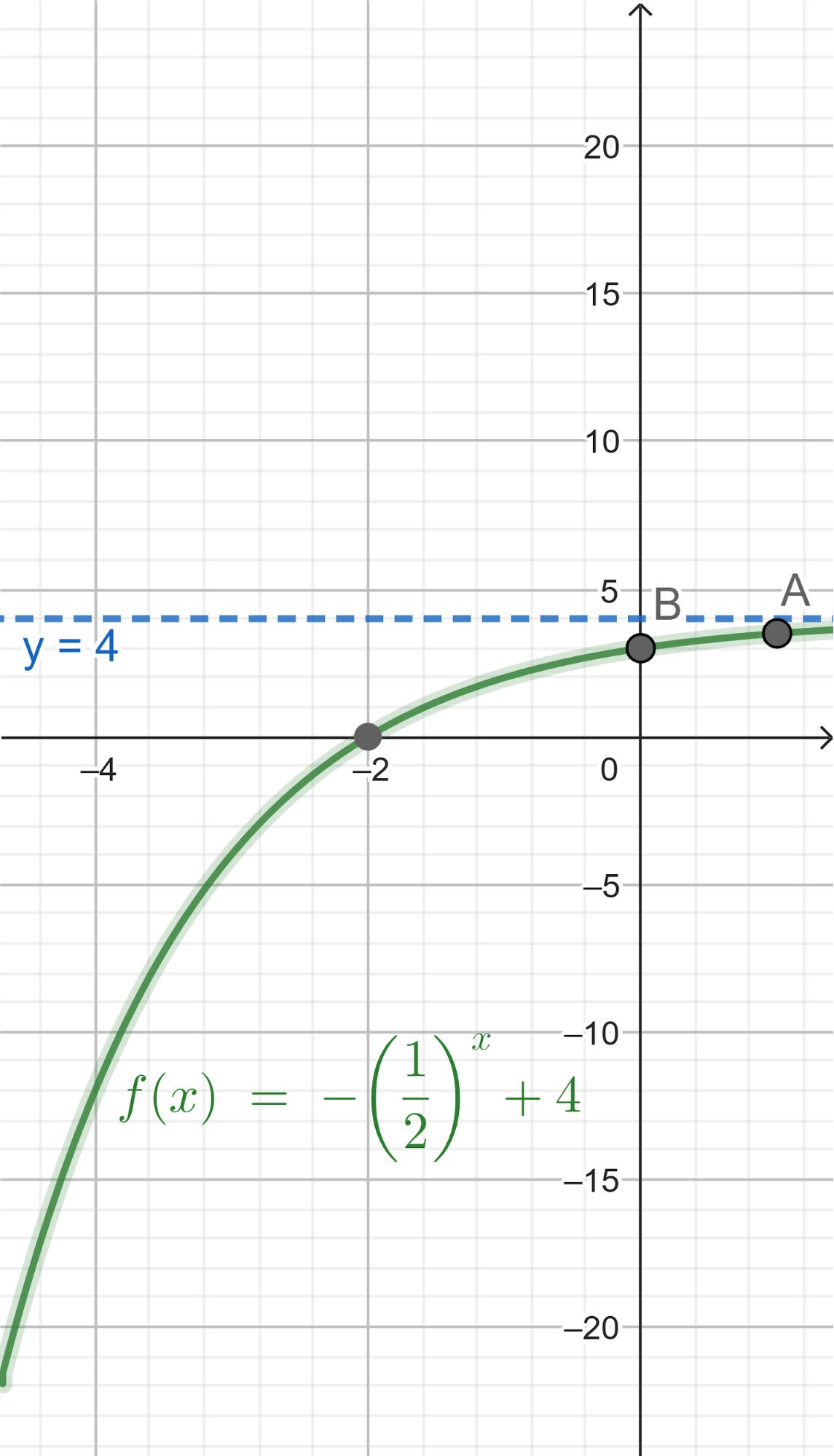
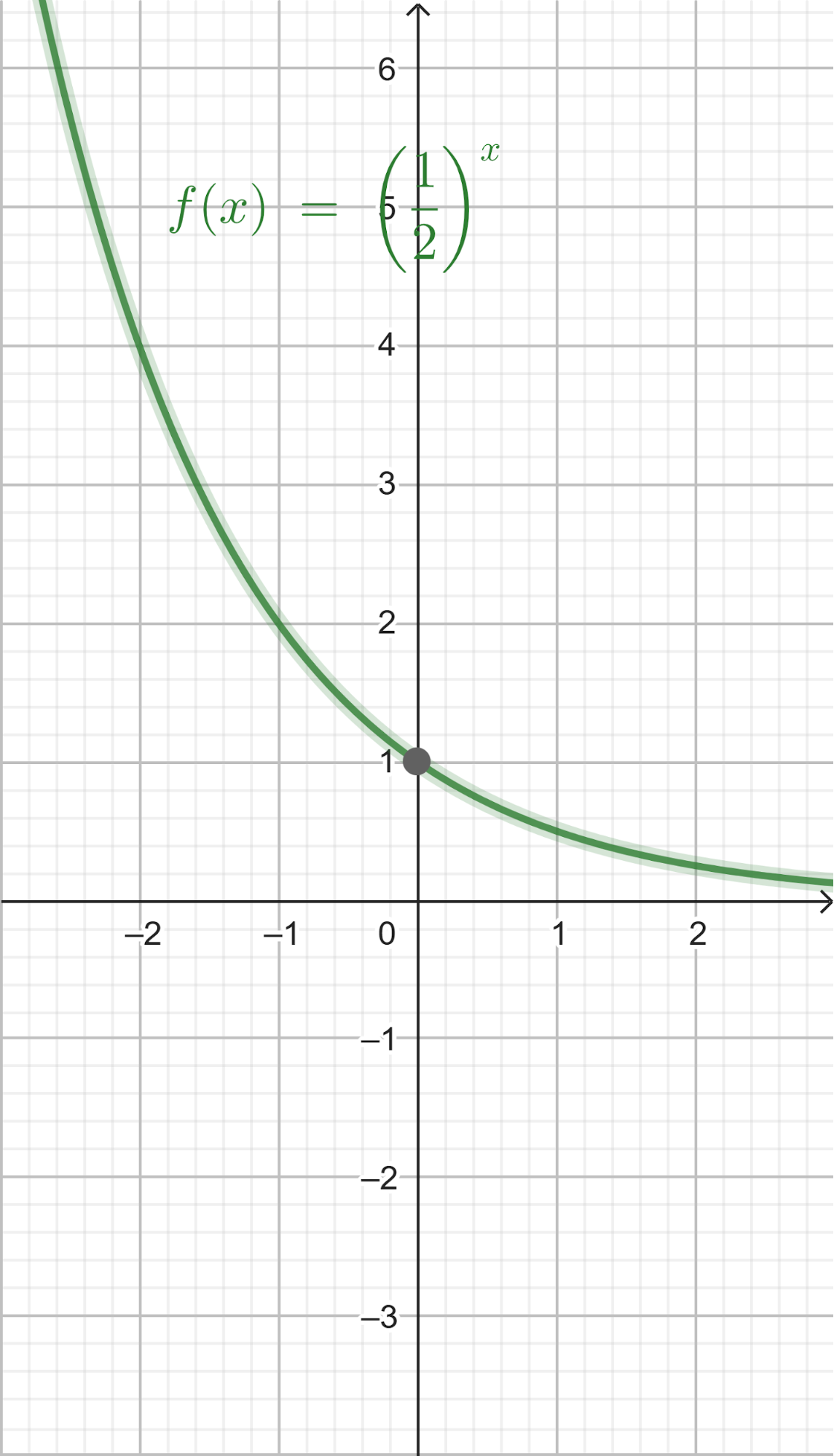
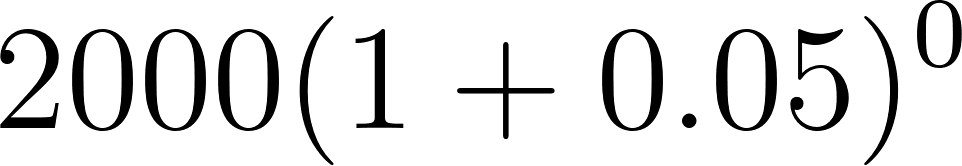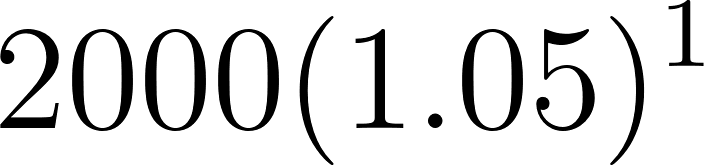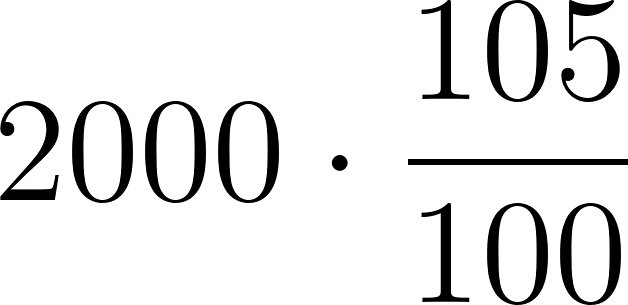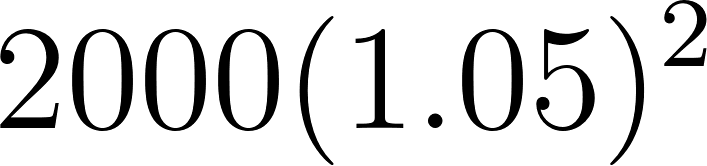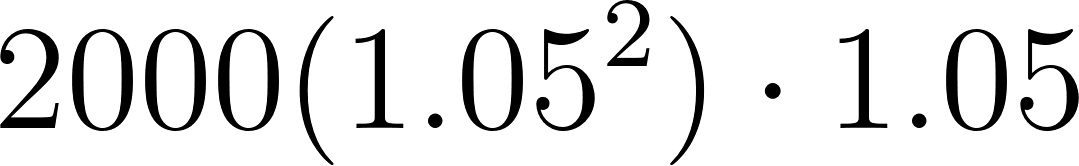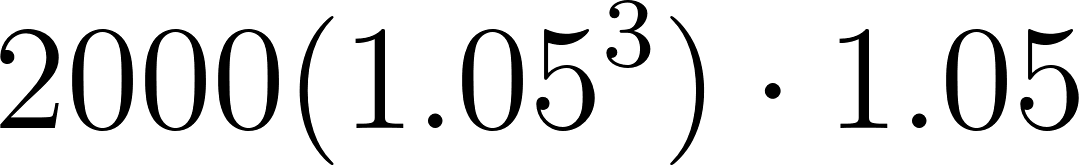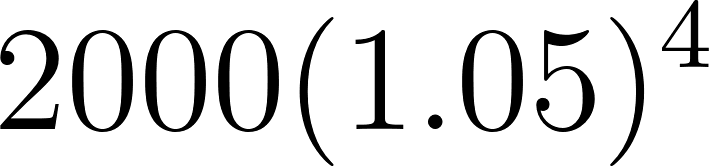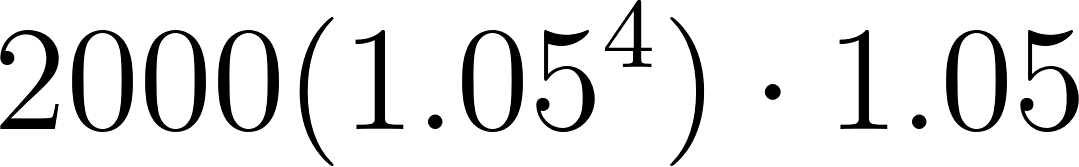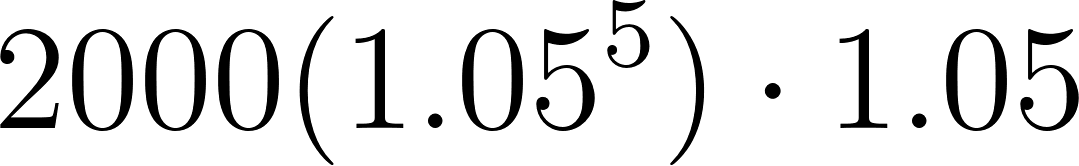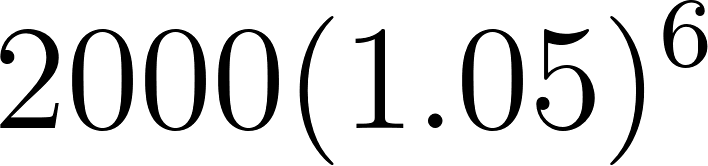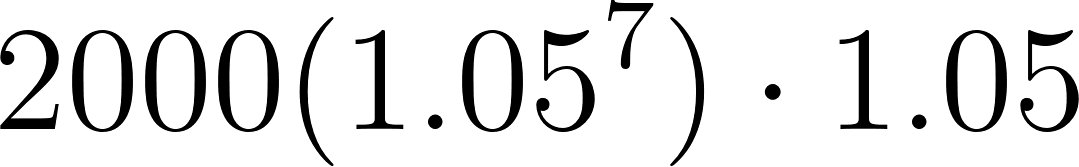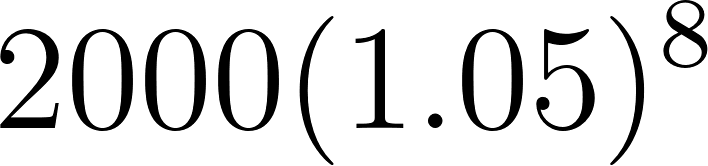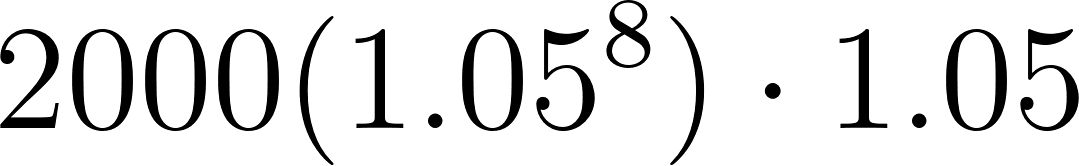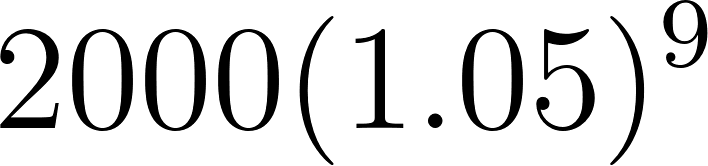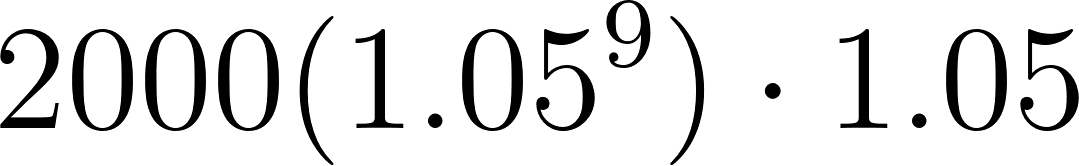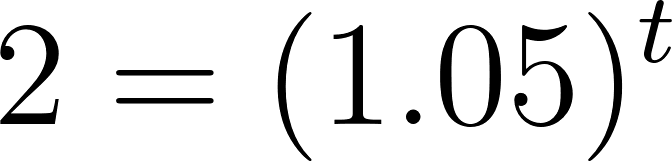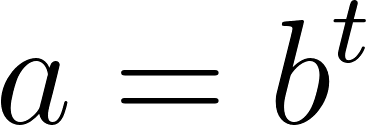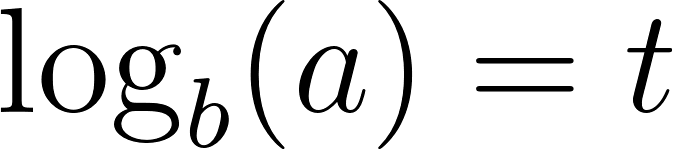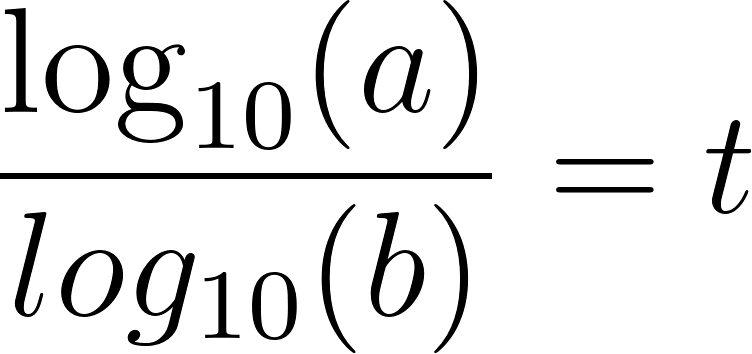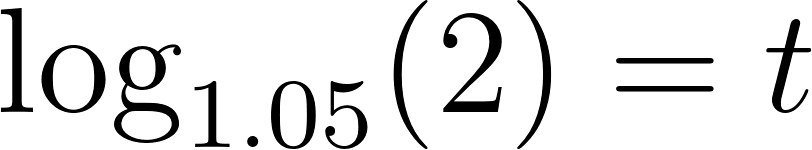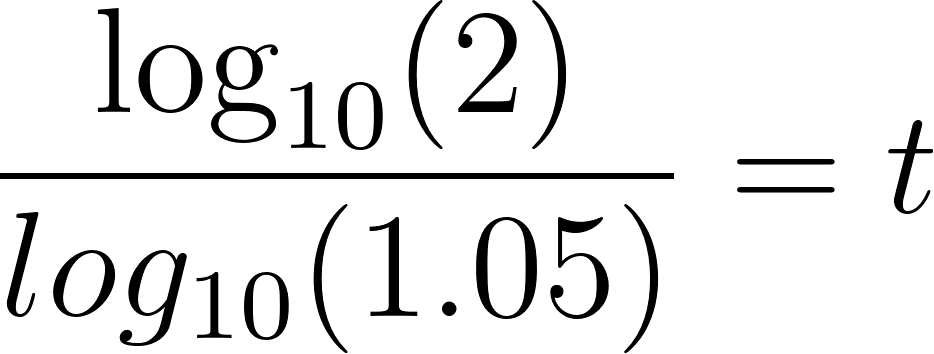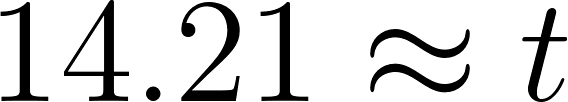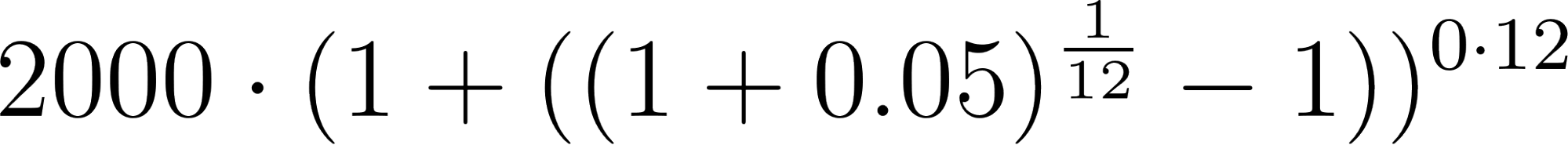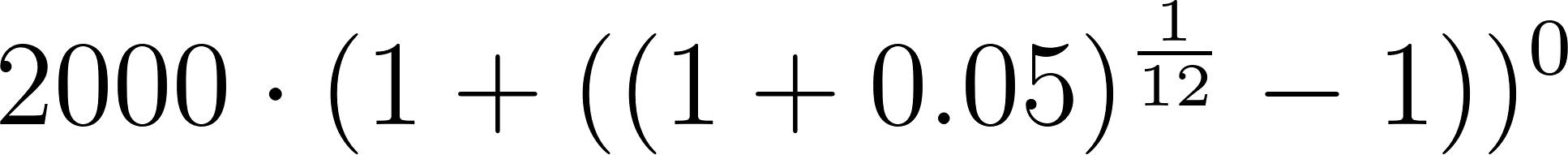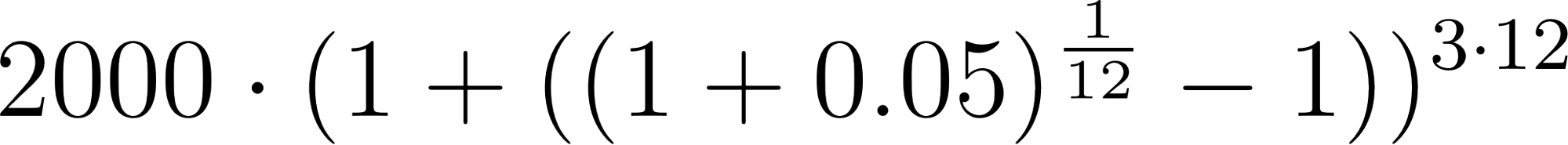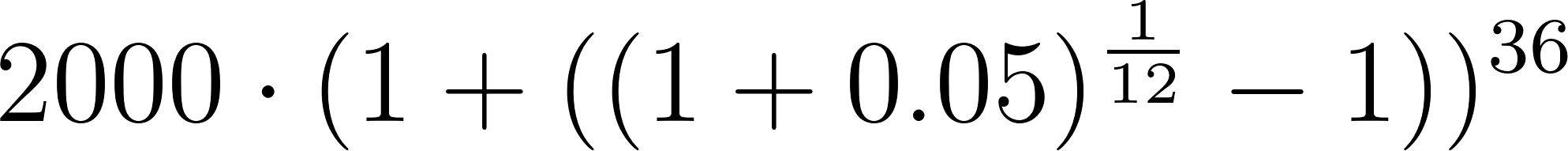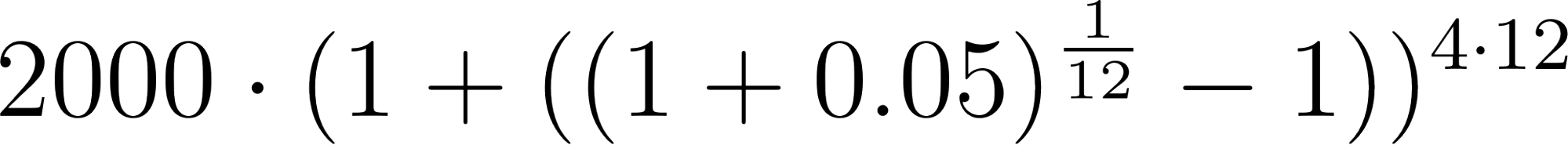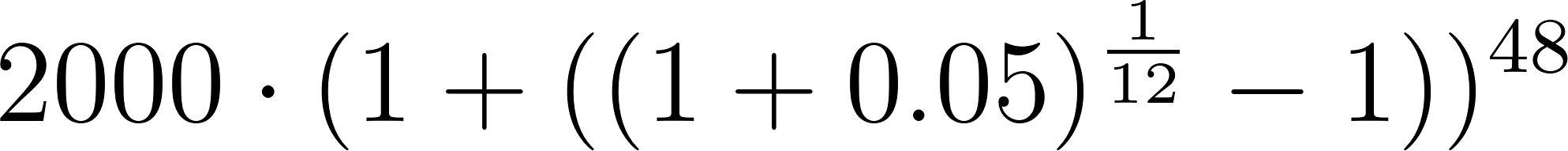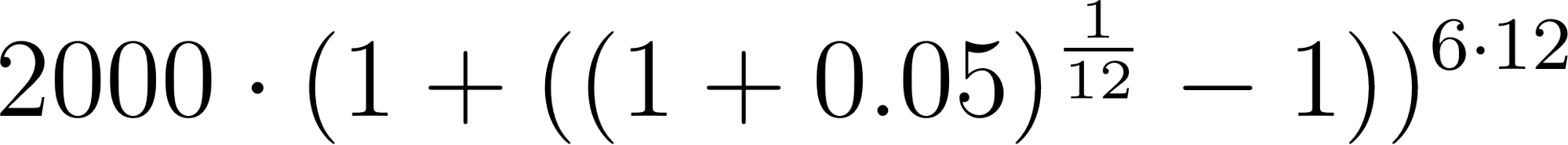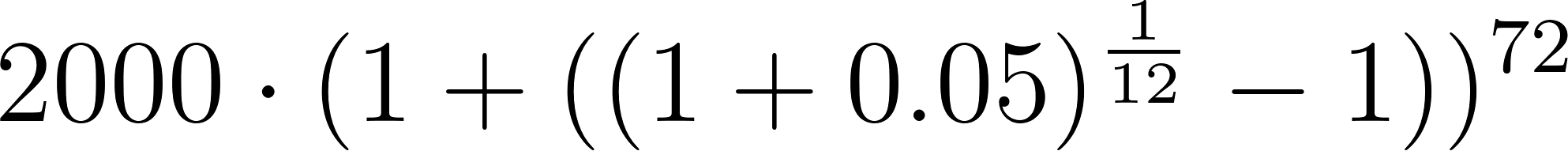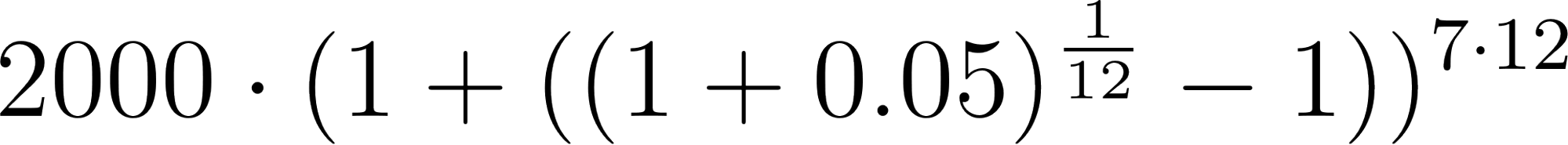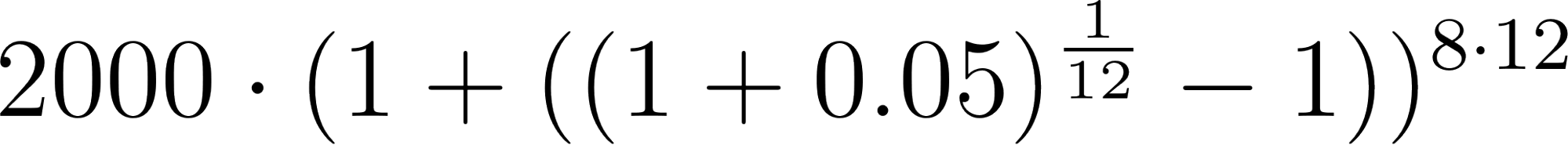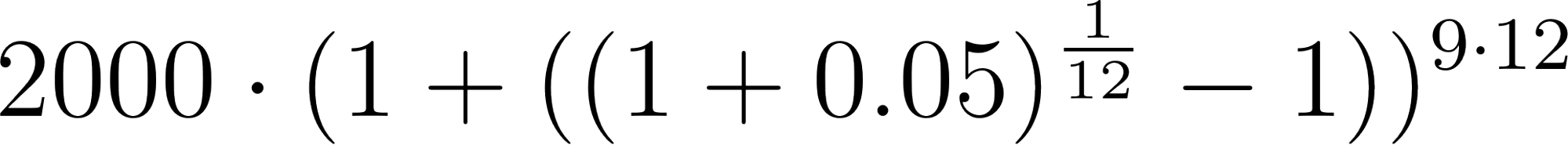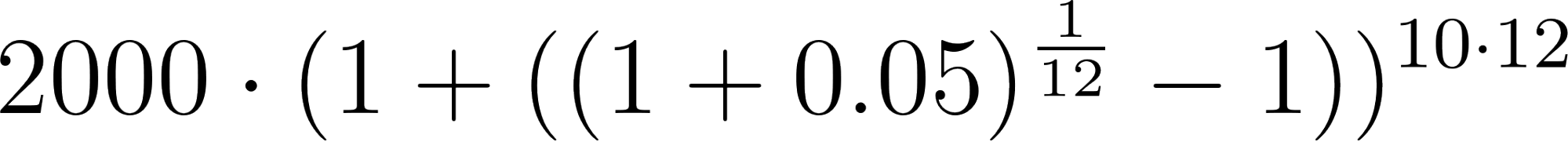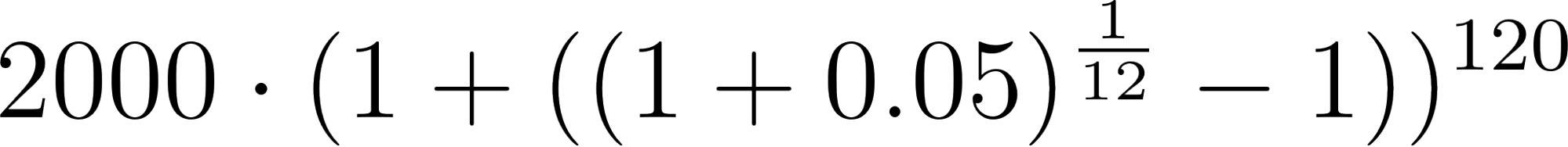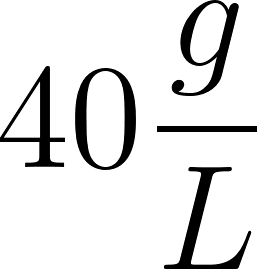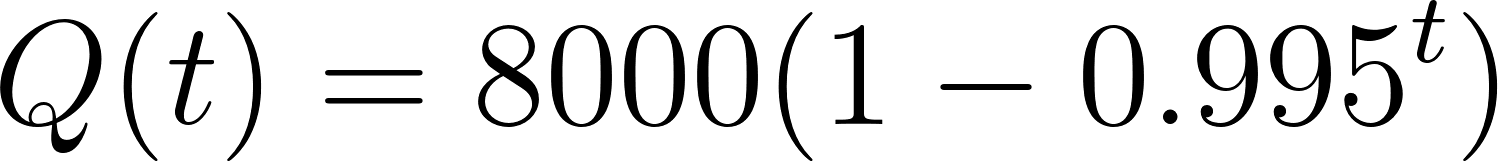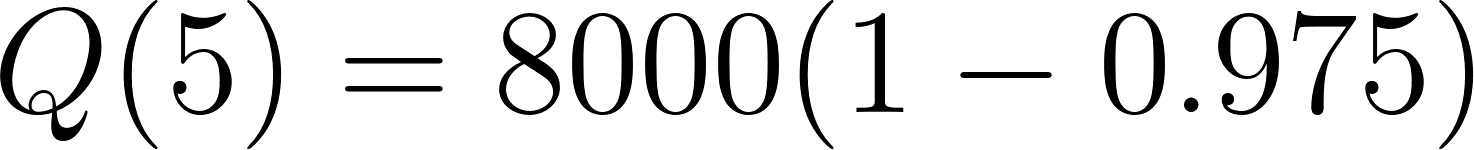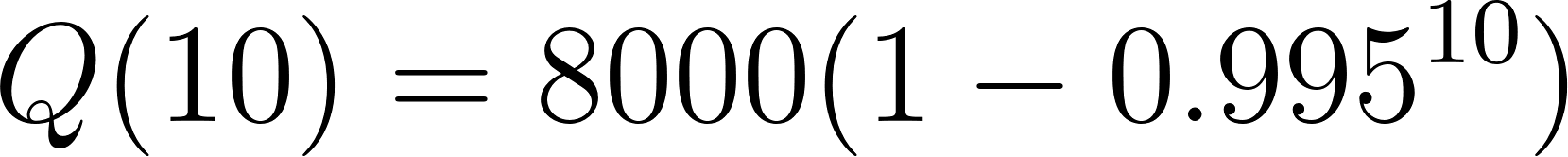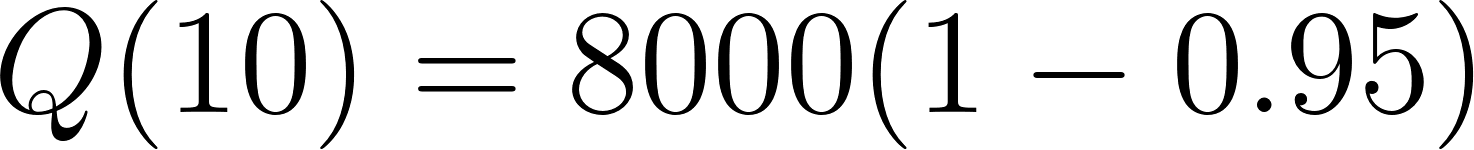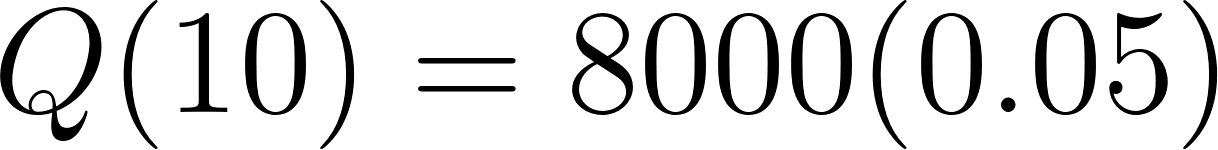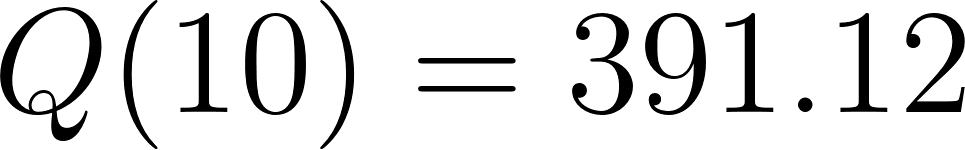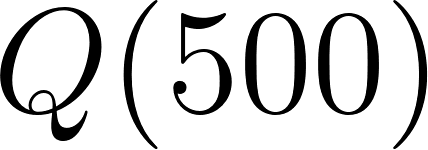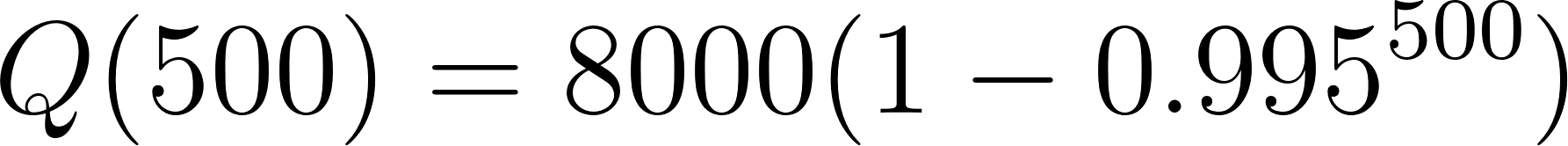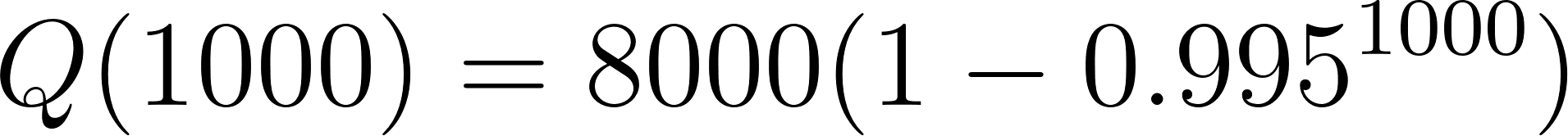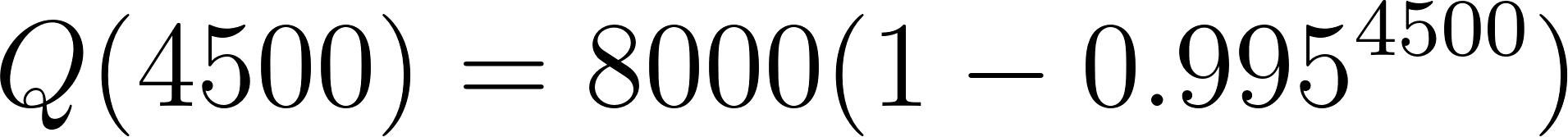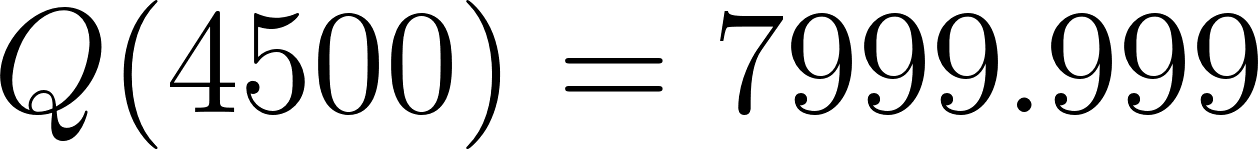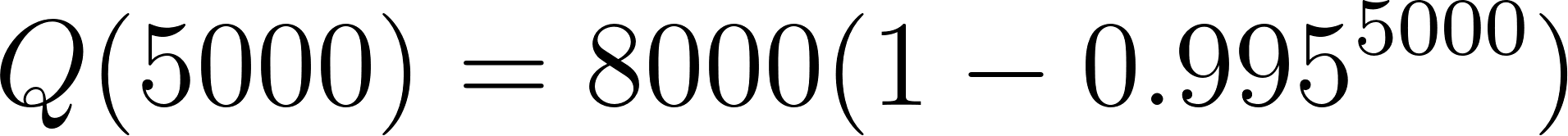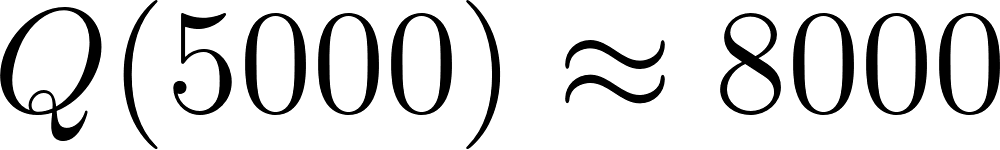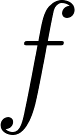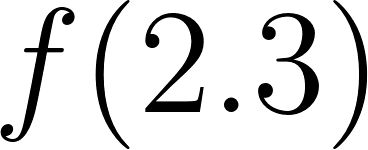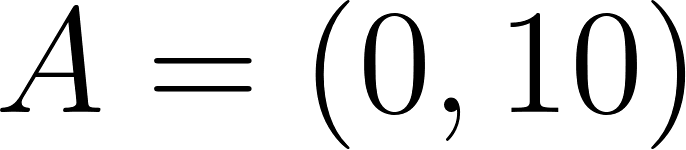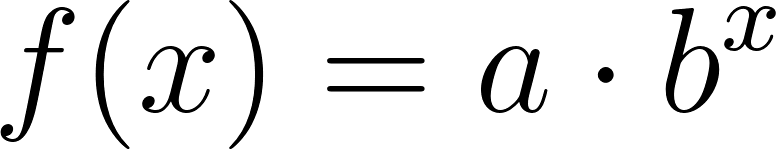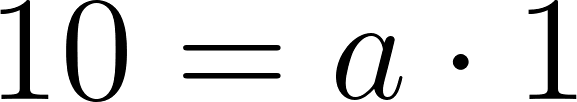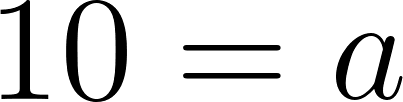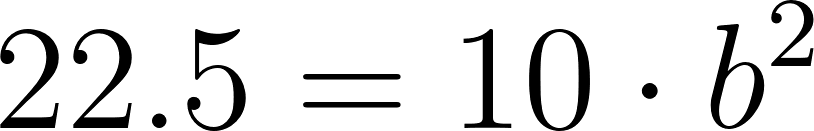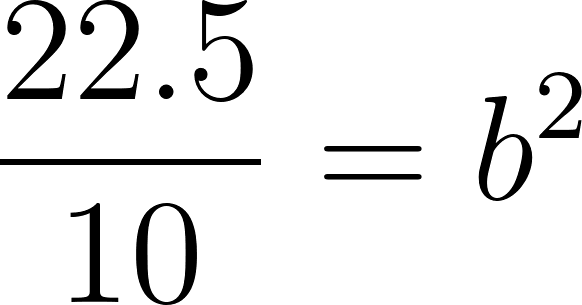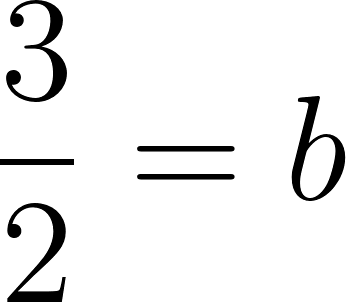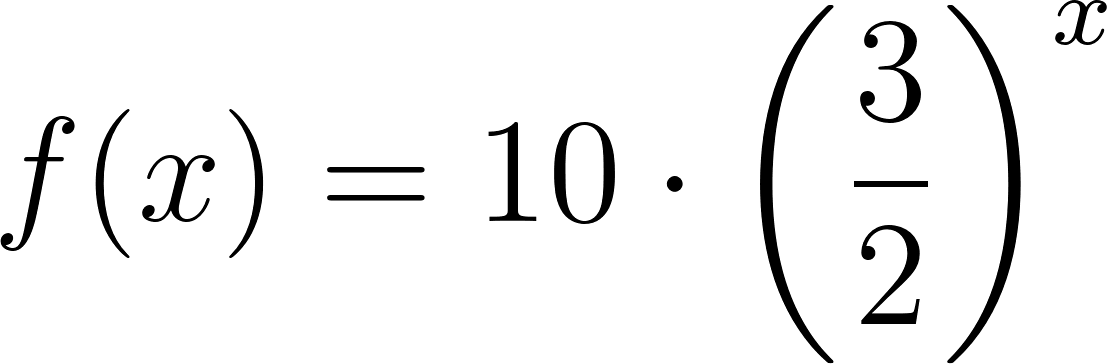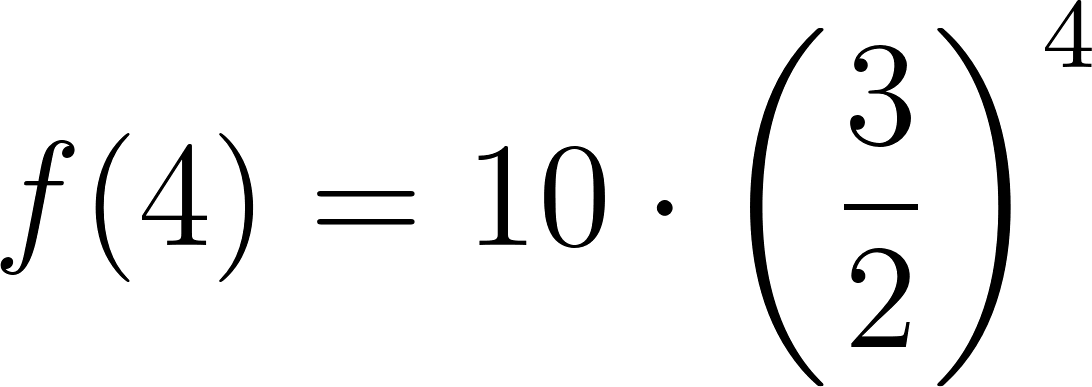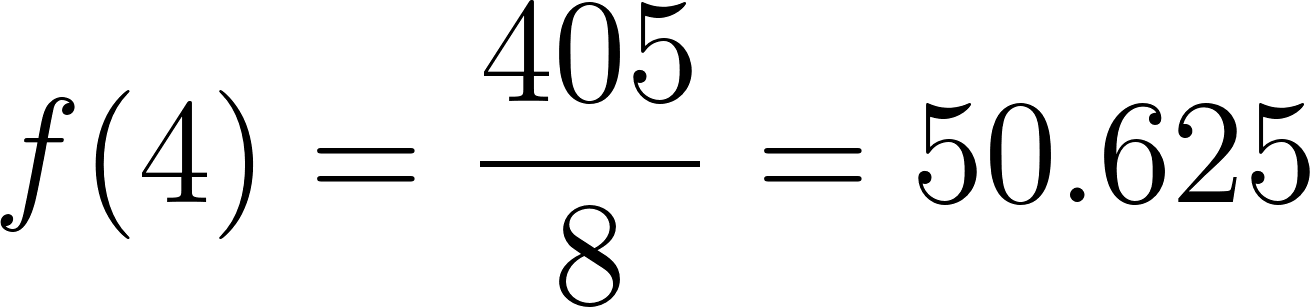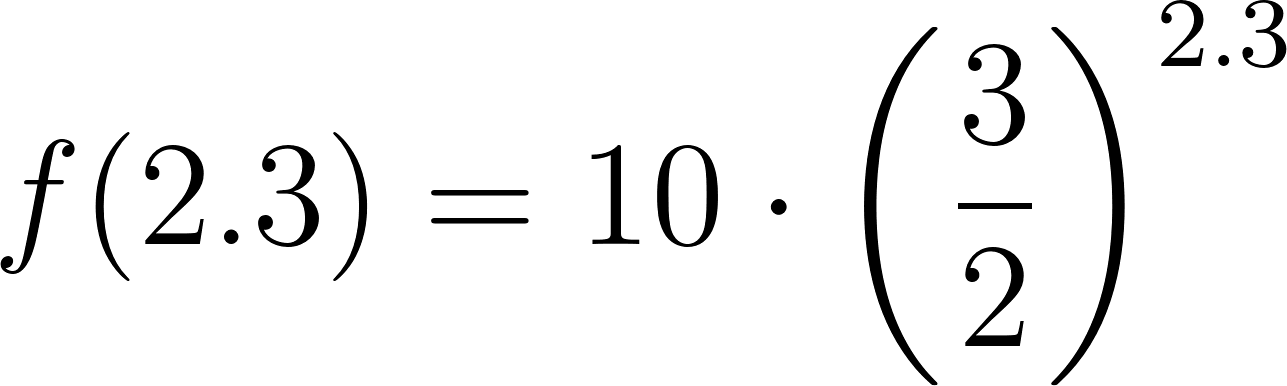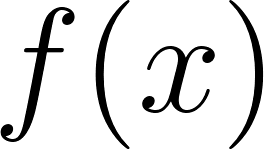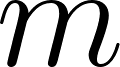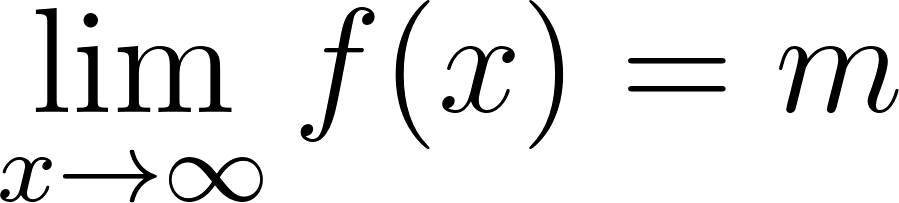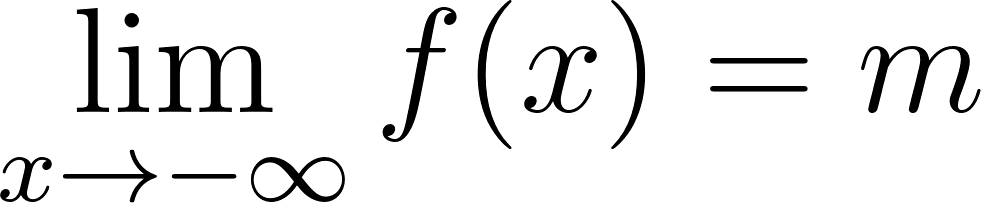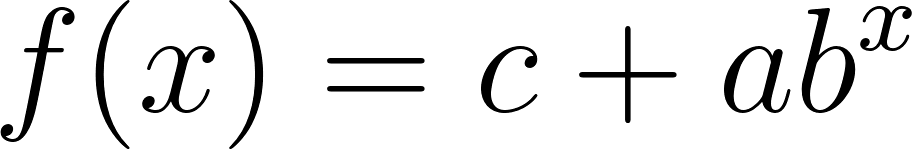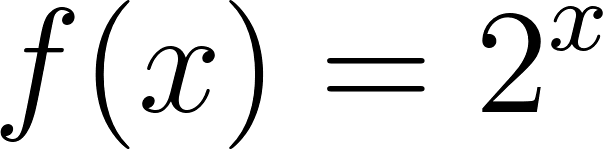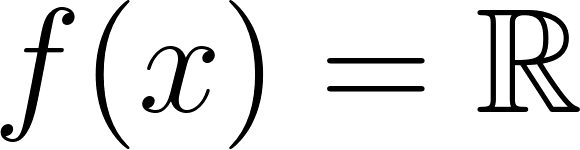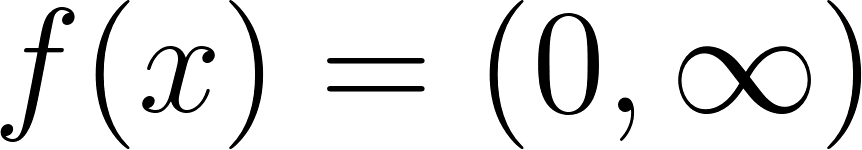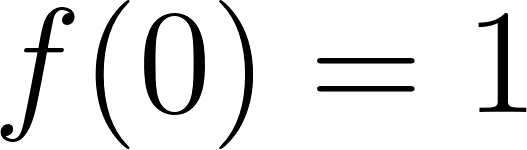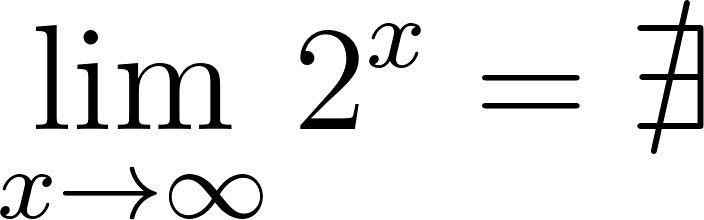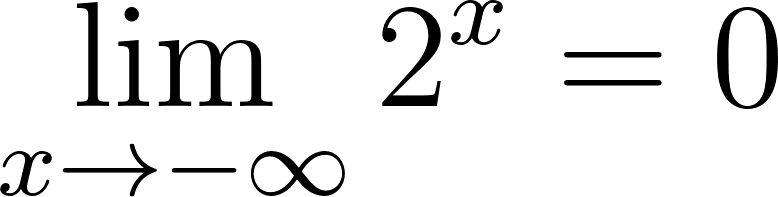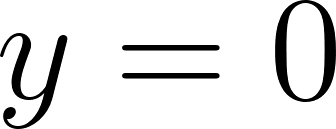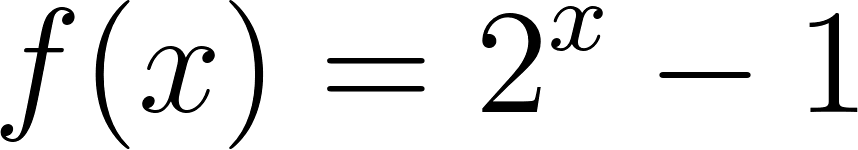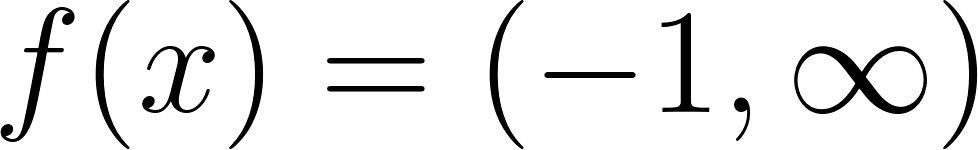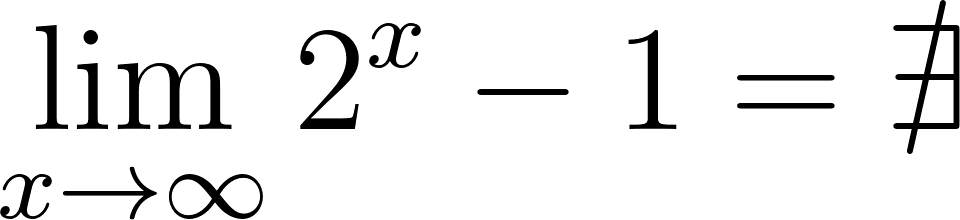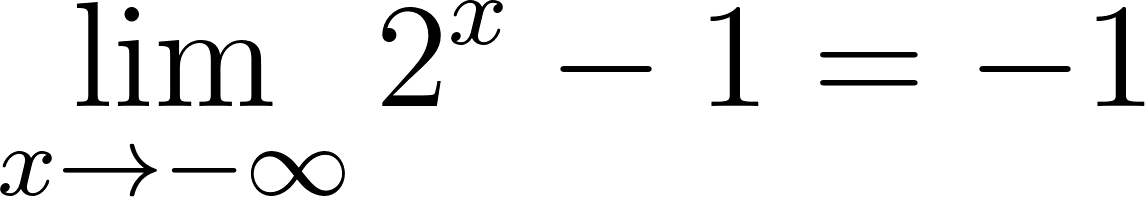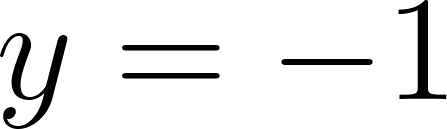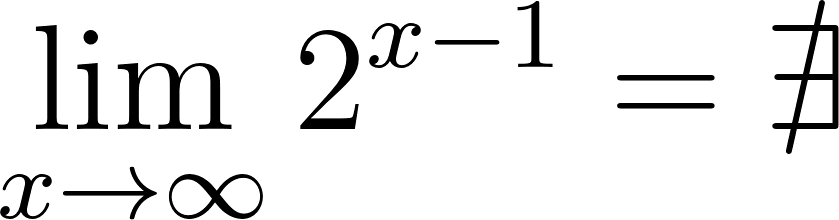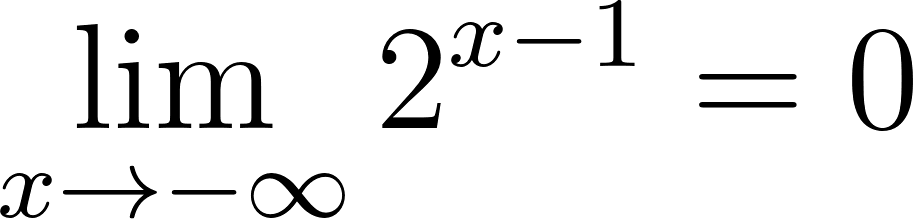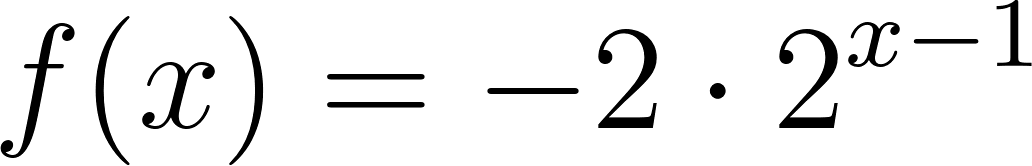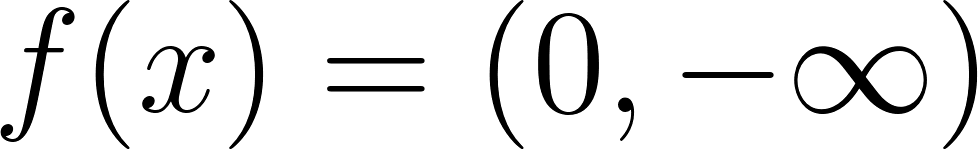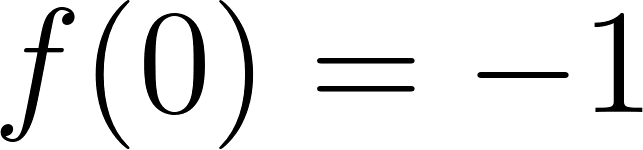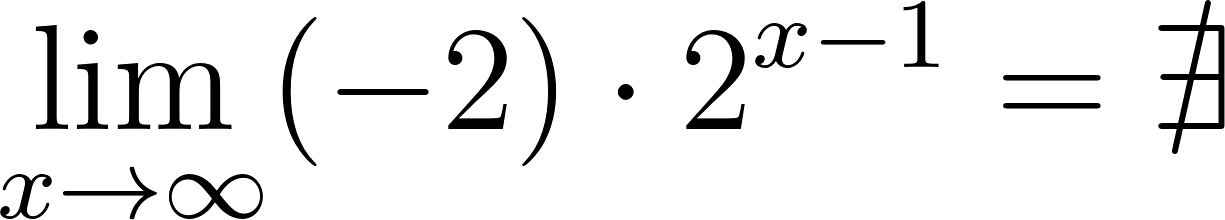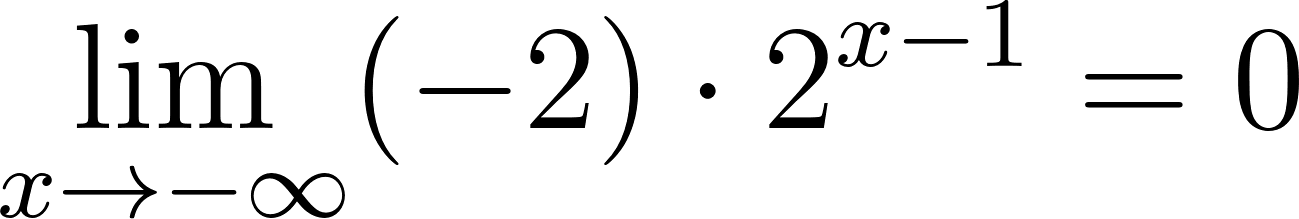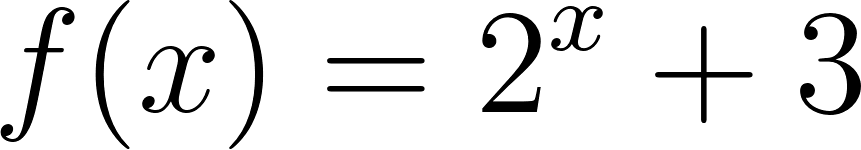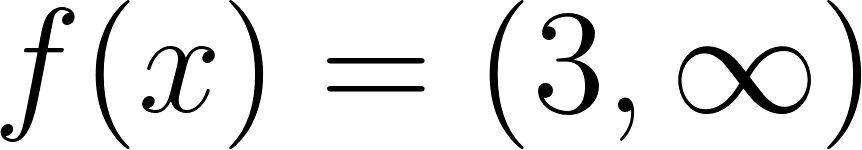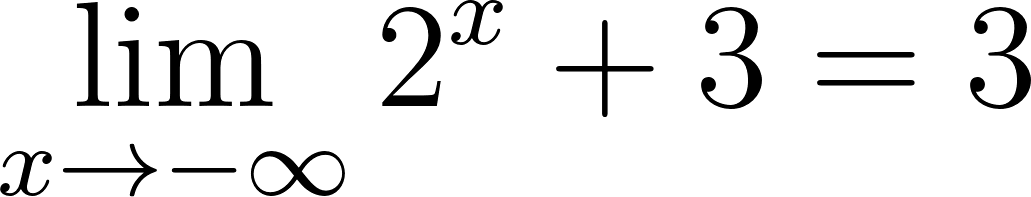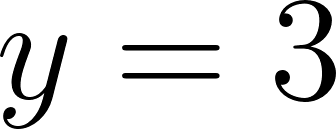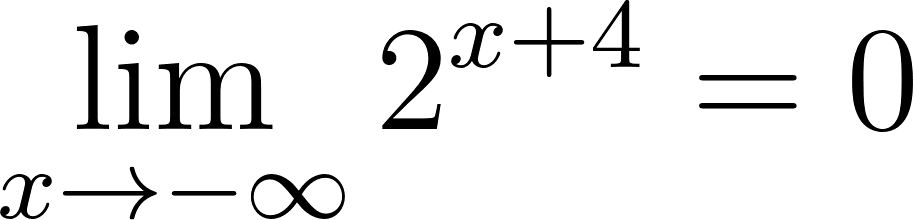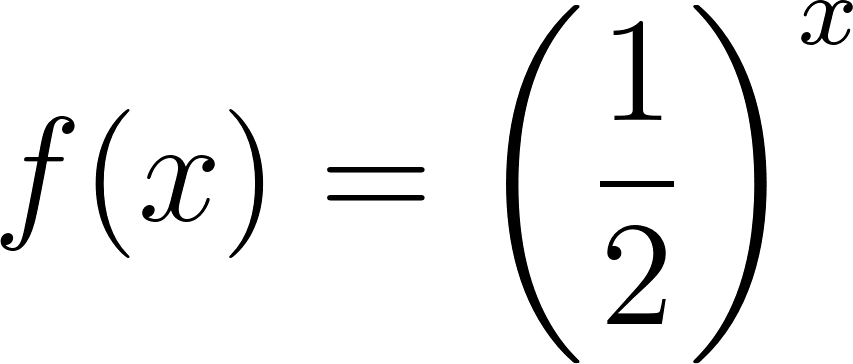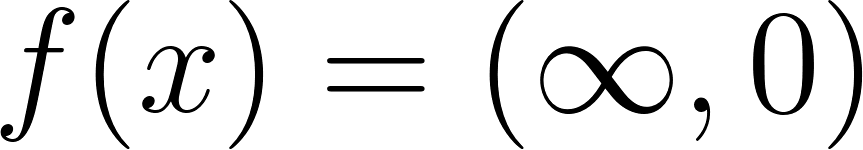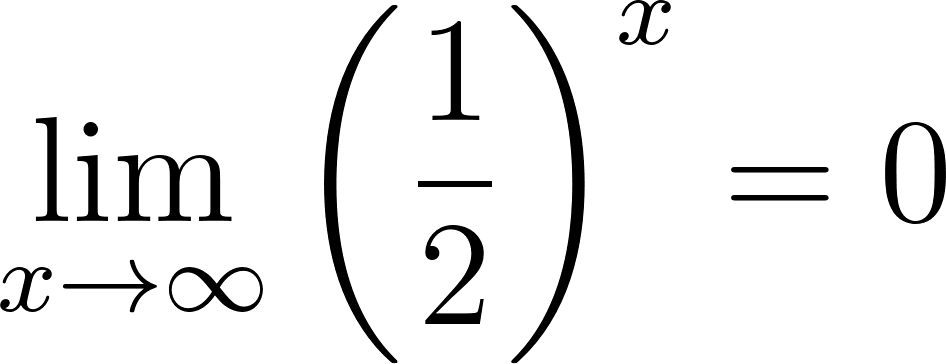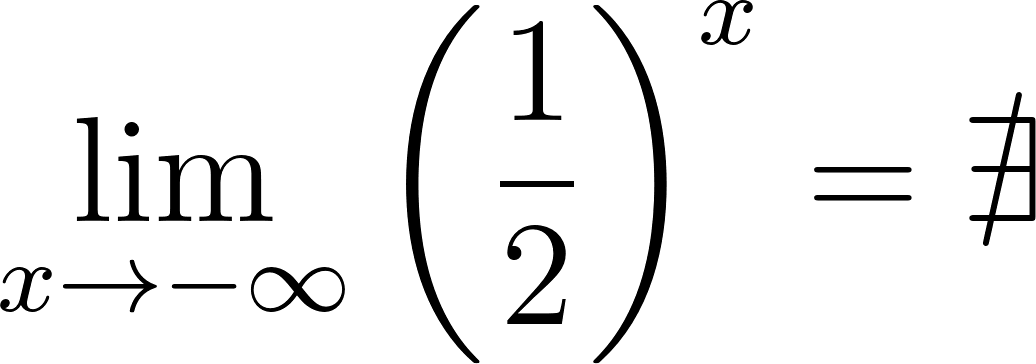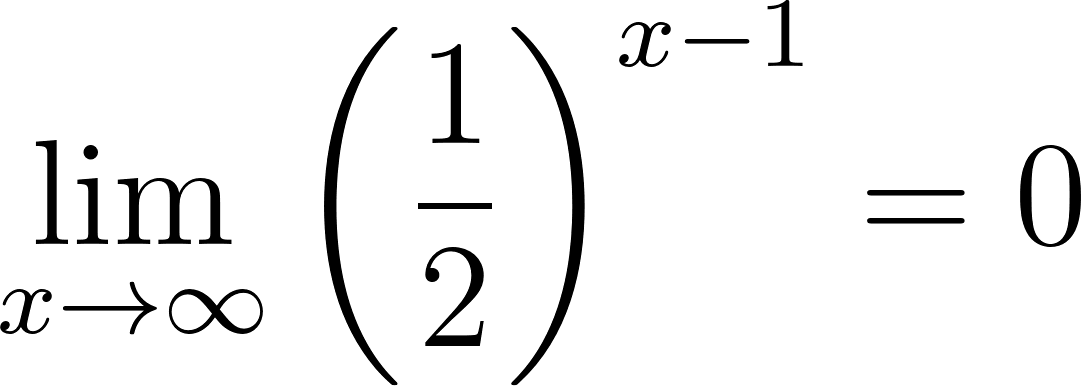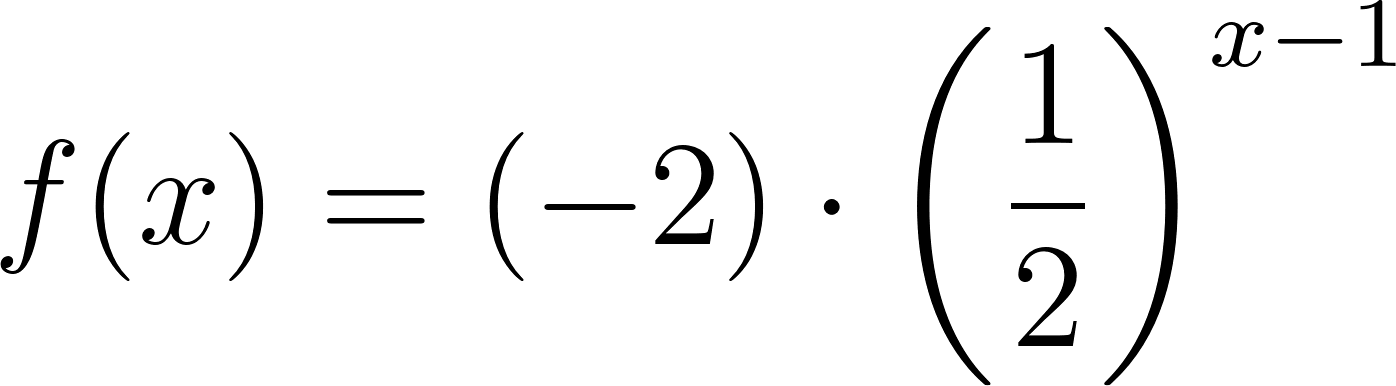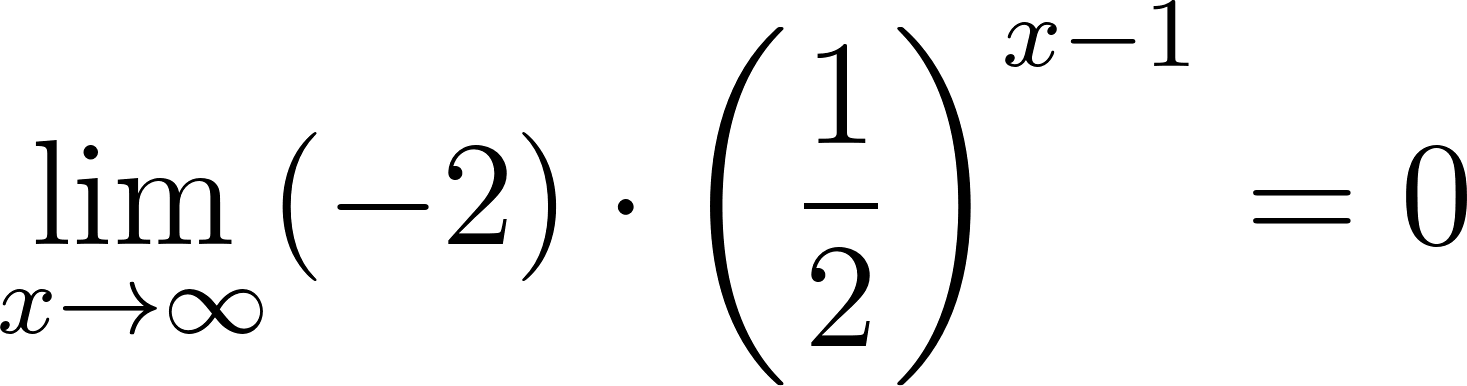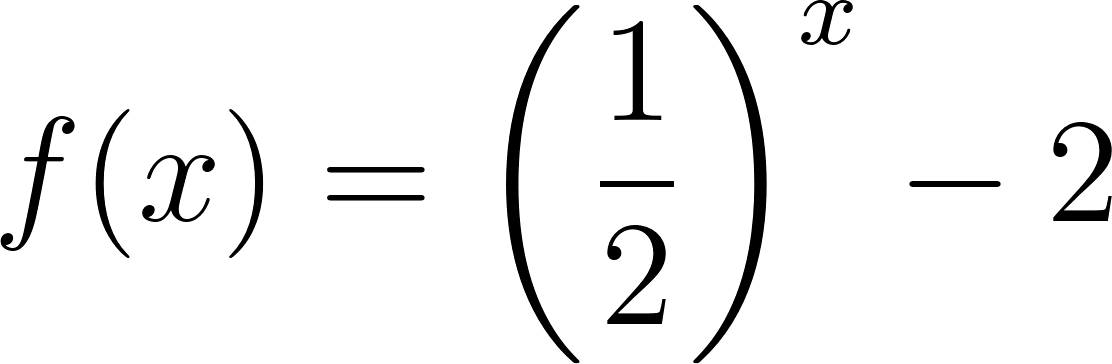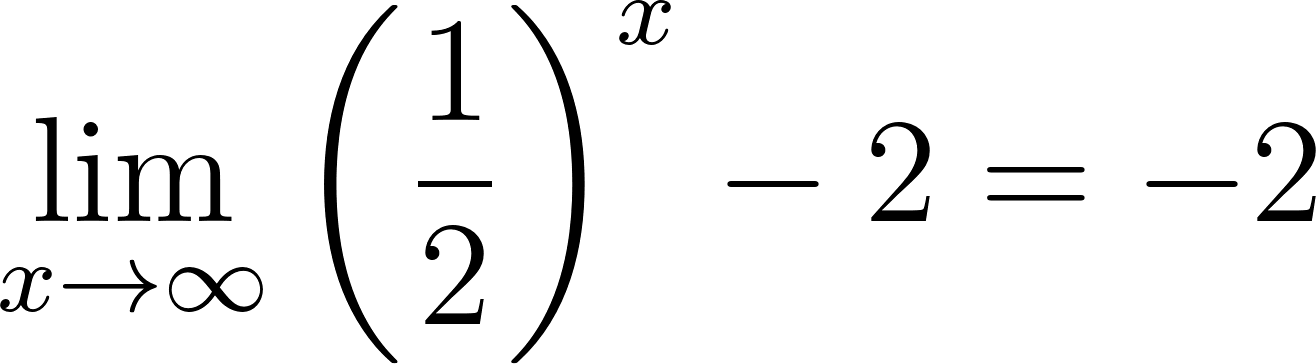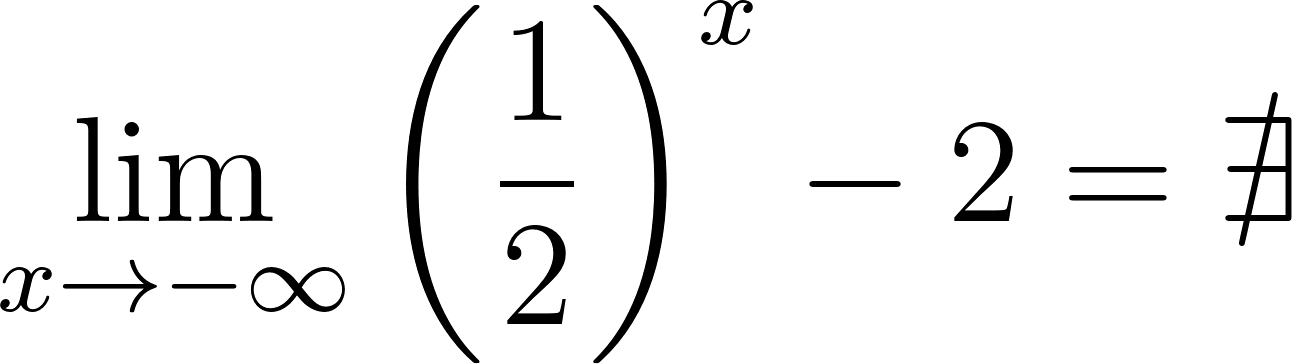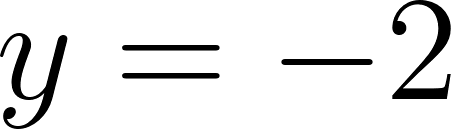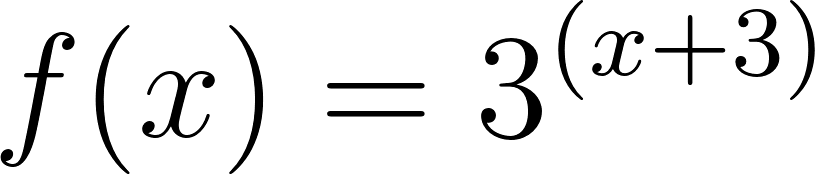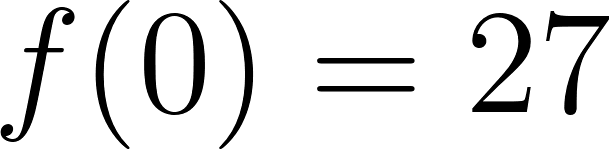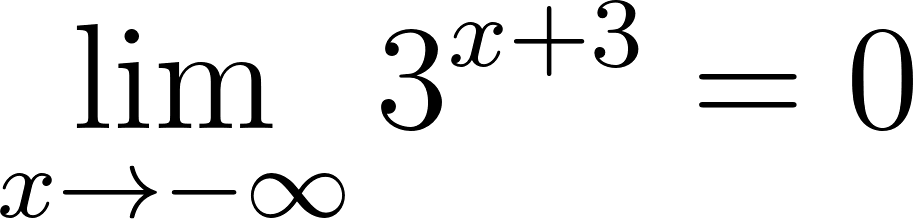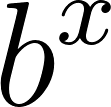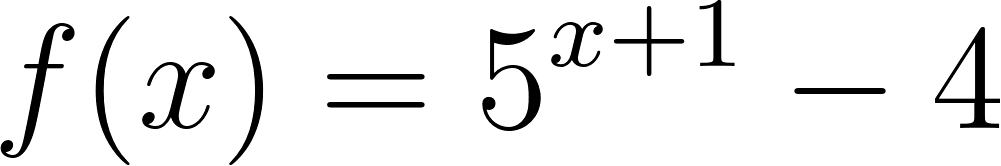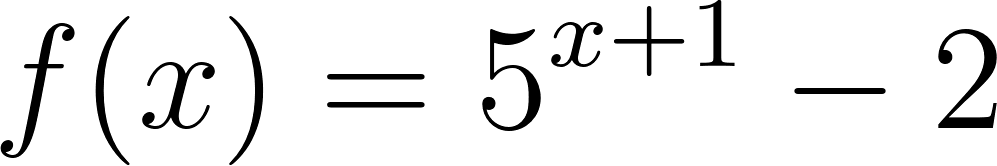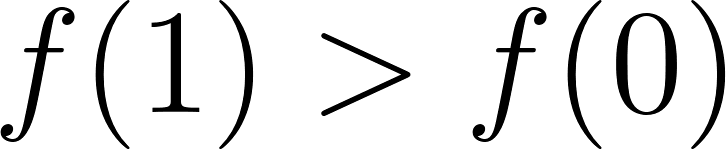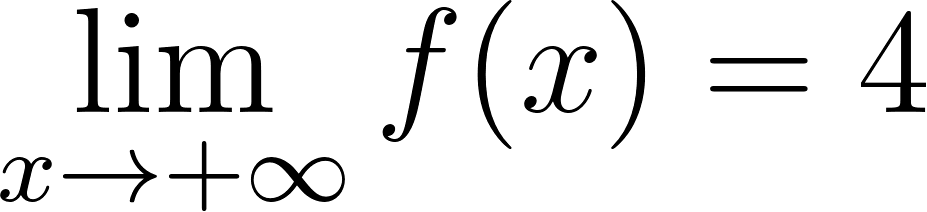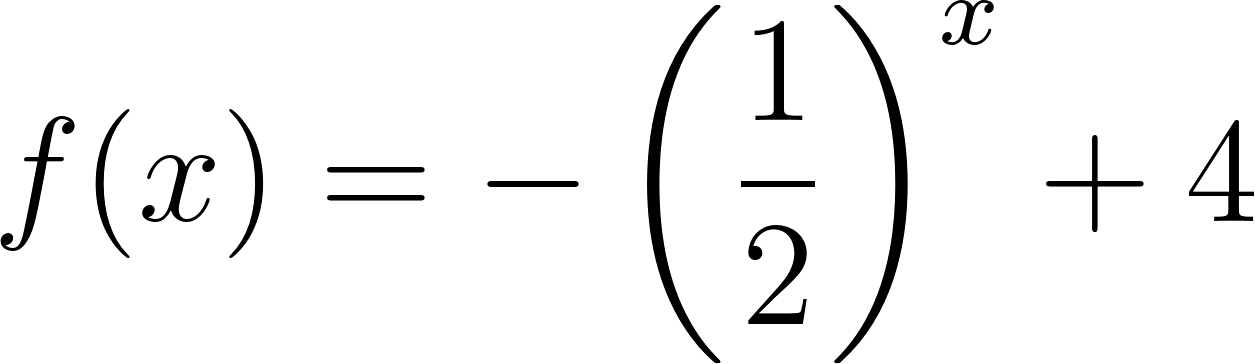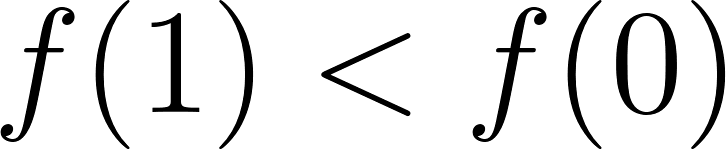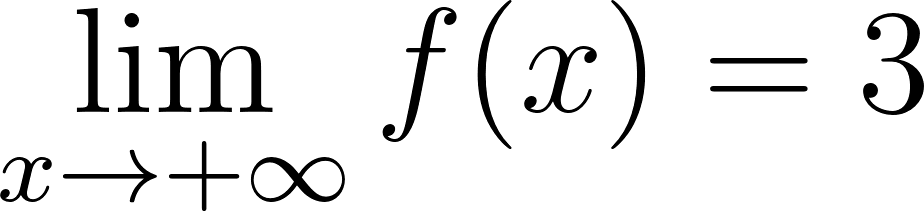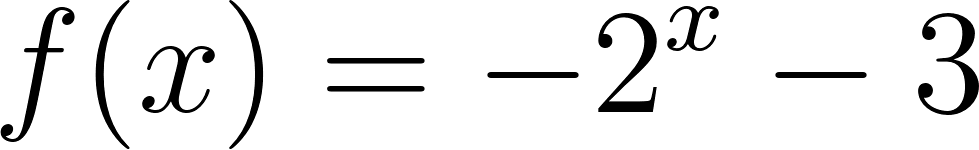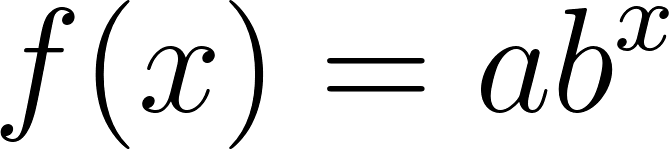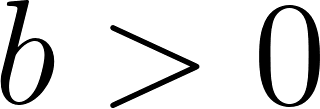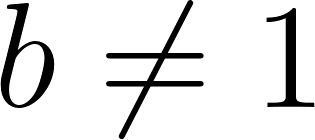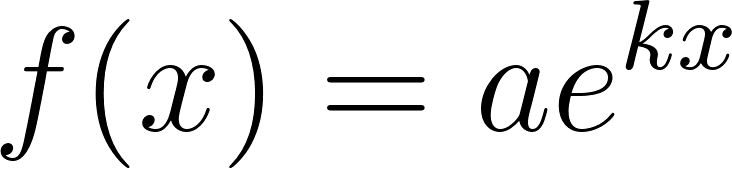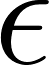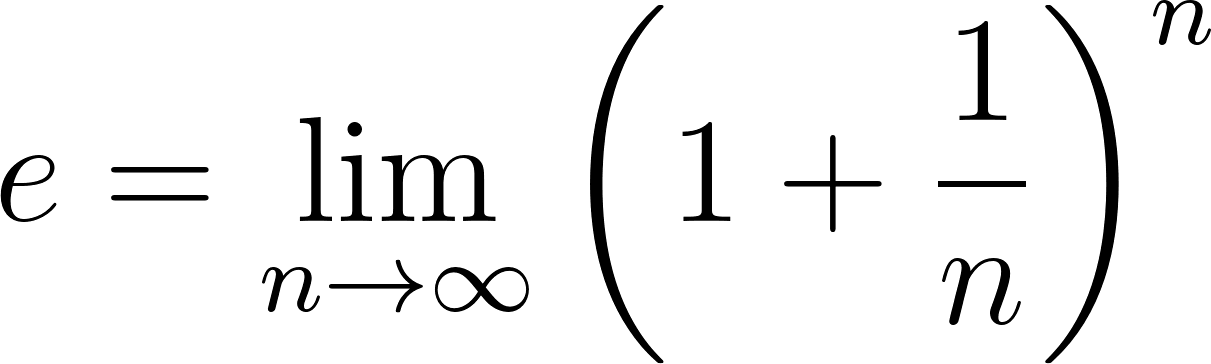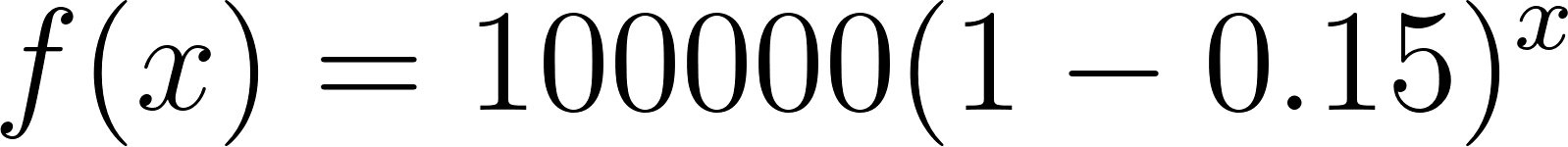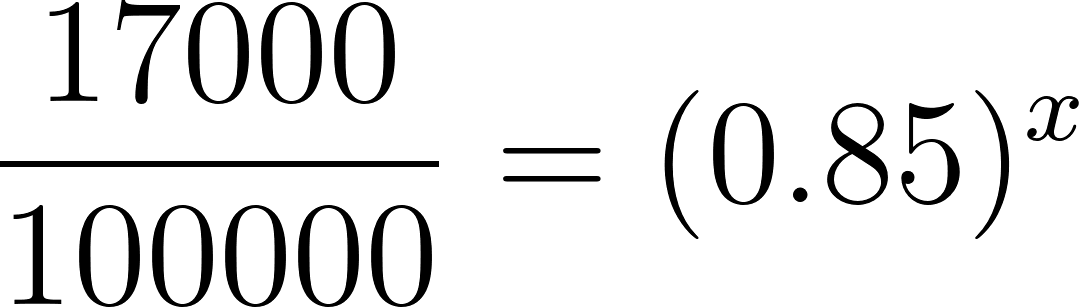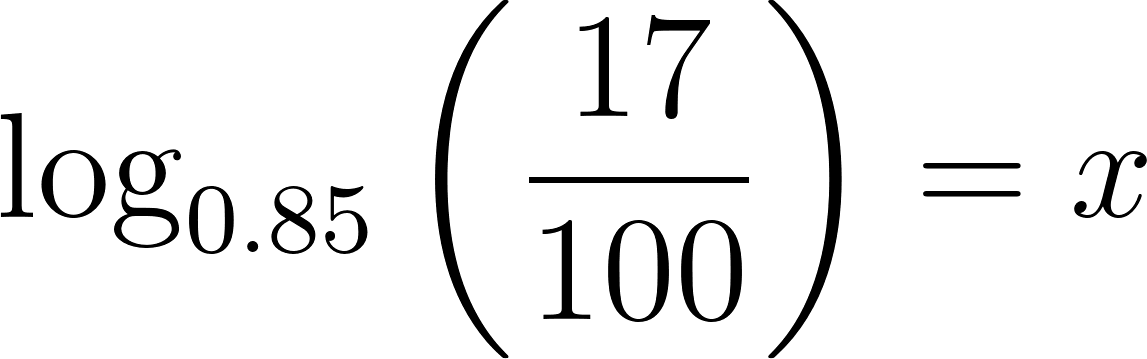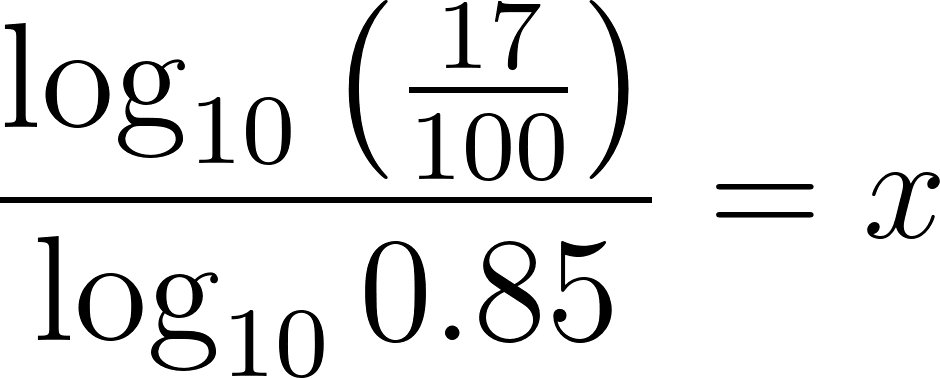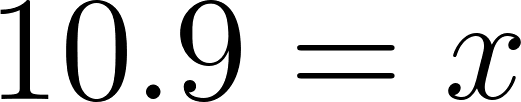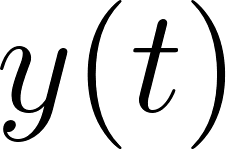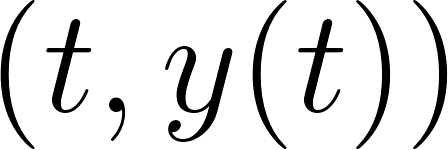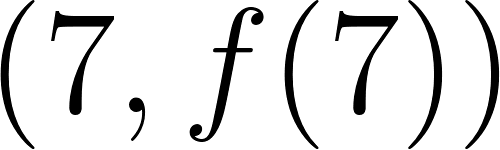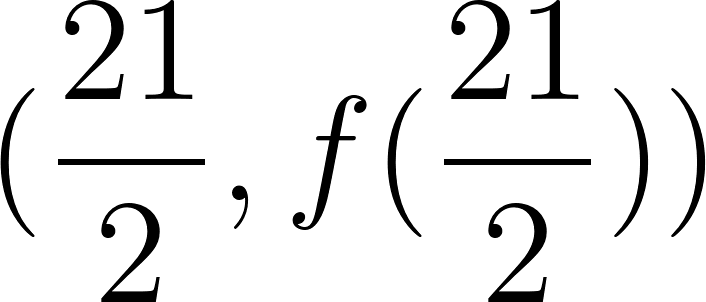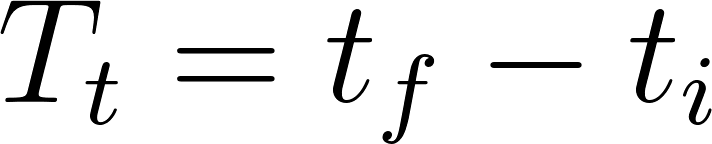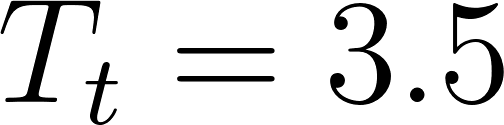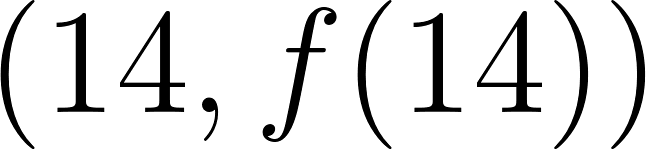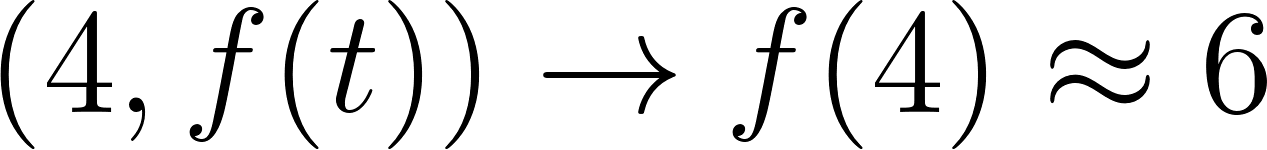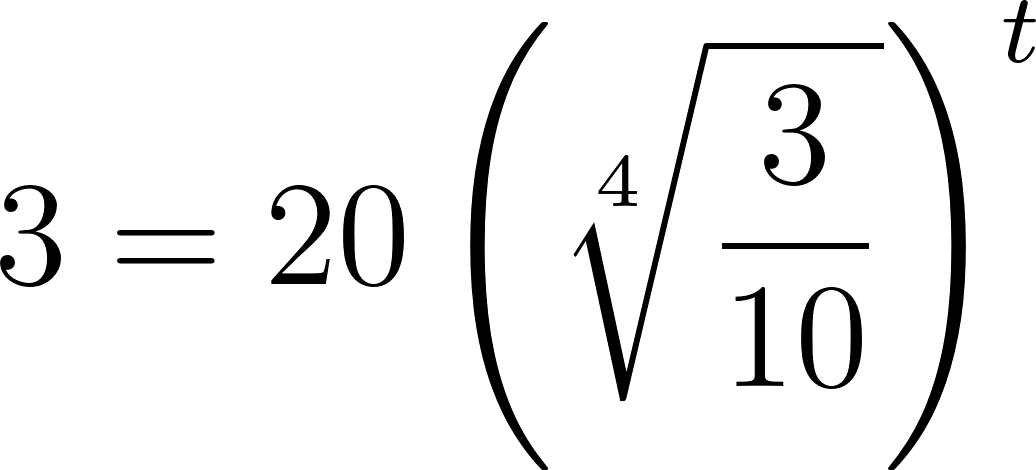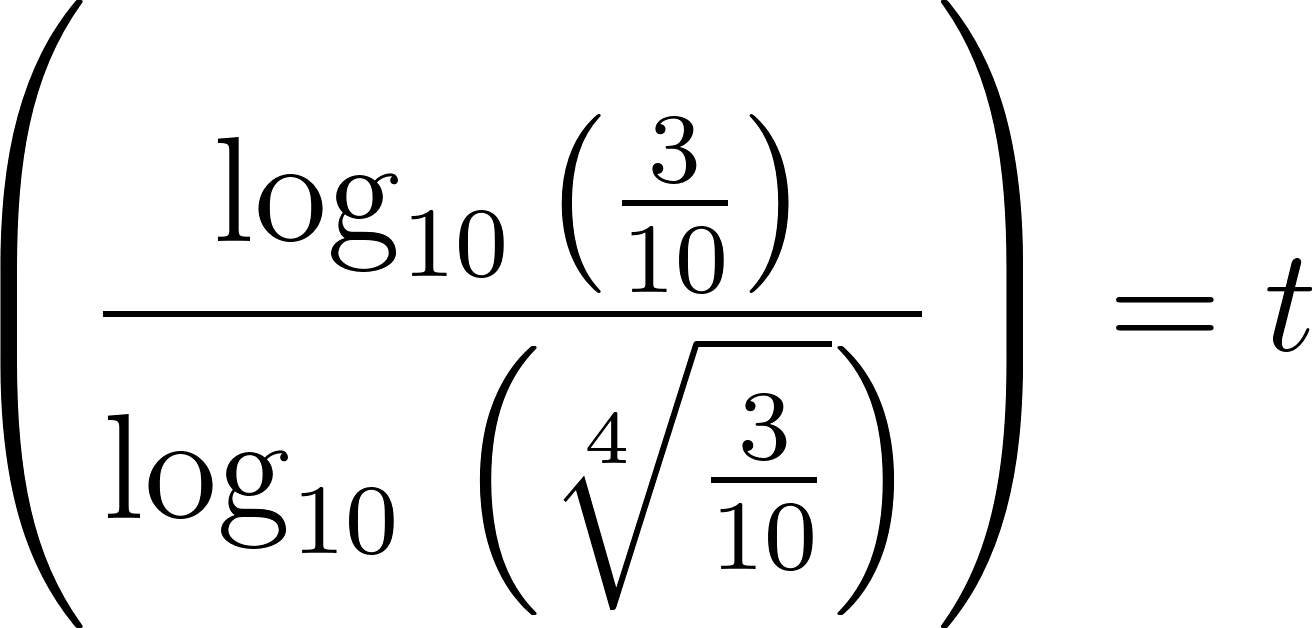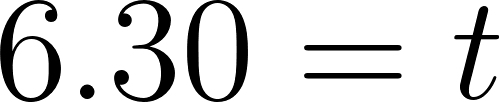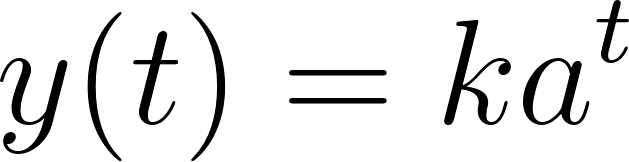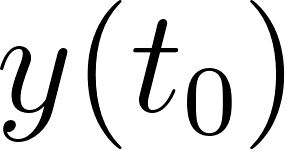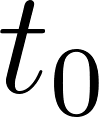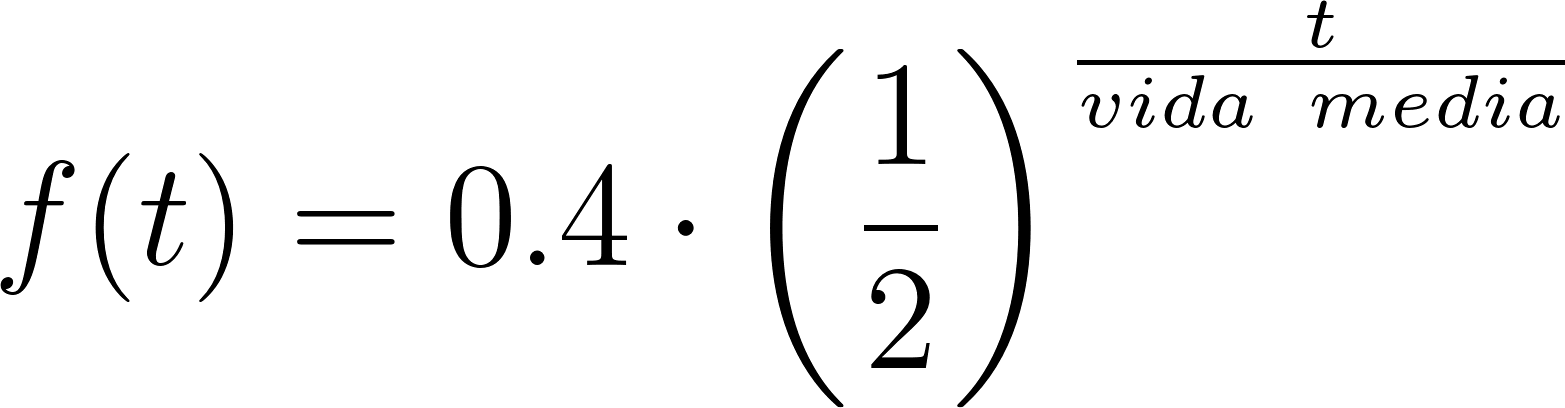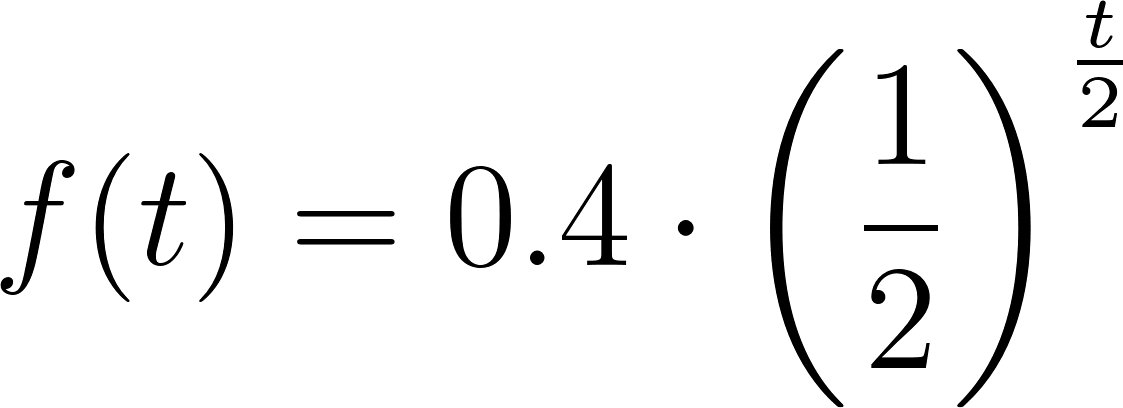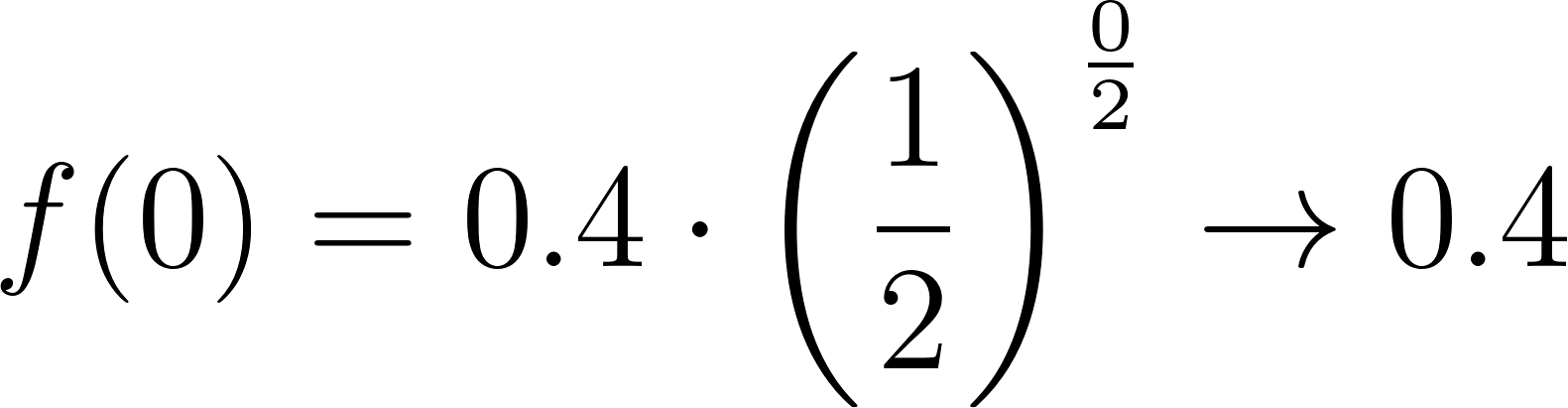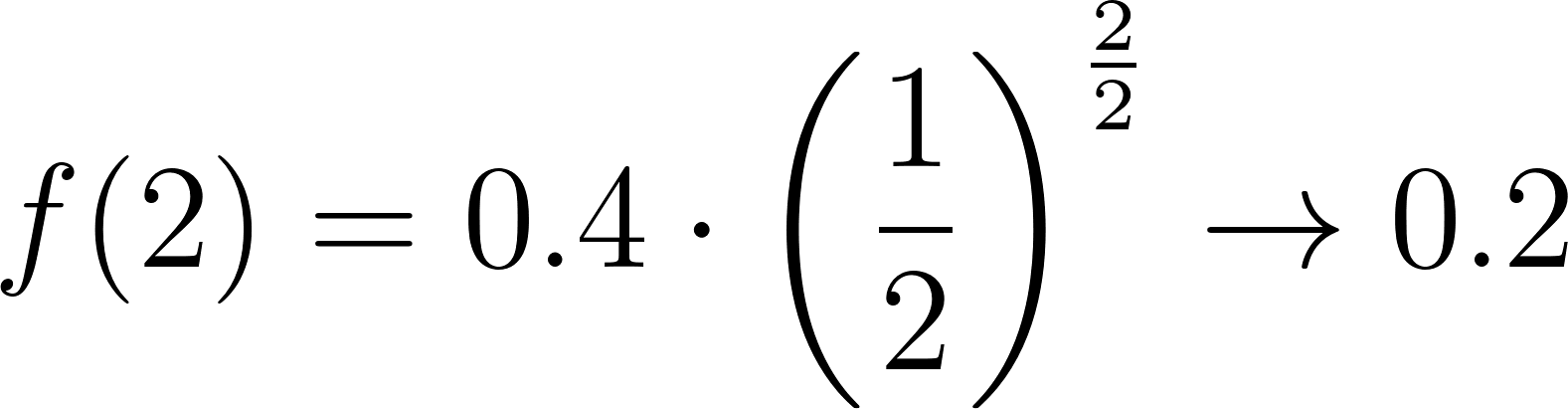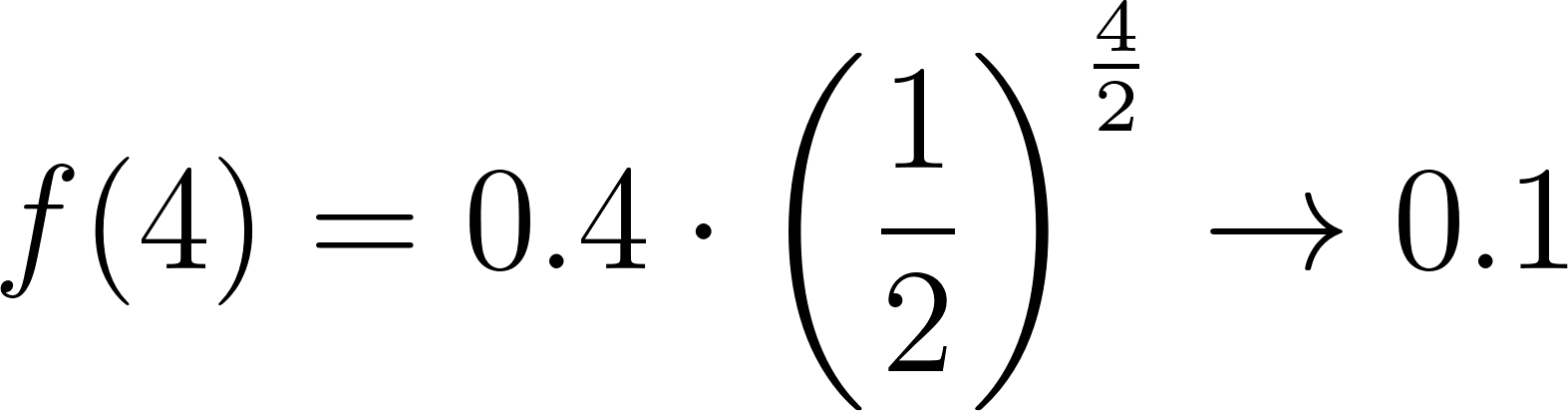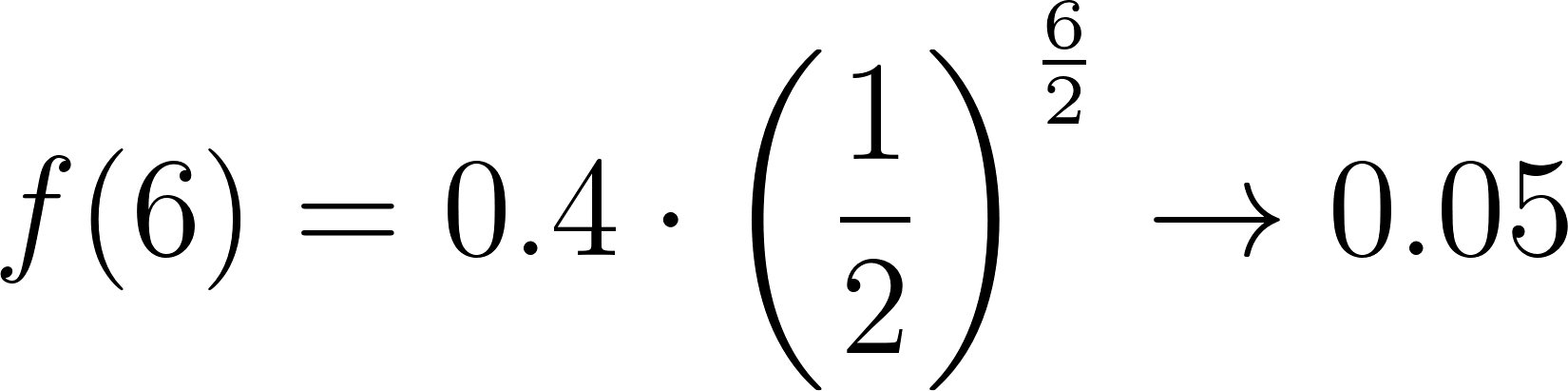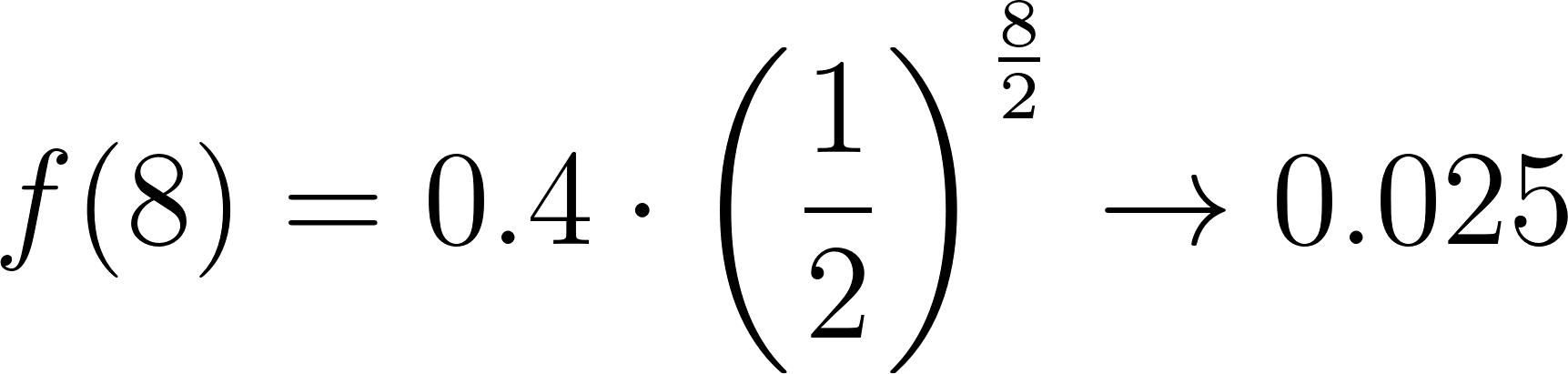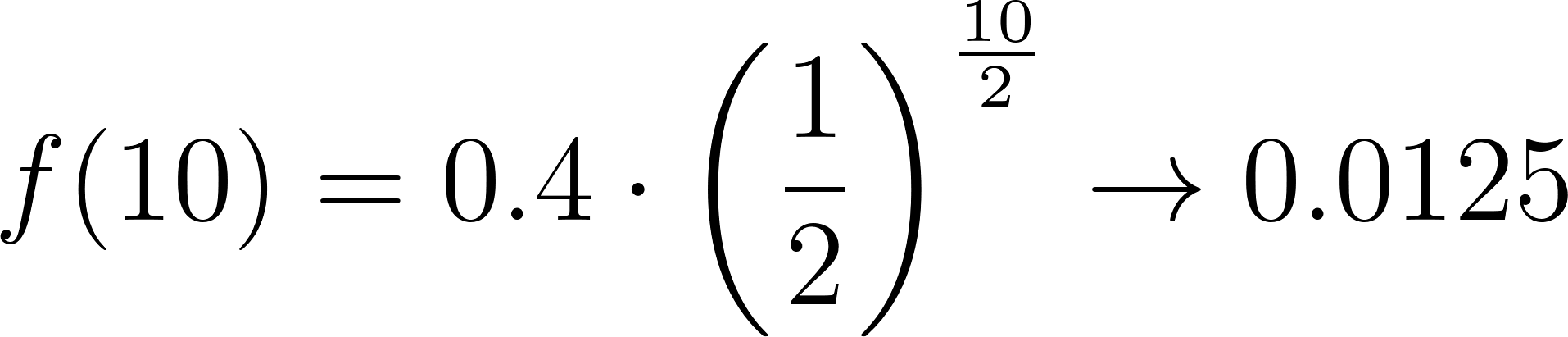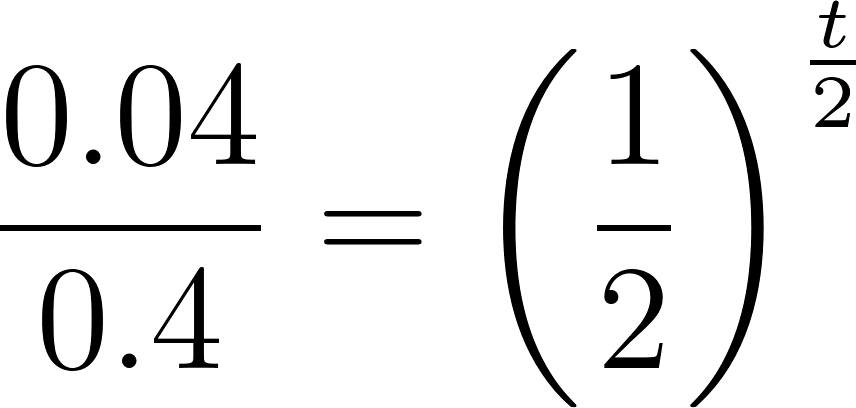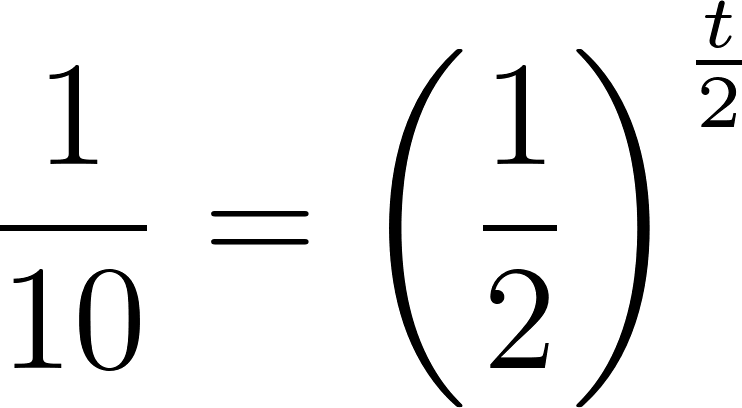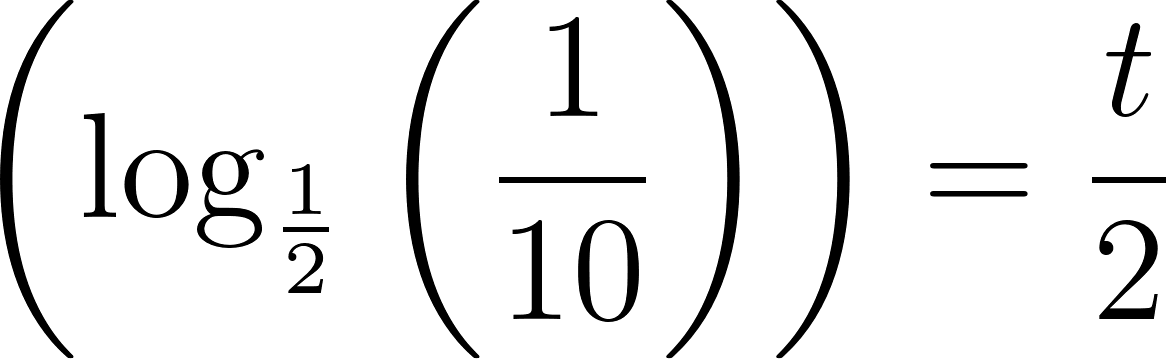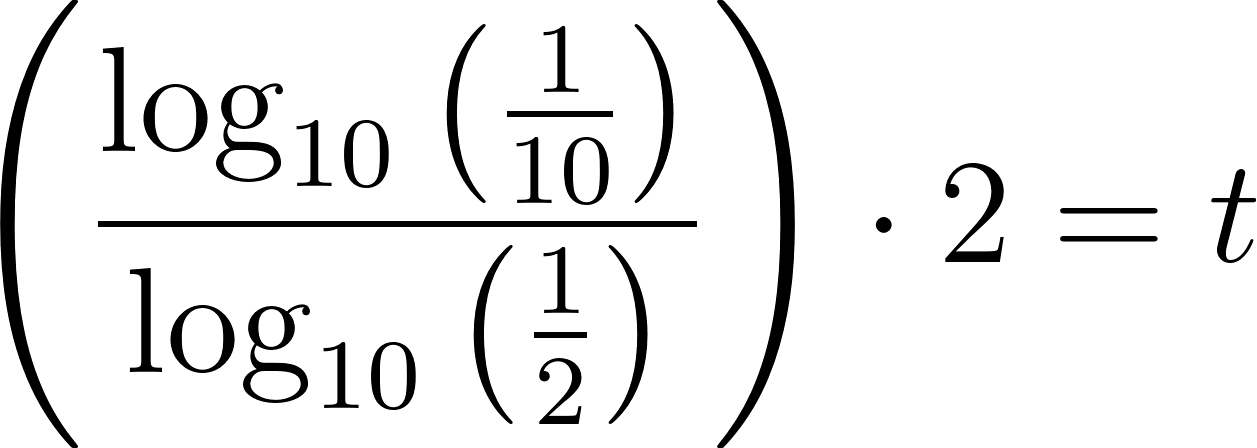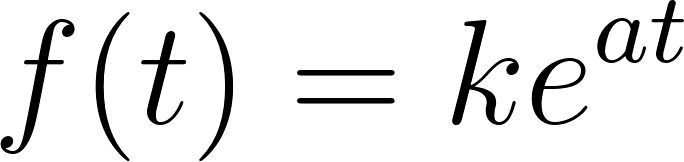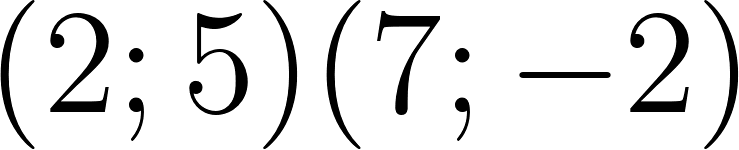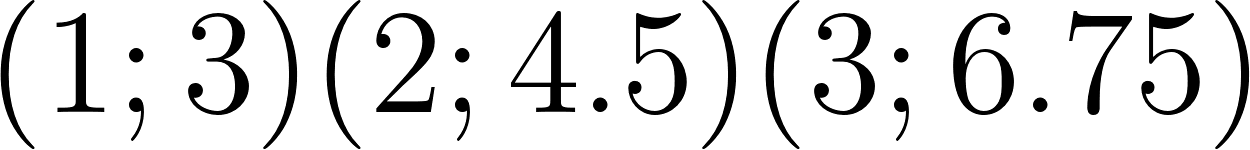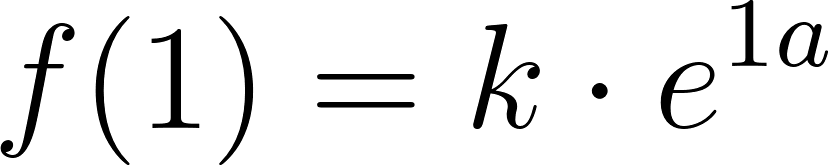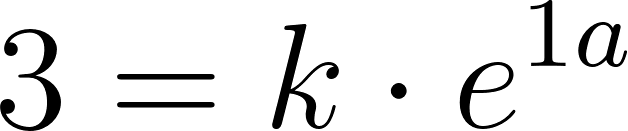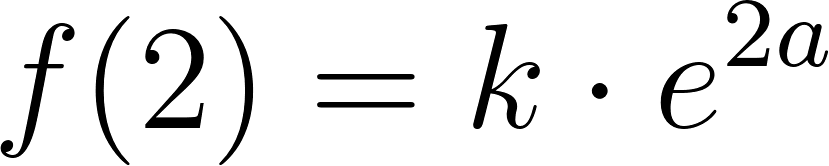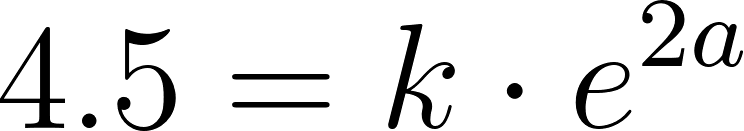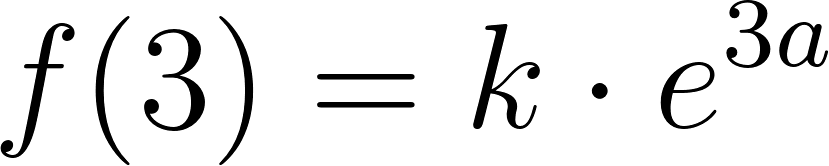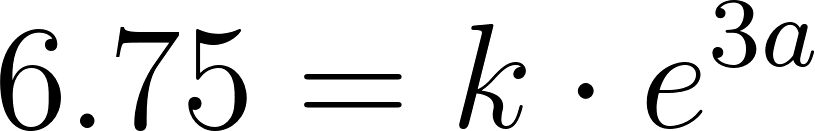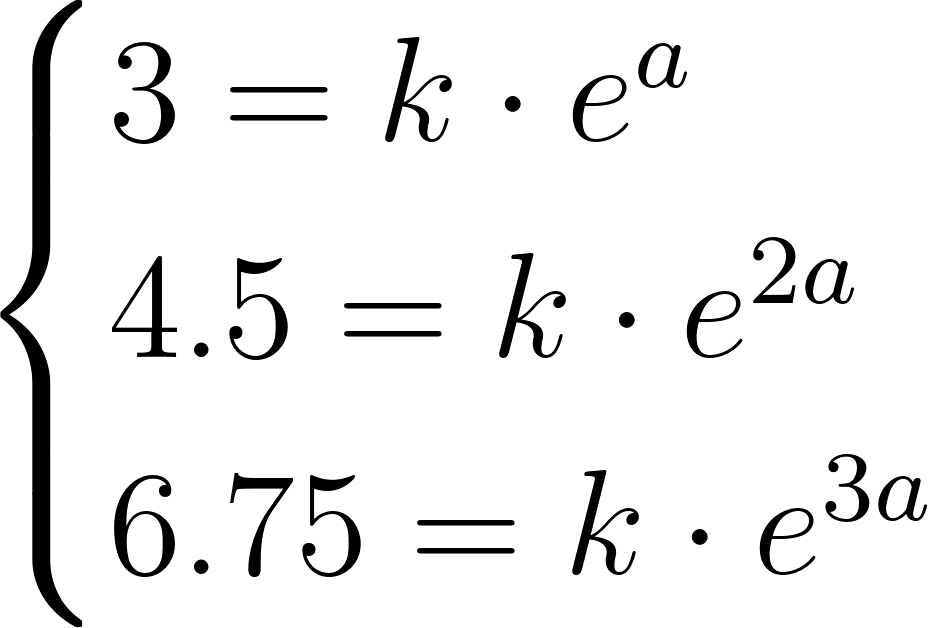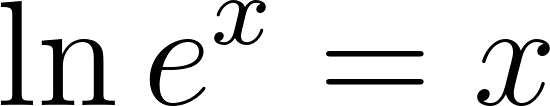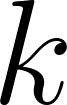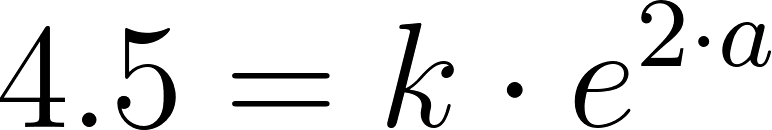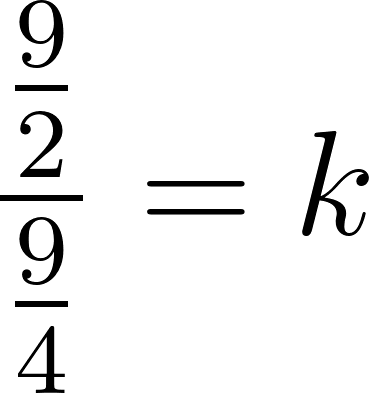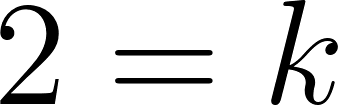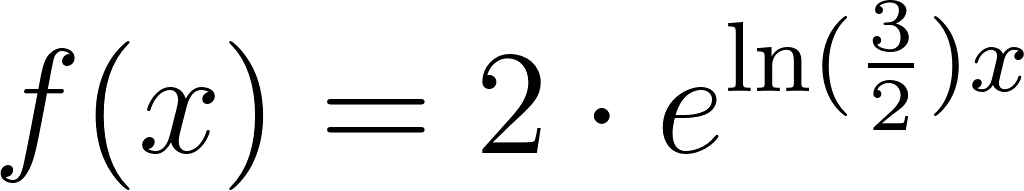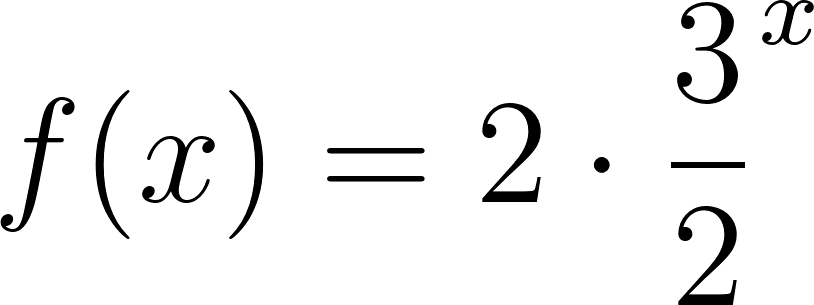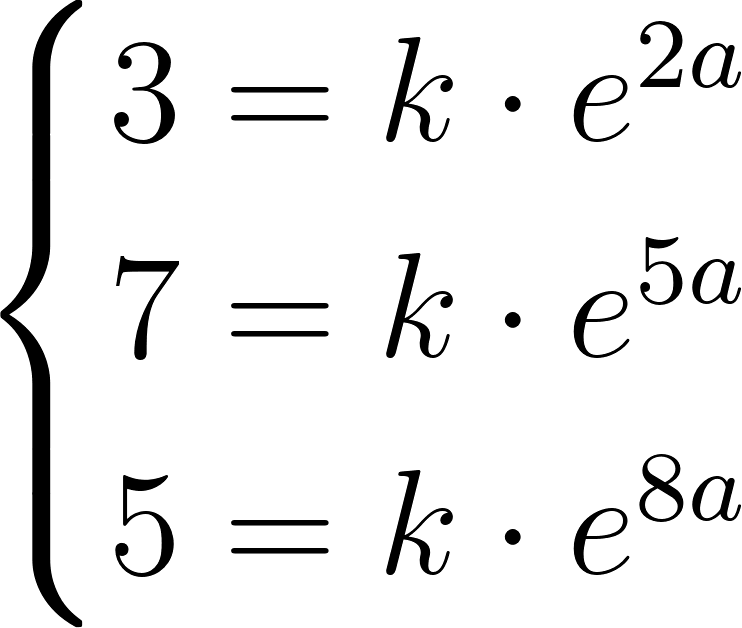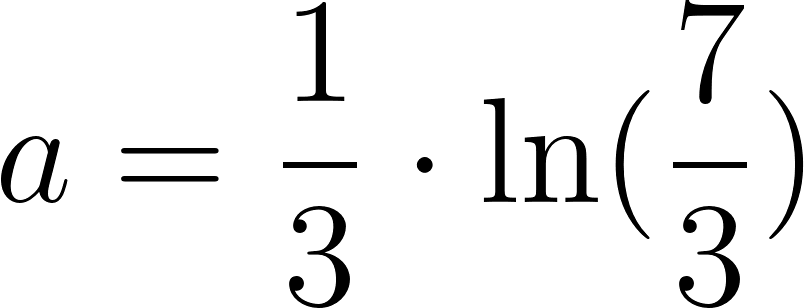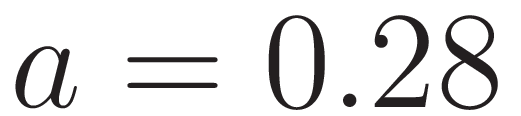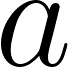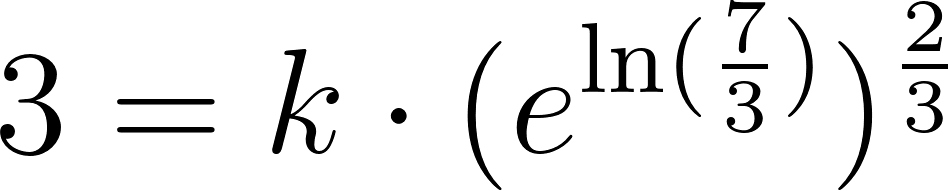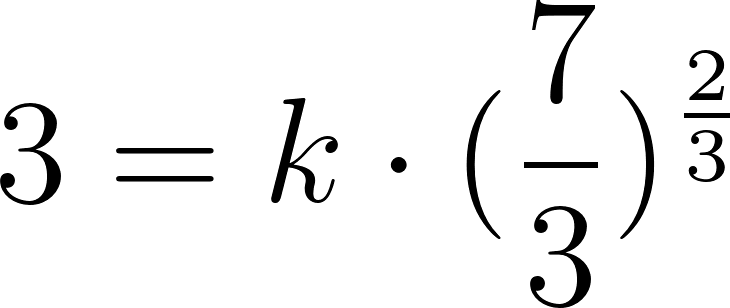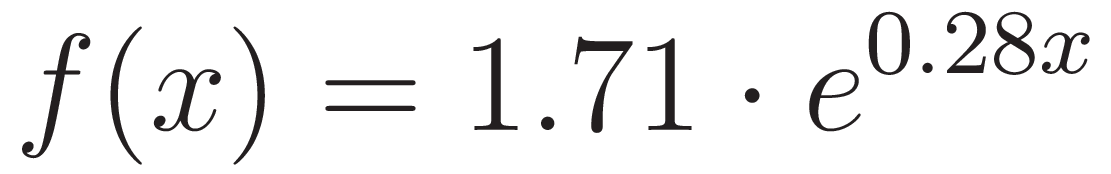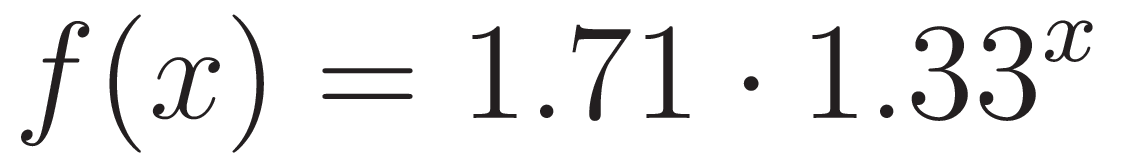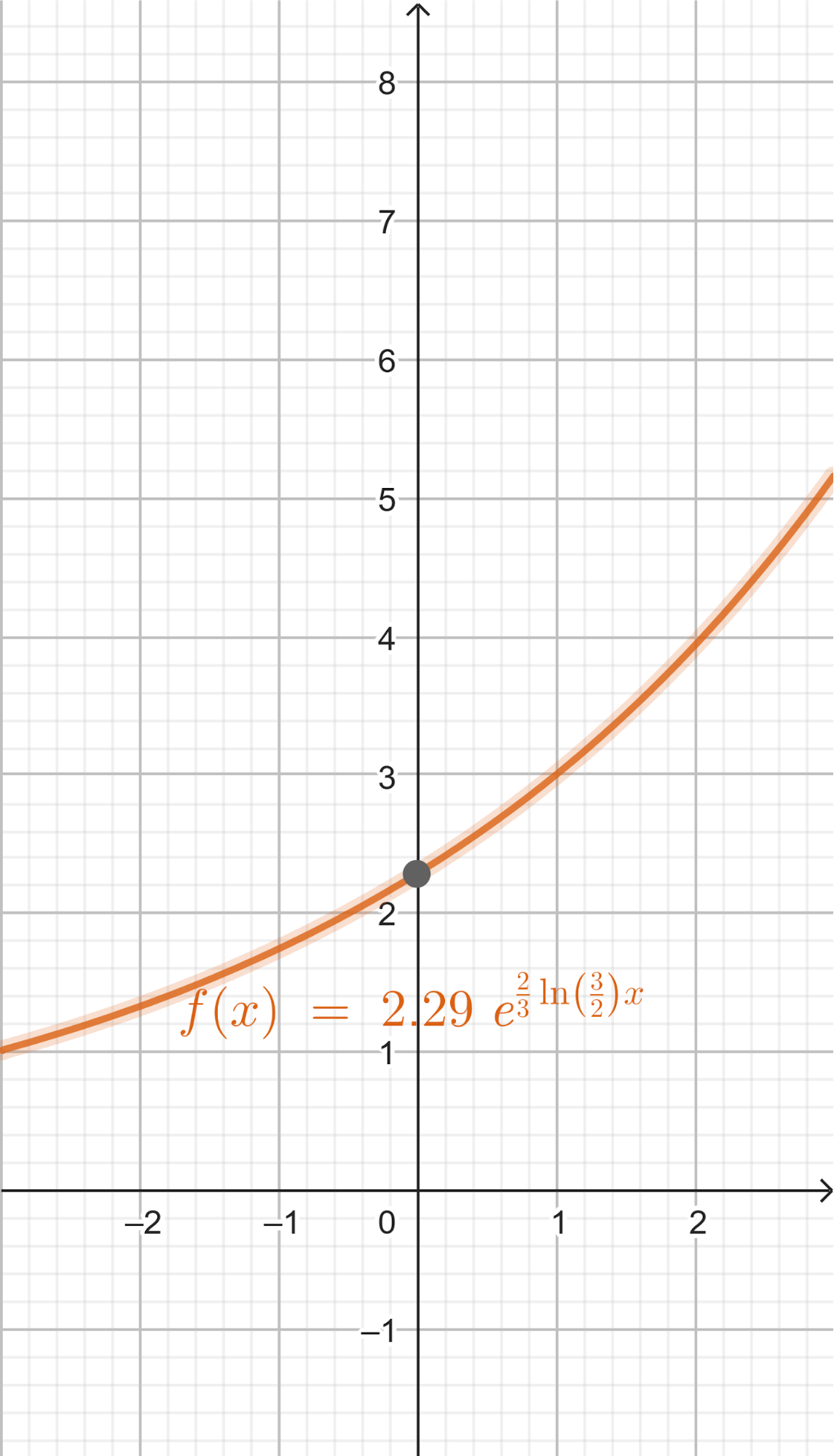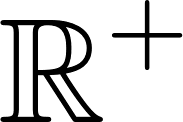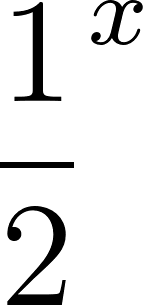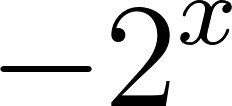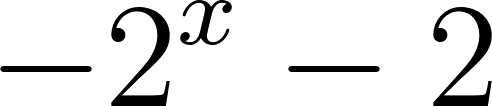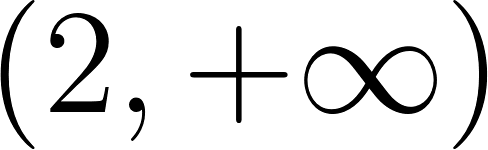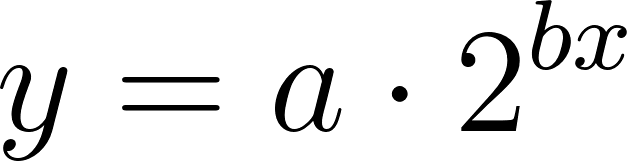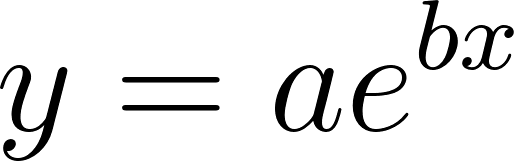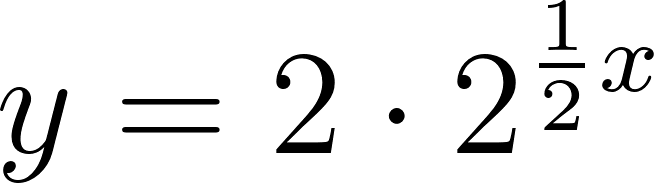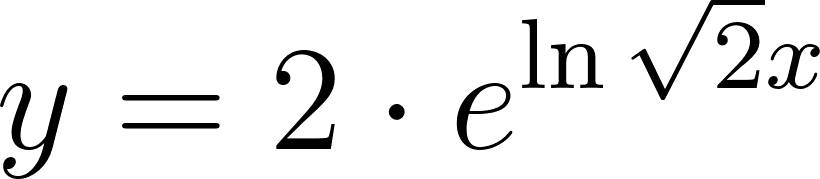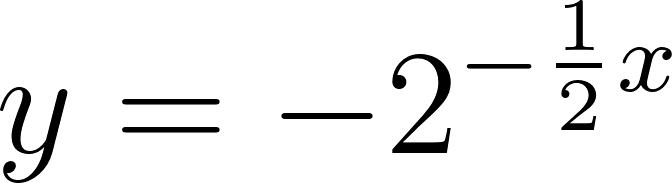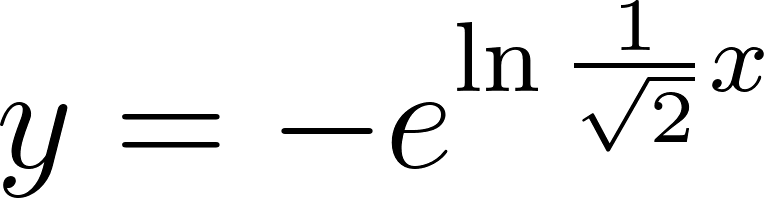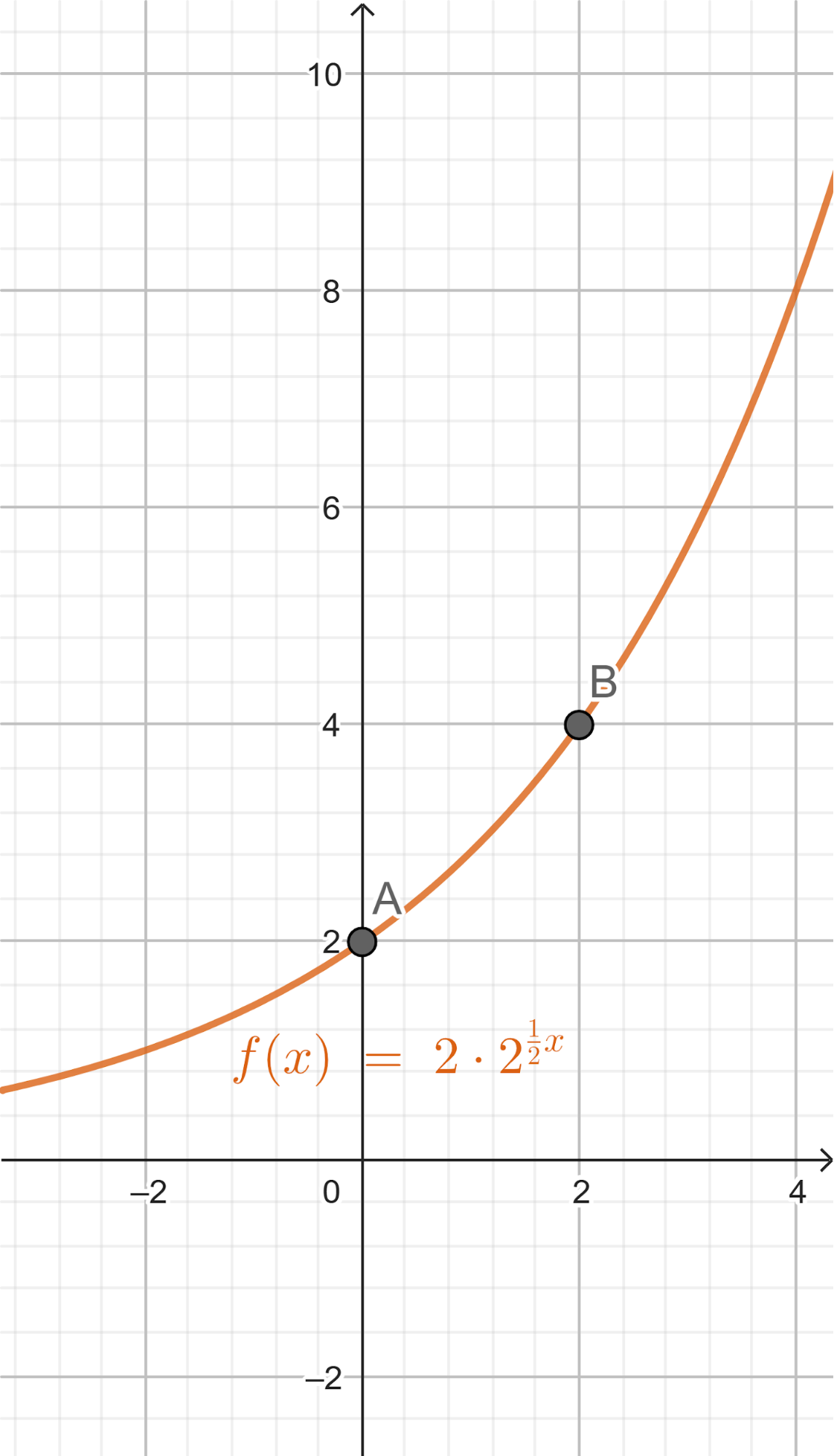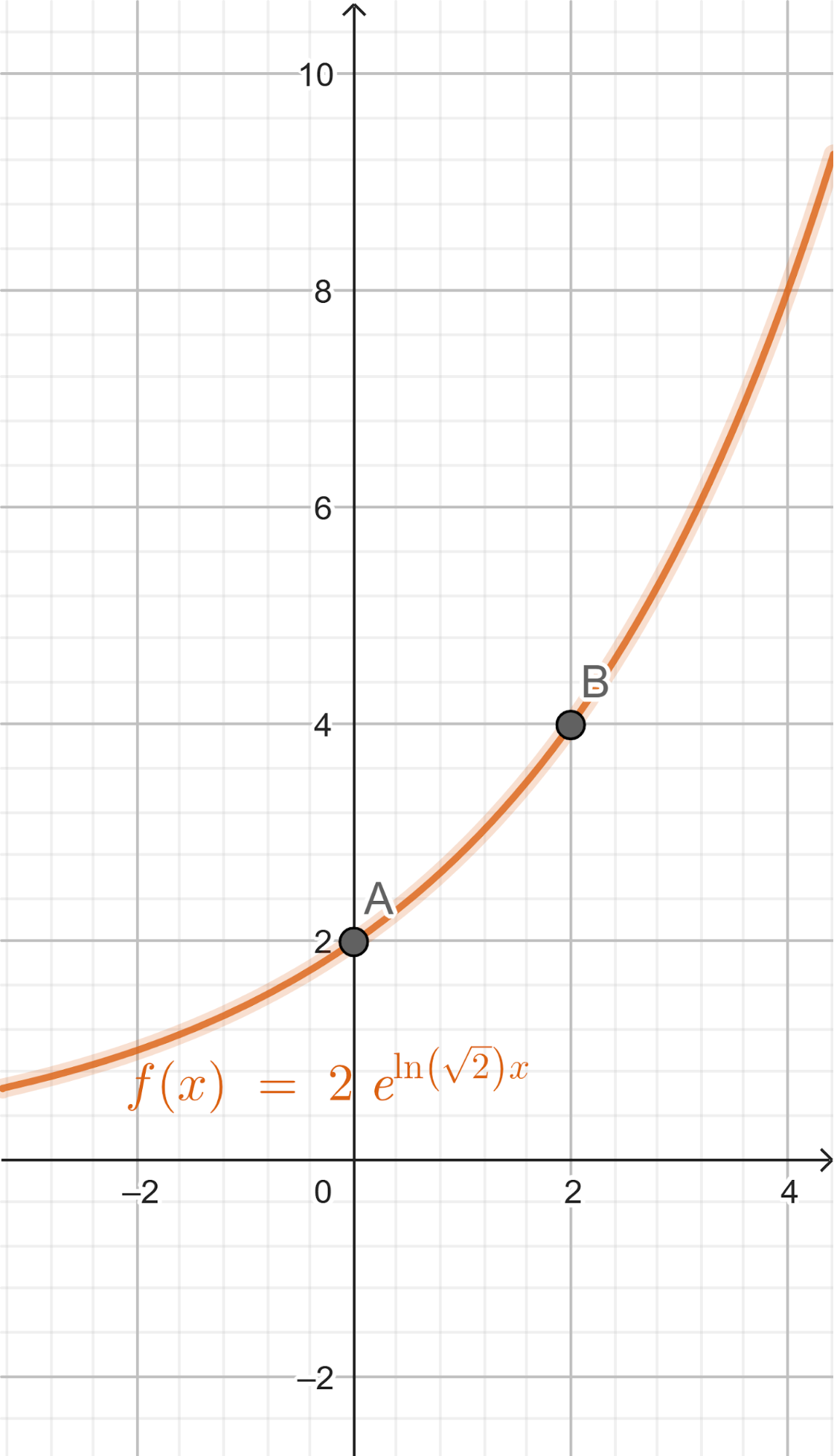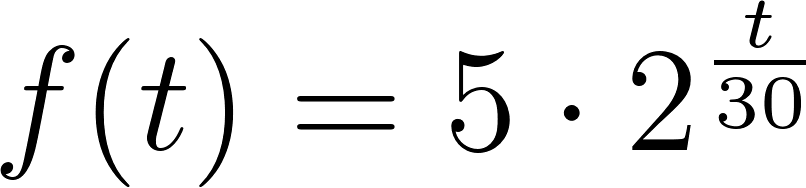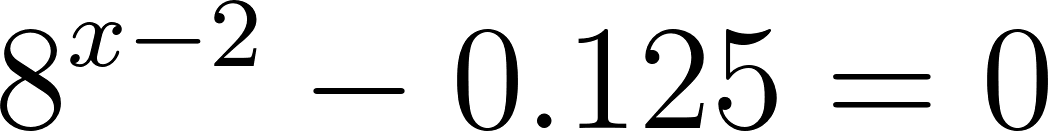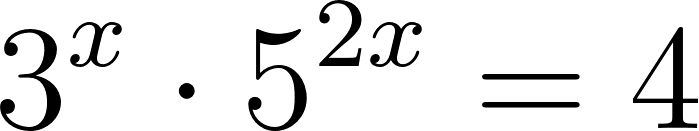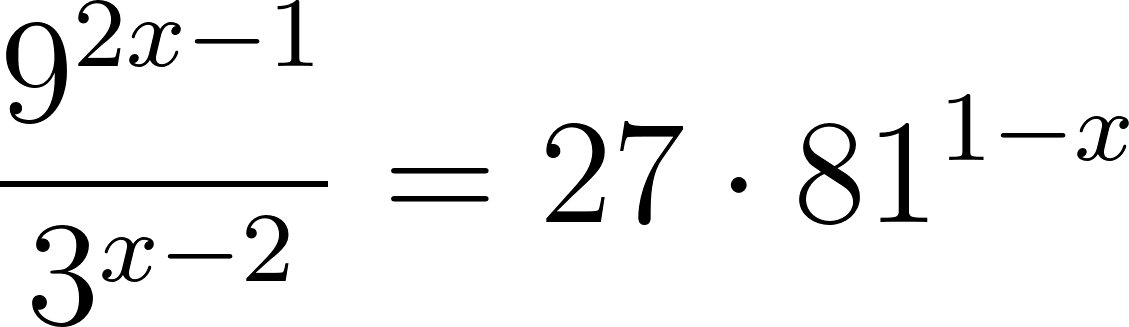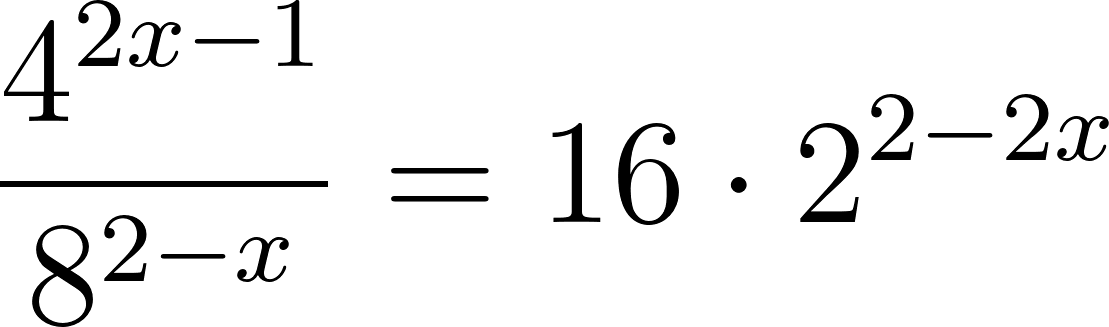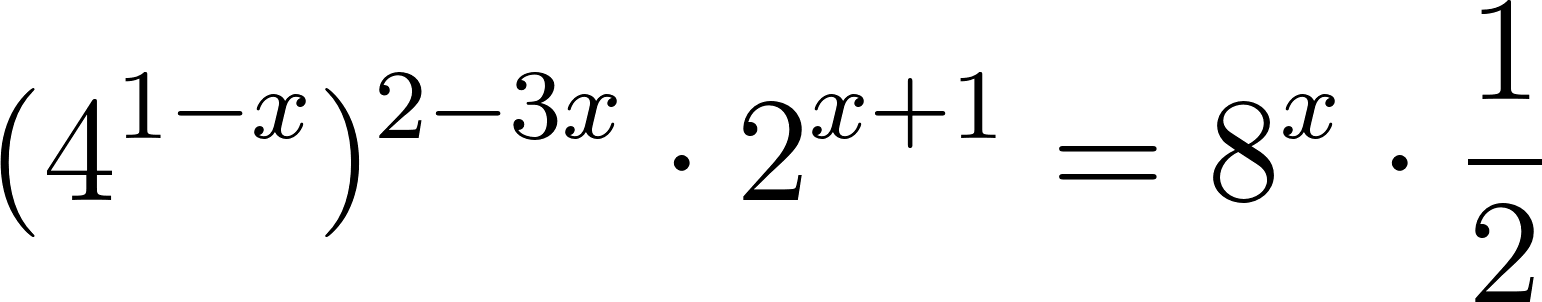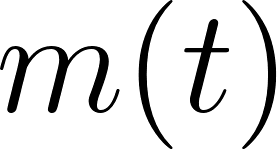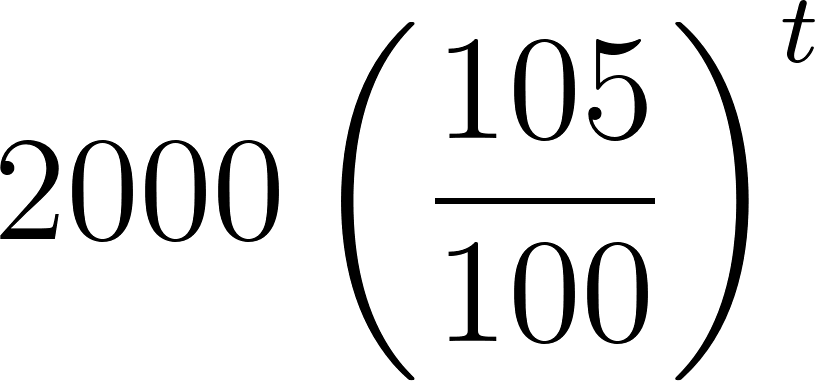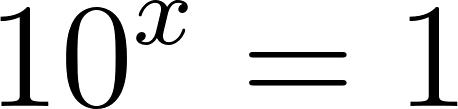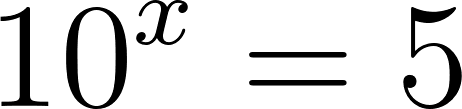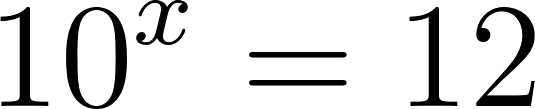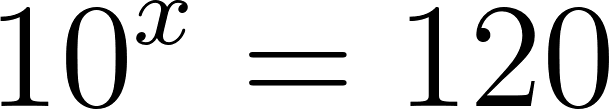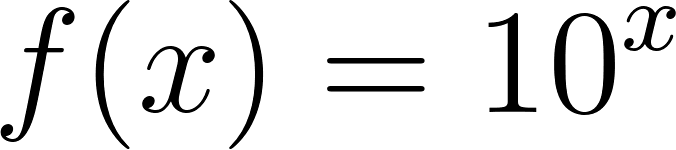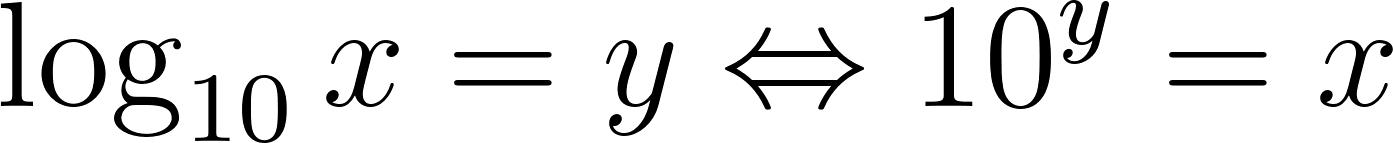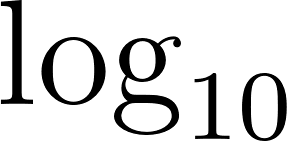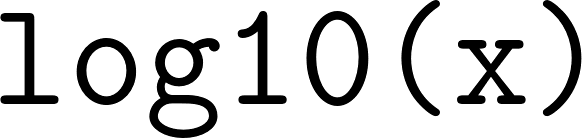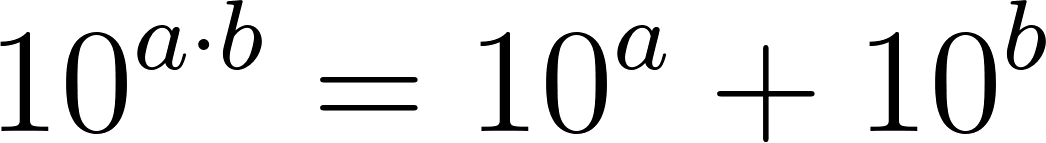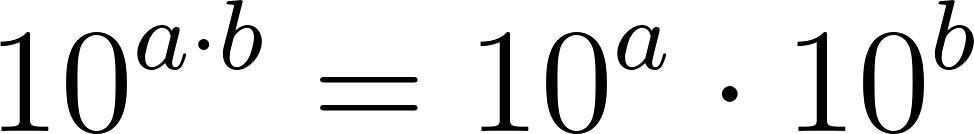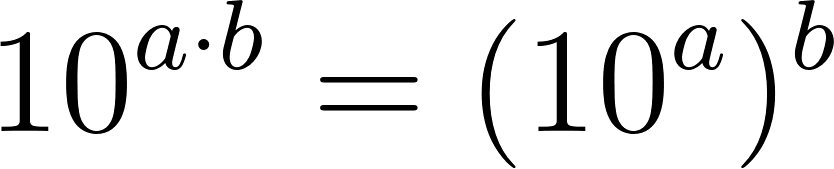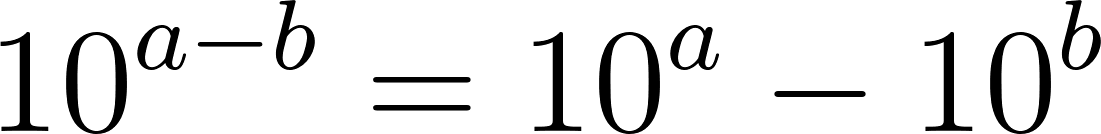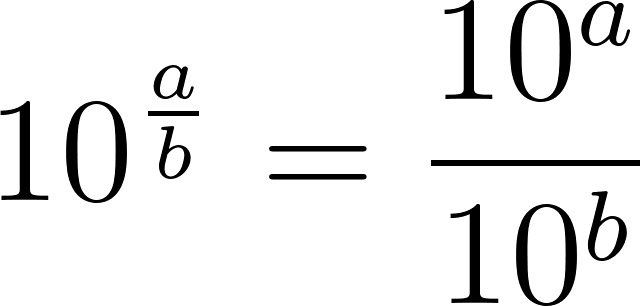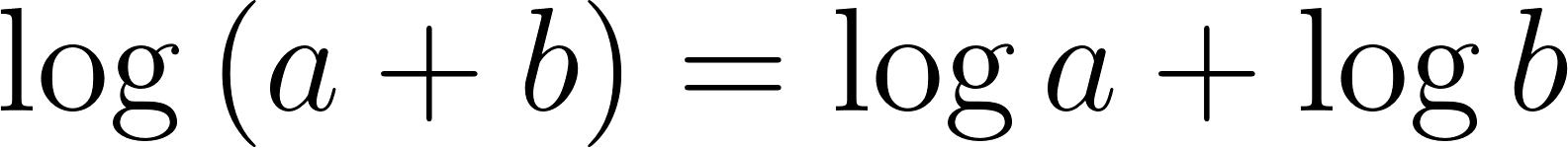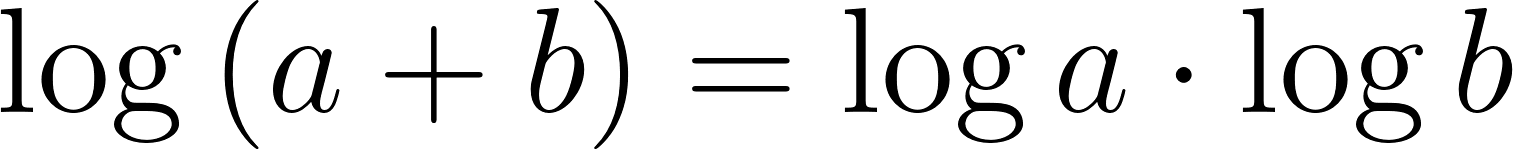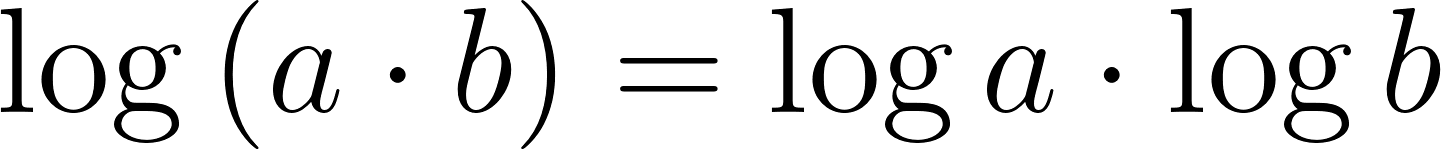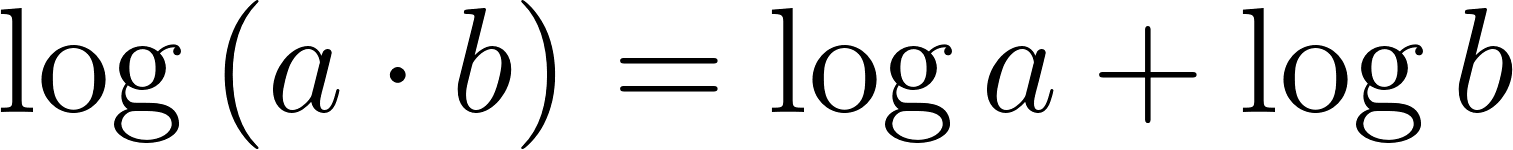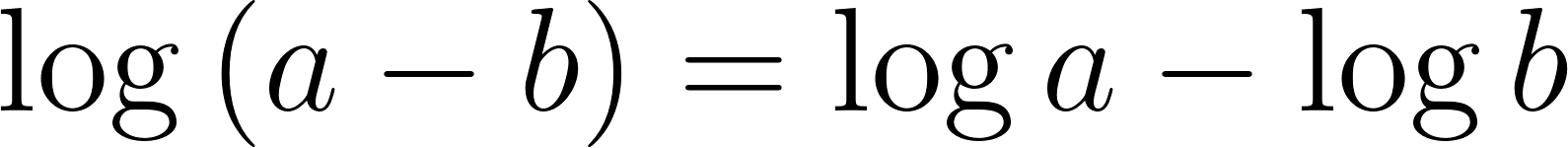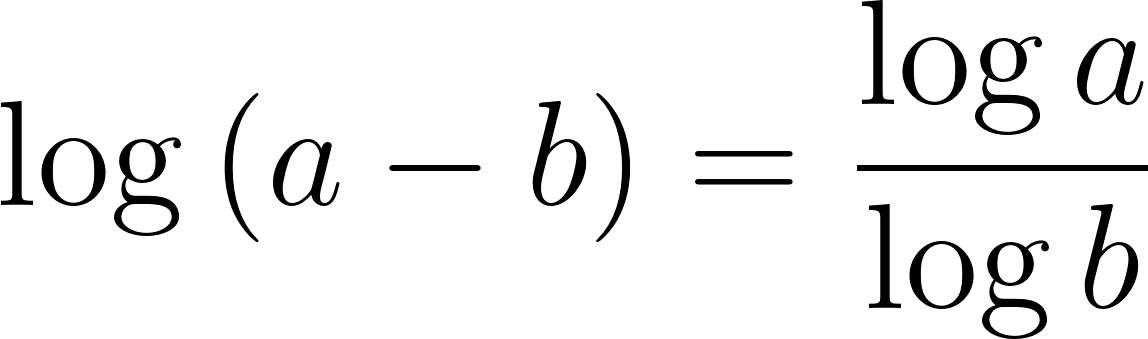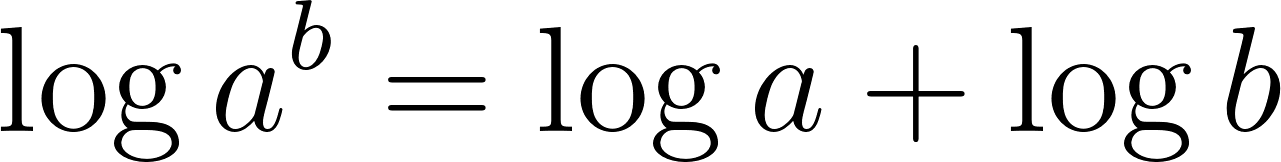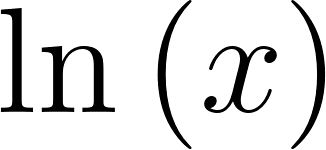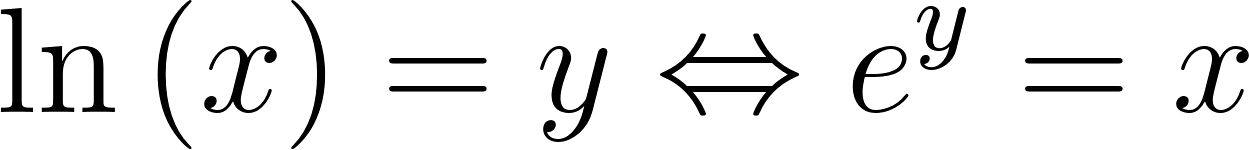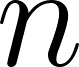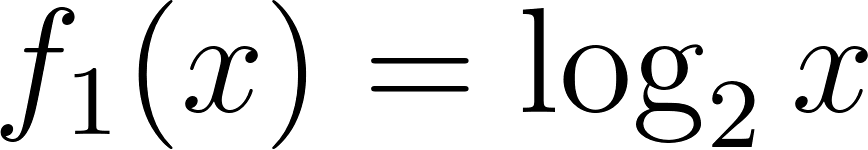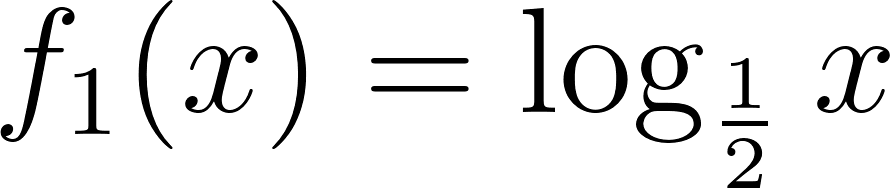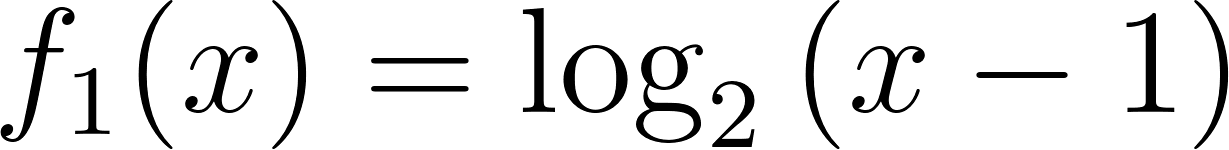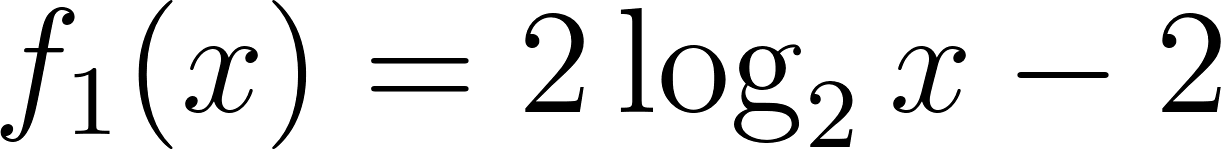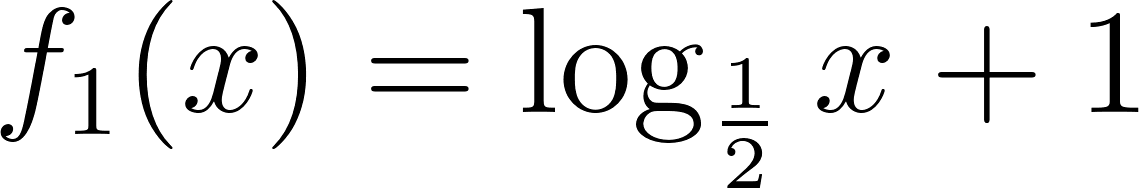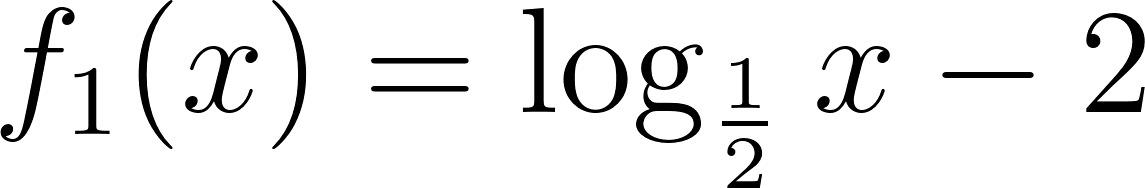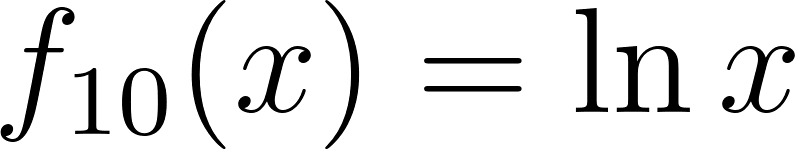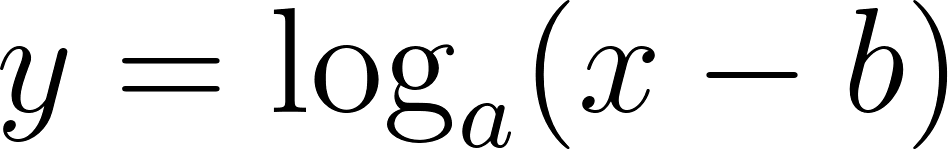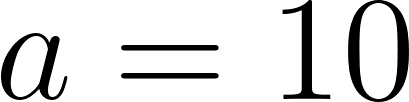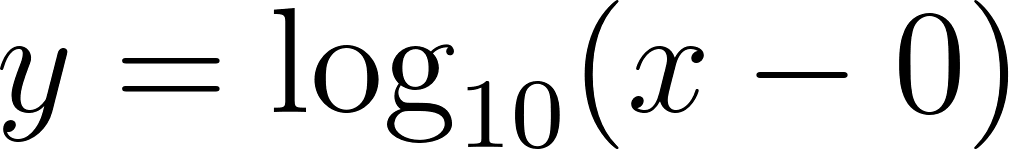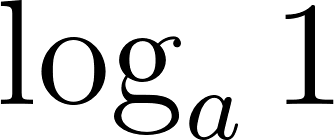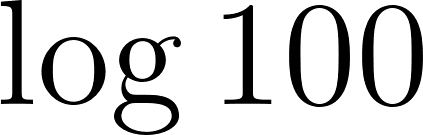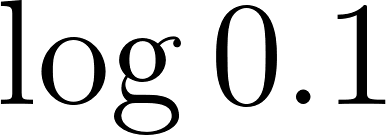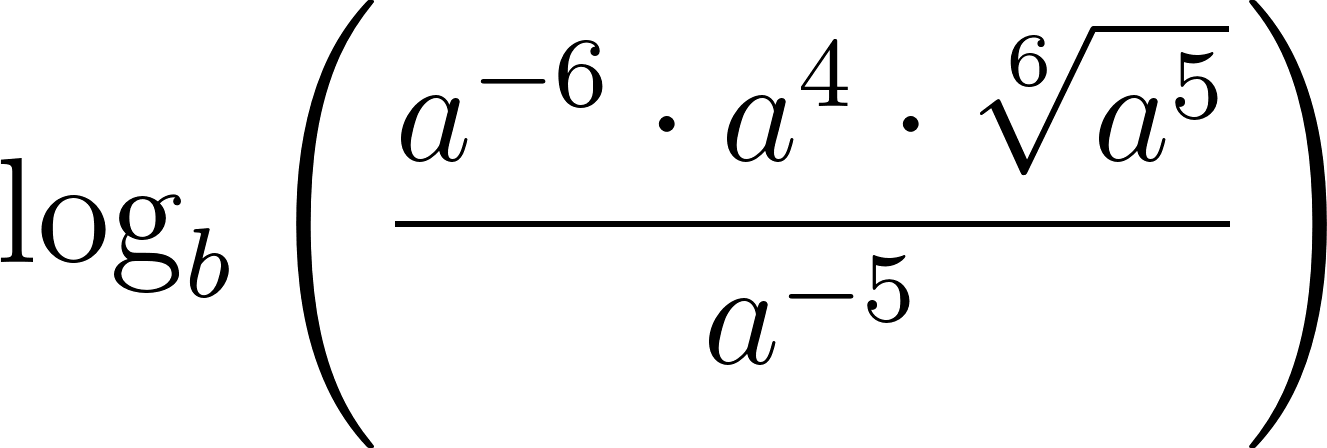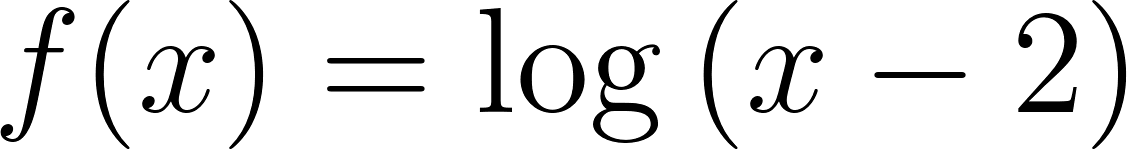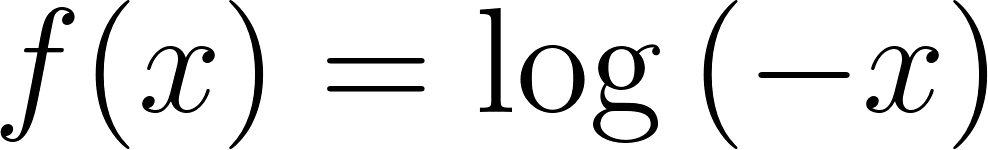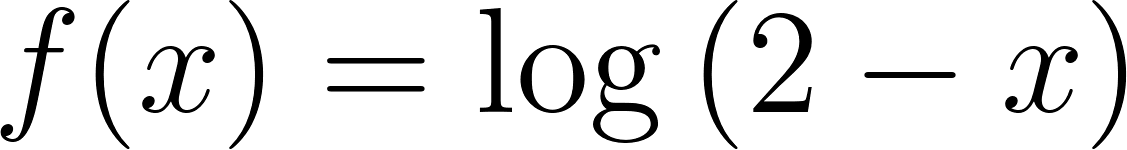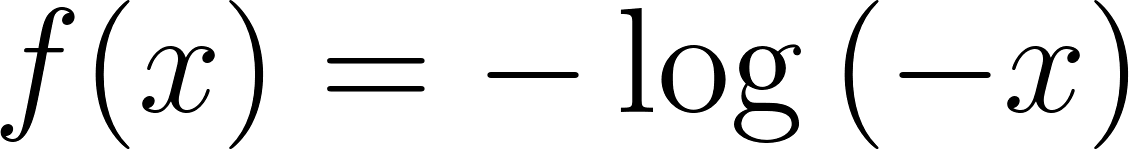Funciones Exponenciales y Logarítmicas
Envejecer, desintegrarse, sanar.
Objetivos de esta unidad
|
Teoría
- Video Similar al Problema 1: Modelos exponenciales
- Para relacionar fórmulas con gráficos: Problemas 5, 6 y 7.
- Para manejar la fórmula de una función exponencial: Problemas 12, 13, 14, 20 y 21.
- Para interpretar un modelo exponencial: Problemas 2, 16, 22 y 23.
- Para resolver ecuaciones exponenciales: Problema 17.
- Para crear un modelo exponencial: Problemas 9, 15 y 18.
- Dos apuntes con explicaciones y ejemplos para comprender mejor estos modelos:
- En este primer APUNTE EXPONENCIALES 1 se resuelve un problema de modelos exponenciales y también se explica cómo despejar una ecuación exponencial.
- En este segundo APUNTE EXPONENCIALES 2 se resuelven dos ejemplos básicos que explican cómo hallar la función exponencial conociendo dos puntos de su gráfica.
- En este video se resuelven dos problemas, donde se pide encontrar la fórmula de la función exponencial conociendo algunos datos de su gráfica.
- En este video se resuelve el Problema 9 de la guía.
Práctica
Problema 1 Crecimiento poblacional. Un pueblo tiene actualmente 2000 habitantes y su población está creciendo a razón de 5% por año.
- Estimen cuál será la población dentro de 10 años a partir de ahora.
Solución:
Año(t) | Población | Población | Población |
0 | 2000 | 2000 | |
1 | 2100 | ||
2 | 2205 | ||
3 | 2315.25 | ||
4 | 2431.0125 | ||
5 | 2552.563125 | ||
6 | 2680.191281 | ||
7 | 2814.200845 | ||
8 | 2954.910888 | ||
9 | 3102.656432 | ||
10 | 3257.789254 |
- Estimen cuánto tardará la población en duplicarse, si continúa siempre creciendo a este ritmo.
Solución:
Averiguamos para que dé 4000.
Para despejar aplicamos la inversa de la exponencial que es el logaritmo y para poder calcular el logaritmo en base distinta de 10, debemos realizar la división entre el número del lado de la igualdad y la base del exponente, es decir:
Entonces:
La población tardará en duplicarse aproximadamente 14 años.
- Escriban una fórmula para la población P como función del tiempo t en años.
Solución:
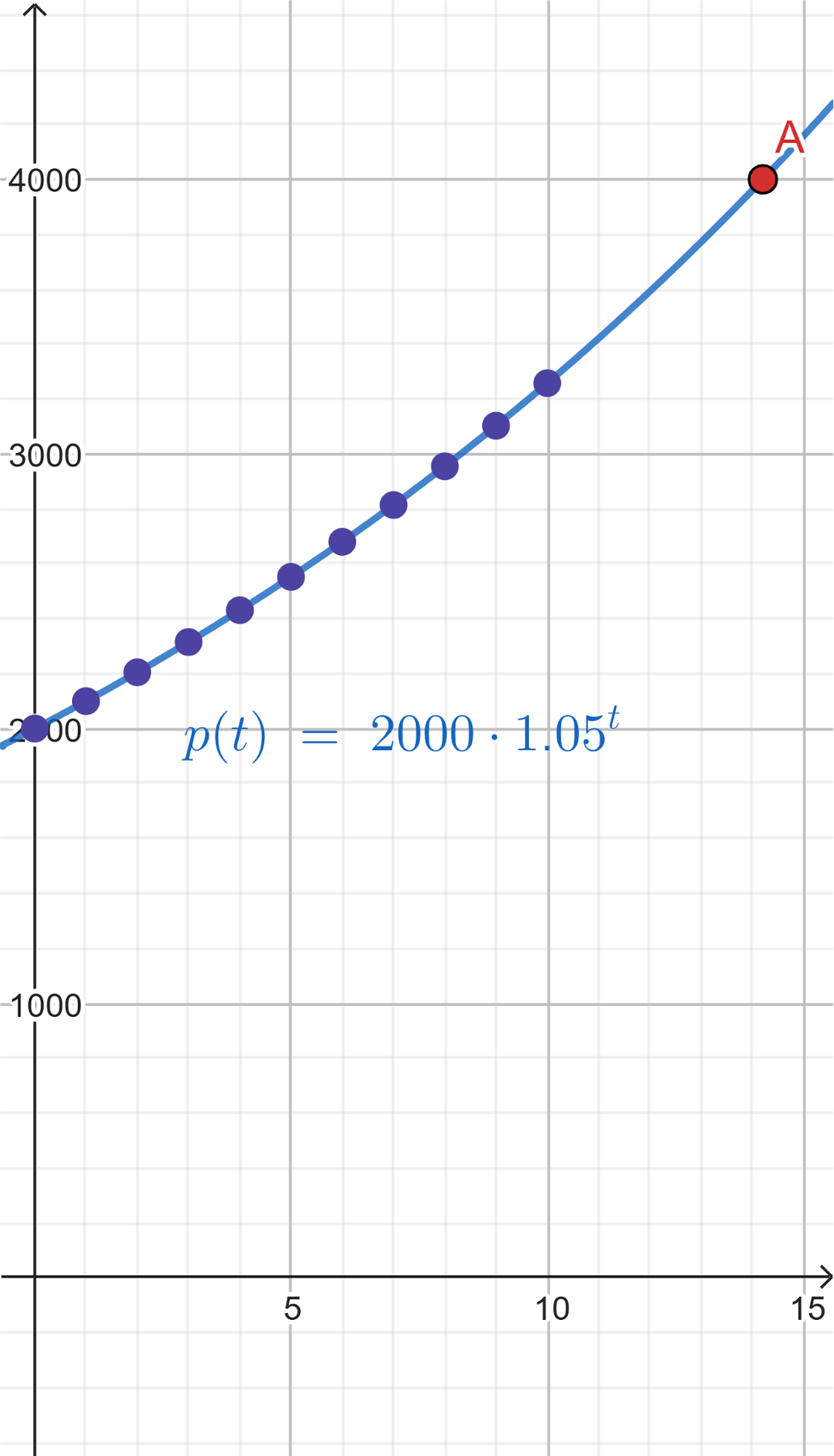
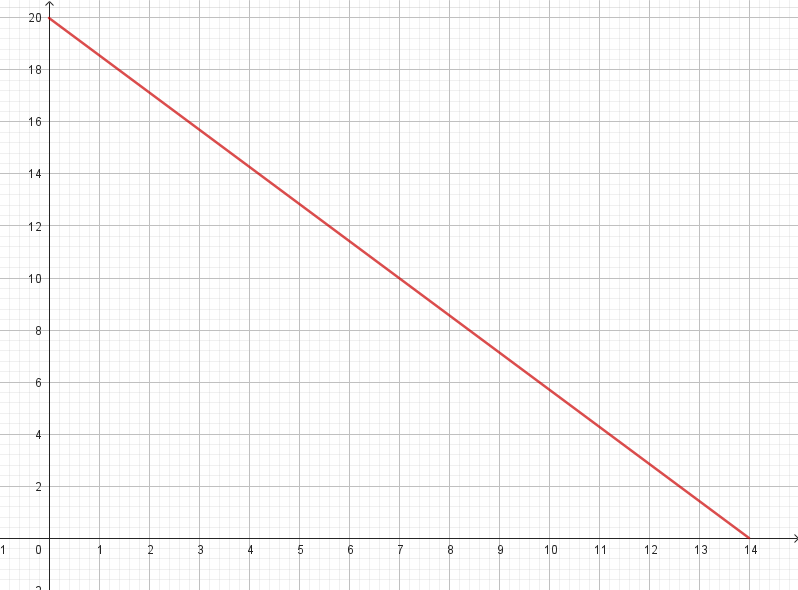
- Tracen una gráfica de P en función de t.
Solución:
- Revisen sus estimaciones en las preguntas a y b.
Solución:
Coinciden con lo planteado.
- ¿Cómo se modificaría la fórmula si la población crece de la misma manera, pero el tiempo se mide en meses?.
Solución:
Con en meses.
Año(t)=Mes(t) | Población | Población | Población |
0 | 2000 | ||
1=12 | 2100 | ||
2=24 | 2205 | ||
3=36 | 2315.25 | ||
4=48 | 2431.0125 | ||
5=60 | 2552.563125 | ||
6=72 | 2680.191281 | ||
7=84 | 2814.200845 | ||
8=96 | 2954.910888 | ||
9=108 | 3102.656432 | ||
10=120 | 3257.789254 |
Problema 2 Mezclas y concentraciones. Un barril de 200 L se llena por completo con agua pura. A continuación se bombea hacia el barril agua salada con una concentración de y la mezcla resultante sale a la misma tasa. La cantidad de sal en el barril en el tiempo t se determina mediante:
donde t se mide en minutos y se mide en gramos.
- ¿Cuánta sal está en el barril después de 5 min?.
Solución:
Con calculadora.
- ¿Cuánta sal está en el barril después de 10 min?.
Solución:
Con calculadora
- Discutan acerca de si son verdaderas o falsas las siguientes afirmaciones:
- A medida que transcurra el tiempo siempre habrá cada vez más sal en el barril.
- Como cada vez habrá más sal en el barril, en algún momento habrá 10000 g de sal.
Solución:
Si uno evalúa en un mayor tiempo puede parecer que cada vez habrá más sal, pero está limitada a acercarse a 8000 gramos por litro. por lo tanto jamás habrá 10000 g de sal sin importar el tiempo transcurrido.
Evaluamos:
- :
Ya la calculadora da 8000 por deficiencia de hardware.
- Dibujen una gráfica de la función
Solución:
- Usen la gráfica del inciso anterior para volver a pensar las respuestas dadas en el ítem c.
Solución:
Se confirman las respuestas dadas.
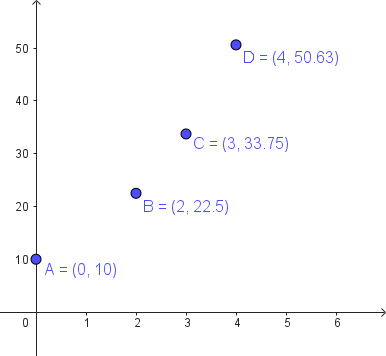
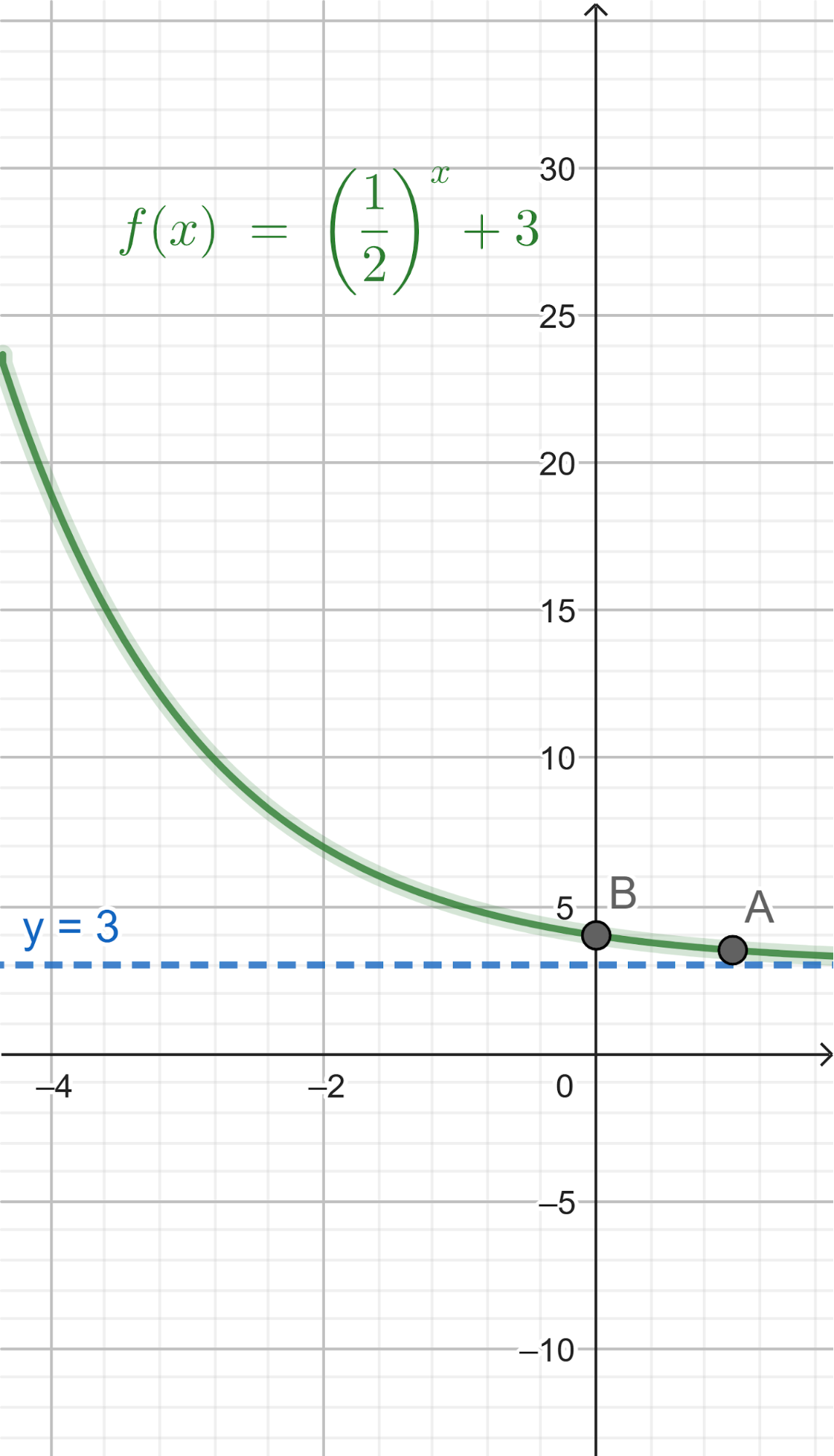
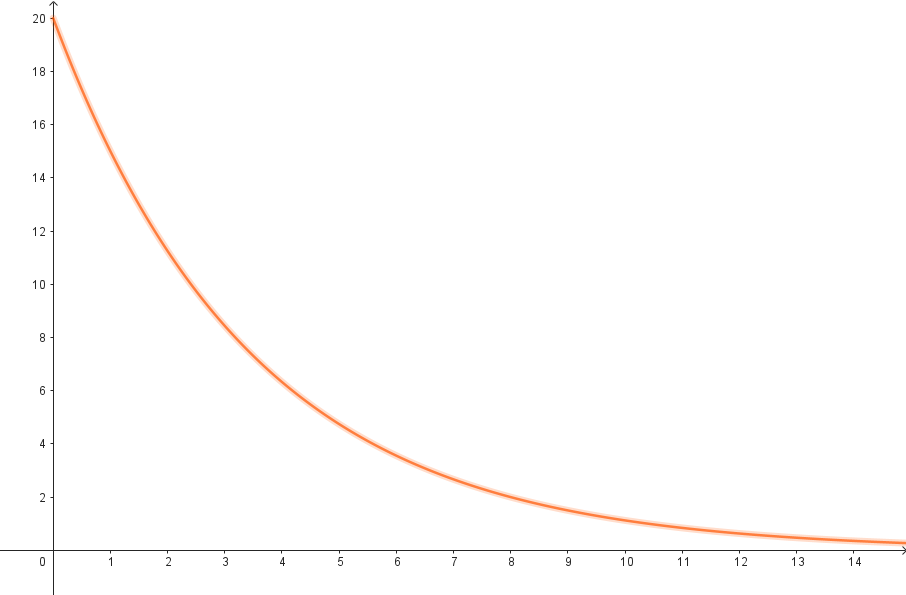
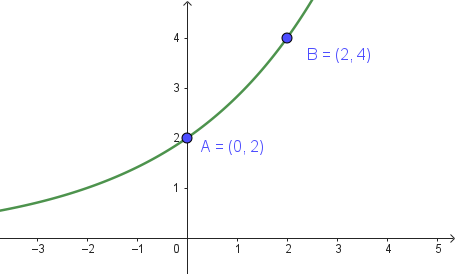
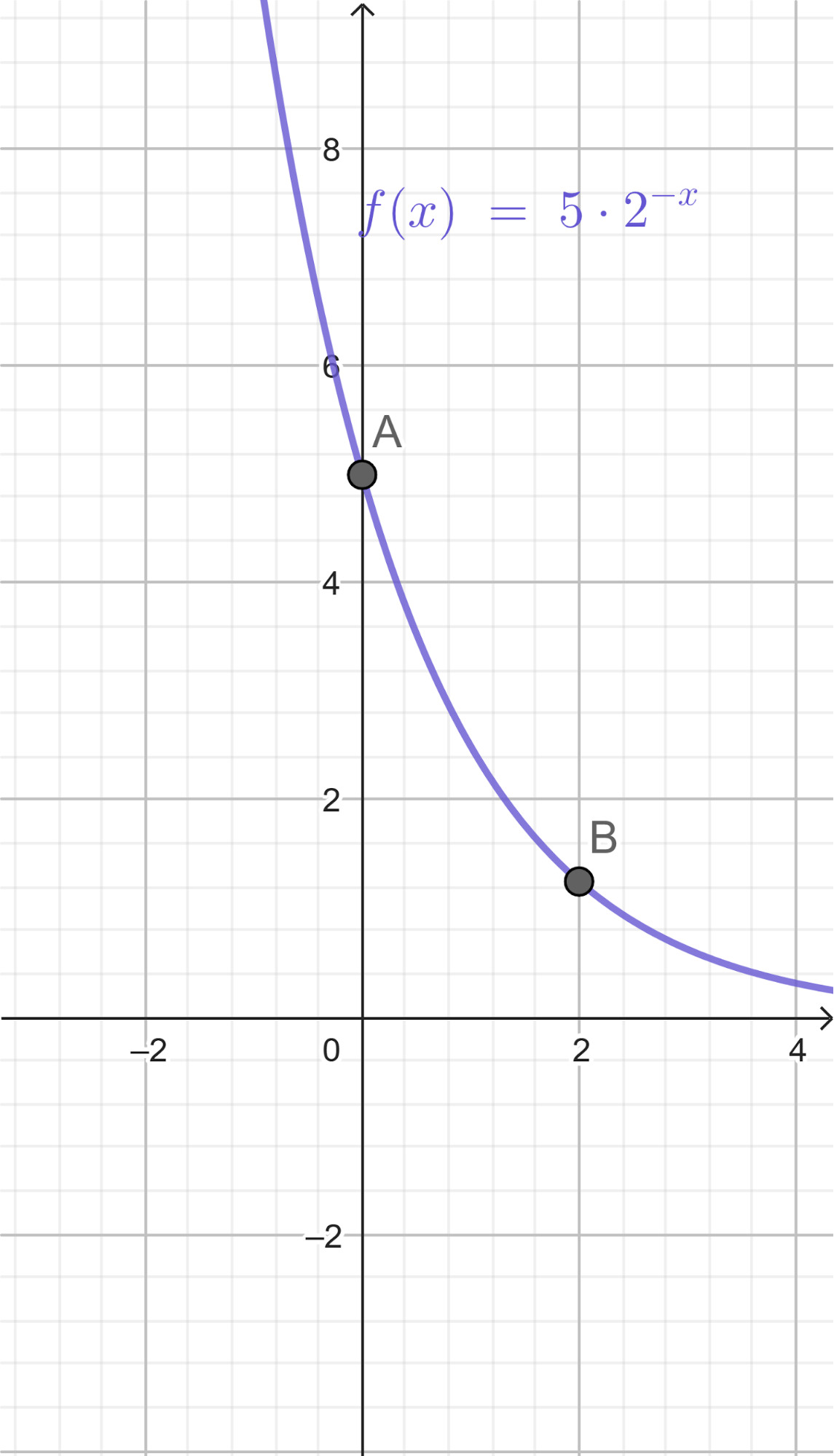
Problema 3 La figura muestra algunos puntos del gráfico de una función exponencial .
- Estimen, mirando el gráfico, el valor de .
Solución:
El valor se encontrará entre 22.5 y 33.75 ya que son los valores de 2 y 3.
- Escriban la fórmula de una función que se corresponda con el gráfico.
Solución:
Usamos dos puntos de la gráfica para hallar la función:
Verificamos:
- Calculen y comparen con el punto a.
Solución:
Confirmando nuestra estimación.
Problema 4 Lean el siguiente cuadro:
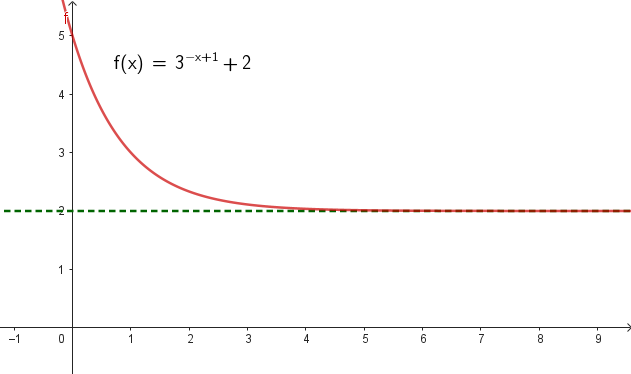
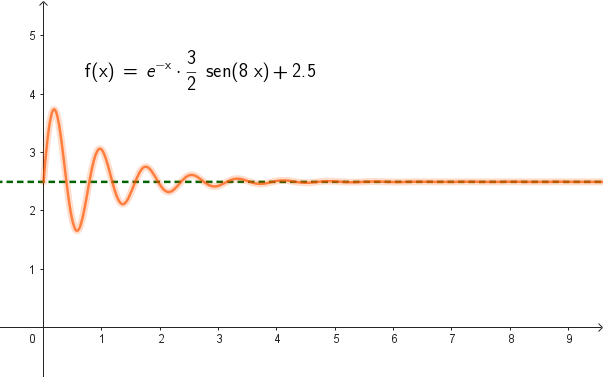
Una asíntota horizontal de una función es una recta horizontal a la que el gráfico de se va acercando hasta confundirse con ella. Interpretación gráfica: Los siguientes gráficos muestran ejemplos de distintas funciones y sus asíntotas horizontales. | ||
Interpretación en el contexto de este problema: Que el gráfico de se vaya confundiendo con la recta de ecuación a medida que crece t significa que cuanto más tiempo pase, más cerca estará el barril de estar completamente lleno con el agua que estaba ingresando y, por lo tanto, la cantidad de sal se acercará a la que hay en 200 L de agua con de sal. Definición formal: La recta de ecuación es una asíntota horizontal de una función , si la diferencia se puede hacer tan cercana a 0 como se quiera, desde cierto valor de t en adelante. En tal caso decimos que tiende a cuando tiende a . Y lo escribimos de esta manera: Si se desea precisar que la asíntota corresponde a las crecientes o a las decrecientes se escribe, respectivamente: o |
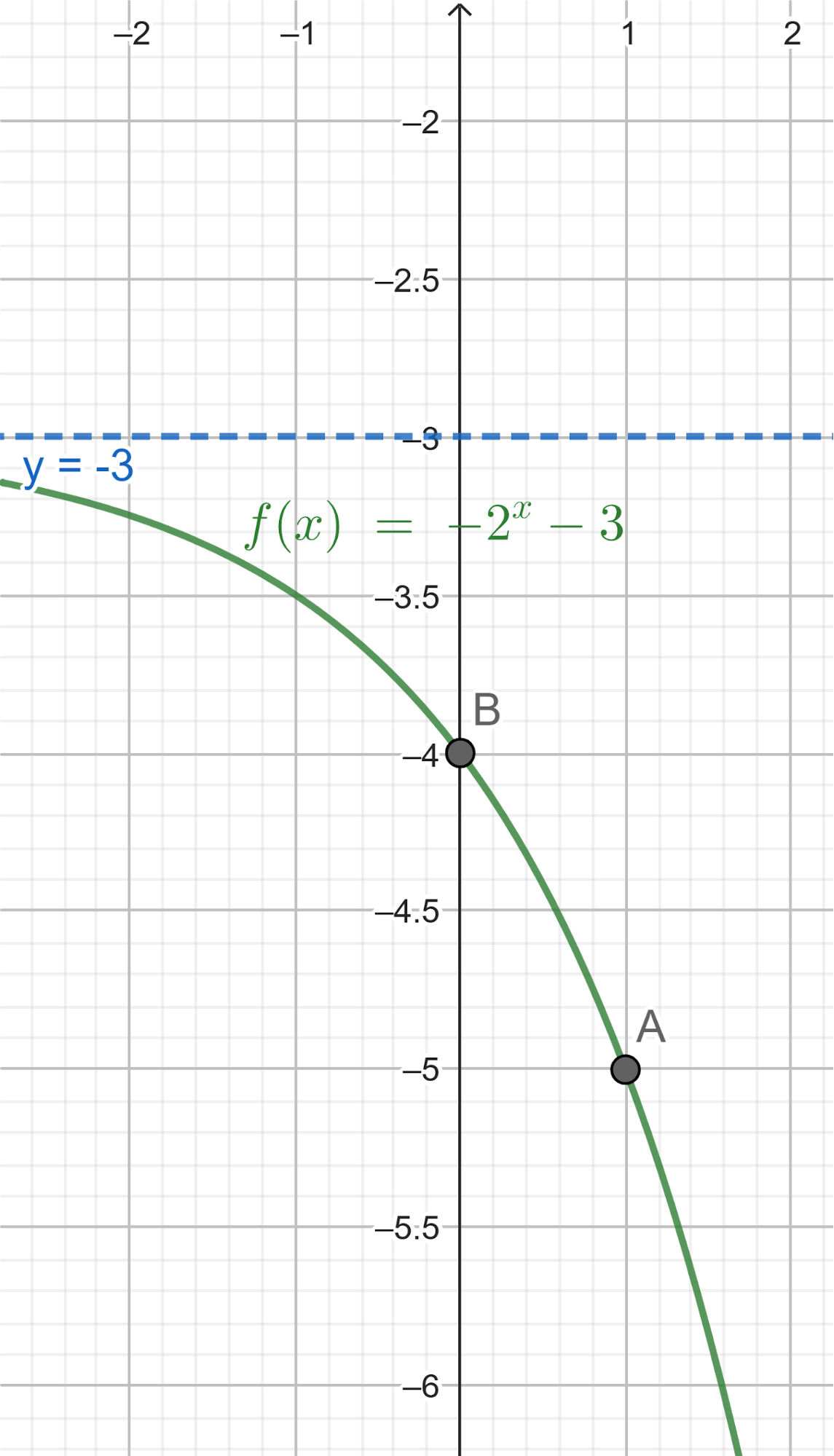
Construyan en GeoGebra tres deslizadores a, b, c y definan la función (Que se escribe f(x)=c+a b^x ). Investiguen cómo influyen los valores de los deslizadores para que:
- La función tenga una asíntota del tipo o del tipo , donde puede ser positivo, negativo o cero.
- La función sea creciente (Describe un fenómeno donde la cantidad va en aumento, como en el Problema 1) o decreciente (Describe un fenómeno en el que la cantidad disminuye).
Escriban un pequeño informe en el que se consideren todos los posibles, acompañados de un gráfico ilustrativo, dibujado a mano. Elijan cómo les conviene organizar la información para que sea completa, ordenada y de fácil lectura. El objetivo de este informe es que sirva de guía para trazar un gráfico aproximado de una función exponencial, sin tener que construir una tabla de valores.
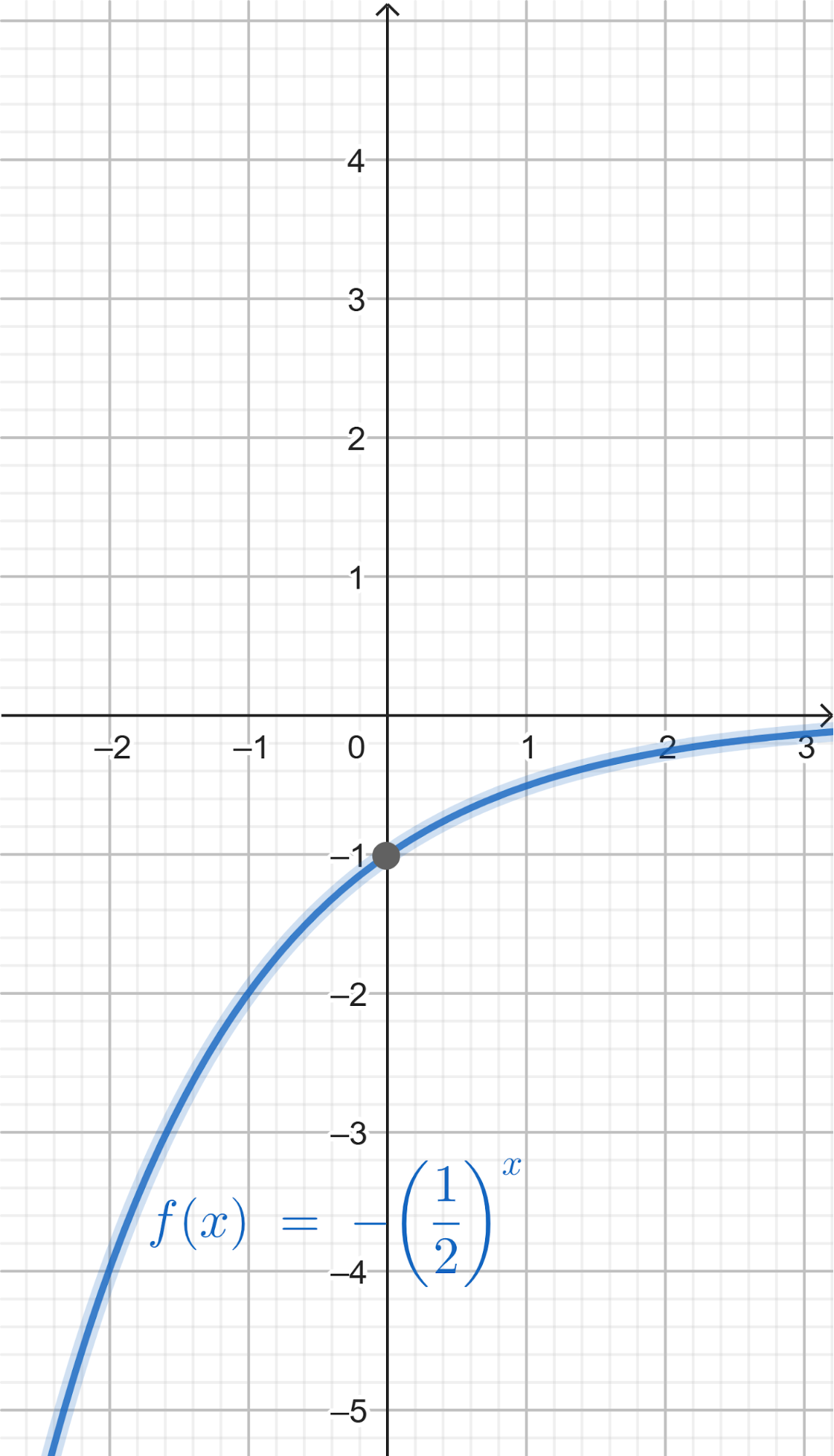
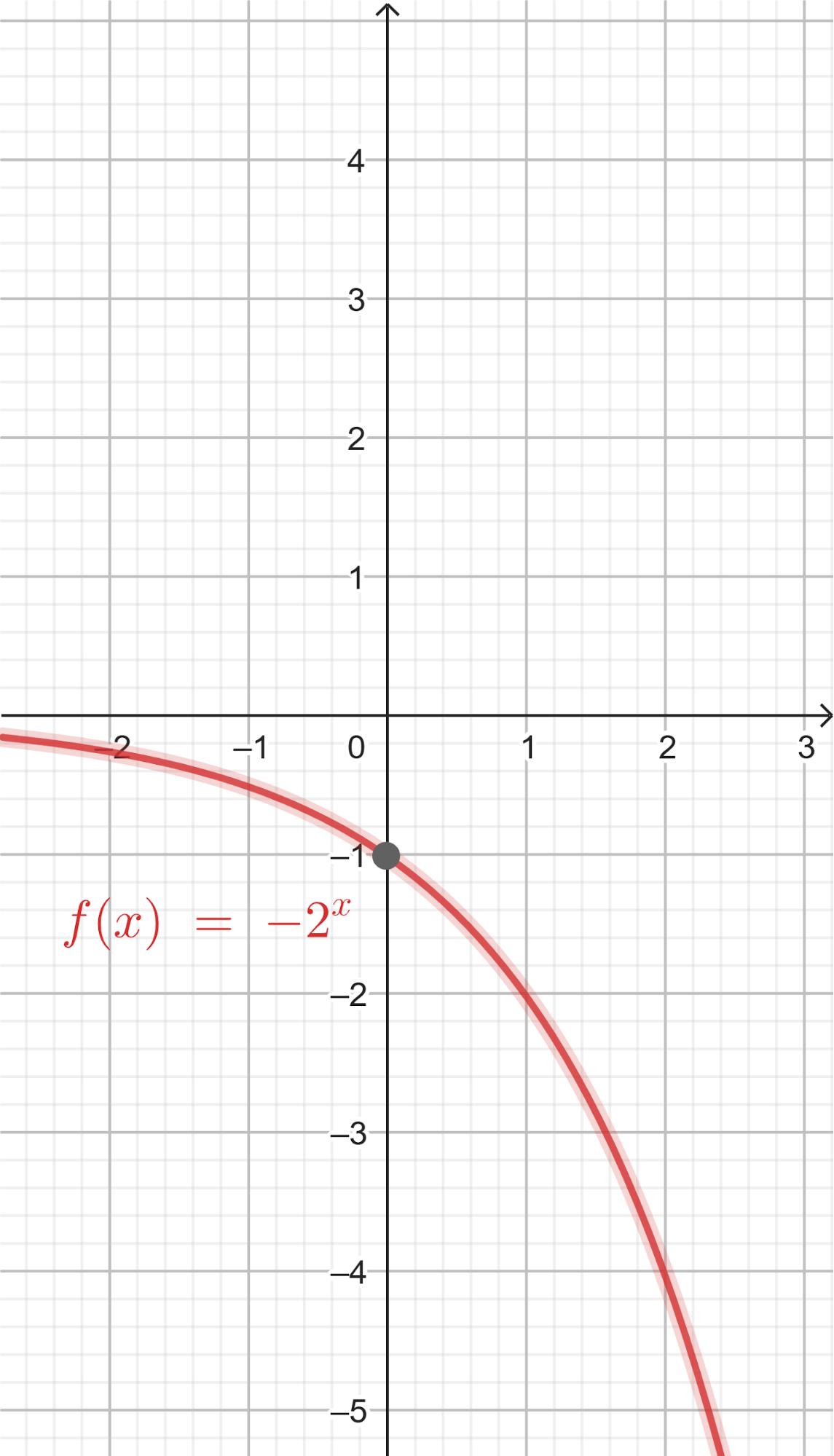
Problema 5 Dadas las siguientes funciones exponenciales:
Dom Im Intersección: Asíntota: Dom Im Intersección: Asíntota: Dom Im Intersección: Asíntota: Dom Im Intersección: Asíntota: | Dom Im Intersección: Asíntota: Dom Im Intersección: Asíntota: Dom Im Intersección: Asíntota: Dom Im Intersección: Asíntota: | Dom Im Intersección: Asíntota: Dom Im Intersección: Asíntota: Dom Im Intersección: Asíntota: Dom Im Intersección: Asíntota: |
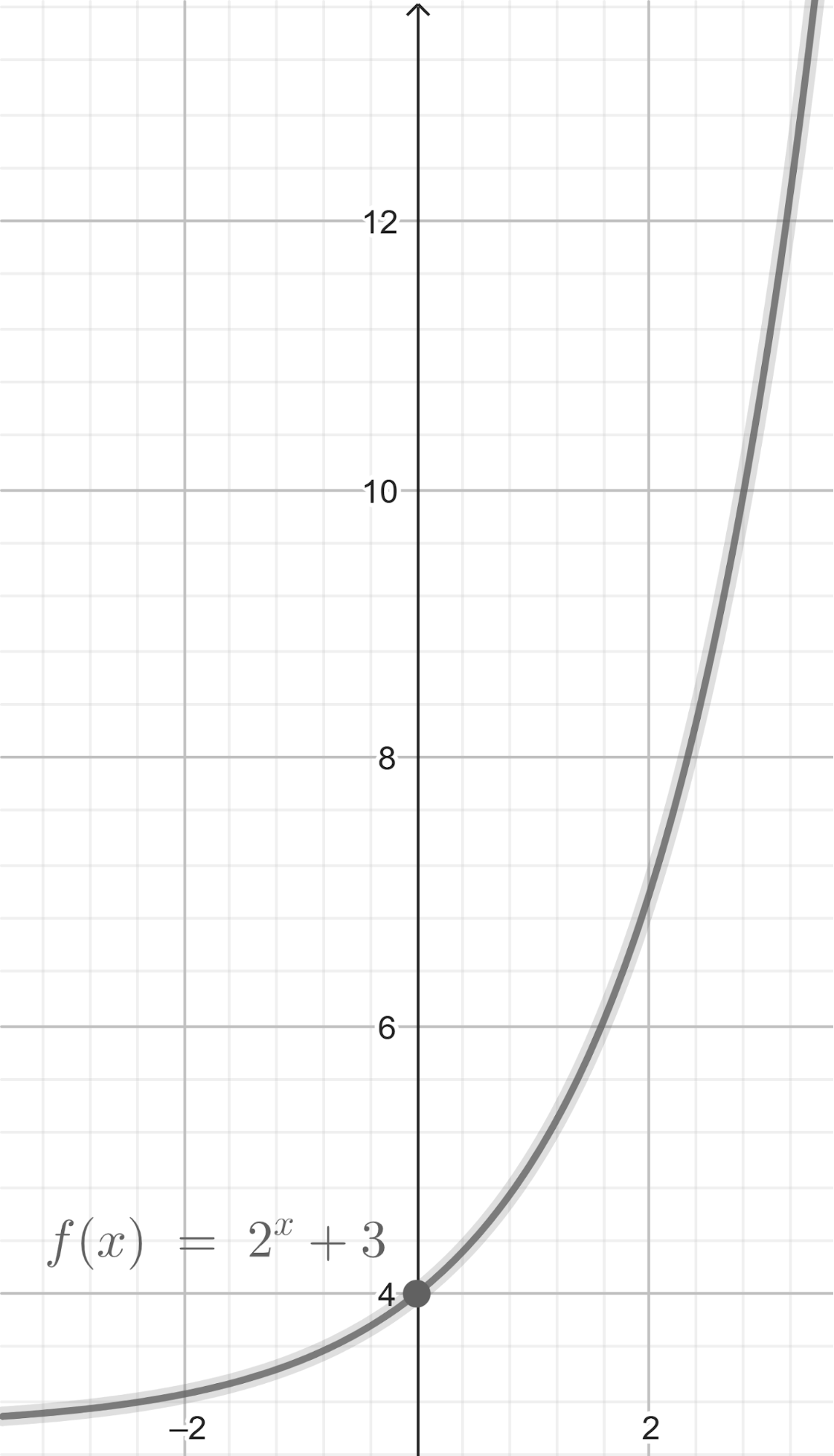
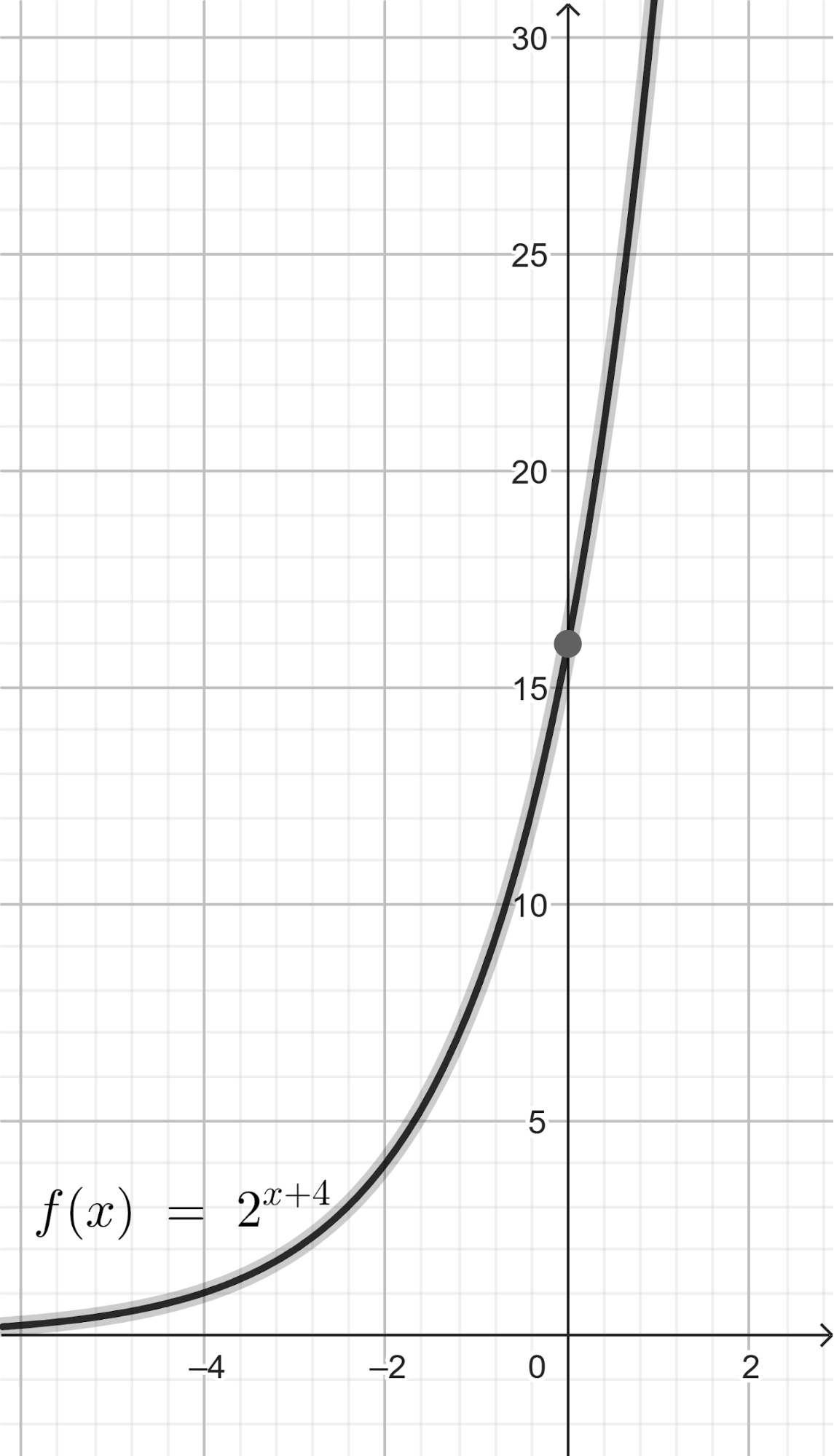
- Grafique cada una.
- Determine Dominio e Imagen.
- Halle, si posee, las intersecciones con los ejes.
- Indique si tiene asíntota y en tal caso de una ecuación de la misma.
Solución:
Para calcular la asíntota usamos el valor de término independiente. O calculamos el límite de x cuando tiende a infinito y menos infinito. Donde:
Si entonces
Si entonces
Cuando elevemos a b se convertirá en fracción
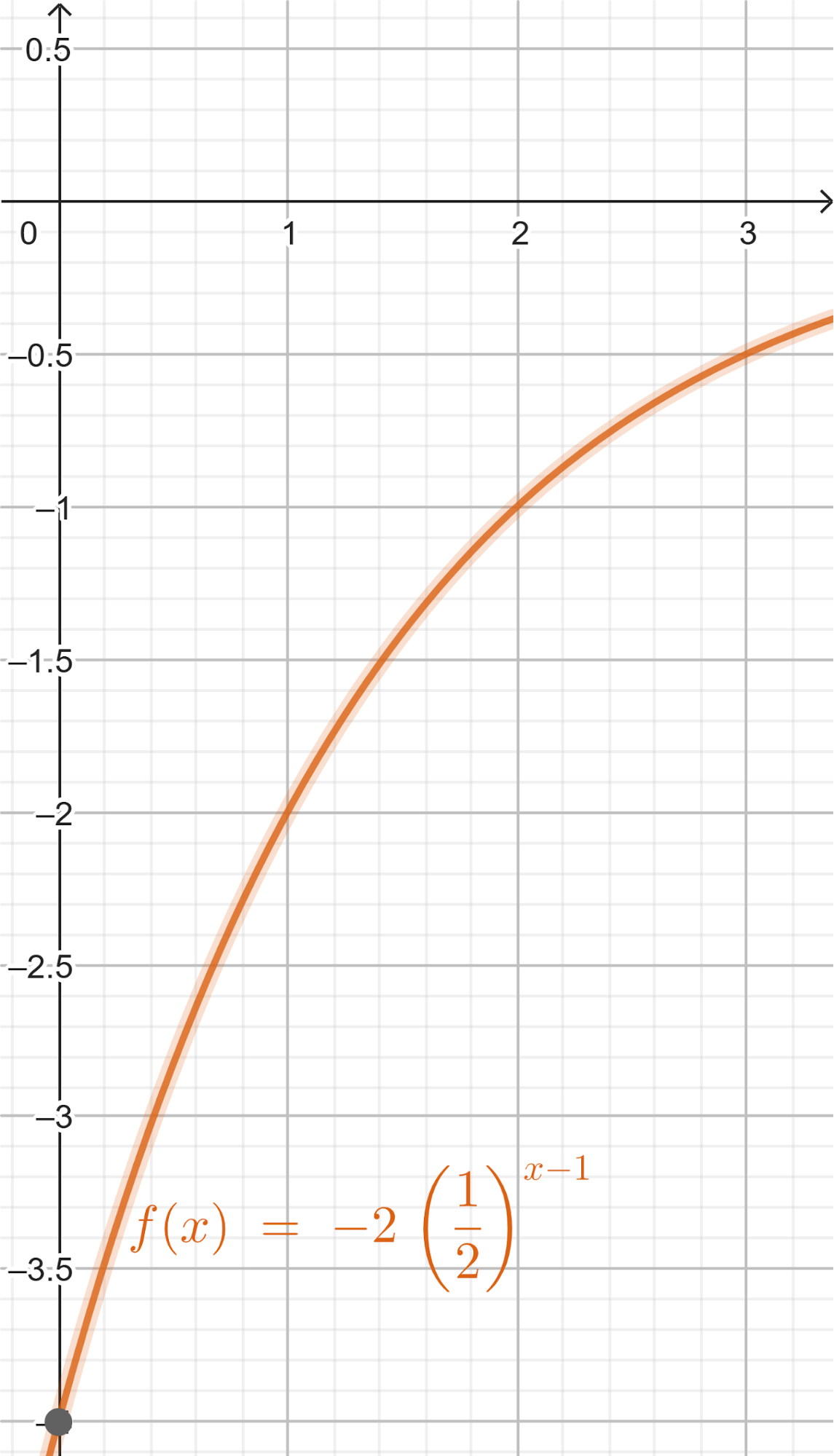
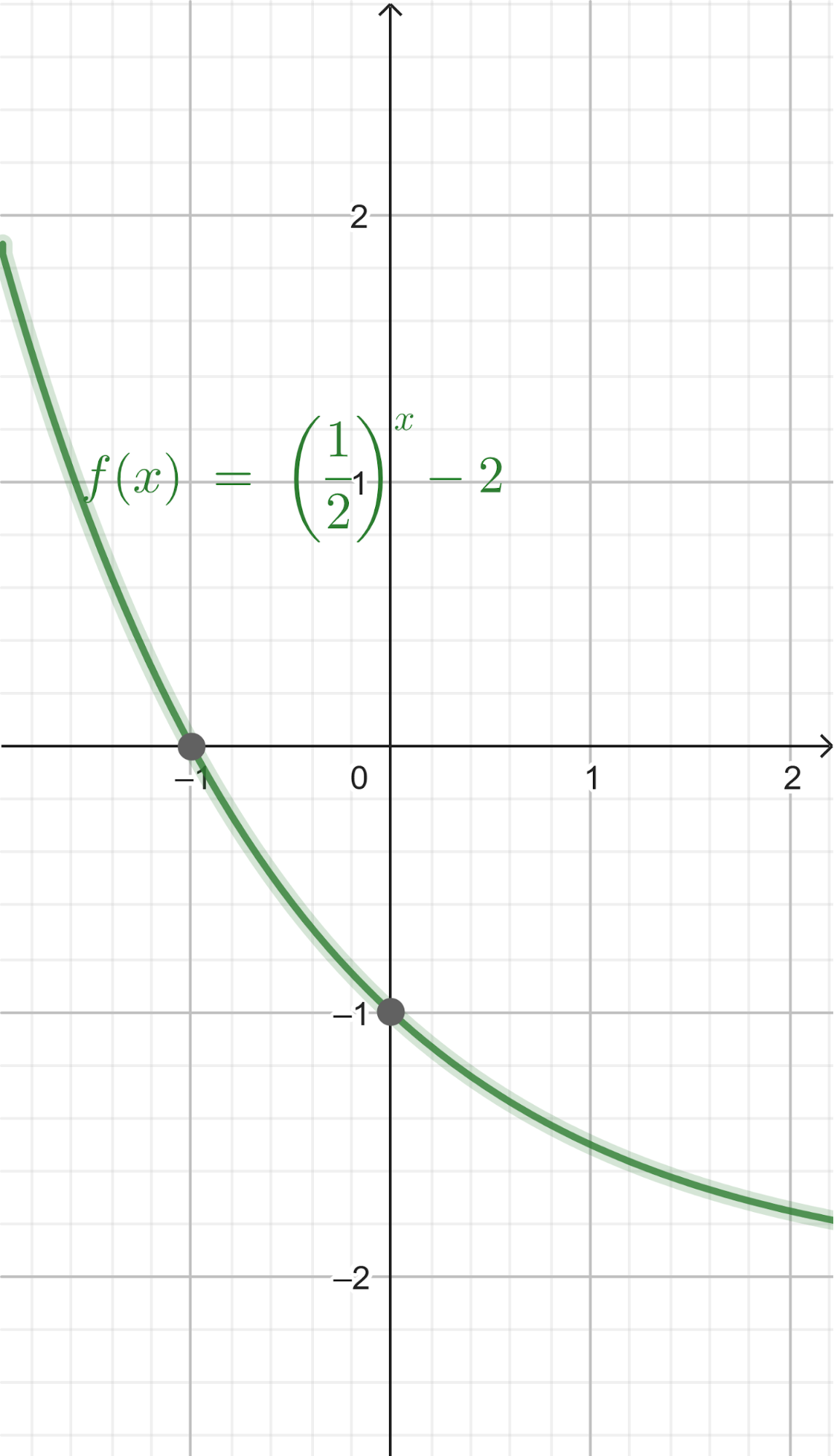
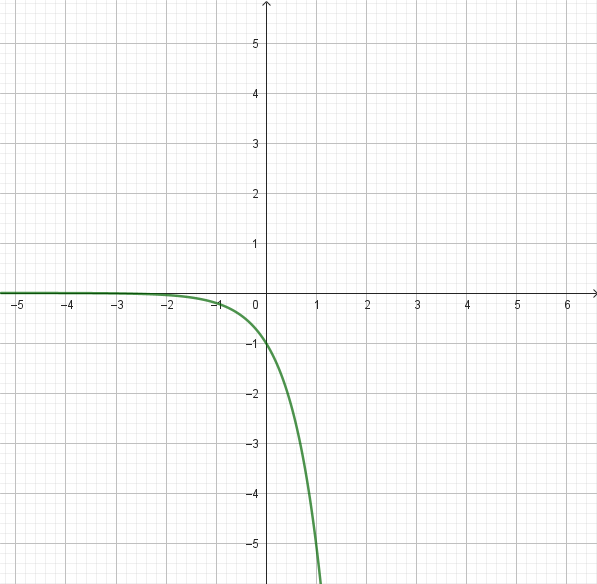
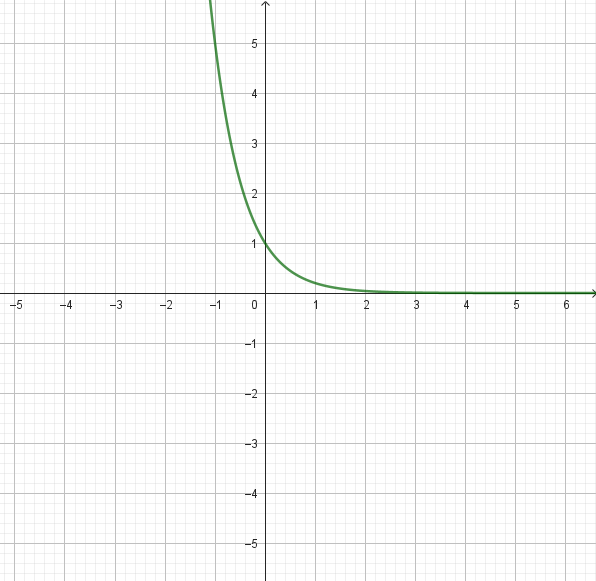
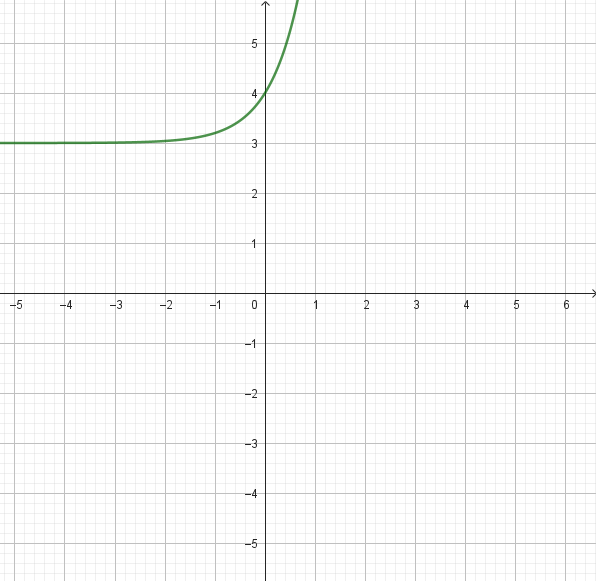
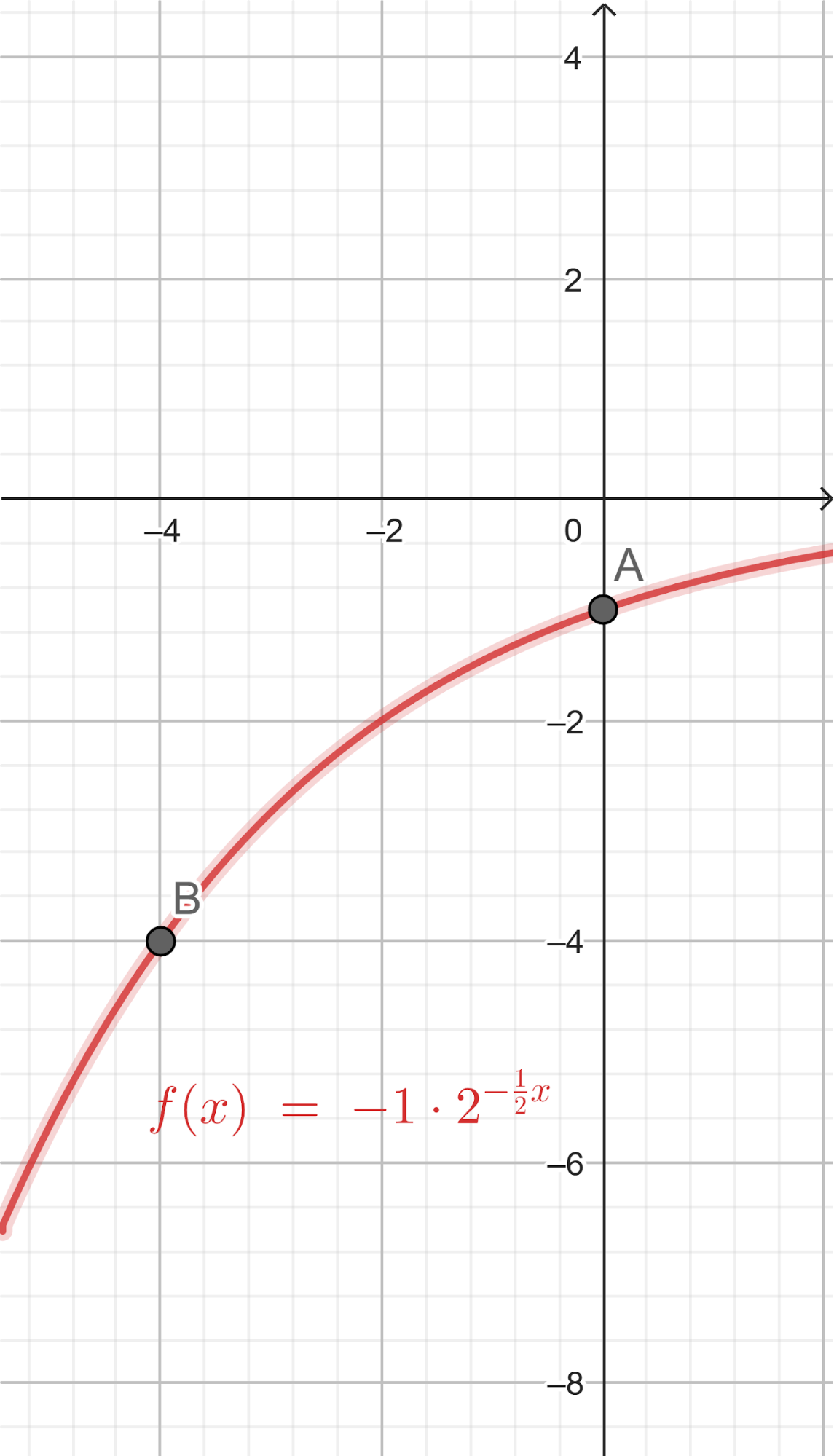
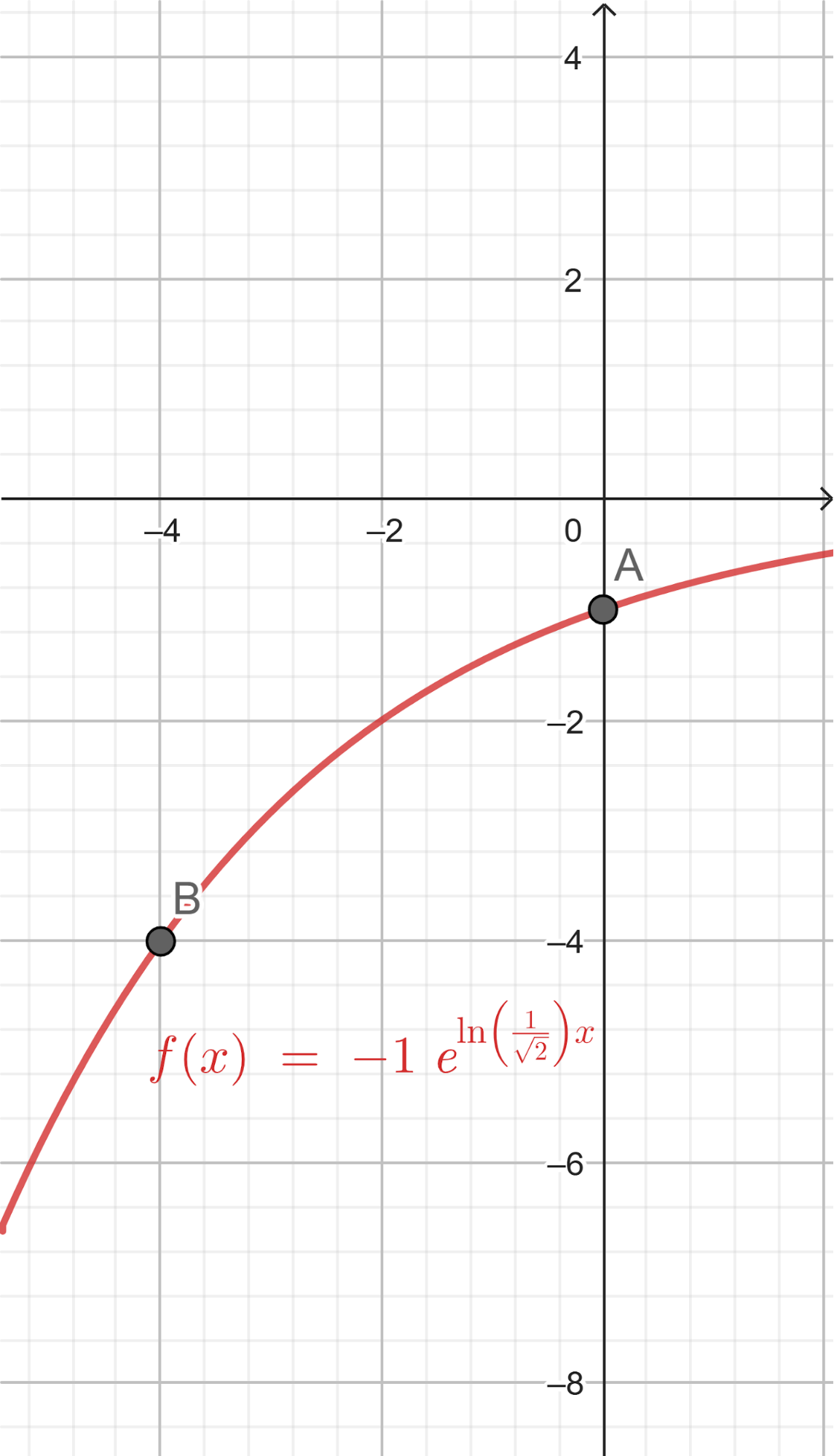
Problema 6 Decidan si cada gráfica corresponde a alguna de las siguientes funciones exponenciales, indicando cuál en cada caso y qué razones hay para determinarlo.
Problema 7 Guiándose por los ejemplos de las funciones del Problema 6:
- Propongan la fórmula de una función exponencial tal que y tal que .
Solución:
- Propongan la fórmula de una función exponencial tal que y tal que .
Solución:
- Propongan la fórmula de una función exponencial tal que y tal que .
Solución:
- Propongan la fórmula de una función exponencial tal que y tal que .
Solución:
Problema 8 Lean el siguiente recuadro:
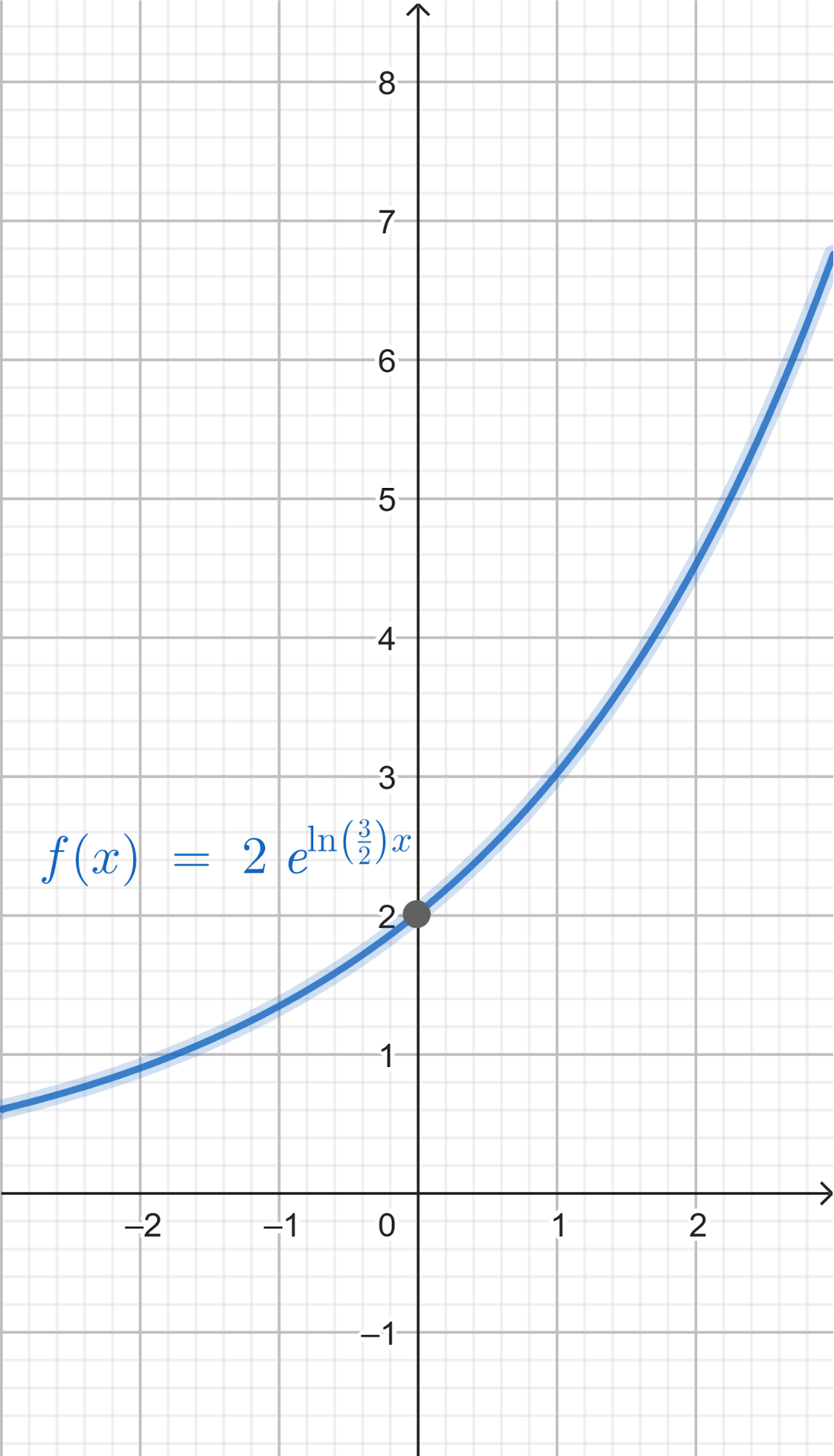
En la mayoría de las aplicaciones de la física y de la ingeniería -y también en los libros de cálculo a los que puedan acceder- seguramente encontrarán funciones exponenciales expresadas de una manera distinta a la que hemos utilizado hasta ahora. En vez de escribir la fórmula de una función exponencial de la manera: Donde a es algún número real distinto de 0, y , las funciones exponenciales aparecen presentadas con este aspecto: Donde a sigue siendo algún número real distinto de 0 y k también lo es. Pero la letra que aparece como base en la expresión de la función exponencial no representa a un número cualquiera, sino al número que en el Problema 20 de la Unidad se define como: ¿Por qué elegir este número tan particular como base de las potencias en las funciones exponenciales? Para responder esta pregunta habrá que esperar hasta el Problema 12 de la Unidad 7. Mientras tanto, haremos bien en acostumbrarnos a verlo aparecer y usarlo. |
Utilicen propiedades de la potenciación (ver Problema 25) para escribir en la forma las funciones de la forma que aparecieron en los Problemas 2 y 5.
Problema 9 El precio de un automóvil usado disminuye con el tiempo, de manera que cada año cuesta el 15% menos de lo que costaba el año anterior. Consideren que un auto determinado cuesta hoy $100000.
- Dibujen a mano alzada un gráfico que describa la variación del costo del automóvil en función del tiempo y expliquen las decisiones que tomen al diseñar la forma del gráfico.
Solución:
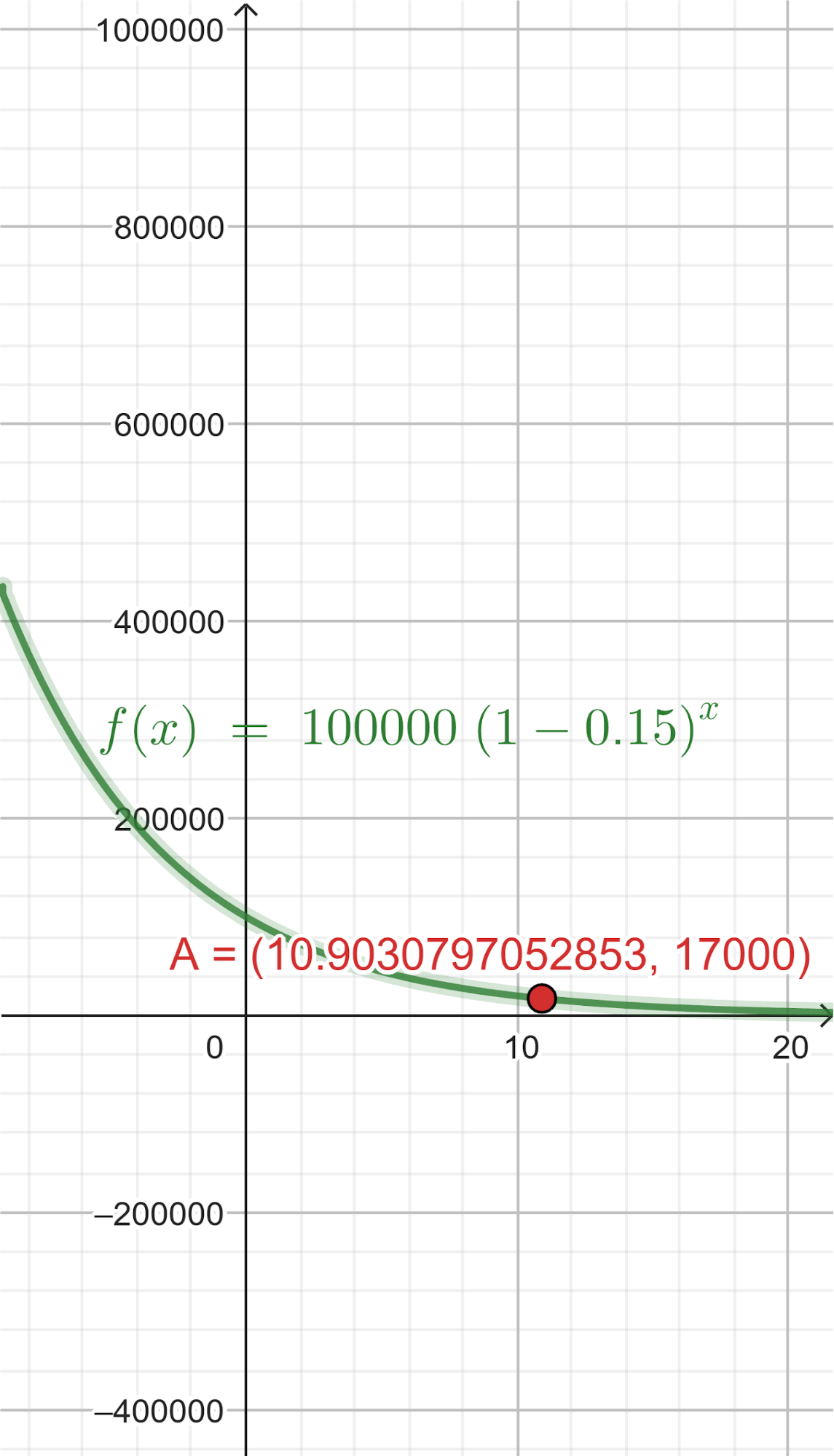
- Un comprador tiene ahorrados $17000. ¿Cuánto tiempo debería esperar, como mínimo, para poder comprar ese auto?.
Solución:
El comprador debe esperar casi 11 años para poder comprar.
Gráfica:
Este problema, junto con los problemas 3, 18, 15 y 16 están tomados del libro [9].
Problema 10 Este problema es un experimento para hacer entre todos en la clase. El docente irá registrando la información en el pizarrón. Lean atentamente las indicaciones:
En los siguientes gráficos la variable dependiente es función del tiempo t. Es decir, los gráficos corresponden a ciertas cantidades que van disminuyendo con el tiempo t.
- Consideren el Gráfico 1
- Elijan un punto concreto en el gráfico.
- Interpreten en el gráfico cuánto tiempo debe pasar para que la cantidad del punto que eligieron se reduzca a la mitad.
- Vuelquen la información en una tabla como la siguiente y pasensela a su docente:
Punto Inicial | Punto Final | Tiempo Transcurrido |
Gráfico 1 |
- Consideren el Gráfico 2
- Elijan un punto concreto en el gráfico.
- Interpreten en el gráfico cuánto tiempo debe pasar para que la cantidad del punto que eligieron se reduzca a la mitad.
- Vuelquen la información en una tabla como la siguiente y pasensela a su docente:
Punto Inicial | Punto Final | Tiempo Transcurrido |
Gráfico 2 |
- Consideren el Gráfico 3
- Elijan un punto concreto en el gráfico.
- Interpreten en el gráfico cuánto tiempo debe pasar para que la cantidad del punto que eligieron se reduzca a la mitad.
- Vuelquen la información en una tabla como la siguiente y pasensela a su docente:
Punto Inicial | Punto Final | Tiempo Transcurrido |
Gráfico 3 |
Problema 11 Lean el siguiente recuadro:
Cuando una cantidad decrece exponencialmente con el tiempo t, es decir , con y , el tiempo que le lleva a una cantidad reducirse a la mitad es siempre el mismo (No depende del valor ni de cuál sea el instante y se llama vida media. La siguiente situación muestra un ejemplo del concepto. |
La vida media de la nicotina en la sangre es de unas 2 horas. Una persona absorbe alrededor de 0.4 mg de nicotina en el torrente sanguíneo al fumar un cigarrillo común y corriente.
- Llenen los espacios de la siguiente tabla con la cantidad de nicotina restante en la sangre después de t horas.
Solución:
- Estimen el lapso de tiempo que habría que esperar para que la cantidad de nicotina se reduzca a 0.04 mg.
Solución:
t (horas) | 0 | 2 | 4 | 6 | 8 | 10 |
Nicotina (mg) | 0.4 | 0.2 | 0.1 | 0.05 | 0.025 | 0.0125 |
Problema 12 ¿Puede existir una función exponencial de la forma que pase por los siguientes puntos? Expliquen.
- Solución: No se puede porque y2 es negativa ya que ln(-2) no se encuentra en los reales
Solución:
Armamos un sistema de ecuaciones, aplicamos logaritmo neperiano y restamos ecuaciones.
Dividimos 2 por 1:
Aplicamos Logaritmo neperiano a ambos lados.
Por propiedad de Logaritmo
Reemplazamos en alguna ecuación para hallar
Por lo cual la función es:
o
Solución:
Armamos un sistema de ecuaciones, aplicamos logaritmo neperiano y restamos ecuaciones.
Dividimos 2 por 1:
Aplicamos Logaritmo neperiano a ambos lados.
Por propiedad de Logaritmo
Reemplazamos en alguna ecuación para hallar
Reemplazamos en alguna de las ecuaciones para averiguar :
Por lo cual la función es:
o
Problema 13 Encuentren, si existe, una función exponencial que verifique las condiciones pedidas en cada caso:
- Que sea decreciente y su imagen sea .
Solución:
- Que sea creciente y su imagen sea .
Solución:
- Que sea decreciente y su imagen sea .
Solución:
- Que sea decreciente y su ordenada al origen sea -3.
Solución:
- Que sea creciente y su imagen sea .
Solución:
Problema 14
- Encuentren los parámetros a y b para que la ecuación de la forma se corresponda con cada una de las gráficas que se muestran a continuación.
- Hagan lo mismo, pero para una función de la forma .
Solución:
Problema 15 En un laboratorio se está estudiando un tipo de bacterias que se reproducen por bipartición cada 15 minutos. Se inicia un campo de cultivo con una bacteria a las 9:00 horas. Mediante el microscopio, se observa que a las 11:45, el campo de estudio tiene llena la mitad de su capacidad.
- ¿A qué hora se llenará el campo de cultivo?.
- ¿Cuántas bacterias habrá cuando el campo de cultivo esté lleno?.
- Escriban la fórmula de la función que describe este fenómeno y determinen su dominio.
Problema 16 La función que describe el número de bacterias en un cultivo para cada momento, después de iniciado el mismo, viene dada por la fórmula:
Donde el tiempo t se mide en minutos.
- Construyan una tabla de valores y un gráfico para algunos valores de t.
- Interpreten el significado del 5, el 2 y el 30 que aparecen en la fórmula.
- ¿Cuántas horas deben transcurrir para que la población supere las 500000 bacterias?.
- ¿Qué ventaja tiene que en la fórmula de esta función la base de la potencia sea 2 en vez de ? Más adelante veremos ventajas de elegir a como base.
Problema 17 Hallen los valores de que verifiquen las siguientes igualdades:
Problema 18 Lean el siguiente texto:
Decaimiento radiactivo Durante toda su vida las plantas y animales incorporan a su organismos, a través del aire que respiran y de los alimentos que ingieren, distintos elementos presentes en la atmósfera. Entre ellos está el carbono. Toda concentración de carbono de la atmósfera tiene una parte estable (Carbono 12 o ) y una parte radiactiva (Carbono 14 o ). La cantidad de presente en un organismo va decayendo, pero también es renovada continuamente mientras el organismo vive, de manera que su proporción de es constante. Cuando el organismo muere, ya no renueva su proporción de . Mientras la cantidad de , permanece estable en él, el continúa decayendo en función del tiempo. Los científicos han podido comprobar que la vida media del es 5730 años, es decir, que la concentración de se reduce a la mitad cada 5730 años. |
- Supongan que la concentración de El carbono presente en un organismo es cierto número K. Escriban la fórmula que permite calcular la concentración de en dicho organismo, en función del tiempo (medido en años), a partir del momento en que el organismo muere.
- Grafiquen la función.
- Los investigadores que estudiaron las pinturas rupestres de las cuevas de Altamira pudieron medir la proporción de (Tal vez en las sustancias orgánicas de la pintura o en otros restos orgánicos hallados en las cuevas) y determinaron que sólo quedaba el 20% de la concentración inicial K. ¿Cómo pueden utilizar esta información para determinar la antigüedad de las pinturas?.
Problema 19 Una sustancia radiactiva se desintegra de tal manera que la cantidad de masa que permanece después de t días se expresa mediante la función.
Donde se mide en kilogramos.
- Encuentren la masa inicial.
- ¿Cuánta masa permanece después de 45 días?.
- ¿Cuánto tiempo debe pasar para que haya una masa de 5 kg?.
Problema 20 Determinen si cada una de las siguientes tablas de valores podría corresponder a una función lineal, una función exponencial, o ninguna de ellas. Para cada tabla de valores que podría corresponder a una función lineal o una exponencial, encuentre una fórmula para la función.
x | f(x) | t | f(t) | u | g(u) | ||
0 | 10.5 | -1 | 50.2 | 0 | 27 | ||
1 | 12.5 | 0 | 30.12 | 2 | 24 | ||
2 | 18.9 | 1 | 18.072 | 4 | 21 | ||
3 | 36.7 | 2 | 10.8432 | 6 | 18 |
Problema 21 La figura ilustra gráficas de poblaciones de varias ciudades en función del tiempo. Relacionen cada una de las siguientes descripciones con una gráfica y expliquen por qué.
- La población de la ciudad aumentó en 5% por año.
- La población de la ciudad aumentó en 8% por año.
- La población de la ciudad aumentó en 5000 personas por año.
- La población de la ciudad permaneció estable.
Problema 22 En el Problema 1 se estudió un modelo de crecimiento de población, obteniéndose la función:
Que indica el número de habitantes, en función del tiempo t, medido en años.
- Según el modelo, ¿Cúal era la población en el momento inicial?.
- ¿Cuánto tiempo deberá pasar para que la población se duplique?.
- ¿Cuánto deberá pasar para que llegue a 10000 habitantes?.
- Elijan una escala adecuada para los ejes y construyan una gráfica donde la población se represente en el eje de abscisas y el tiempo en el eje de ordenadas, que muestre el tiempo transcurrido en función de la población presente en el pueblo.
Problema 23 En el problema anterior se planteó la dificultad de conocer el valor de t, conocido el valor de . La dificultad consiste en que la incógnita t ocupa el lugar del exponente. Vamos a plantear una situación similar, pero con números más cómodos, para enfocar mejor el problema.
- Calculen en cada caso (Estimando o tanteando con la calculadora) el valor de x:
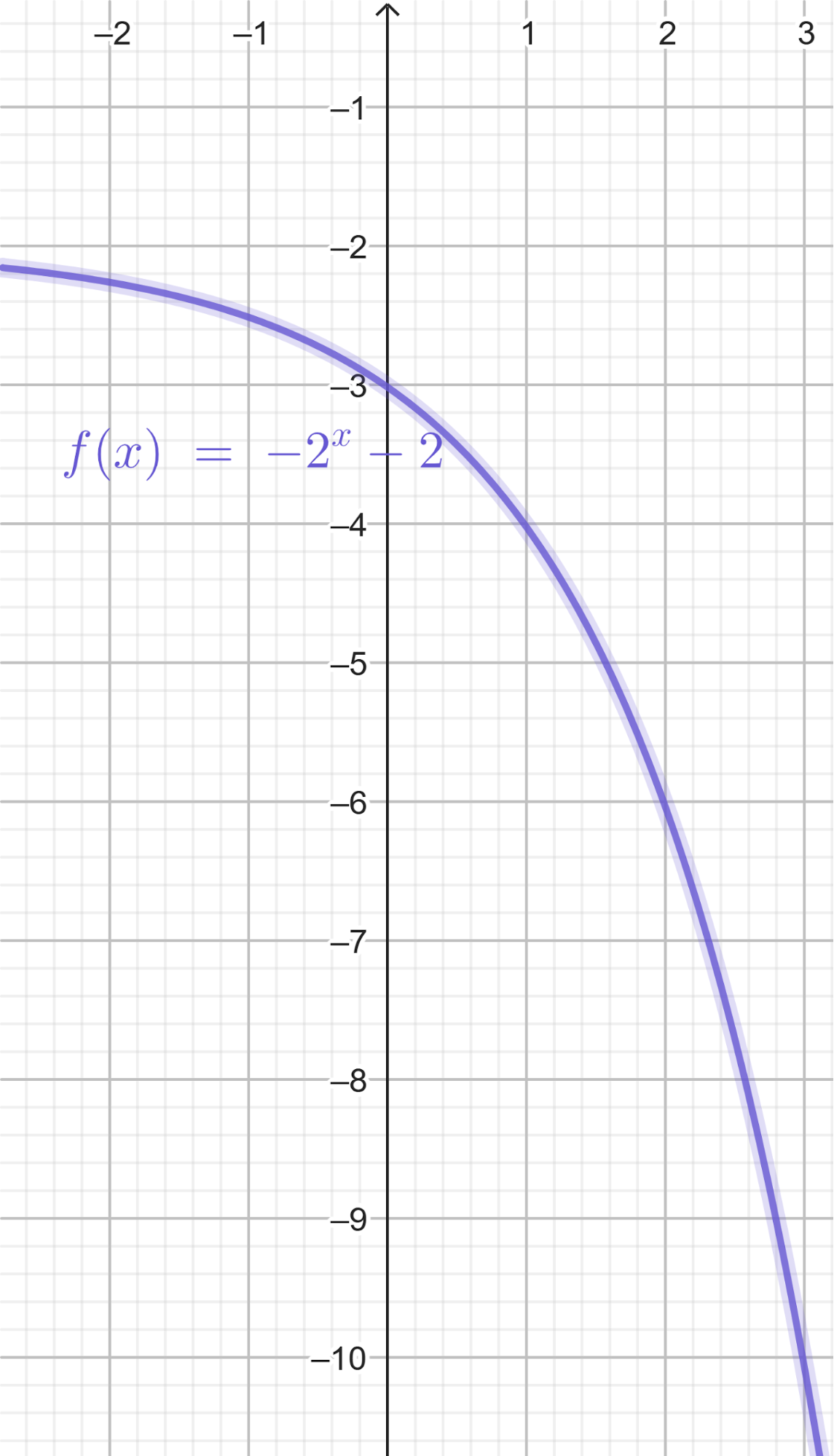
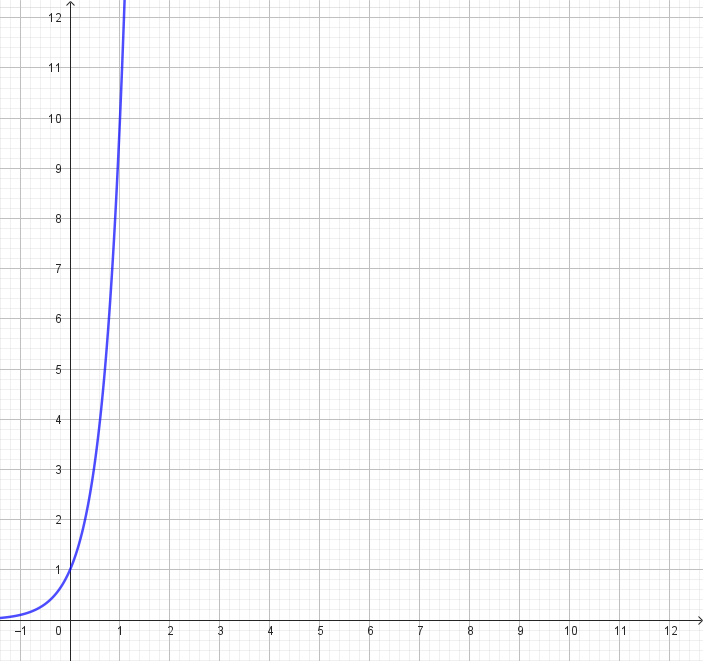
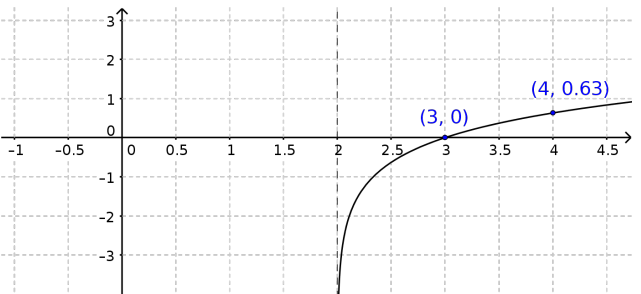
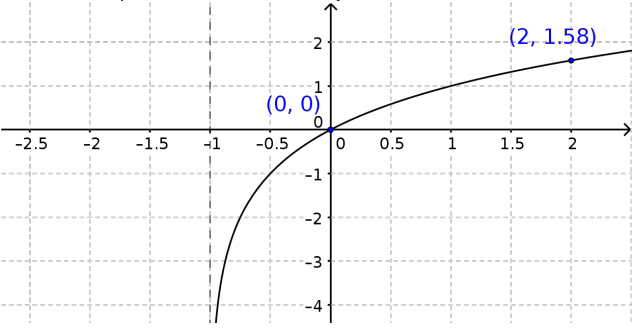
- El gráfico corresponde a la función . ¿Cómo pueden usarlo para verificar sus cálculos anteriores?.
- En el mismo sistema de coordenadas, grafiquen la función que, dado un número positivo x, indica a qué potencia debe elevarse el 10 para obtener x como resultado.
Problema 24 Lean el siguiente recuadro:
Definimos la función logaritmo en base 10 de un número x (Con el símbolo ) como la inversa de la función exponencial . Es decir, Es la potencia a la que hay que elevar el número 10 para obtener x. En símbolos: Observaciones:
|
Investiguen, usando una calculadora científica, para qué valores de x se obtiene cada uno de los resultados que se indican a continuación y luego expliquenlo a partir de la definición de .
- es un número entero.
- .
- es positivo.
- es negativo.
- tiene un desarrollo decimal cuya parte entera vale 4.
- tiene un desarrollo decimal cuya parte entera vale n, para cada número natural n.
- no existe (La calculadora devuelve algún mensaje de error).
Problema 25 Investiguen, haciendo experimentos con la calculadora, cuáles de las siguientes afirmaciones son falsas y cuáles (Según los experimentos) parecen ser verdaderas.
Problema 26 Investiguen, haciendo experimentos con la calculadora, cuáles de las siguientes afirmaciones son falsas y cuáles (Según los experimentos) parecen ser verdaderas.
Problema 27 Organicen un resumen con las propiedades válidas identificadas en los Problemas 25 y 26.
Problema 28 Lean el siguiente recuadro:
En toda la secuencia que va desde el Problema 24 hasta el Problema 27 se trabajó con la función logaritmo en base 10. Acá definimos la función cuando la base del logaritmo es el número : Definimos la función logaritmo en base de un número x (Con el símbolo ) como la inversa de la función exponencial . Es decir, es la potencia a la que hay que elevar el número para obtener x. En símbolos: o bien: Si: entonces Observaciones:
|
Adapten el resumen del Problema 27 a las funciones inversas y .
Problema 29 En el Problema 22 se trabajó con el modelo que da la cantidad de habitantes de un pueblo en función del tiempo. Definan, estableciendo claramente el dominio, la función inversa de aquella, es decir la que conociendo la población en un determinado momento informa cuánto tiempo ha transcurrido desde que el modelo comenzó a describir la población del pueblo.
Problema 30 Dadas las siguientes funciones logarítmicas:
- Grafiquen, determinando previamente el Dominio.
- Determinen el conjunto Imagen.
- Hallen, si posee, las intersecciones con los ejes.
- Indiquen si tiene asíntota y den su ecuación.
Problema 31 Encuentren los parámetros a y b para que la ecuación de la forma corresponda con cada una de las gráficas que se muestran a continuación.
Problema 32 Calculá sin usar calculadora (Ver Problema 24):
En los ítems a y b: ¿Qué condiciones debe tener el número a para que se pueda calcular el algoritmo?
Problema 33 Sabiendo que Calculen, en función de :
Problema 34 Relacionen cada función logarítmica con su gráfica.
Problema 35 Relean la definición de logaritmo en base 10 en el recuadro del Problema 24 y respondan:
- ¿Cómo definirían logaritmo en base 2?. Propongan ejemplos.
- ¿Cómo definirían logaritmo en base ?. Propongan ejemplos.