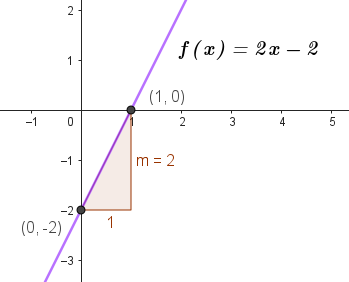
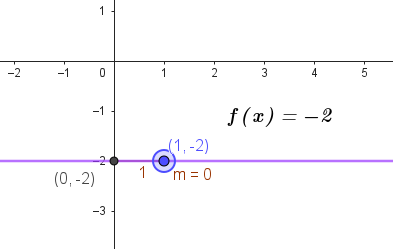
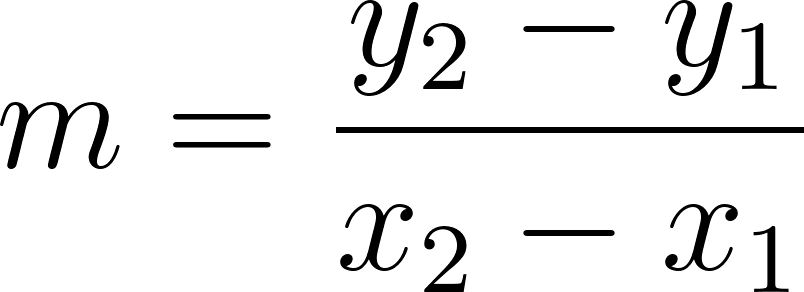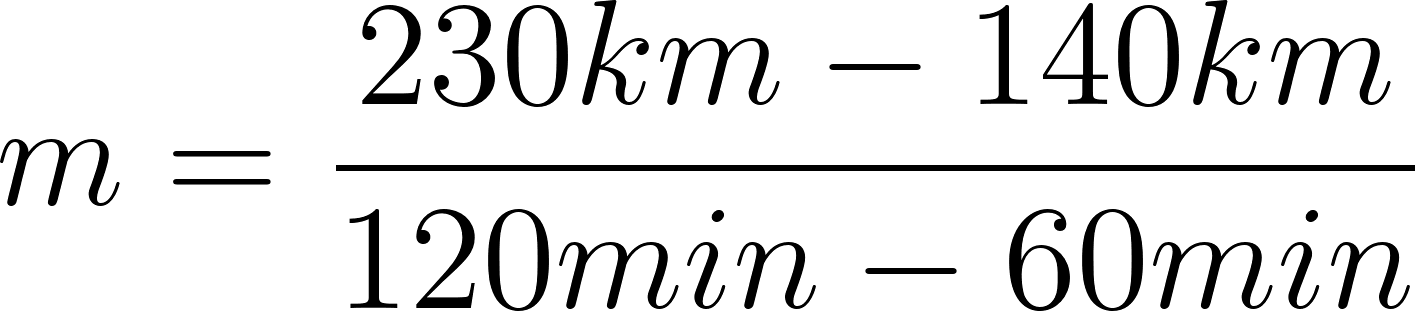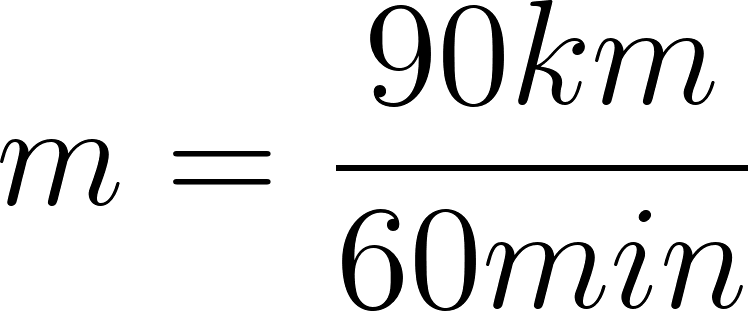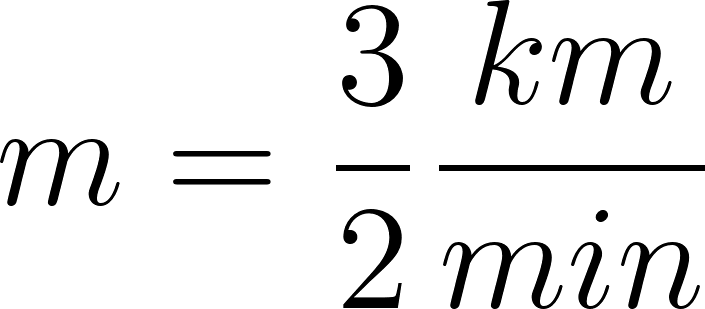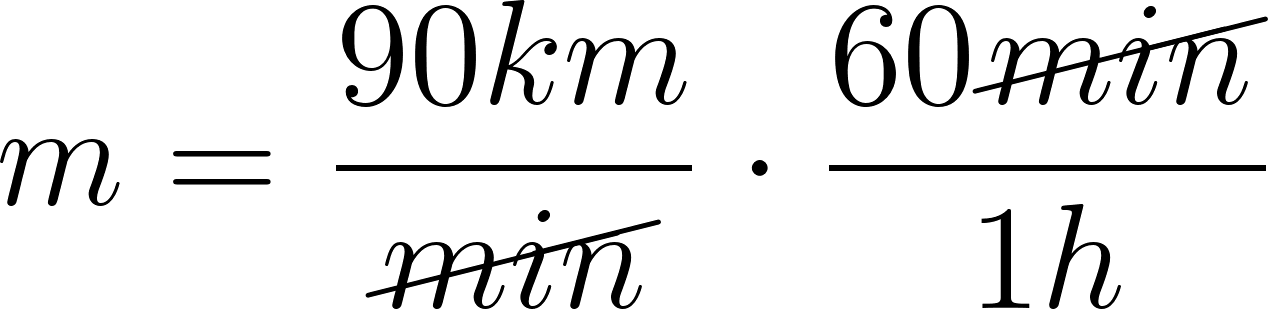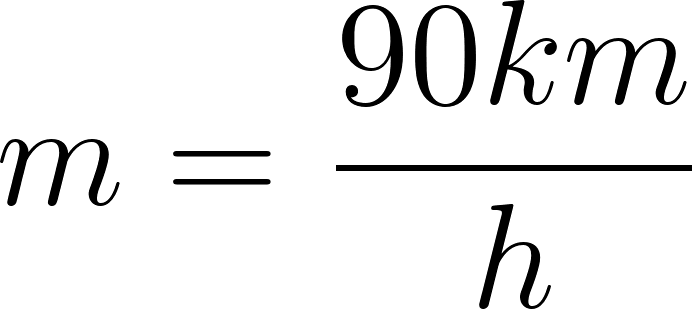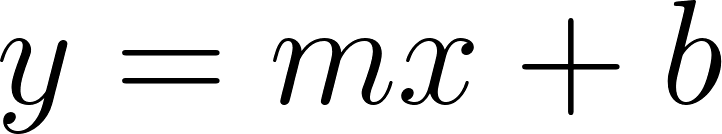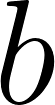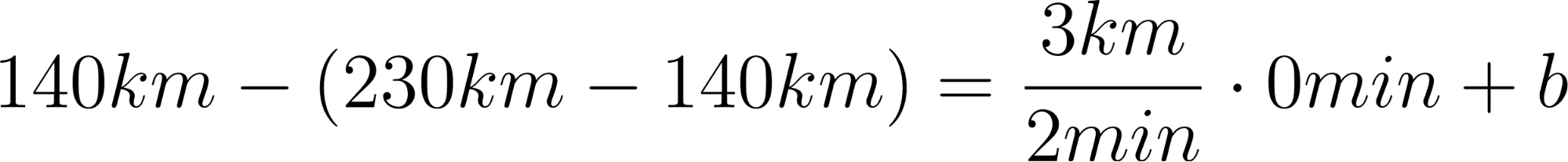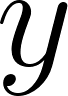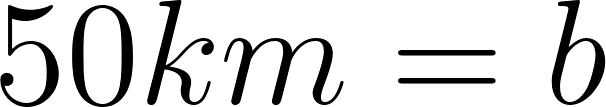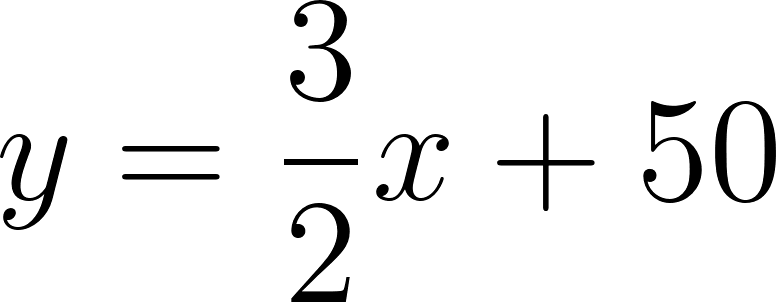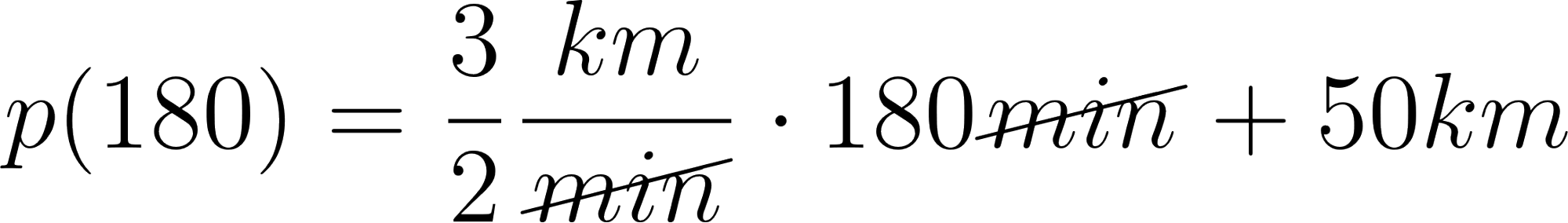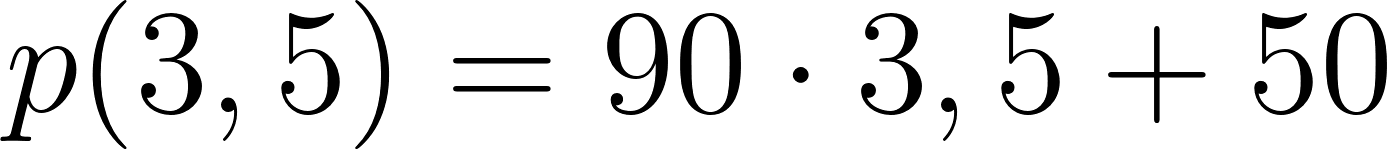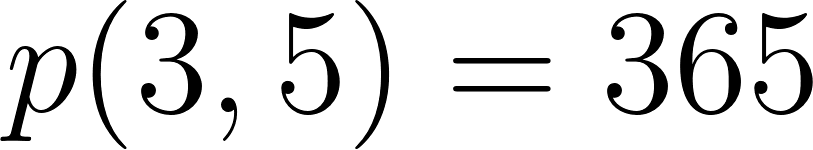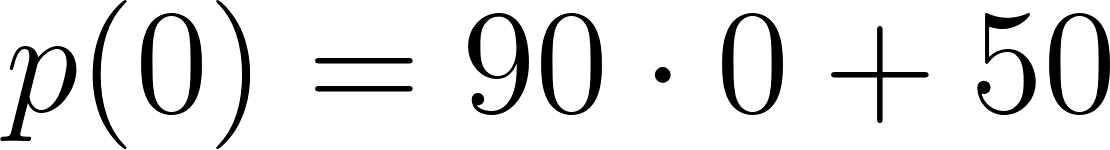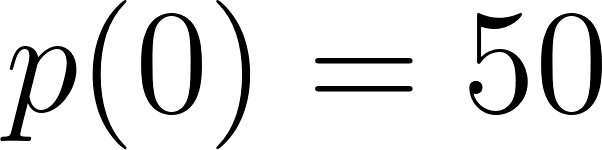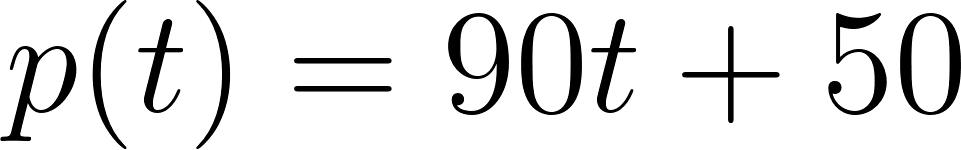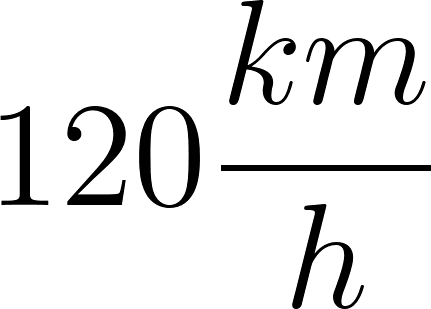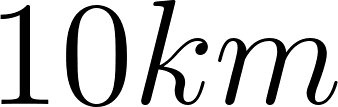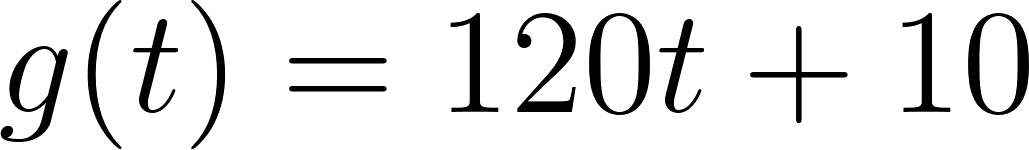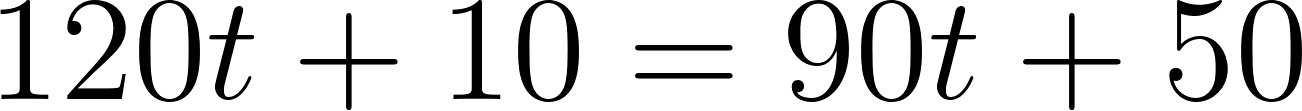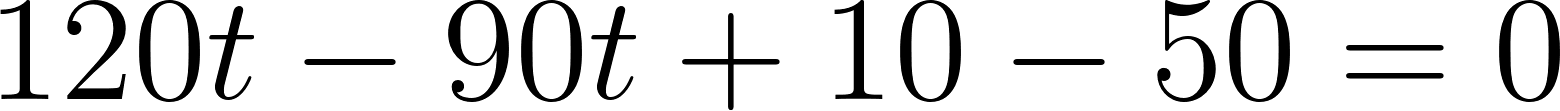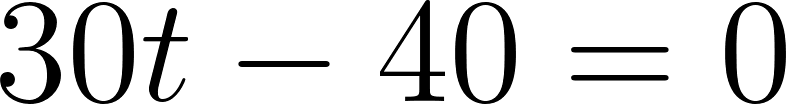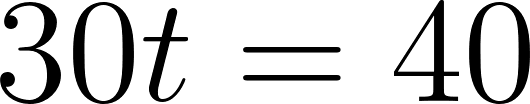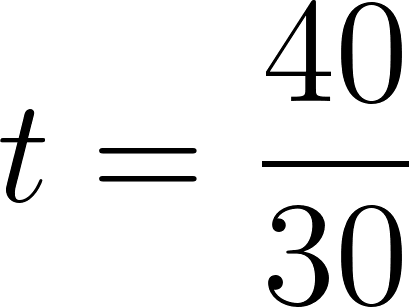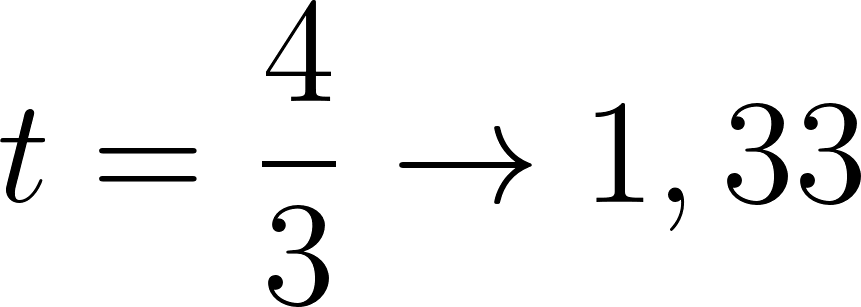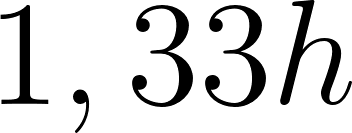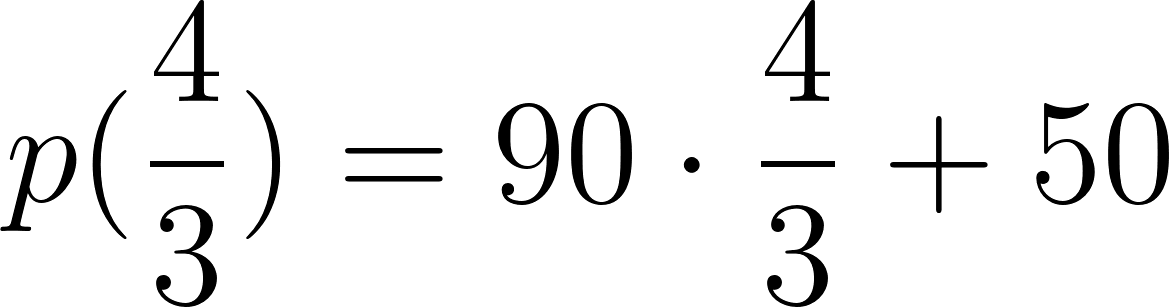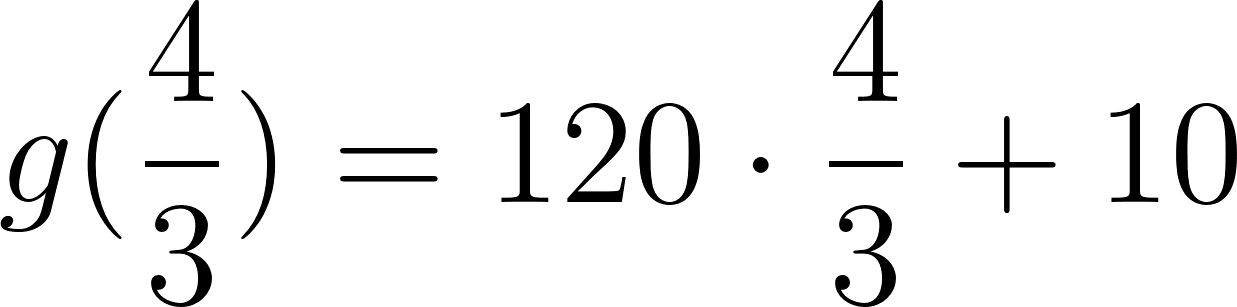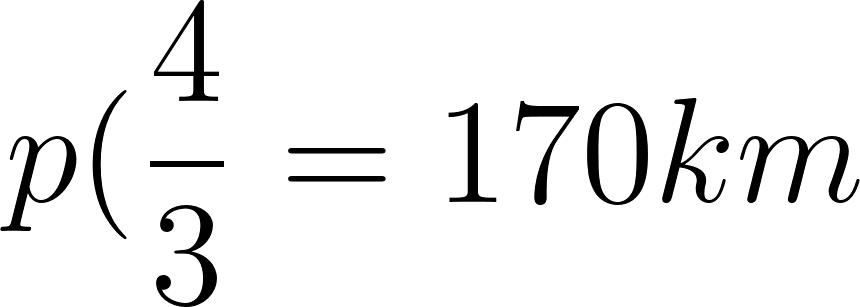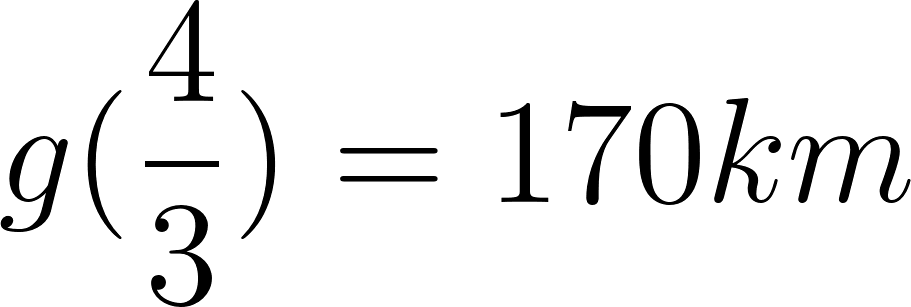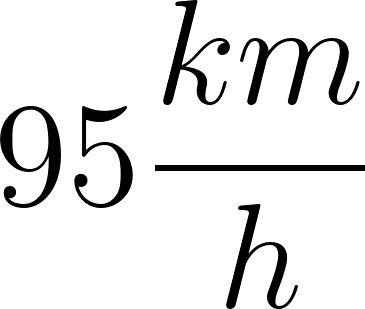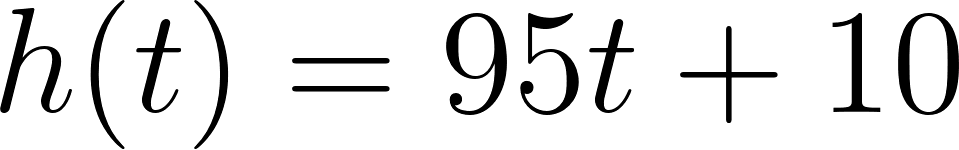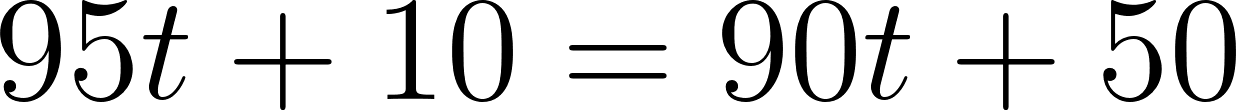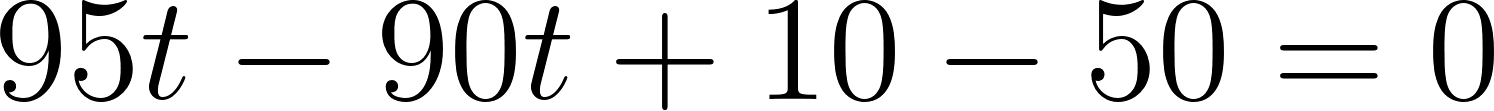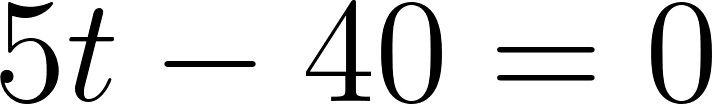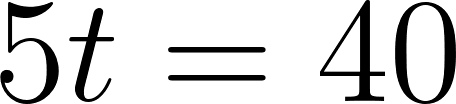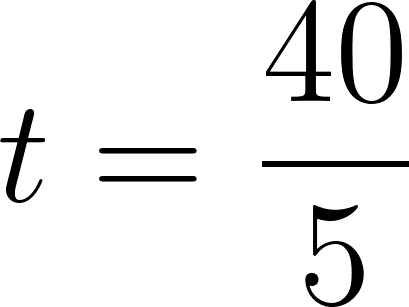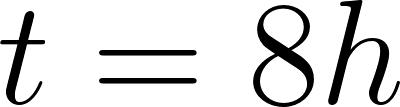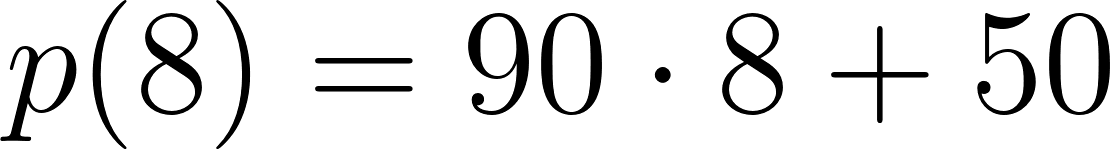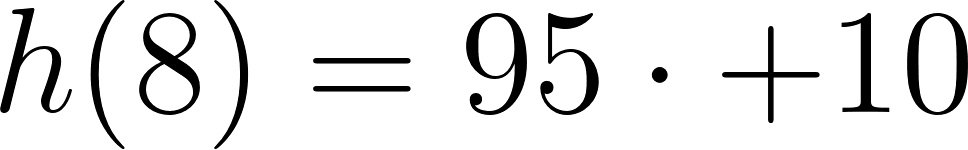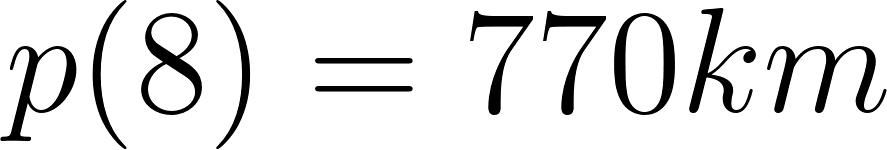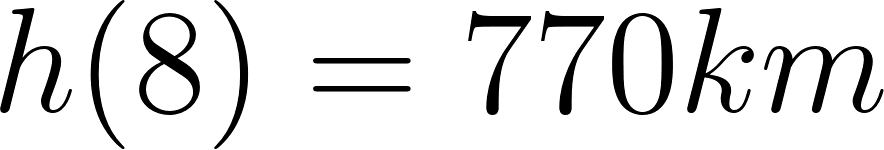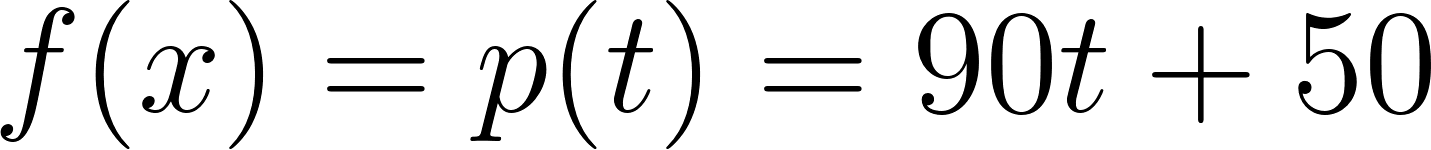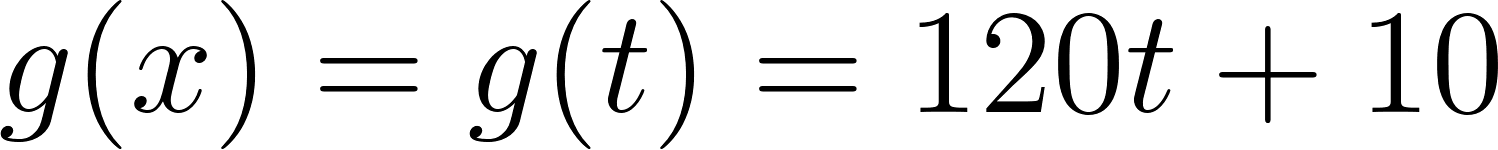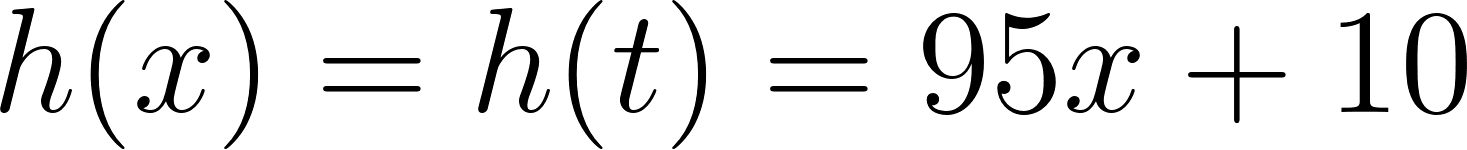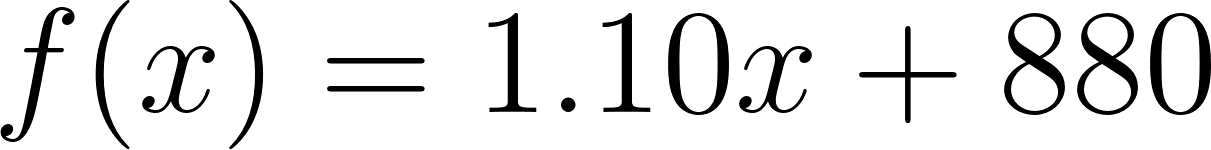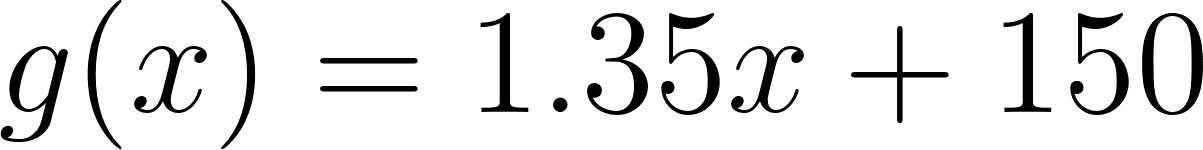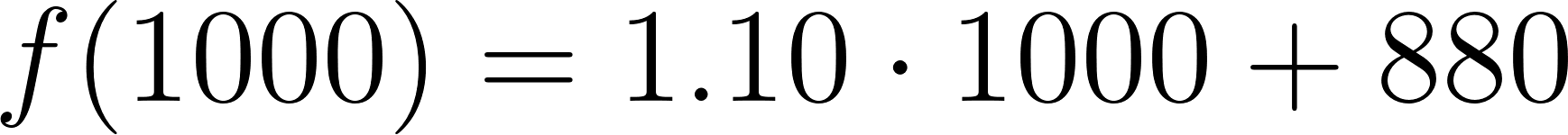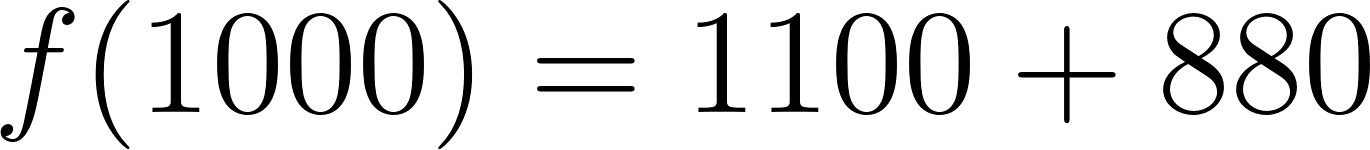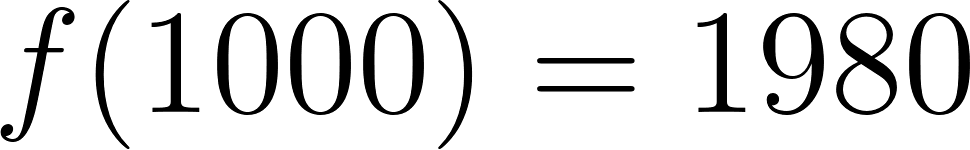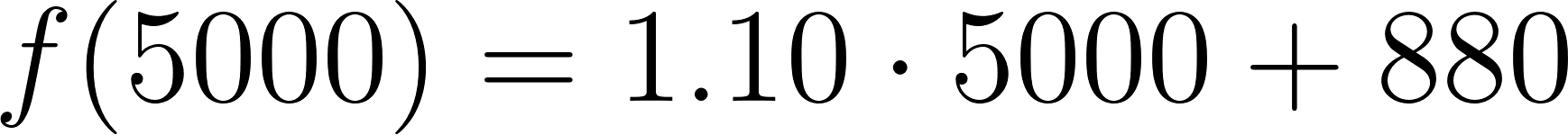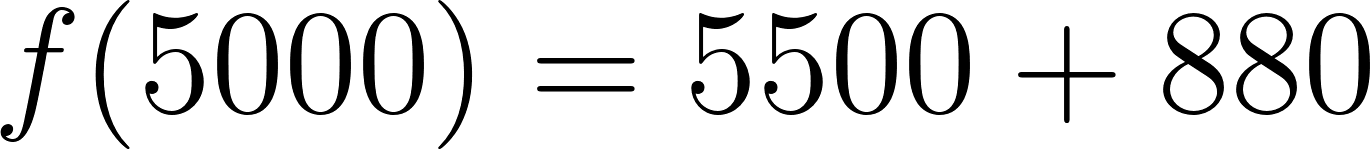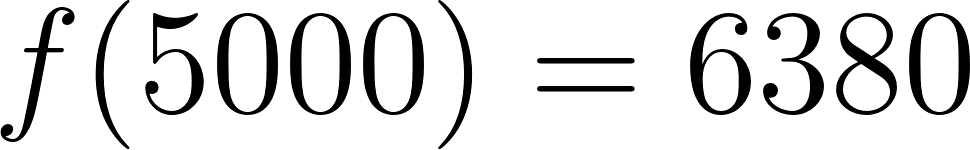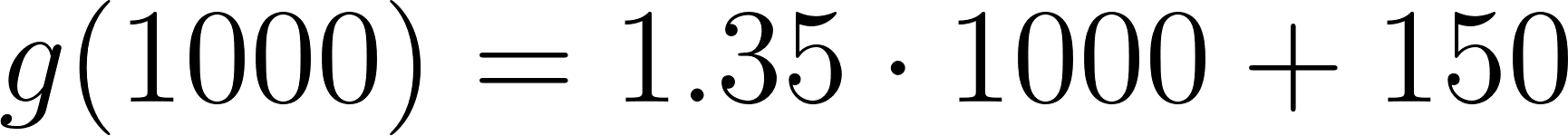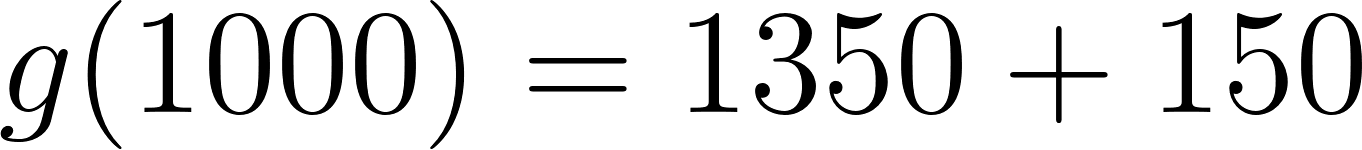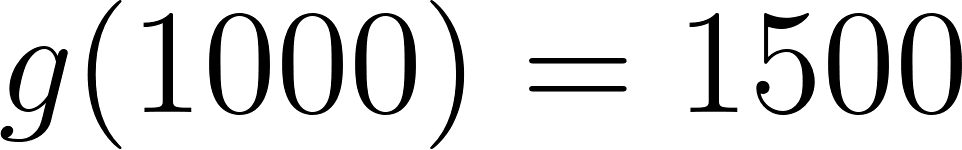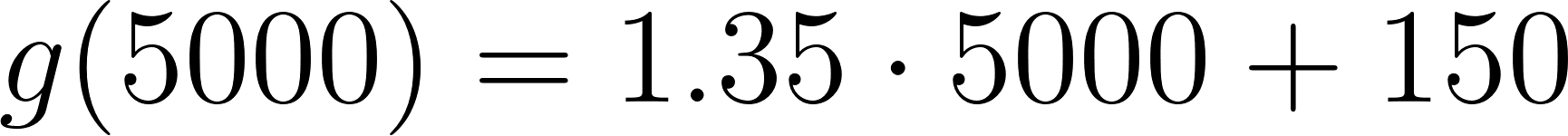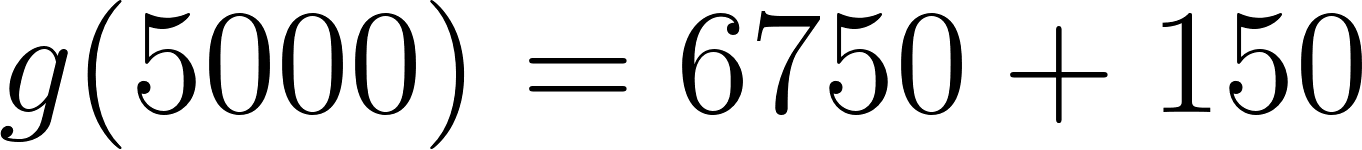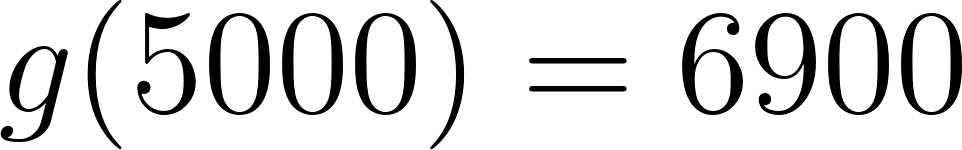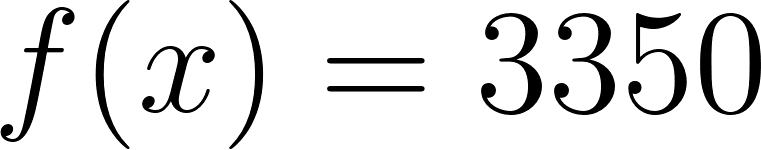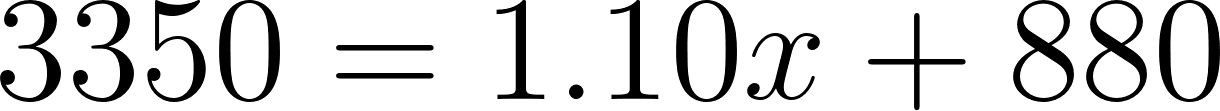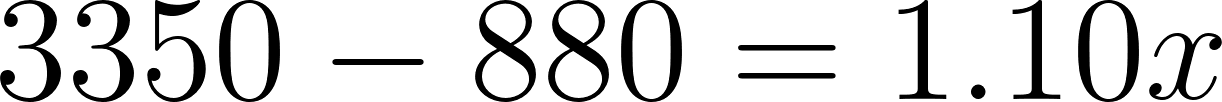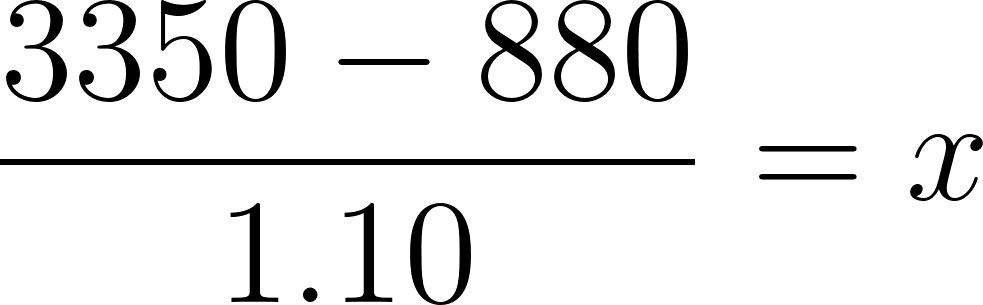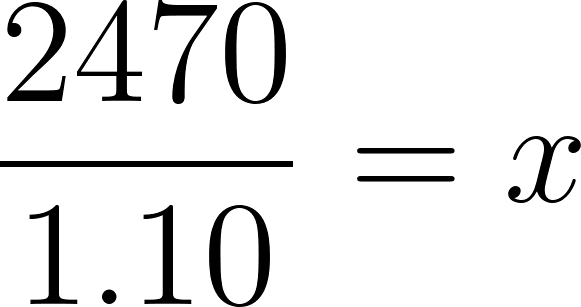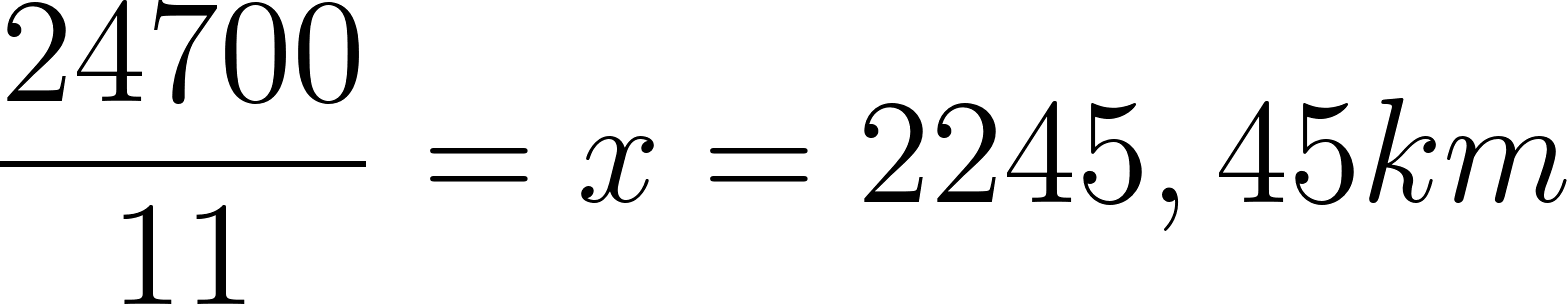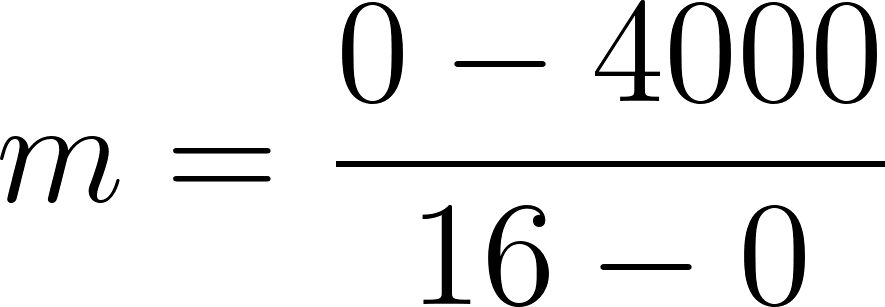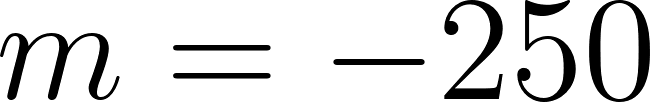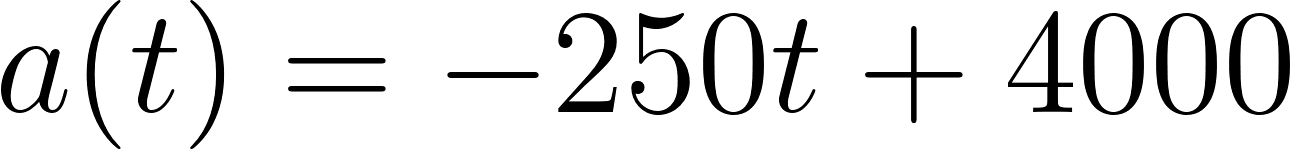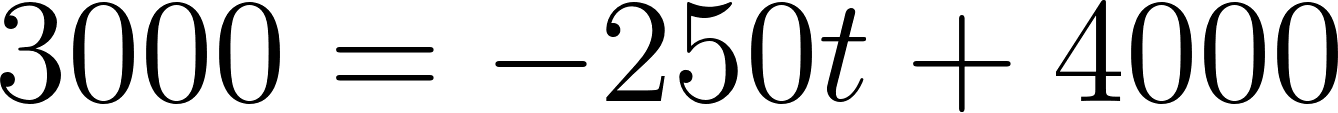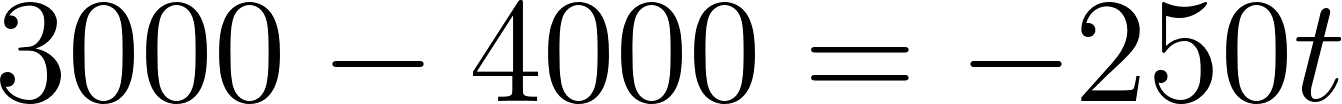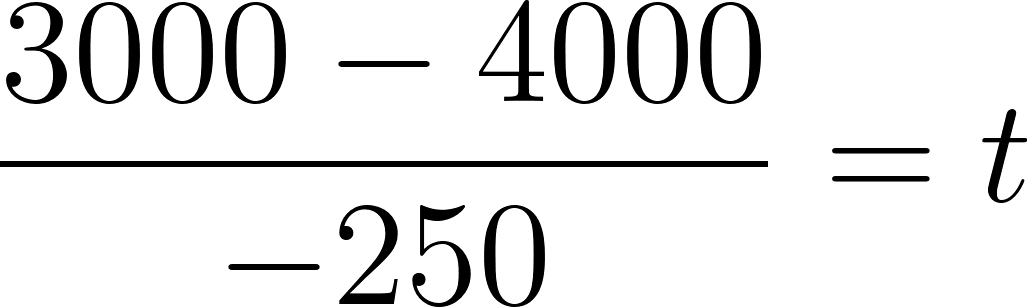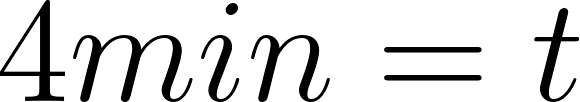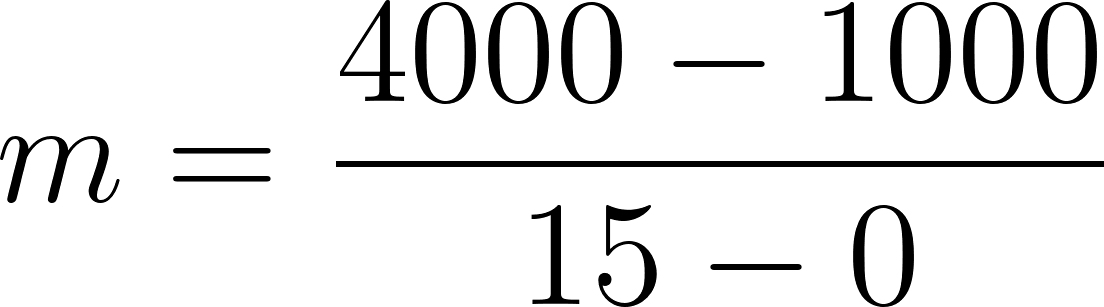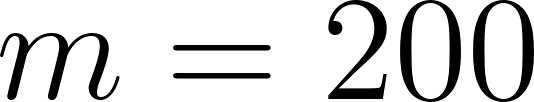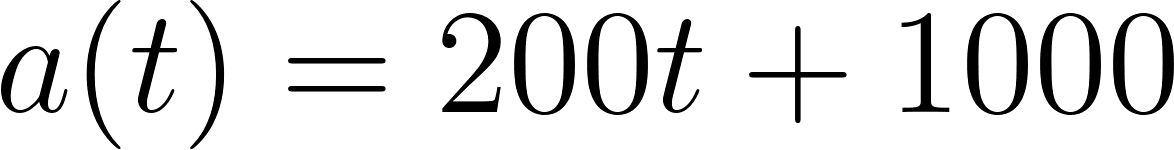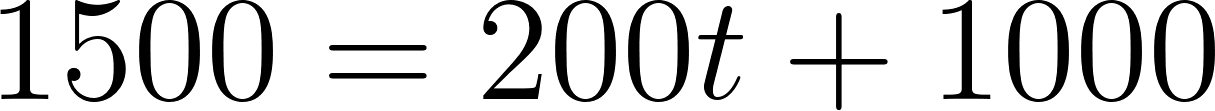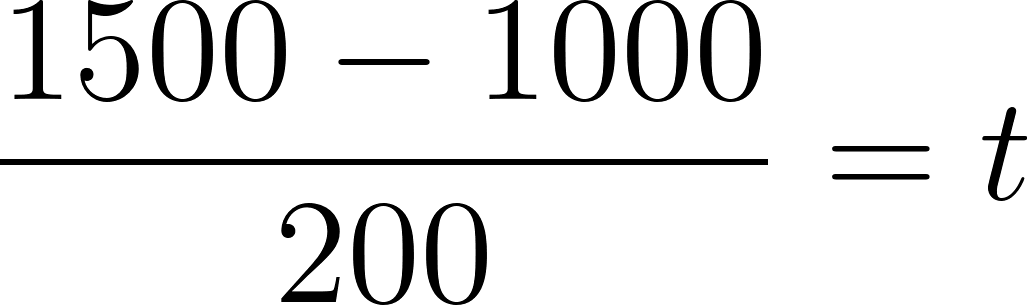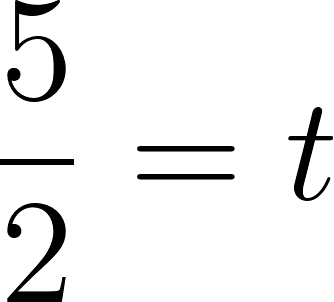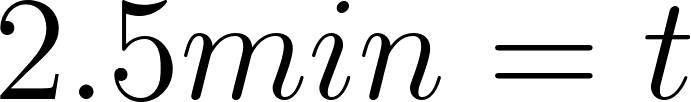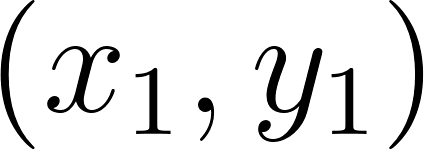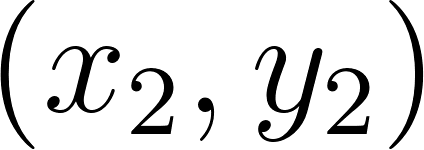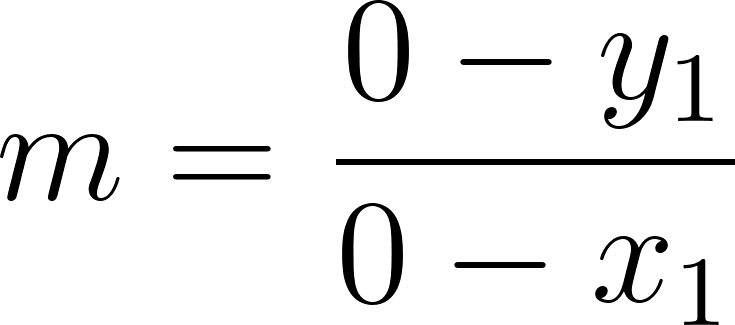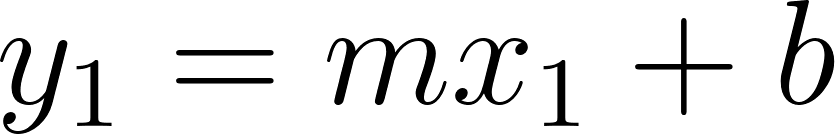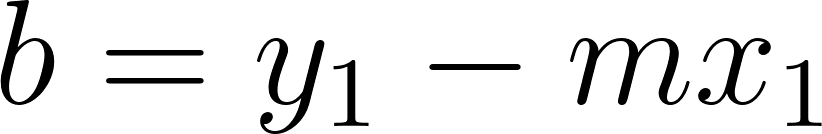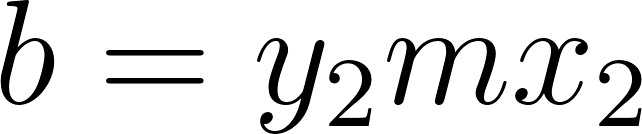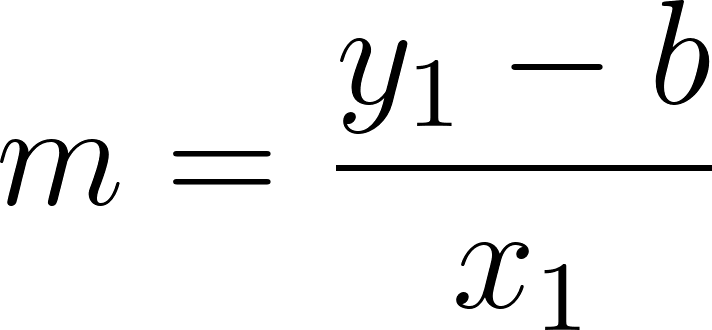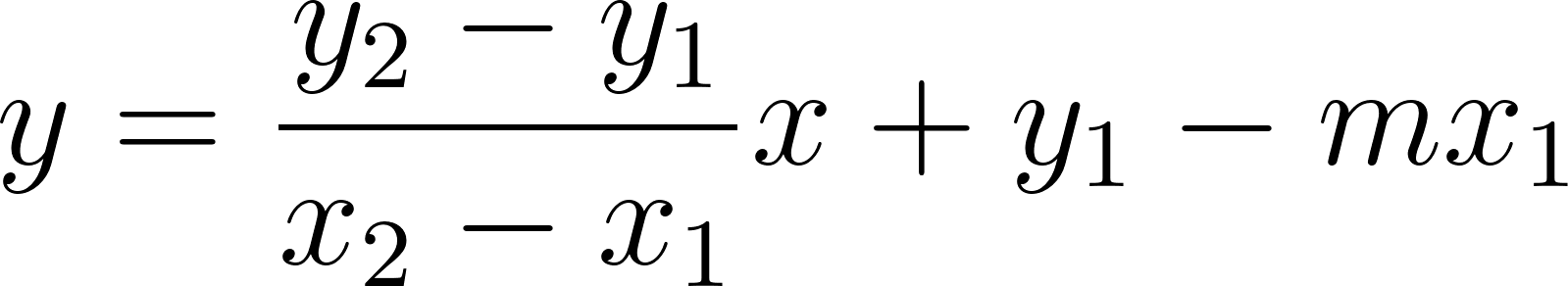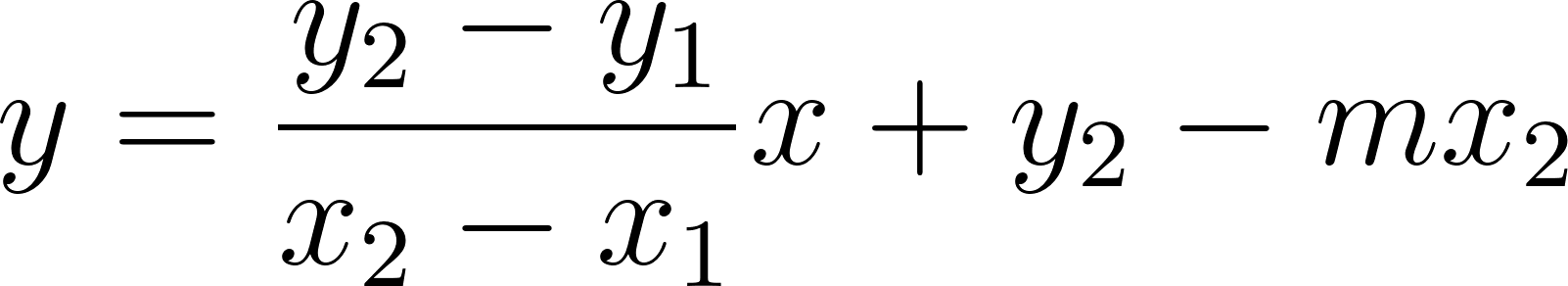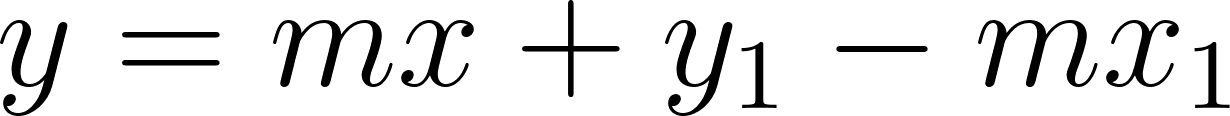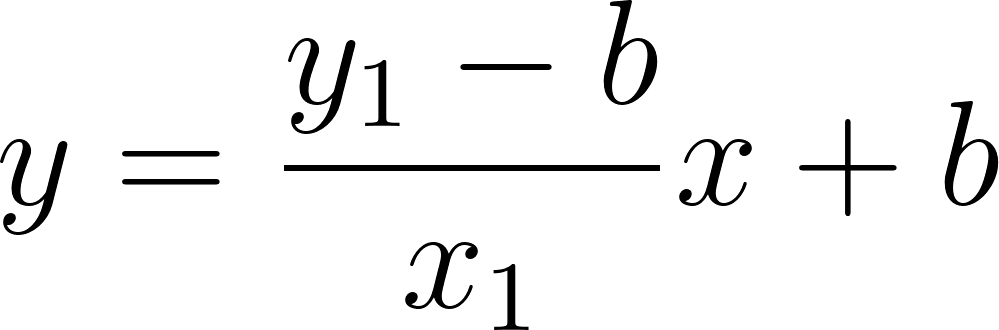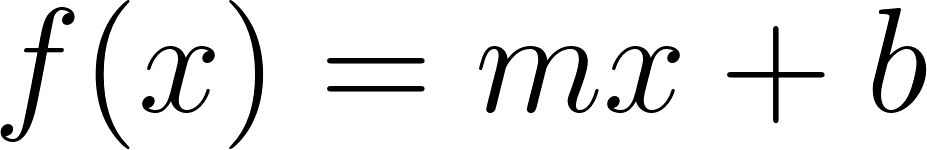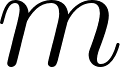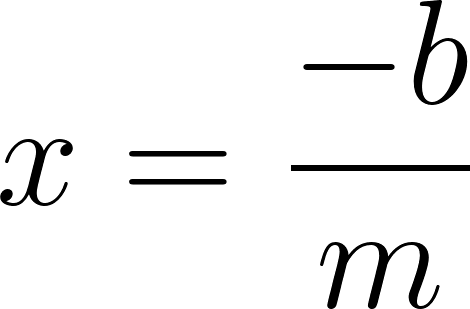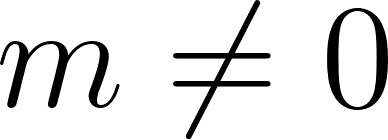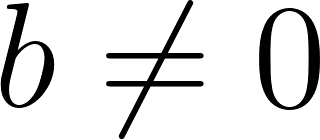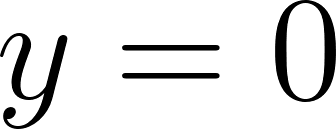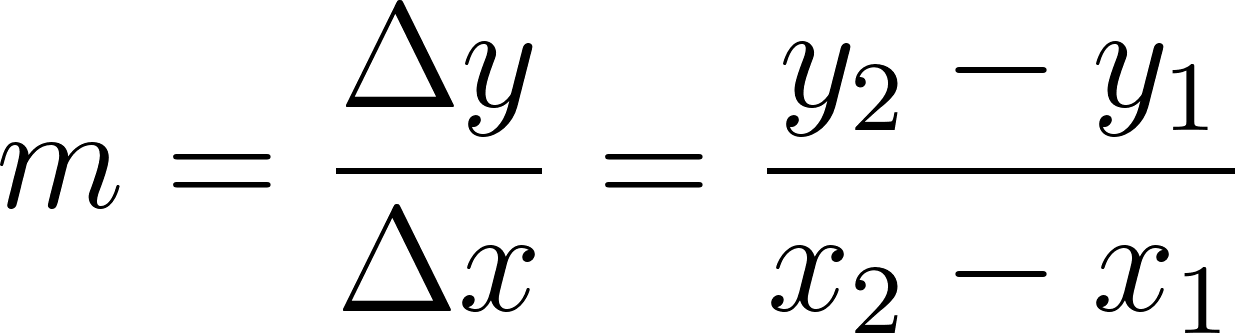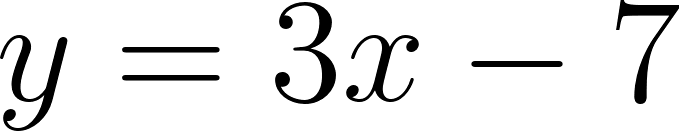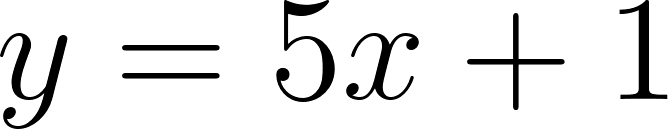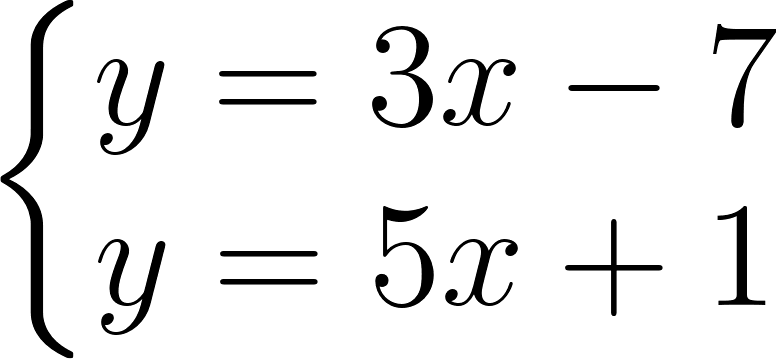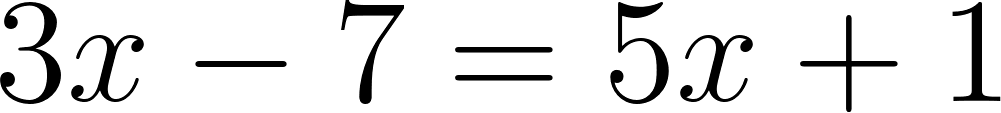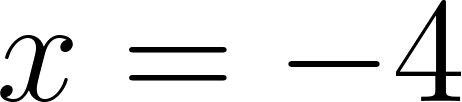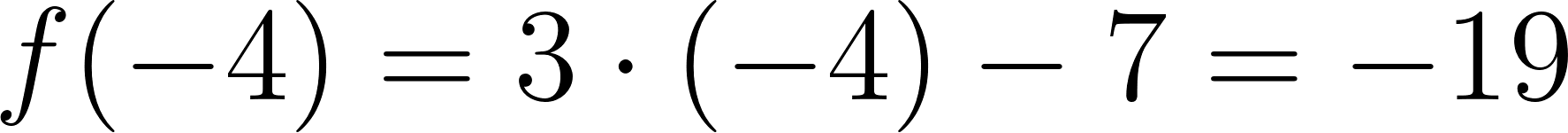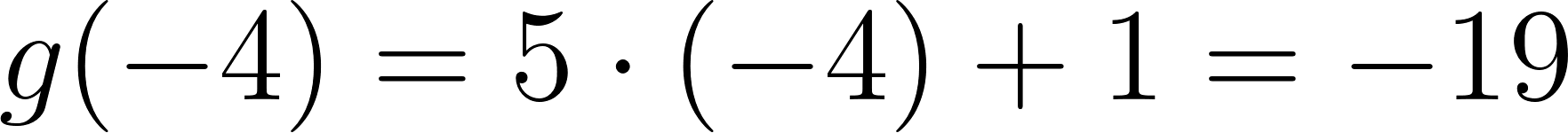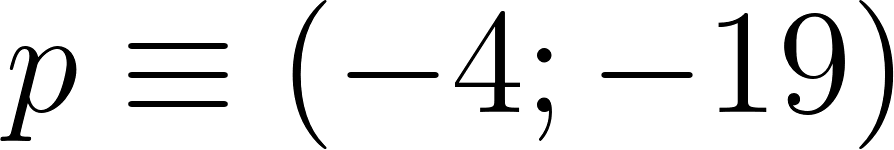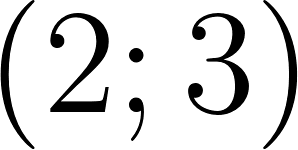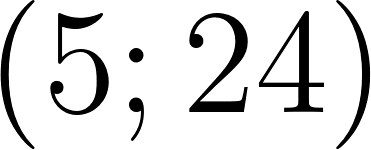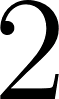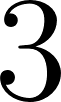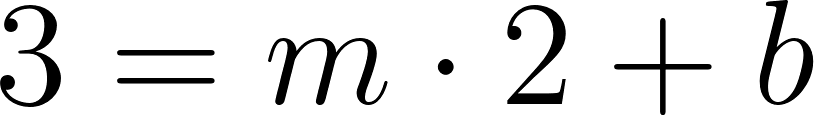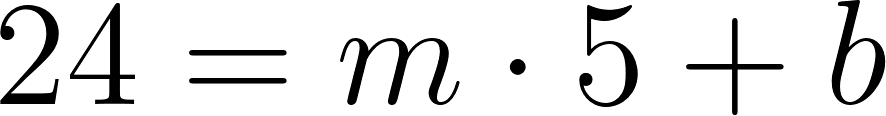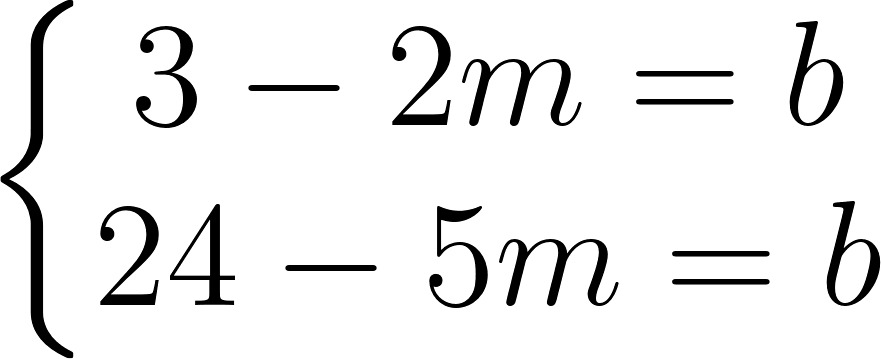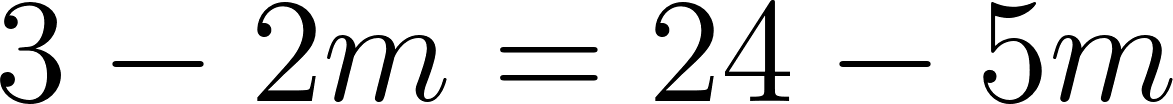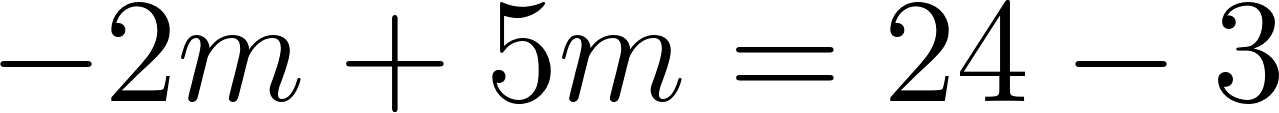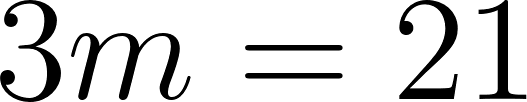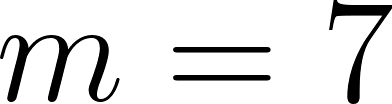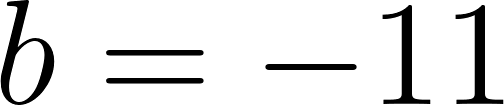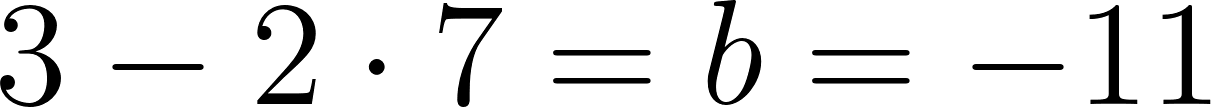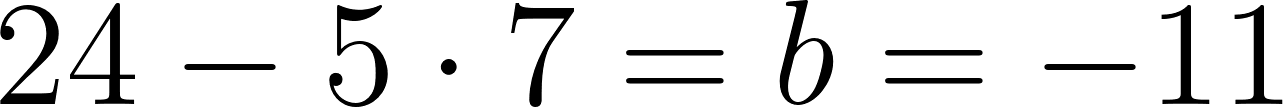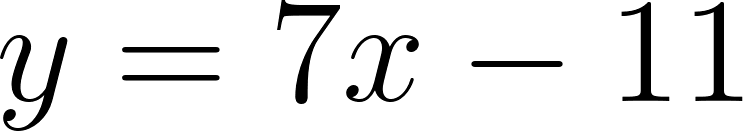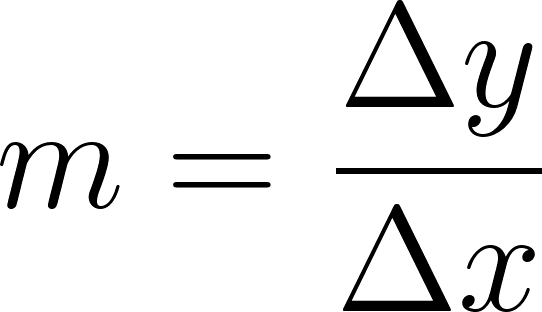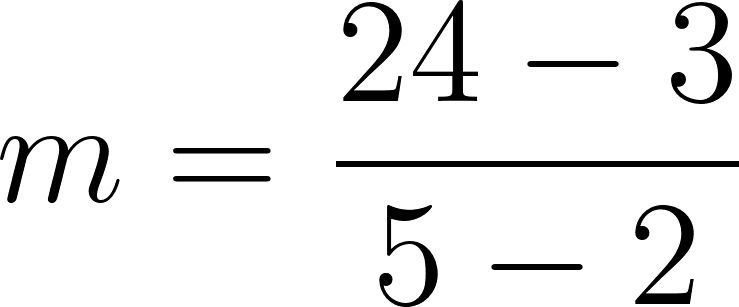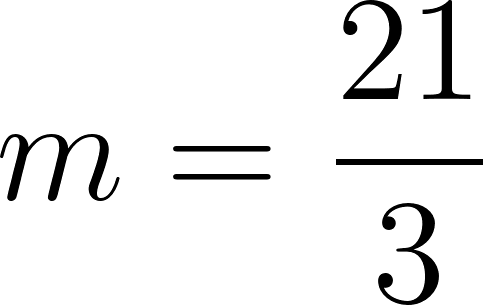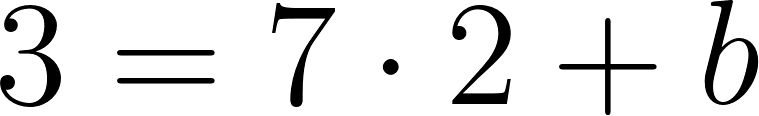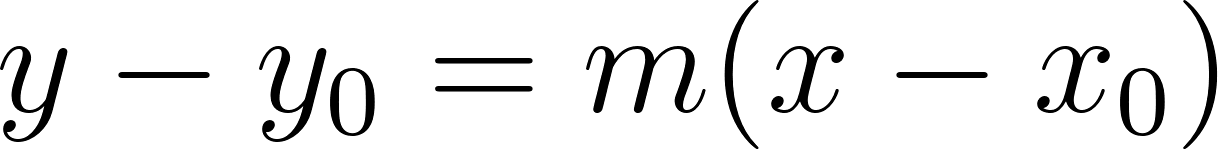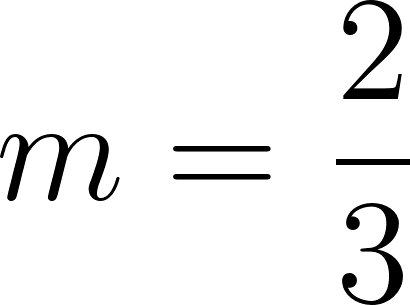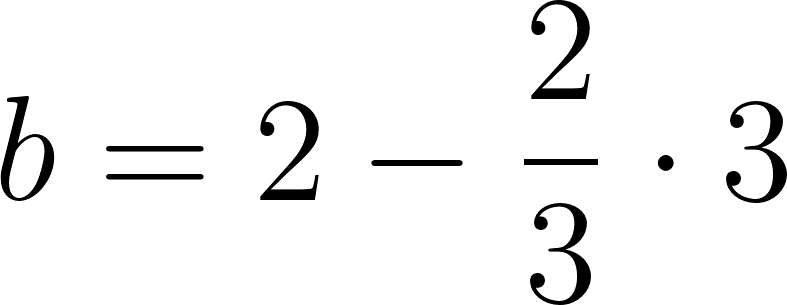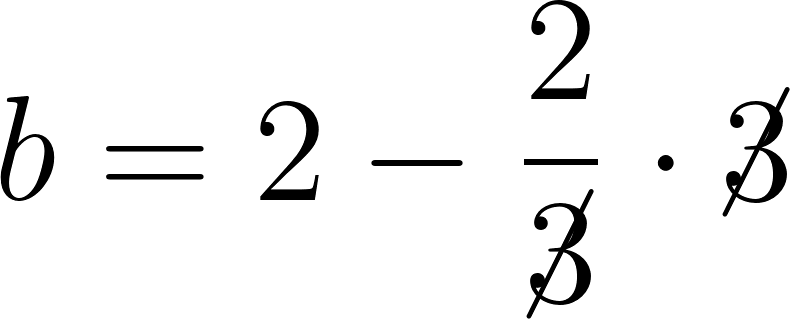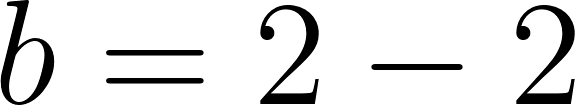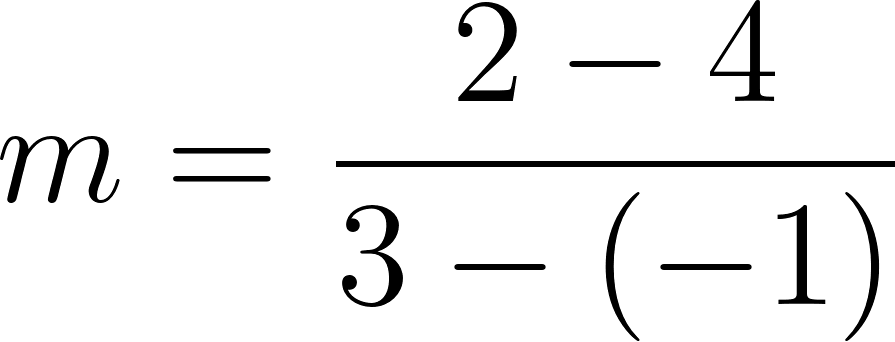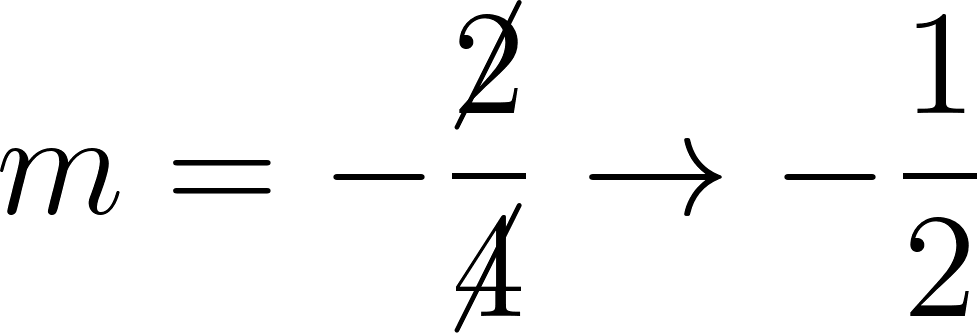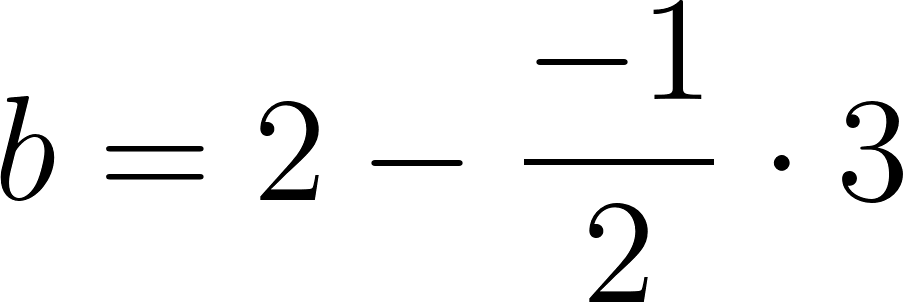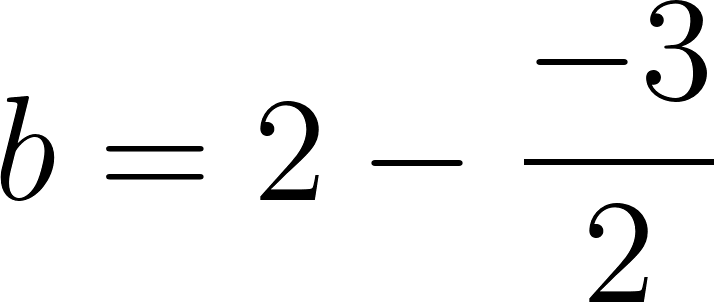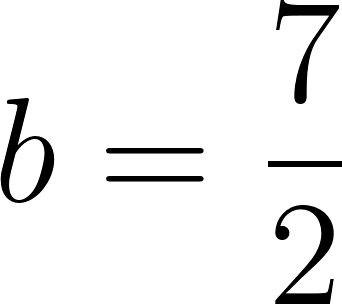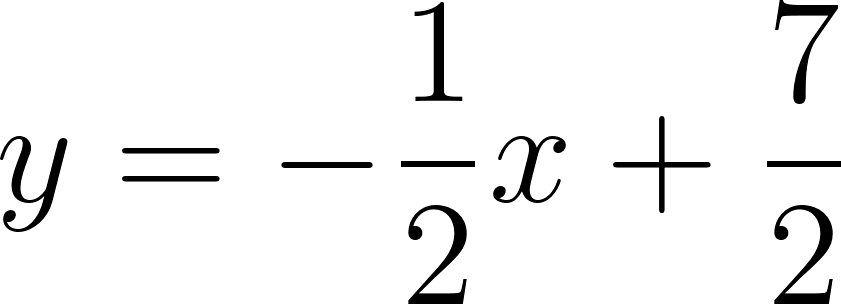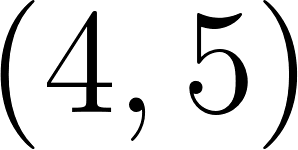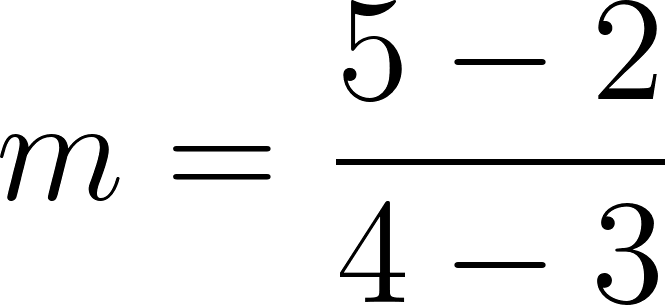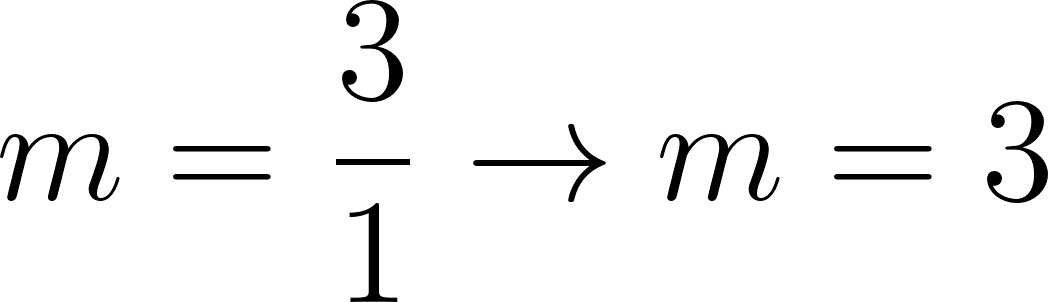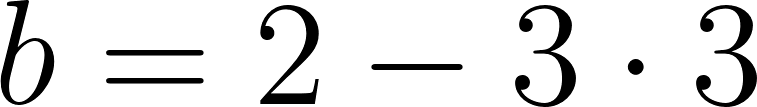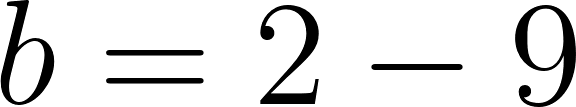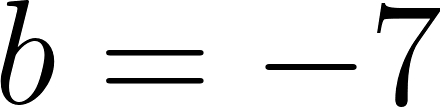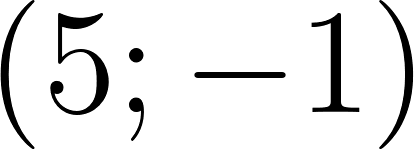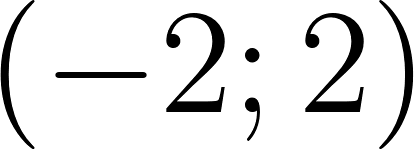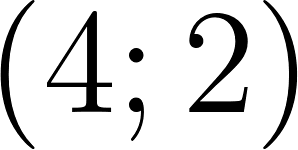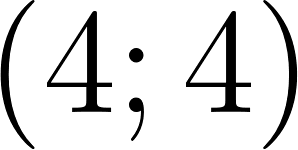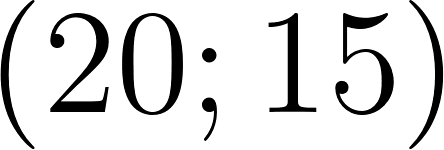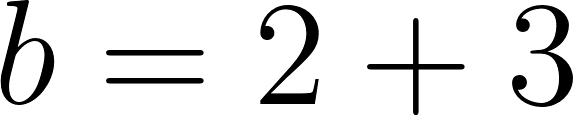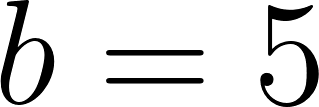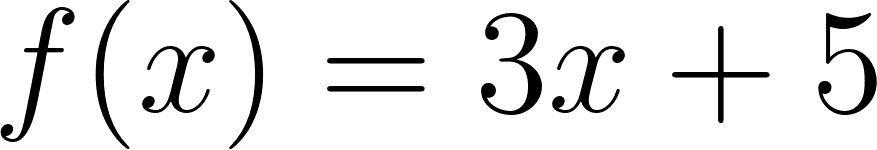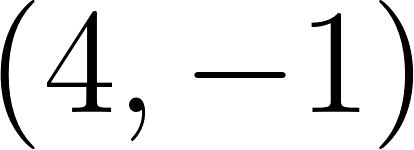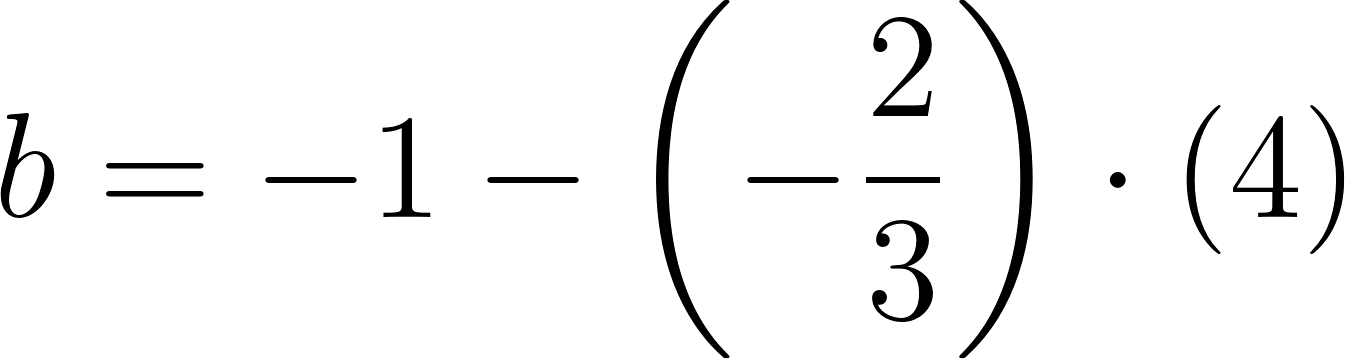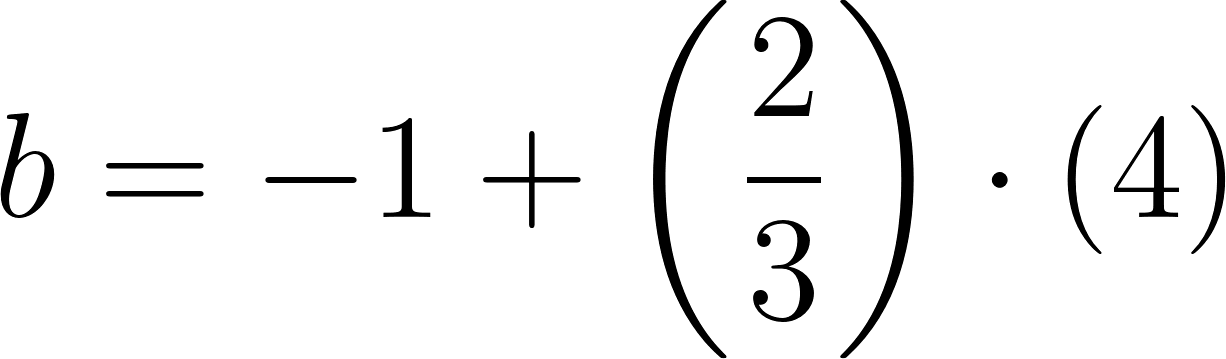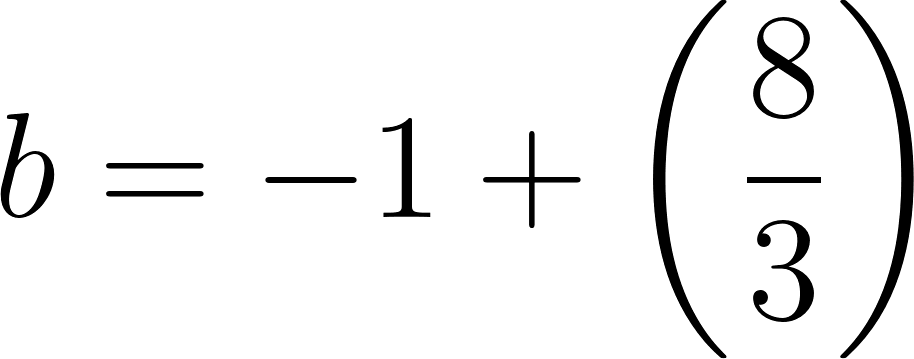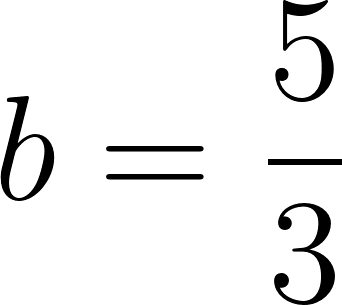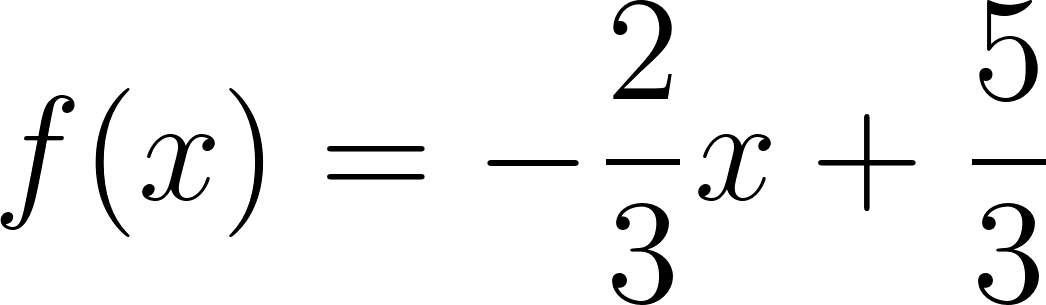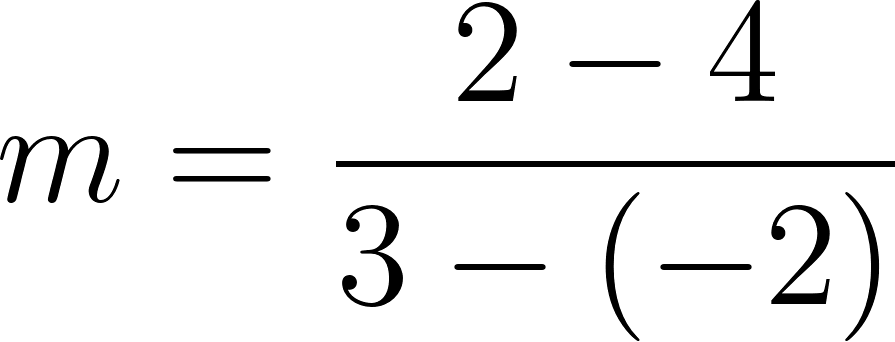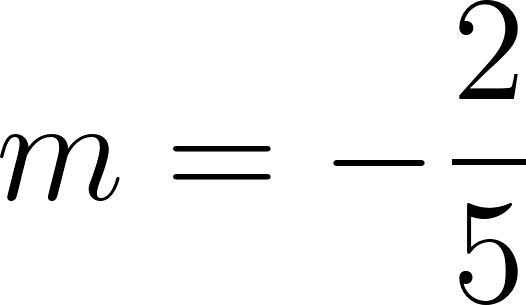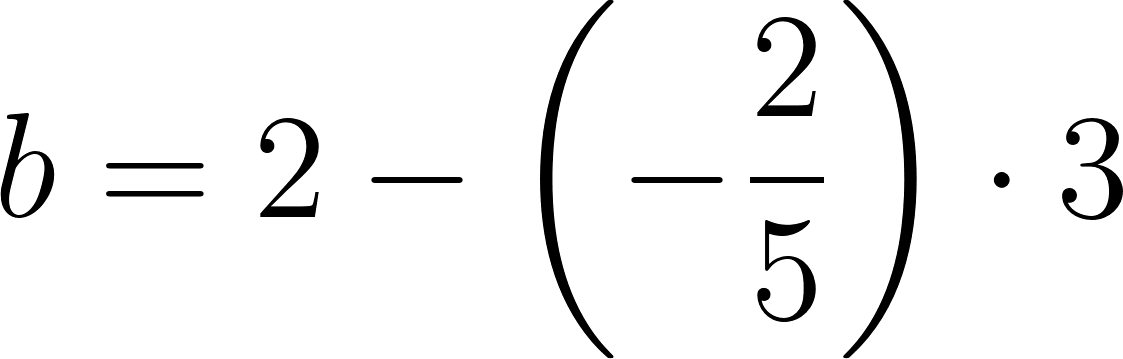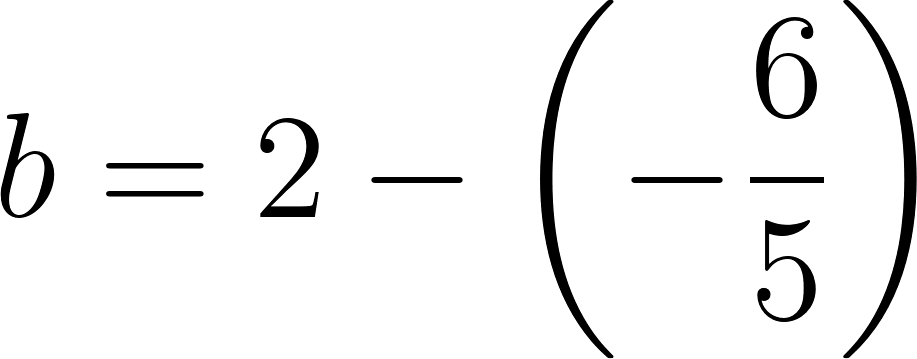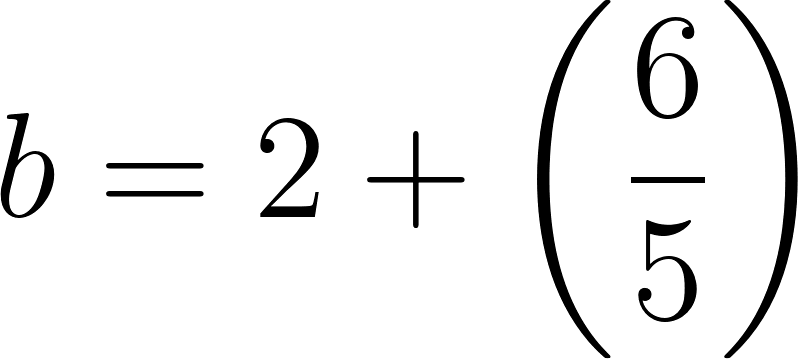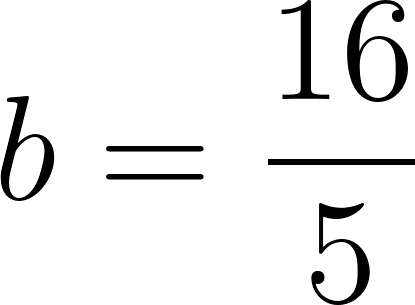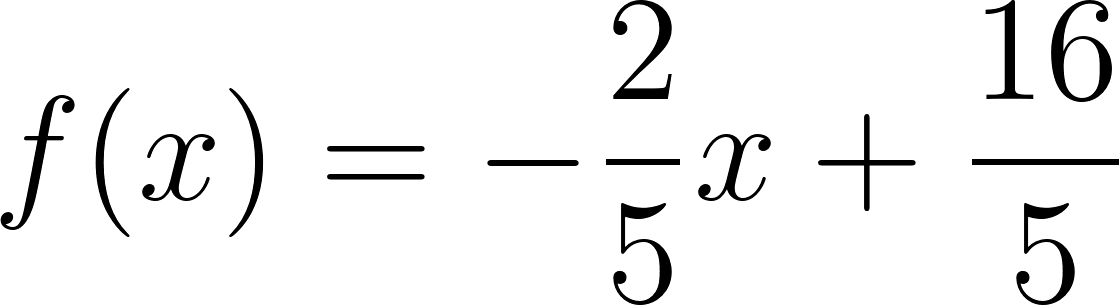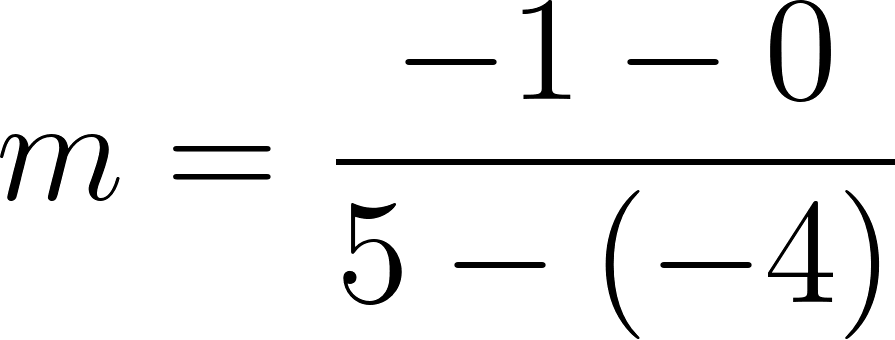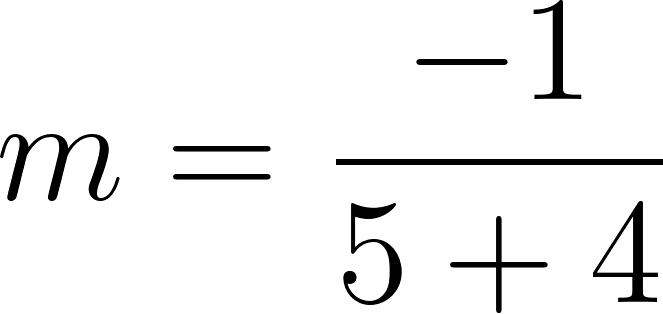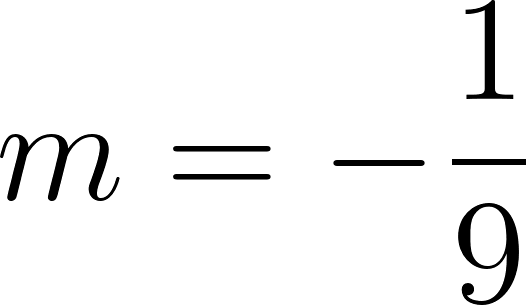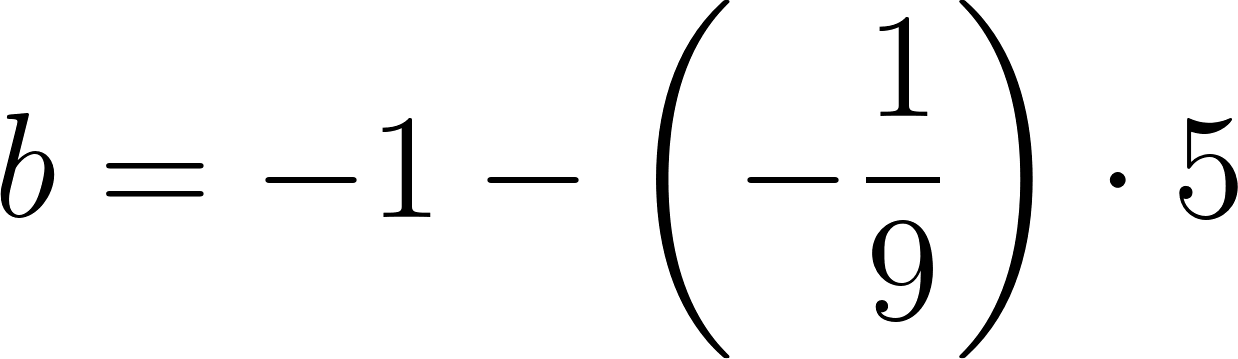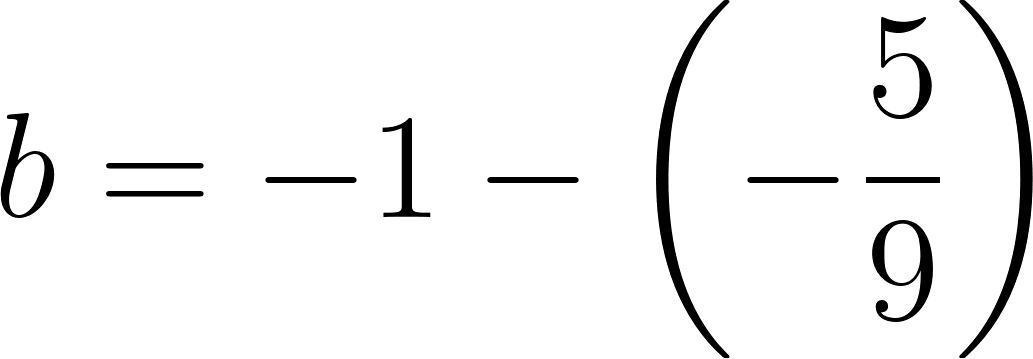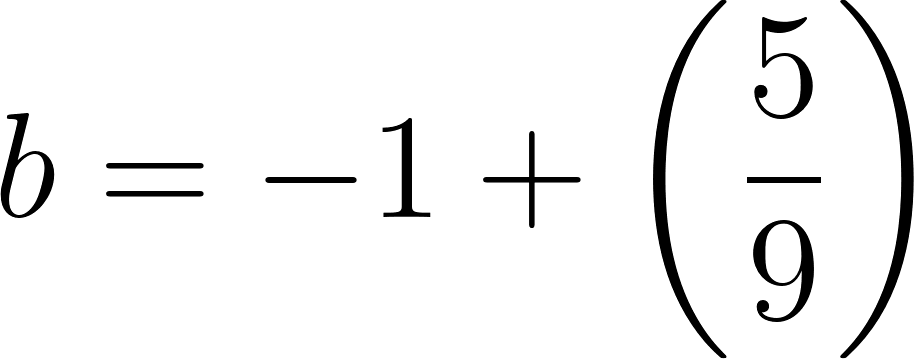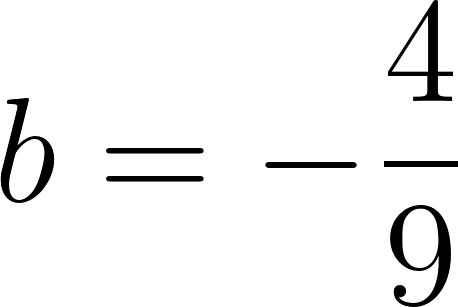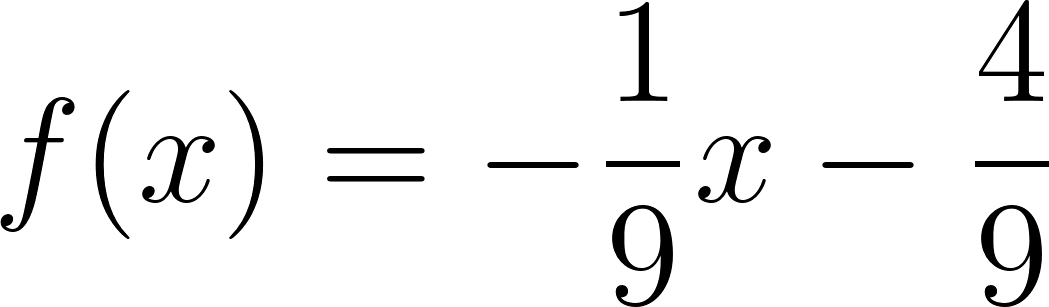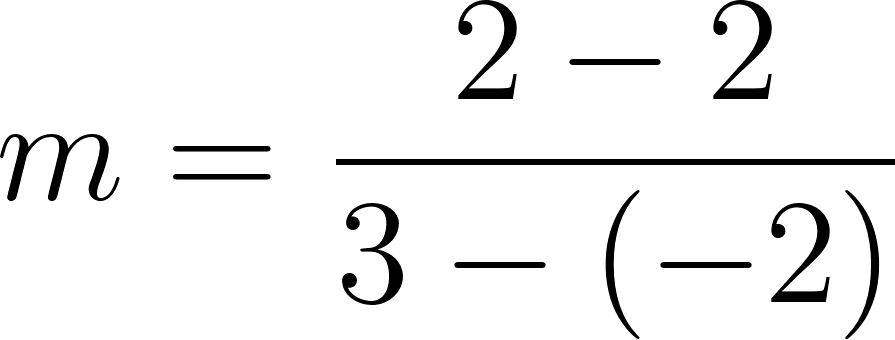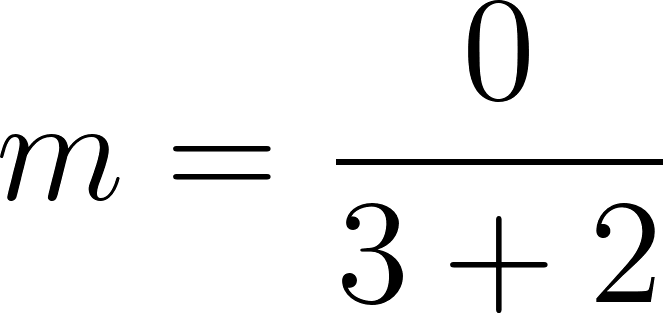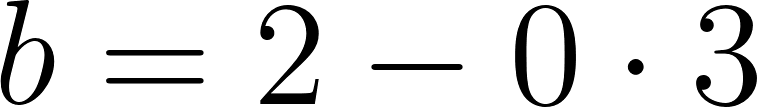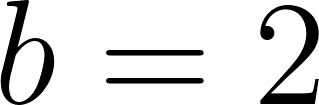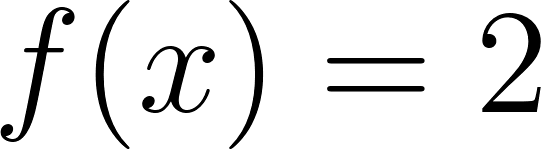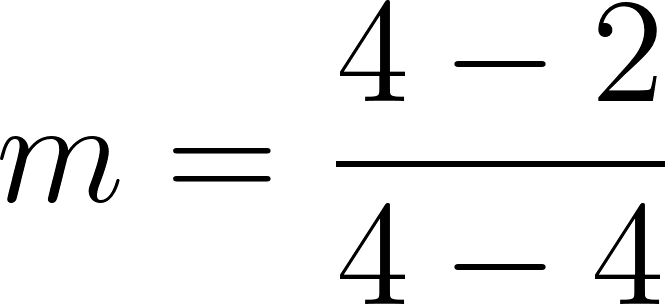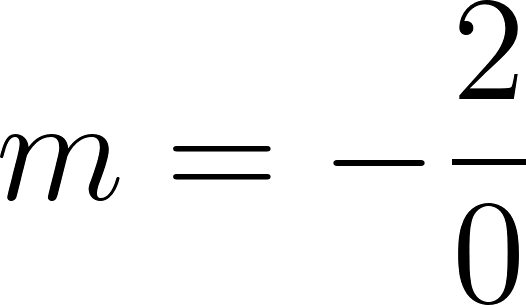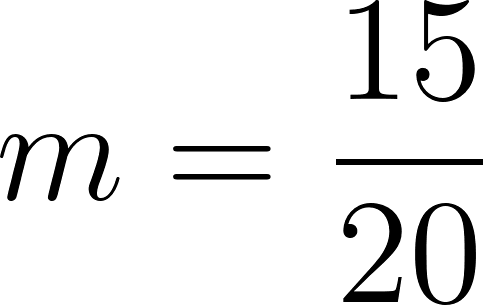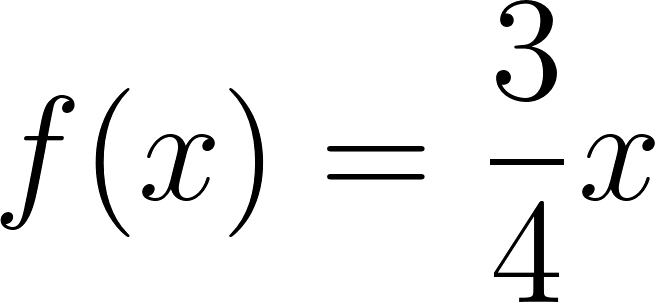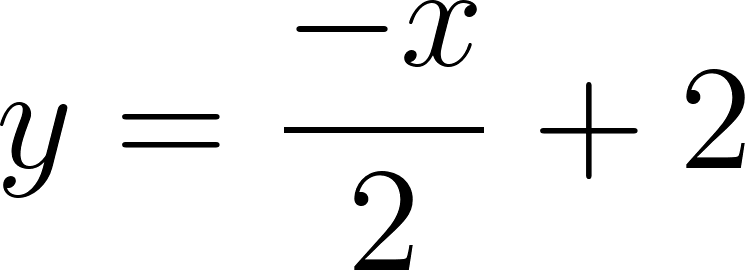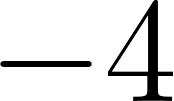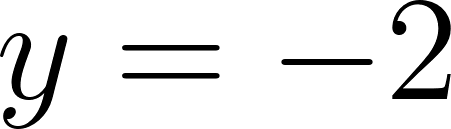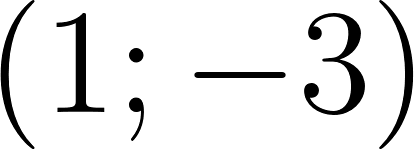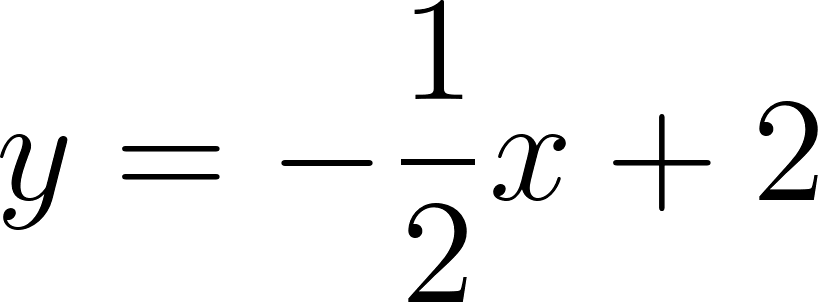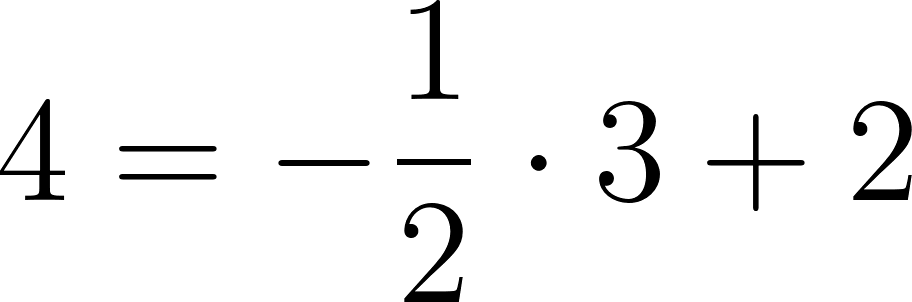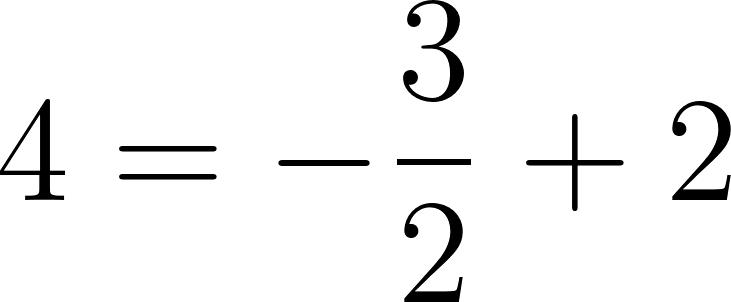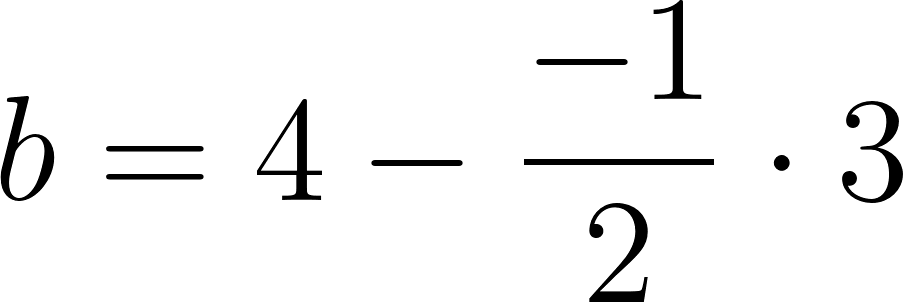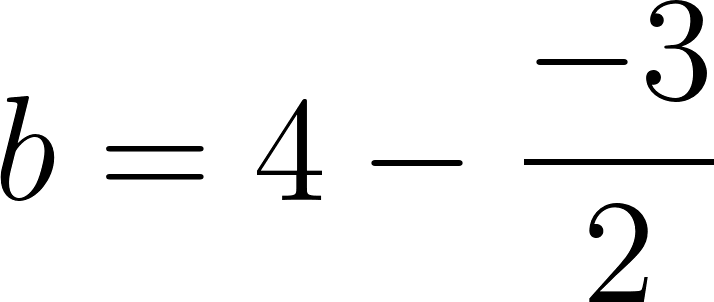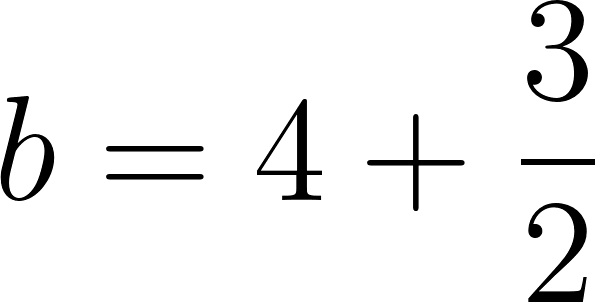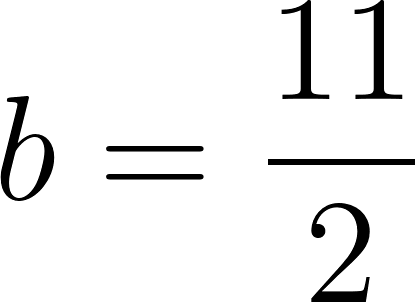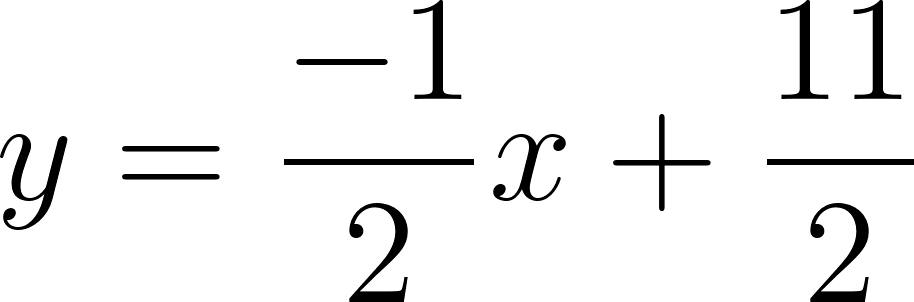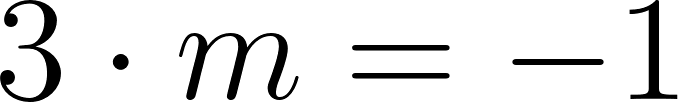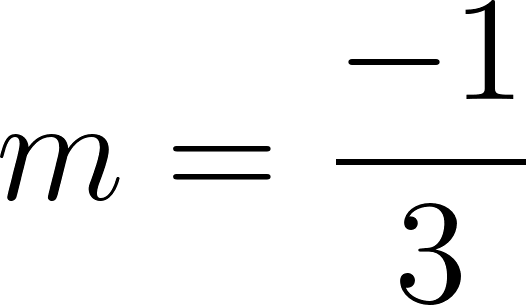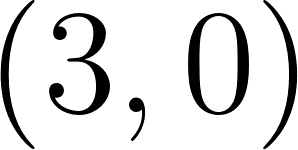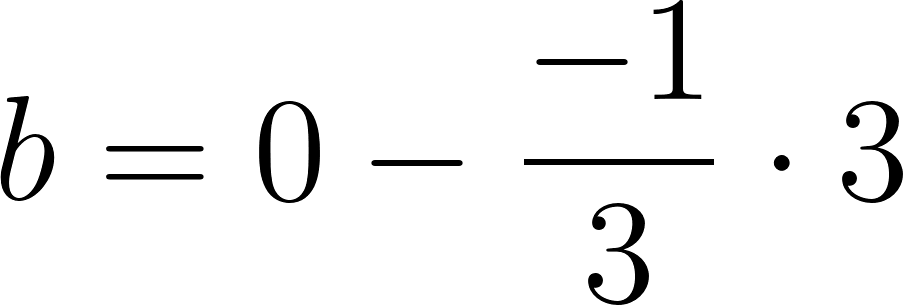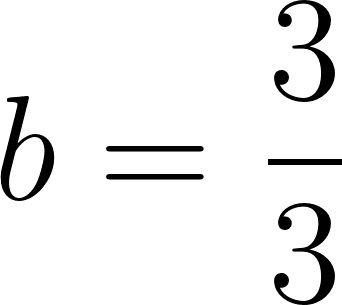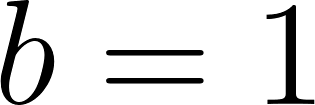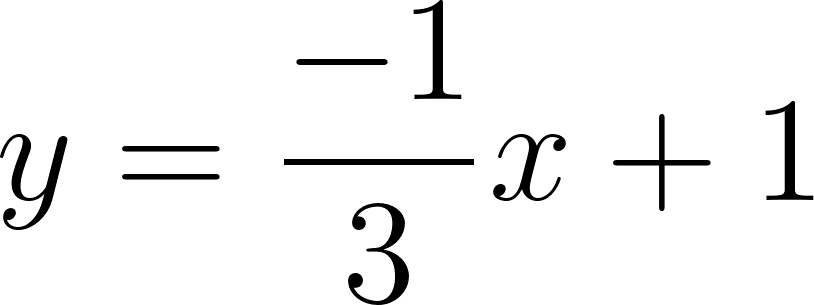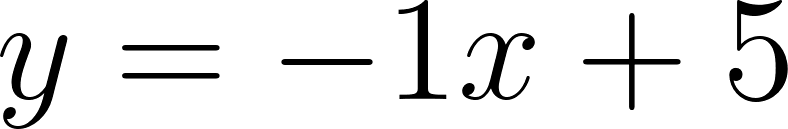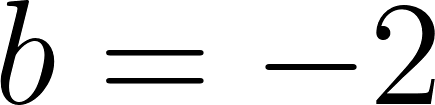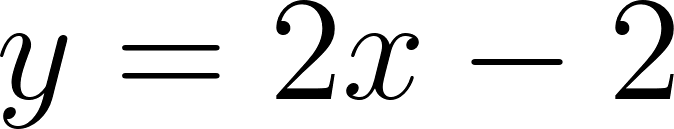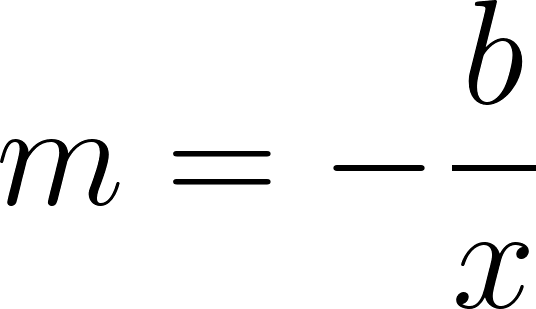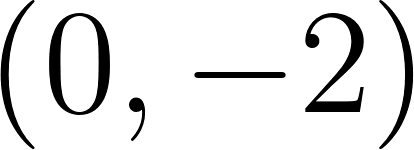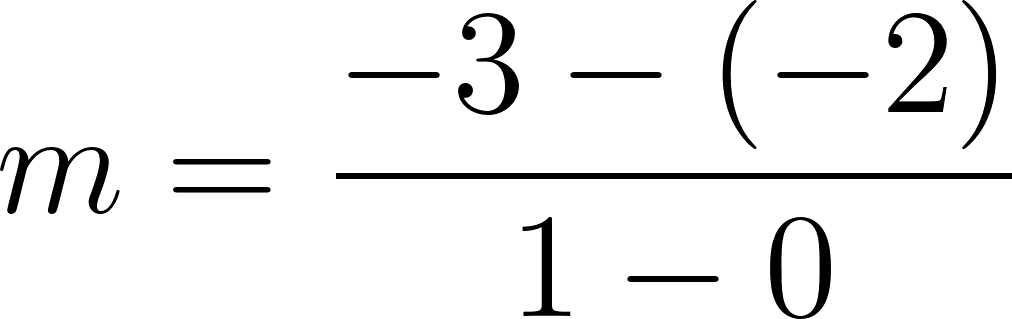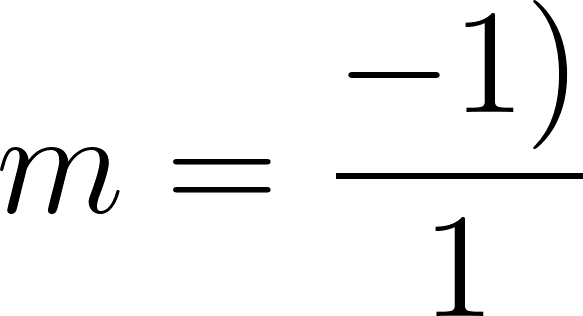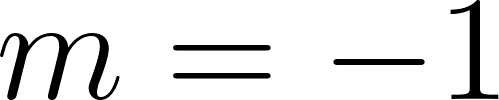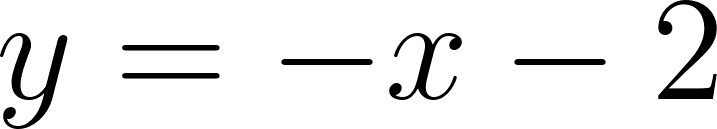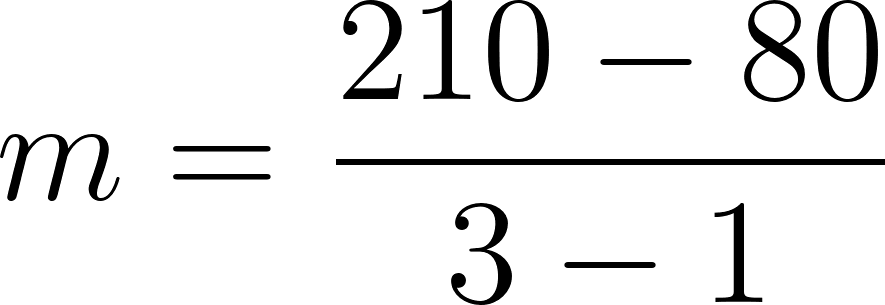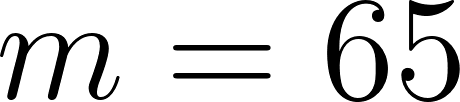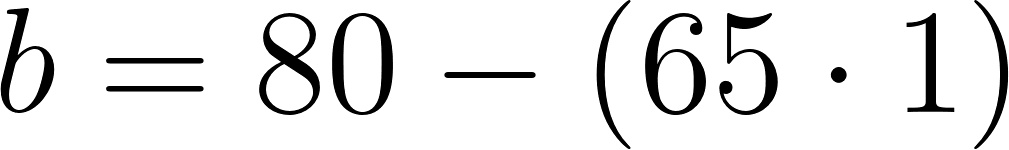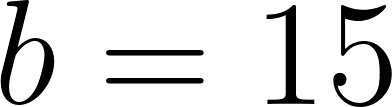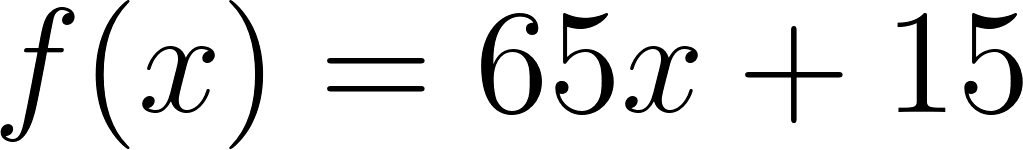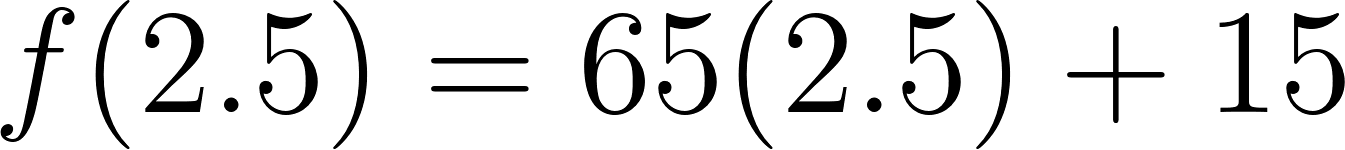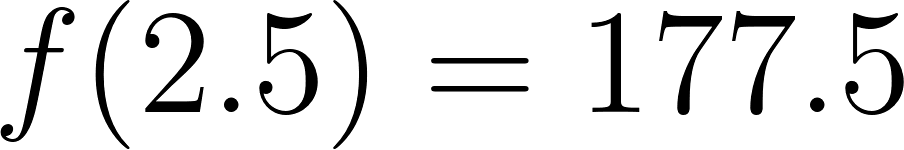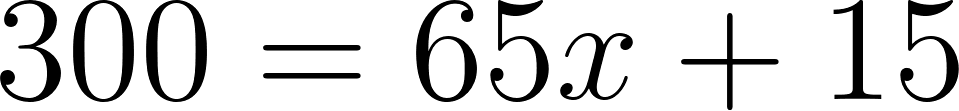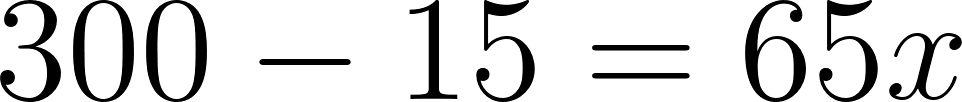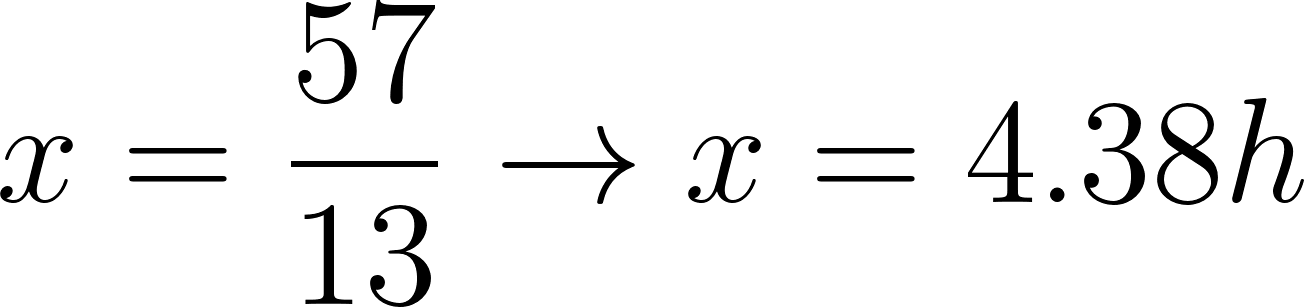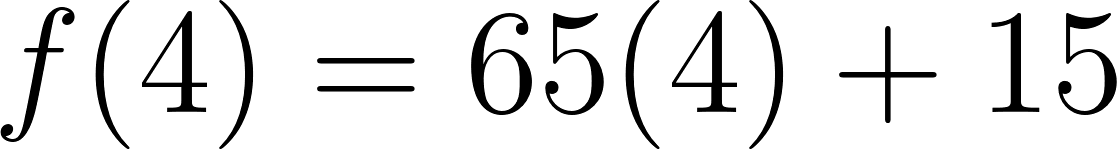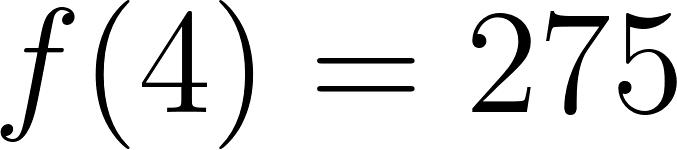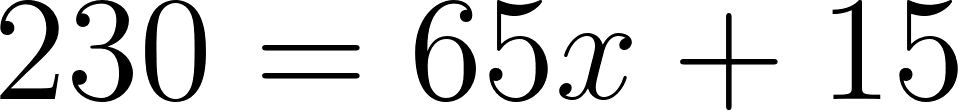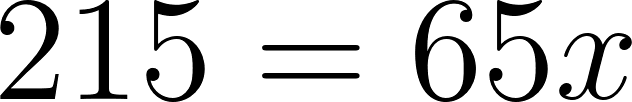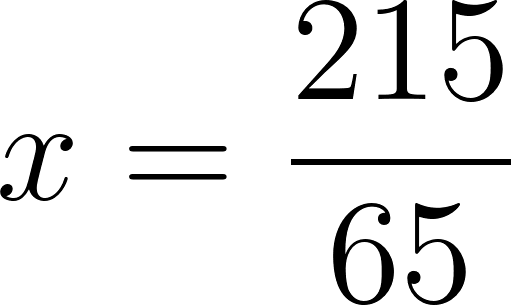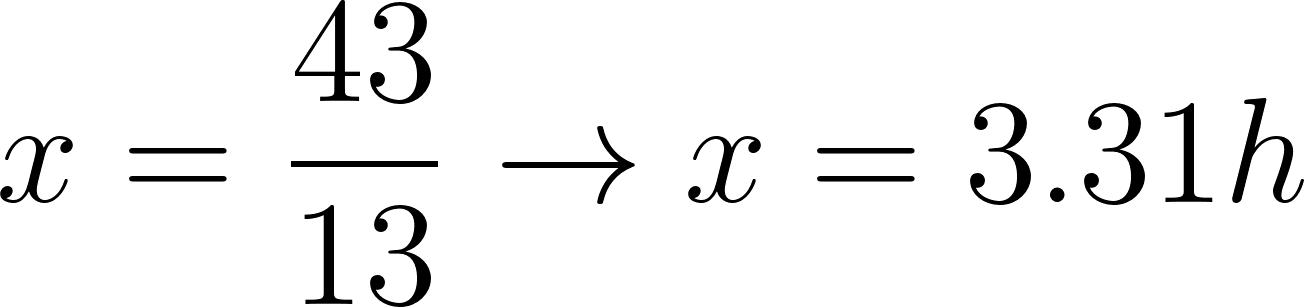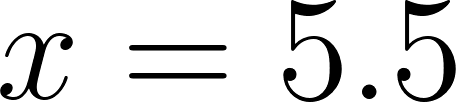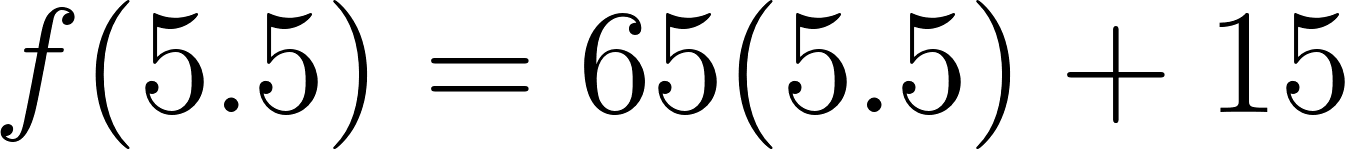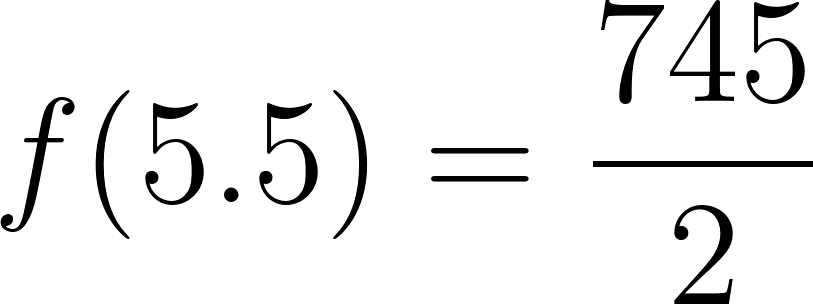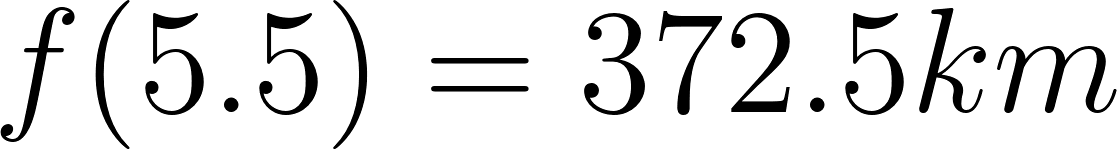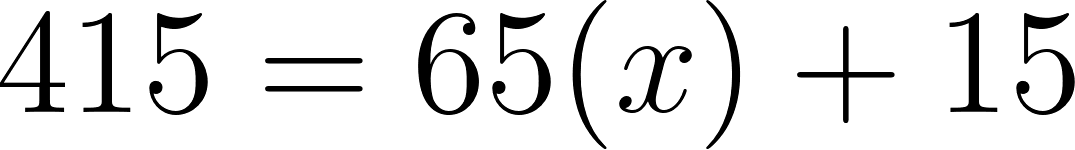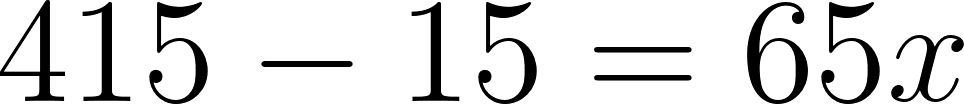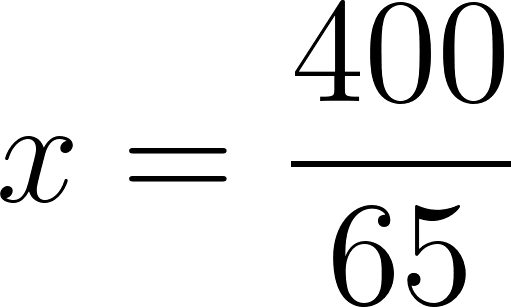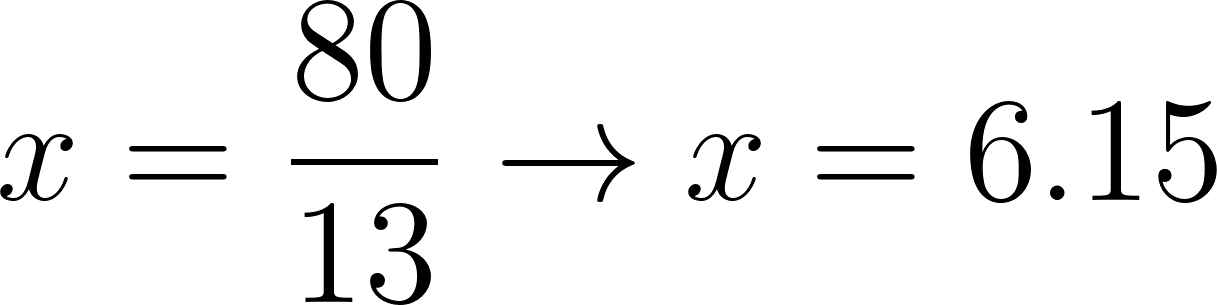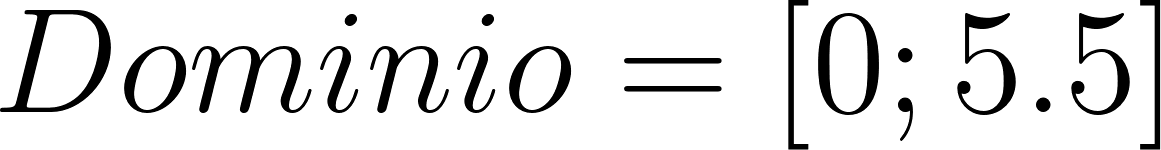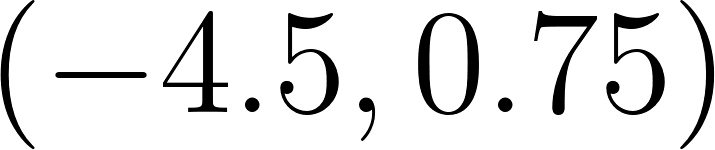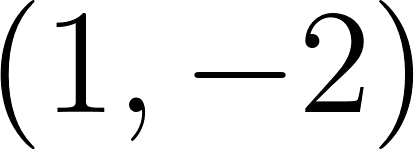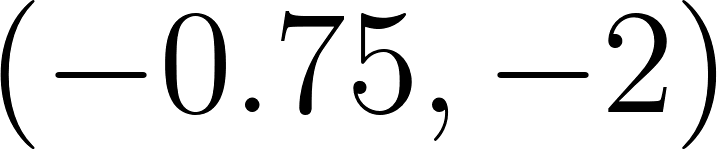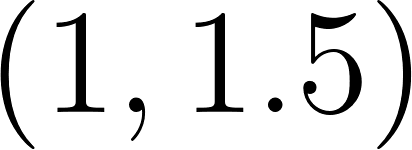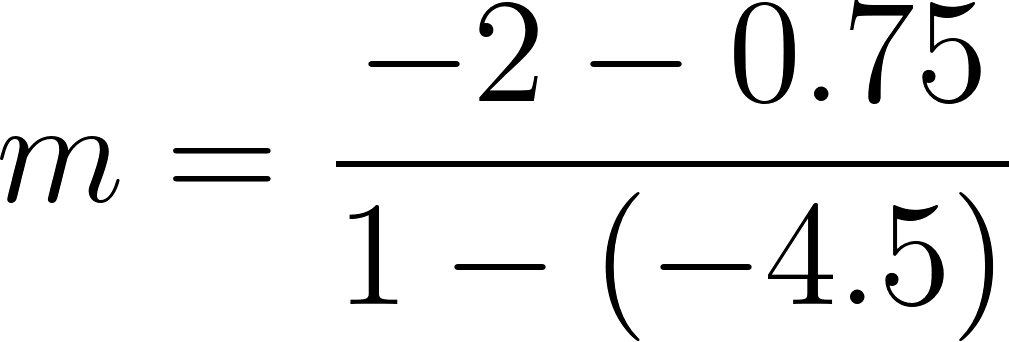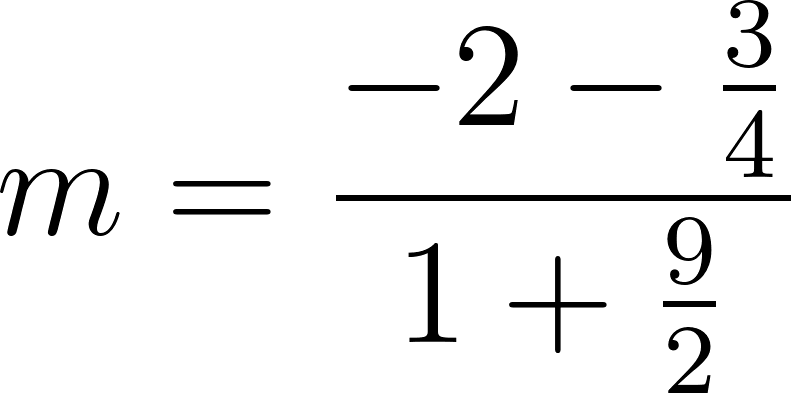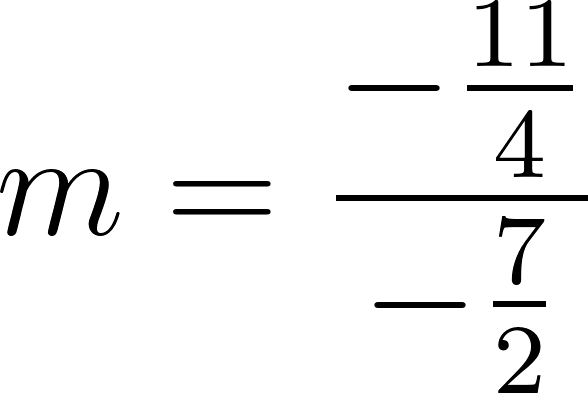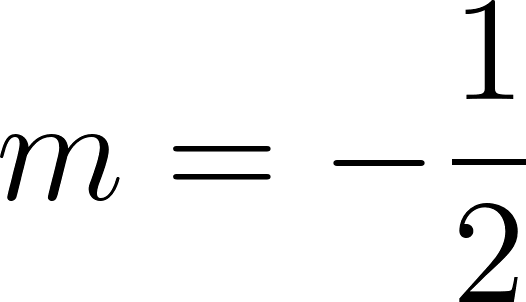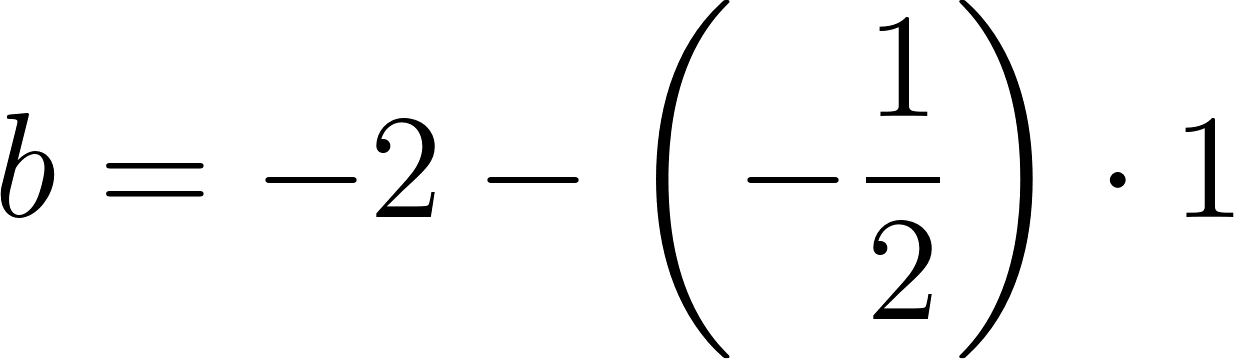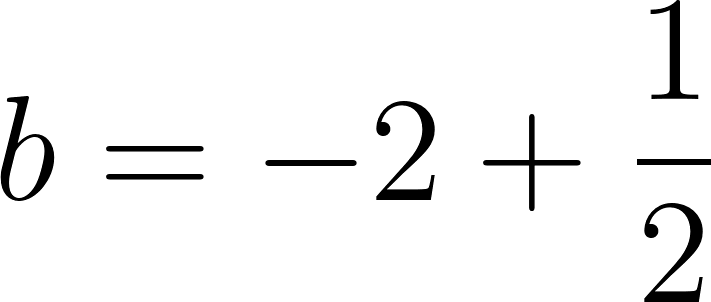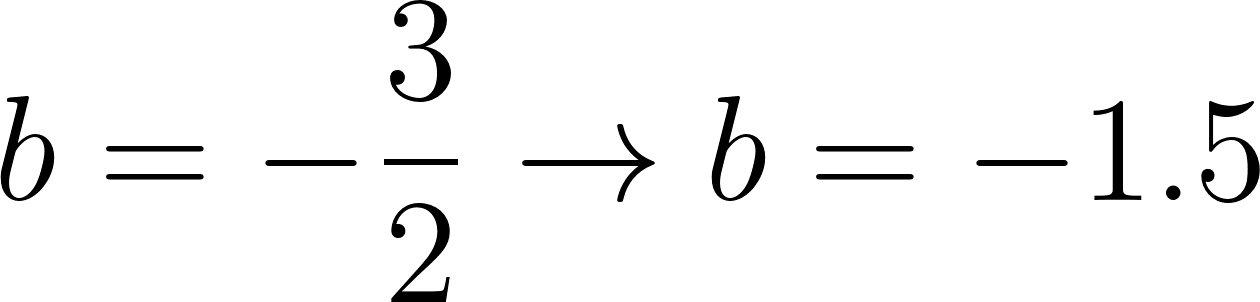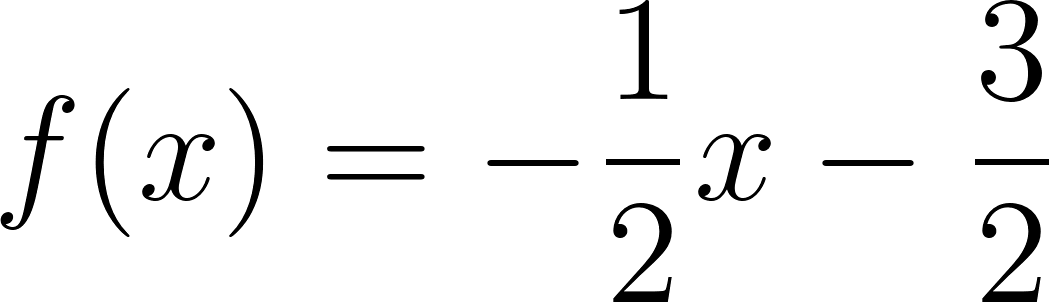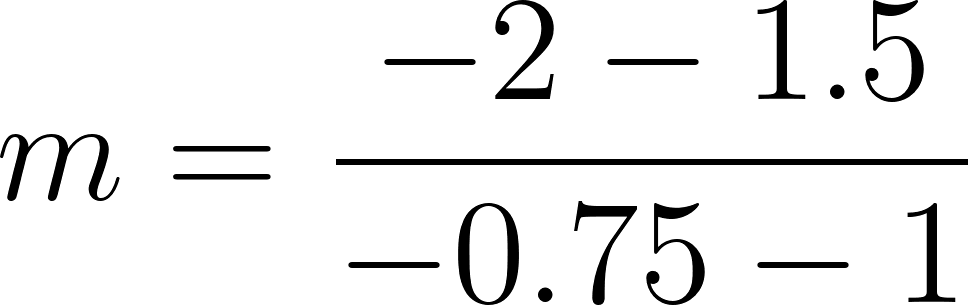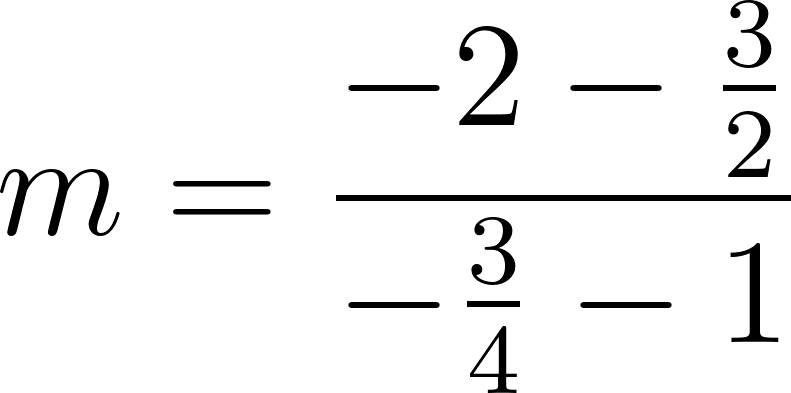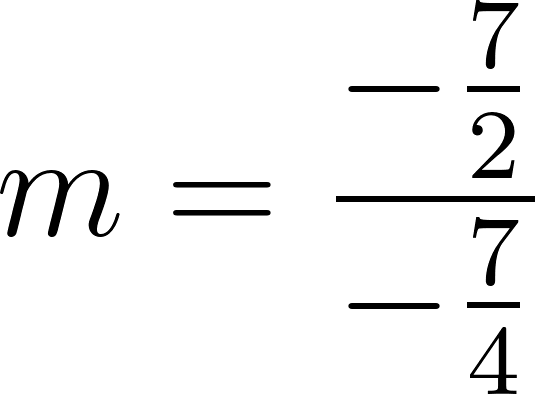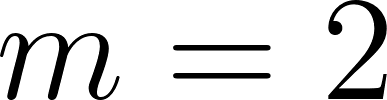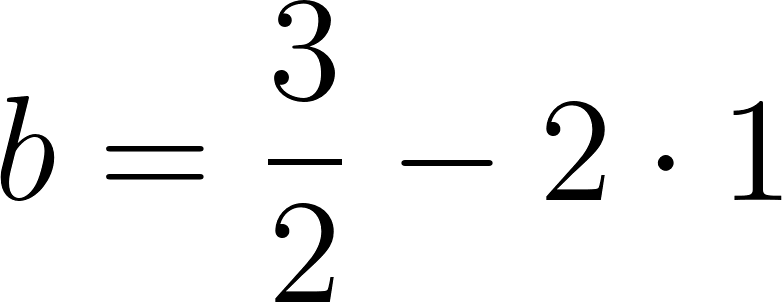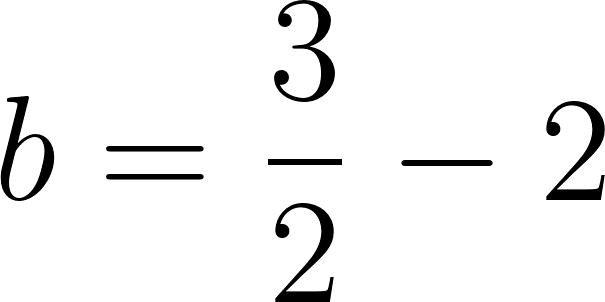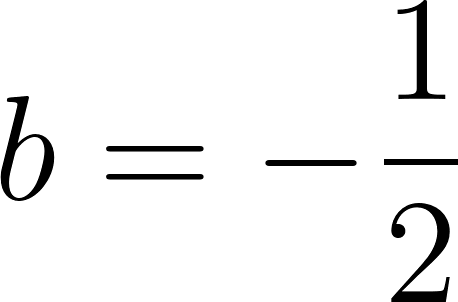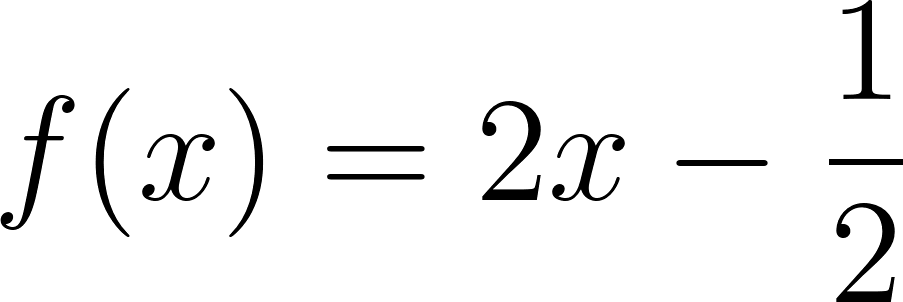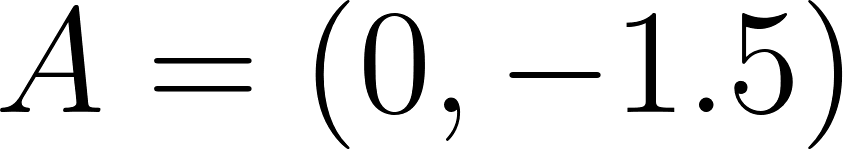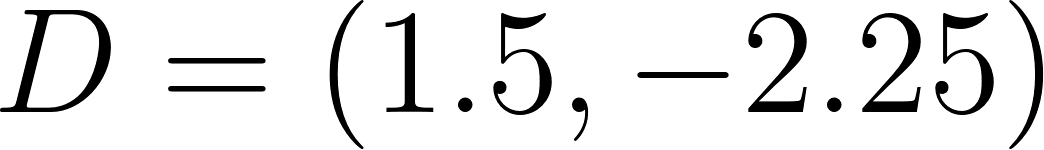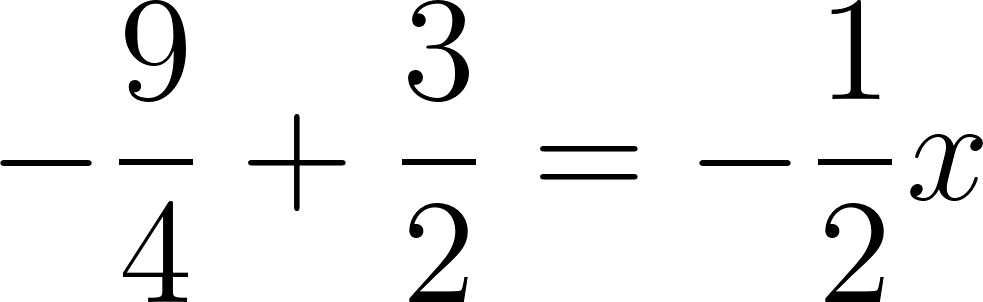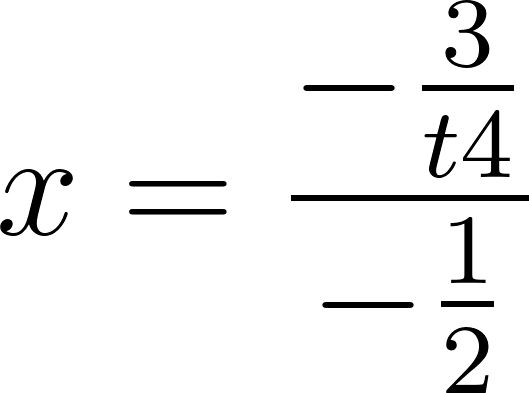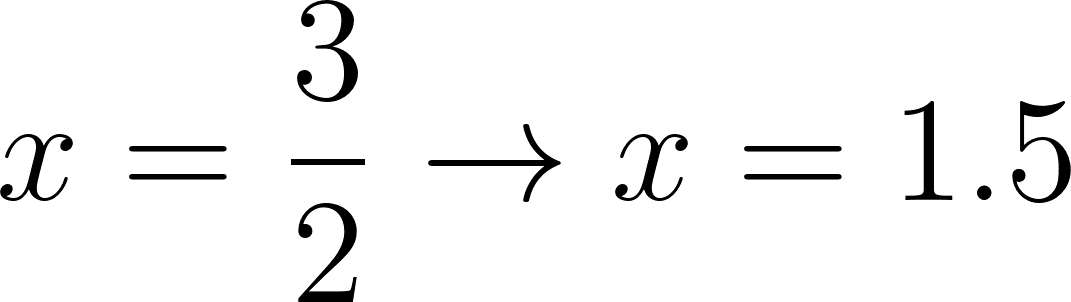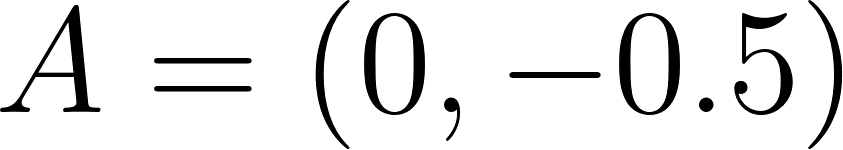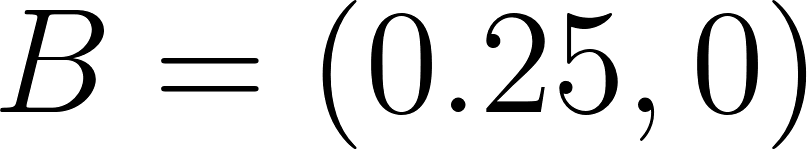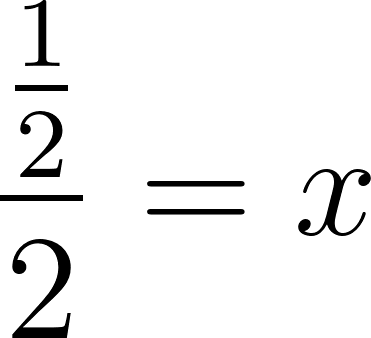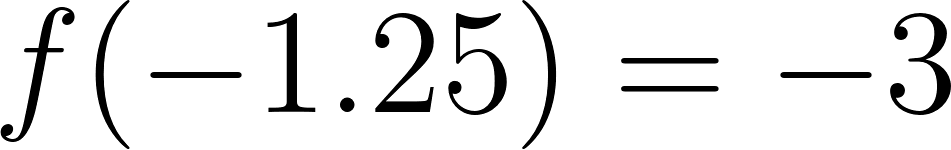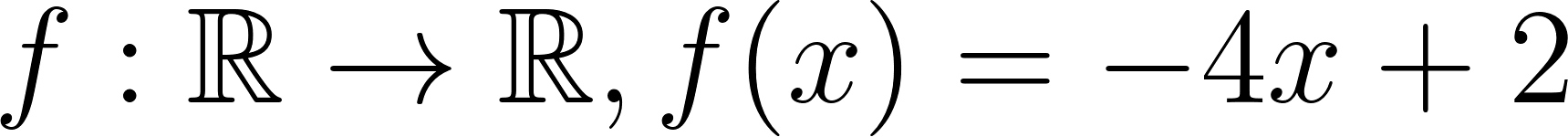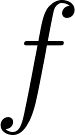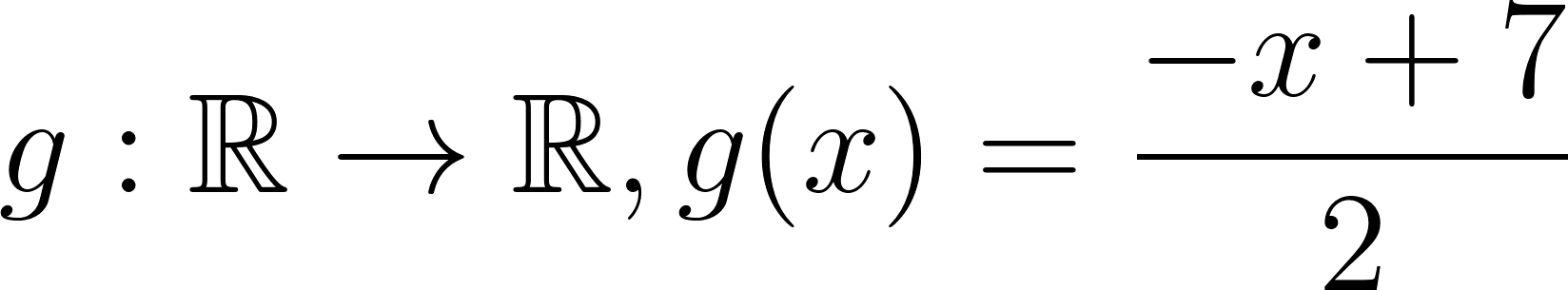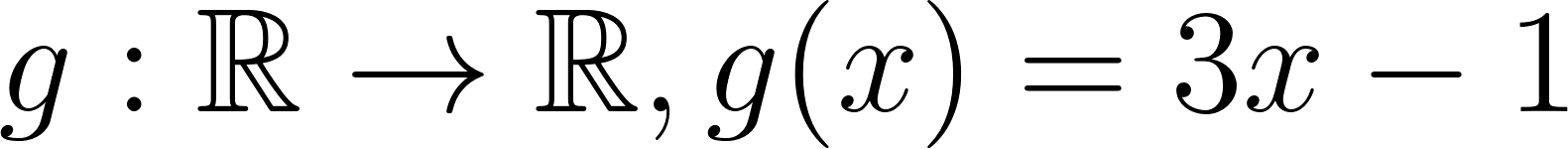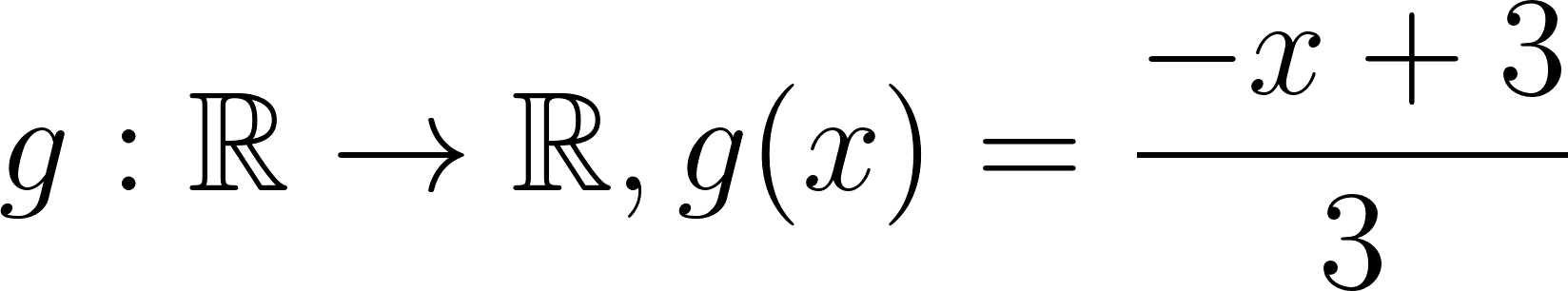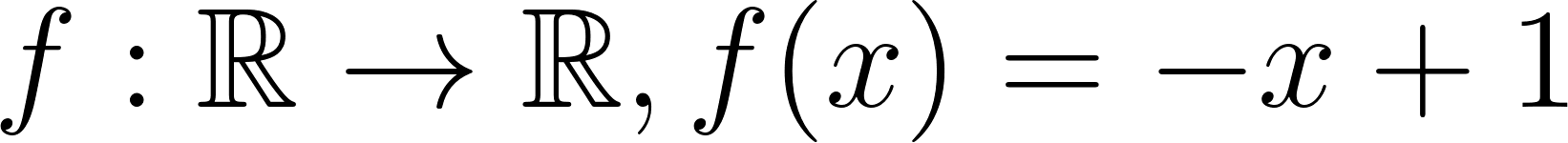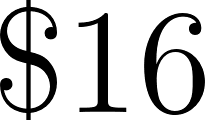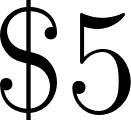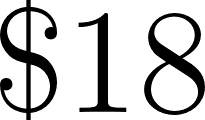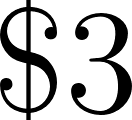Unidad 2

Función Lineal

01: Para empezar

• Lean el problema 1 de la Unidad 2, que se encuentra en la guía de problemas.
• Anoten los datos, intenten resolverlo, escriban lo que no entienden.
• Luego aborden el problema 2 (¡¡atención!! es una continuación del problema 1).
• Luego miren el video donde Gonzalo resuelve ambos problemas (¡OJO! tienen otra numeración porque también son utilizados en la guía de Matemática para Cs. Económicas)

• Problema 1 y 2 con GeoGebra

Problema 1:

Un auto sale de una ciudad que está sobre la Ruta Nacional 2, entre Buenos Aires y Mar del Plata. En la siguiente tabla se informa sobre la distancia a la que se encuentra de Buenos Aires en distintos momentos de su viaje. Se supone que el auto viaja siempre a la misma velocidad.

1. ¿Es cierto que a las tres horas de salir está a 320 km de Buenos Aires?
2. ¿A qué distancia de Buenos Aires estará a las tres horas y media de haber salido?.
3. ¿A qué distancia de Buenos Aires se encuentra la ciudad de donde partió?
4. Realicen un gráfico que represente la distancia del auto a Buenos Aires a medida que transcurre el tiempo de viaje. Agreguen al gráfico cartelitos con anotaciones para explicar la información importante que se puede observar en distintas partes.
5. ¿A qué velocidad viaja el auto?
6. Propongan una fórmula que permita calcular la distancia del auto a Buenos Aires en función del tiempo transcurrido.

Problema 2:

 Volviendo al Problema 1 respondan:

1. Otro auto parte desde otra ciudad que está en la ruta entre Buenos Aires y Mar del Plata, ubicada a 10 km de Buenos Aires. Este auto también viaja siempre a la misma velocidad: 120 km/h. ¿Se van a cruzar estos dos vehículos? En caso afirmativo, ¿en dónde y en qué momento?
2. Si este último auto hubiese partido a una velocidad de 95 km/h, ¿se habría cruzado con el primero? En caso afirmativo, ¿en dónde y en qué momento?
3. Realicen, en un mismo sistema de ejes, tres gráficos de manera que cada uno represente la distancia de cada uno de los autos a Buenos Aires en función del tiempo.

Resolución Problema 1:

Por lo tanto:

         es lo mismo que:

o:

Siendo una función lineal:

         Podemos averiguar la ordenada al origen

         Para saber en qué posición estaba al salir o iniciar su recorrido, usamos los datos de la tabla, conociendo que en 60 min avanza 90 km, restamos 90 km a la posición donde estaba a los 60 min, es decir 140 km, y como el tiempo es cero, nos queda que  será igual a .

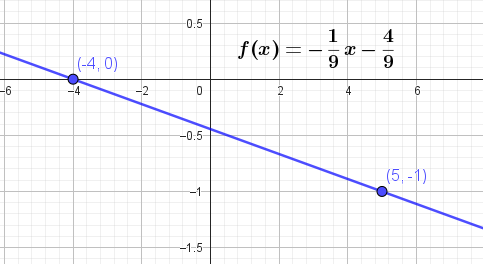
Con lo cual la función nos queda como:

         y como hablamos de tiempo, en lugar de  usamos , y en lugar de  usamos :

Una vez obtenida la función podemos calcular a qué distancia se encontrará a las tres horas:

Podemos responder afirmativamente a la pregunta, a las 3 horas de salir de Buenos Aires, se encontrará a 320km.

b) Para comodidad de los cálculos usaremos

        Siendo:

                 y suprimimos las unidades.

        Entonces a las tres horas y media se encontrará a:

        Se encuentra a 365 km de Buenos Aires.

c) Cuando partió se encontraba a 50 km de Buenos Aires.

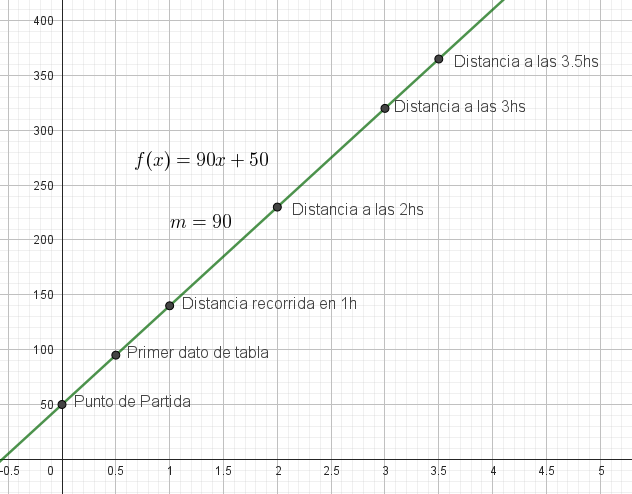
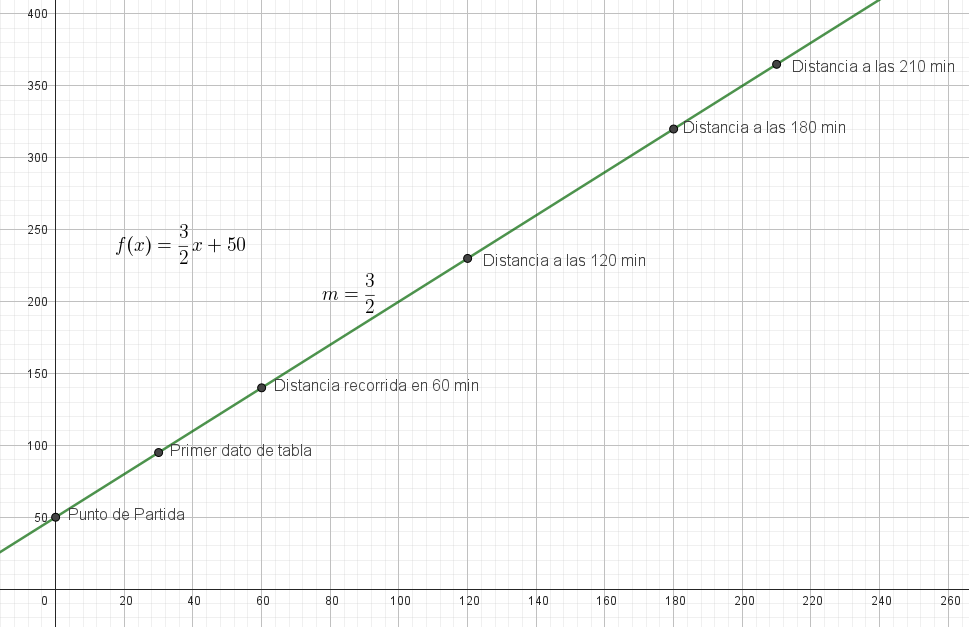
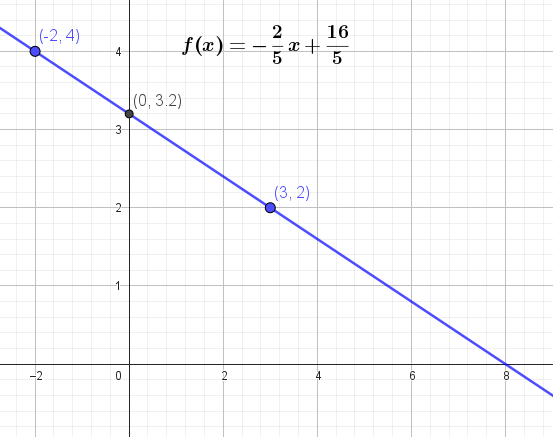
4. Gráficos en horas y minutos:

5. El auto viaja a razón de 90 km por cada hora recorrida.
6. Fórmula en minutos:

Fórmula en horas:

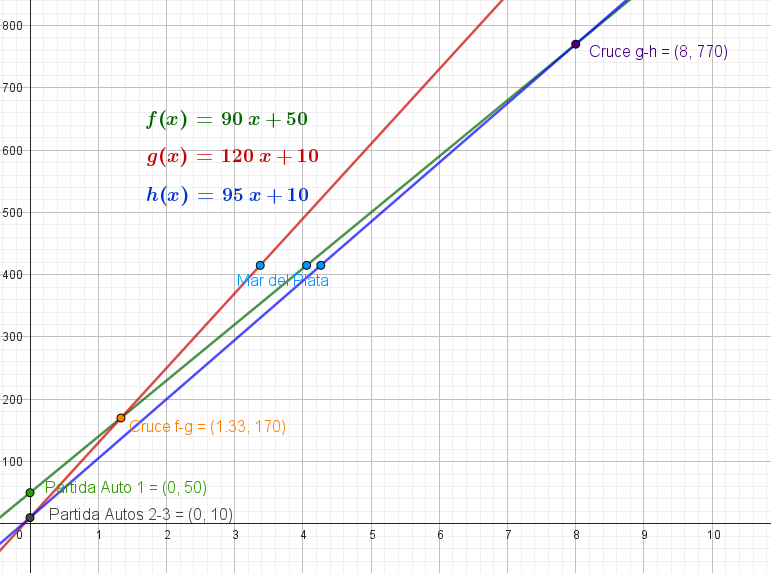
Resolución Problema 2:

1. Teniendo en cuenta que este automóvil viaja a una velocidad constante de  y parte de una ciudad a  de Buenos Aires, tenemos que:

Para evaluar si se cruzan, igualamos las ecuaciones para averiguar el momento en que se cruzan, si es que se cruzan.

         Igualamos a cero

         Despejamos t

Estos vehículos se cruzaron aproximadamente pasada una hora  evaluamos alguna de las dos funciones en t.

         o

         o

Con lo cuál se cruzan a los 170km pasada una hora desde que partieron.

2. Si este segundo vehículo hubiese tenido una velocidad constante de  su función es:

Igualamos ambas ecuaciones:

Igualamos a cero:

Evaluamos en t = 8h:

         o

         o

Los autos se cruzan a 770 km de Buenos Aires, pero su destino es Mar del Plata, que se encuentra a 415 km, por lo tanto no se cruzaran jamás, antes ambos llegaron a su destino.

3. Graficamos los tres casos:

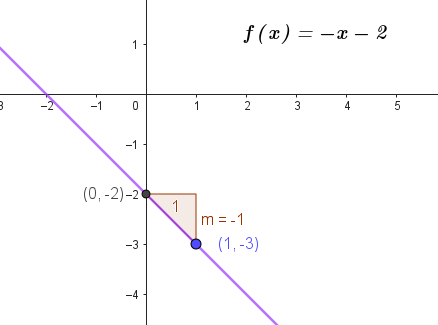
02: ¿Qué es la pendiente de la recta?

Problema 1 Pendiente de la recta en video

• Problema 1 Pendiente de la Recta

03: ¡A Trabajar!

¡A TRABAJAR!

Les proponemos reunirse en grupos y resolver los problemas 3, 4 y 5 de la guía de problemas.

• Anoten los datos del Problema.
• Ayudense con GeoGebra.
• Coloque bien las respuestas, en forma ordenada y precisa.

Problema 3: 

Roberto está por hacer un viaje y está averiguando para alquilar un auto. Averiguó en dos compañías:

• La compañía A le cobra $800 fijos y $1,10 por kilómetro recorrido.
• La compañía B le cobra $150 fijos y $1,35 por cada kilómetro recorrido.

1. Si estima que va a recorrer 1000 Km, ¿qué compañía le conviene contratar? ¿Y si recorriera 5000 Km?
2. Armen una fórmula correspondiente a la compañía A y otra correspondiente a la compañía B, que represente el costo del alquiler en función de los kilómetros recorridos. ¿A partir de qué kilometraje le conviene cada compañía?
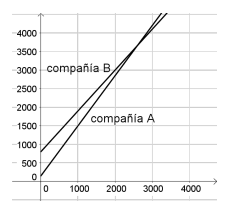
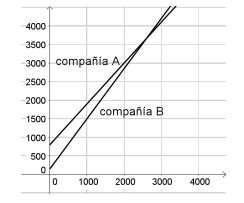
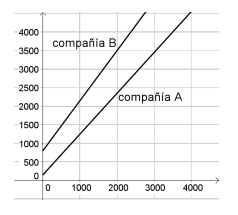
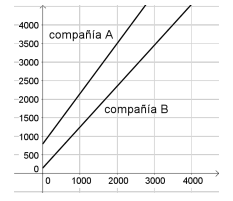
3. ¿Cuáles de estos gráficos sirven para representar la situación?:

4. Si finalmente Roberto eligió la compañía A y cuando terminó el viaje el costo del alquiler fue de $3355,30, ¿cuántos kilómetros recorrió?

Resolución Problema 3:

        Compañía A:

        Compañía B:

1. En la compañía A:

Caso 1:

Caso 2:

2.  En la compañía B:

Caso 1:

Caso 2:

Para recorrer 1000 km le conviene la compañía B. En cambio, si va a recorrer 5000 km le conviene la compañía A.

2. Fórmulas:

1. Compañía A:

2. Compañía B:

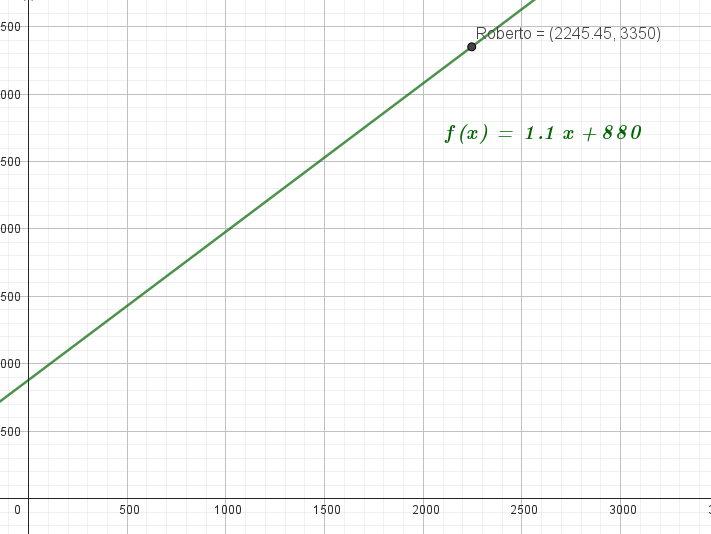
3. Gráfico 2.
4. Si  entonces:

 Roberto recorrió 2245,45 km aproximadamente.

Problema 4:

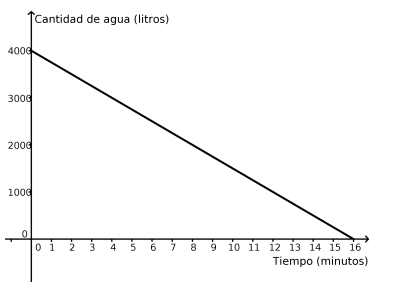
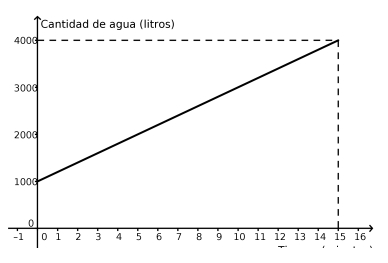
        El gráfico representa el proceso de vaciado de un tanque de agua.

1.  ¿Qué cantidad de agua tenía el tanque cuando empezó a vaciarse?
2. ¿Cuánto tardó en vaciarse?
3.  ¿Cuántos litros por minuto salían del tanque mientras se vaciaba?
4. Marquen sobre el gráfico el punto que representa el momento en que el tanque tenía 3000 litros. ¿Cuánto tiempo había transcurrido desde que comenzó a vaciarse?
5. Escriban una fórmula que calcule la cantidad de agua que había en el tanque a los  minutos de haber comenzado a vaciarse.

Resolución Problema 4:

1. El tanque tenía 4000 litros de agua.
2. Tardó en vaciarse 16 minutos
3. Salían 250 litros por minuto:

4. Siendo la función:

         Transcurrieron 4 minutos desde que comenzó a vaciarse

5. Fórmula:

Problema 5:

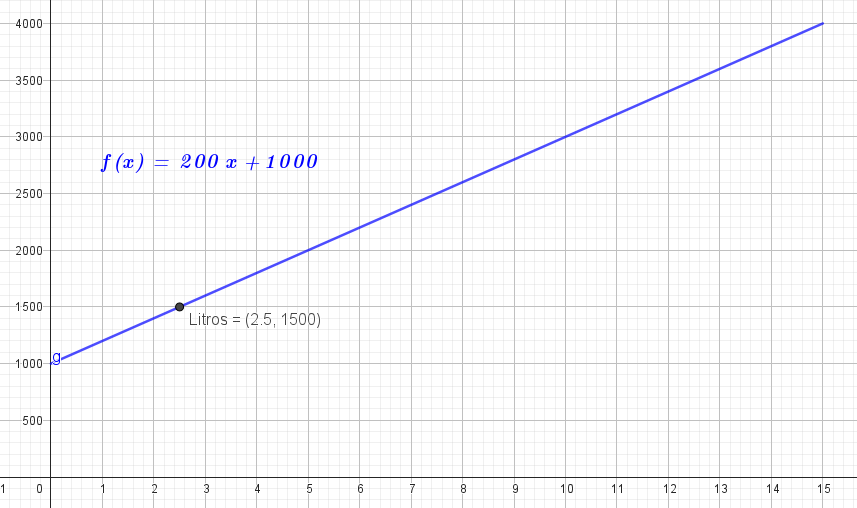
        El gráfico representa el proceso de llenado de un tanque de agua a partir del momento en que se abrió una canilla.

1.  ¿Qué cantidad de agua tenía el tanque cuando se abrió la canilla y empezó a llenarse?
2. ¿Cuántos litros por minuto entraron al tanque mientras se llenaba?
3. Marquen sobre el gráfico el punto que representa el momento en que el tanque tenía 1500 litros. ¿Cuánto tiempo había transcurrido desde que comenzó a llenarse?
4. Escriban una fórmula que calcule la cantidad de agua que había en el tanque a los  minutos de haber comenzado a llenarse.

Resolución Problema 5:

1. El tanque tenía 1000 litros de agua cuando se abrió la canilla.
2. Entraron 200 litros por minuto:

3. Siendo la función:

         Transcurrieron 2 minutos y medio desde que comenzó a llenarse.

4. Fórmula:

04: Ecuación de la recta:

Episodio 1:

Ecuación de la recta. Episodio I

Ecuación de la Recta: Episodio 1

Episodio 2:

Ecuación de la recta. Episodio II

Ecuación de la Recta: Episodio 2

05: Para Saber Más:

Para saber más

• Les dejamos el enlace a un apunte teórico que reúne todos los conceptos más importantes sobre función lineal.
• Además les dejamos algunas animaciones de GeoGebra:

• Animación 1
• Animación 2
• Animación 3

Para que investiguen, indaguen y utilicen como herramienta de ayuda en la resolución de los problemas.

Apunte teórico:

Función lineal

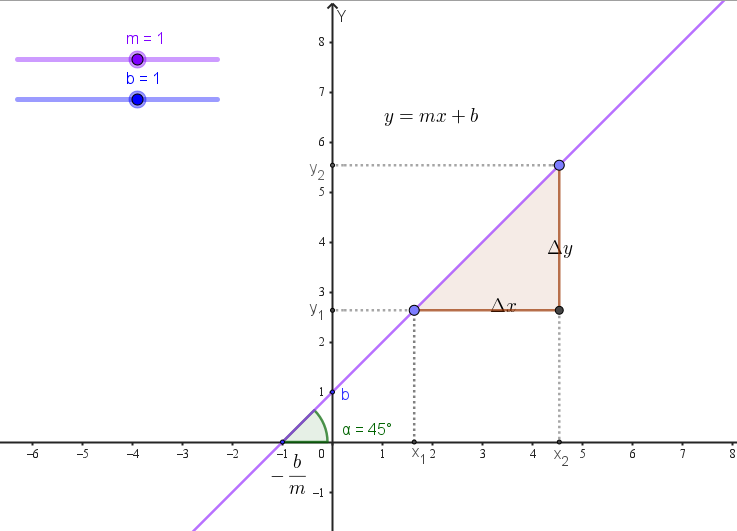
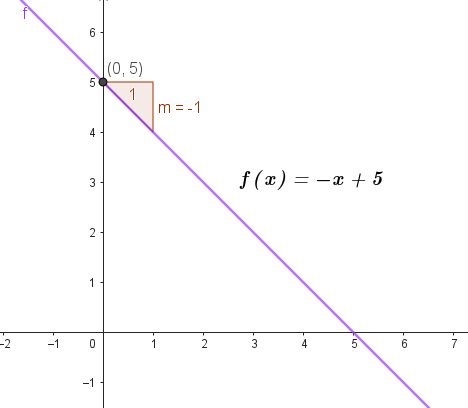
Decimos que una función es lineal si es de la forma  y algunas de sus características son:

• Su representación gráfica es una recta (que no es vertical, ya que las rectas verticales no representan funciones).

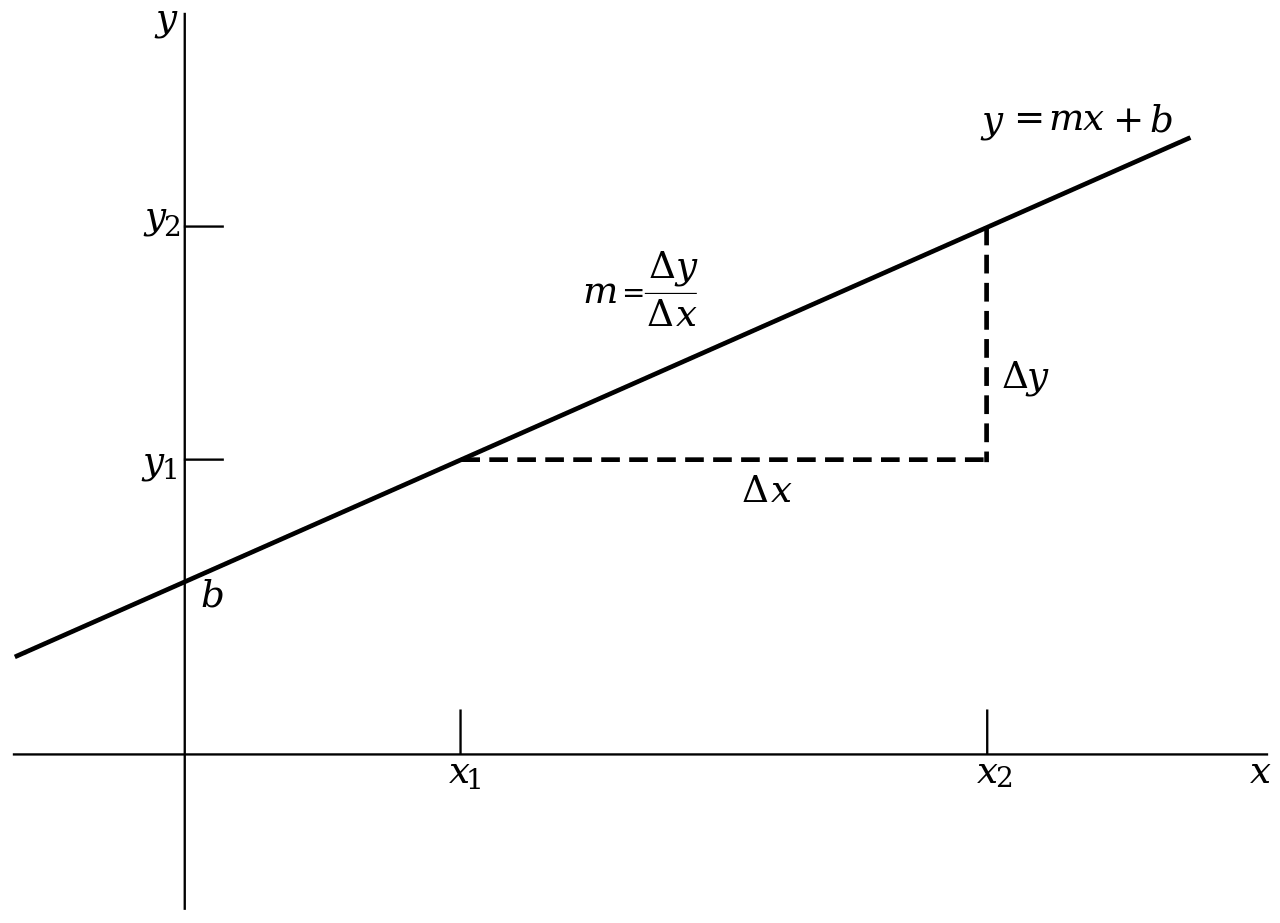
• Depende de dos parámetros:  (que es la pendiente), y  (que es la ordenada al origen).
• La ordenada al origen  indica el valor en el cual la recta interseca al eje  . Es decir que la intersección entre la recta y el eje  es siempre en el punto .
• Dos rectas paralelas tienen la misma pendiente.
• Si el producto entre las pendientes de dos rectas es igual a , entonces las rectas son perpendiculares. Vale también la implicación recíproca (es decir, si dos rectas son perpendiculares el producto de las pendientes es igual a menos uno).
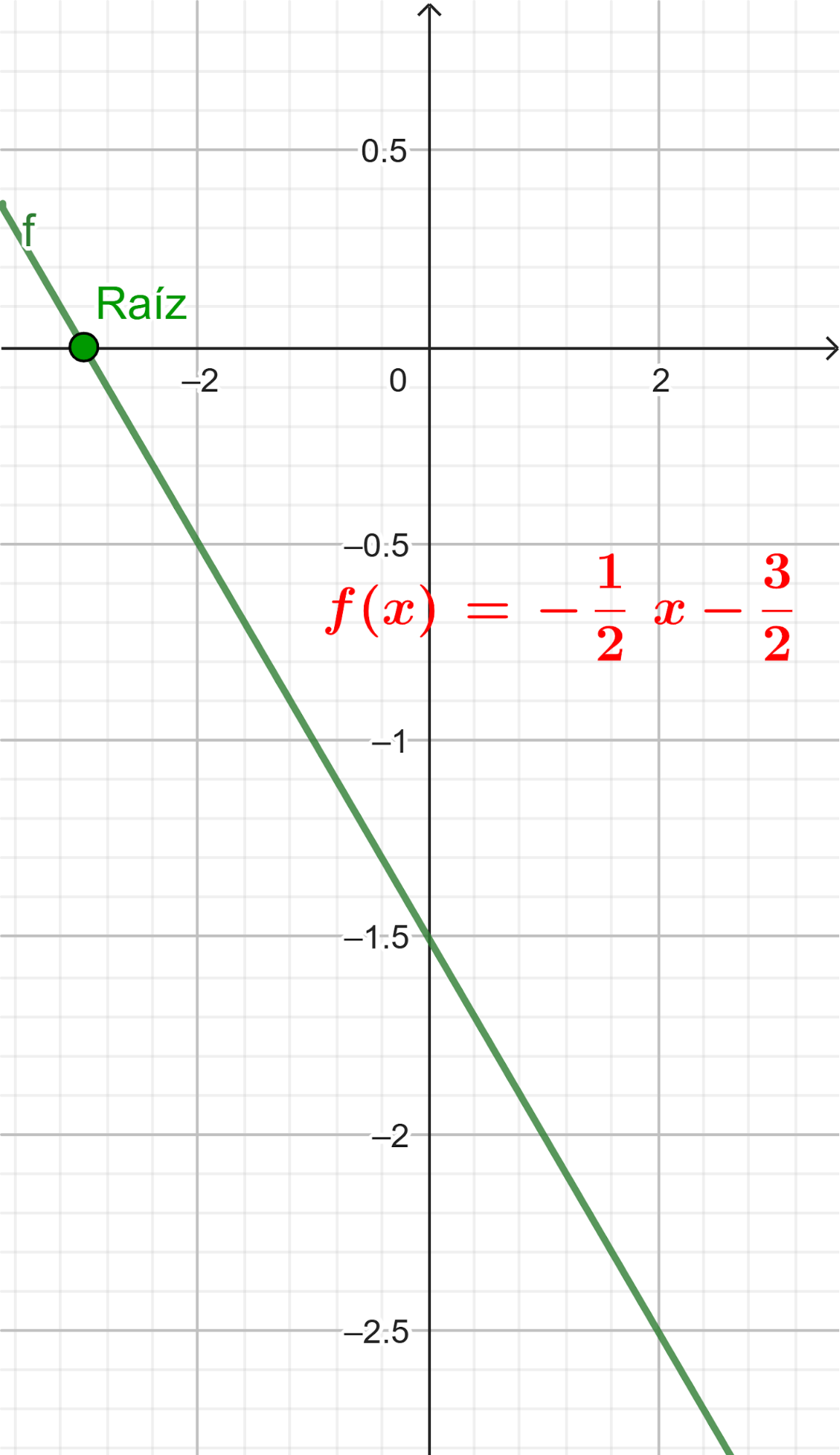
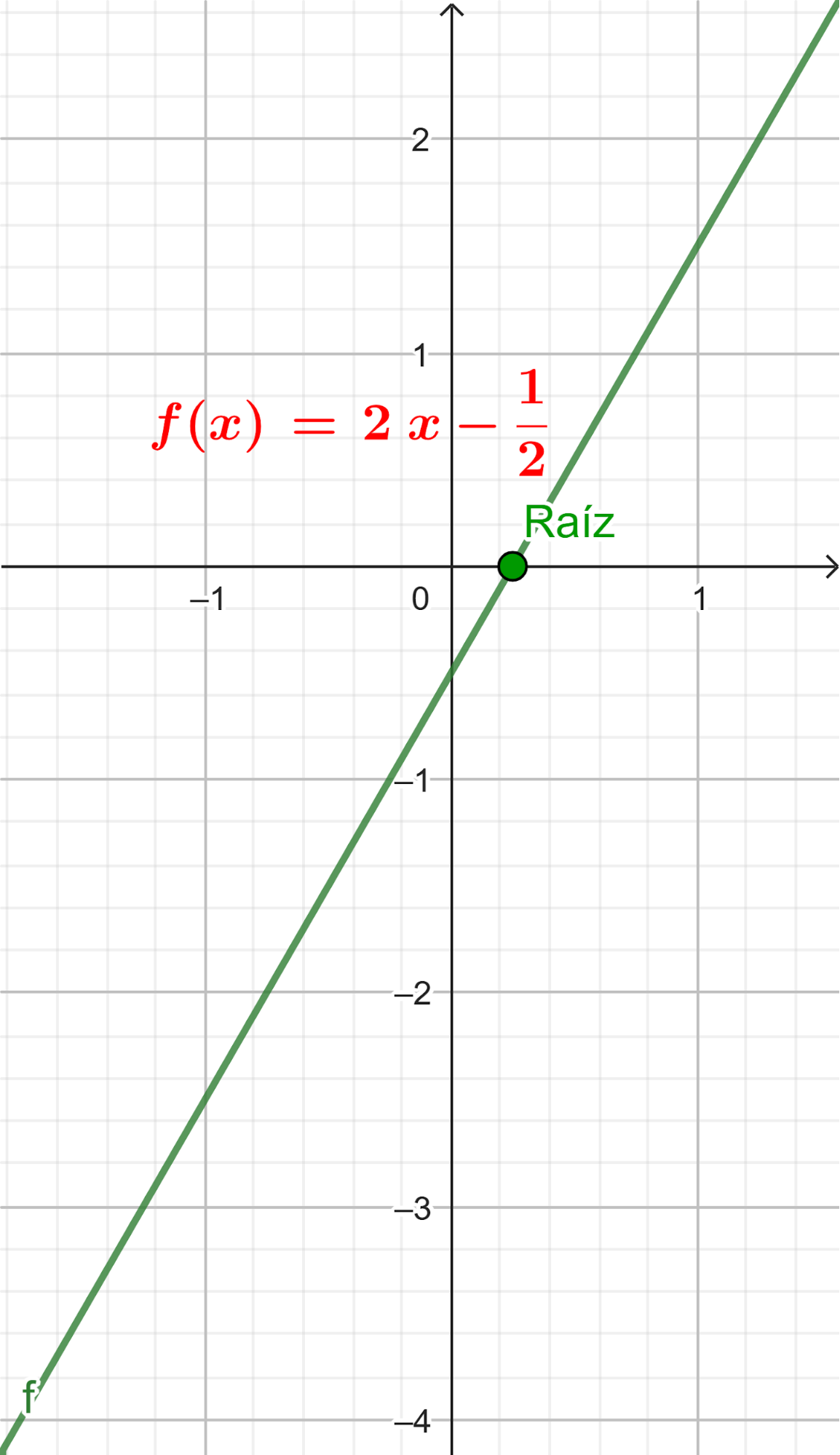
• La raíz de una función es el valor en el cual su gráfica interseca al eje .
• En el caso de una función lineal, la raíz es  siempre que .
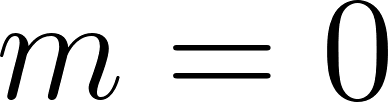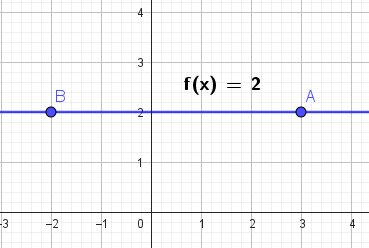
• Si  y  la función no tiene raíz.
• Para el caso particular , la función es constante, coincide con el eje  y tiene infinitas raíces.
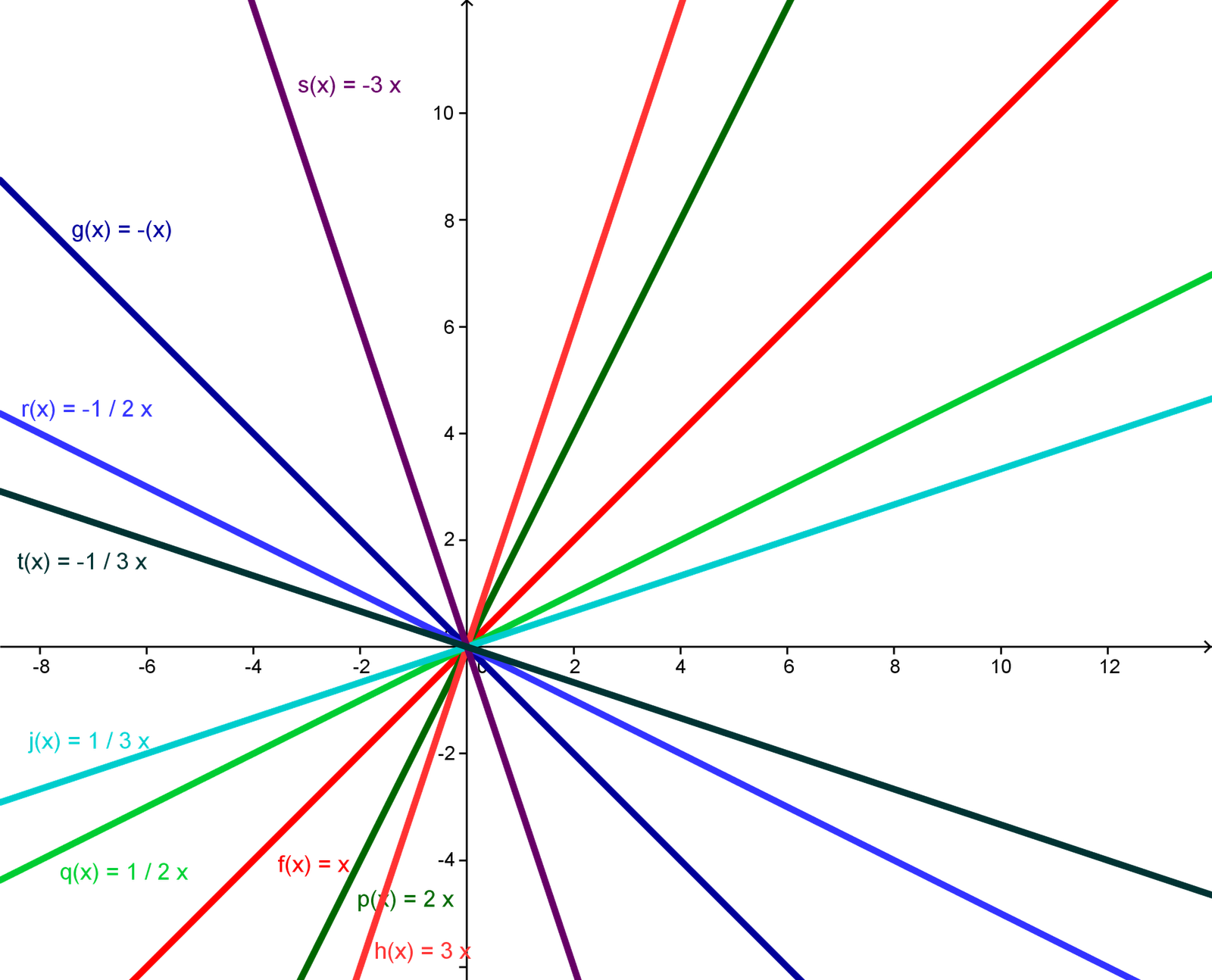
• La pendiente  es igual a la tangente del ángulo que forma la recta con el eje .
• Equivalentemente: . A esta expresión la denominamos cociente incremental.
• Si  entonces la recta es paralela al eje .

Intersección entre dos rectas

        Si dos rectas no son paralelas (es decir, si sus pendientes son diferentes) entonces se intersecan en un punto.

¿Cómo hallamos el punto de intersección de las rectas?

Proponemos un ejemplo.

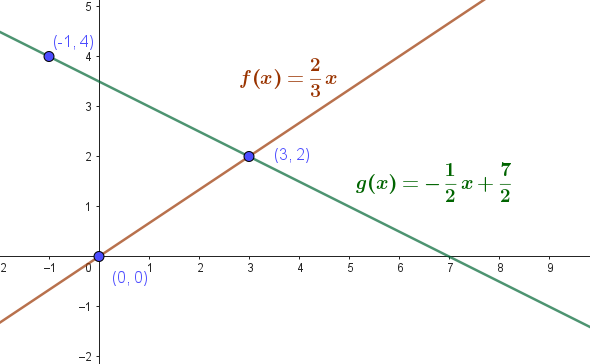
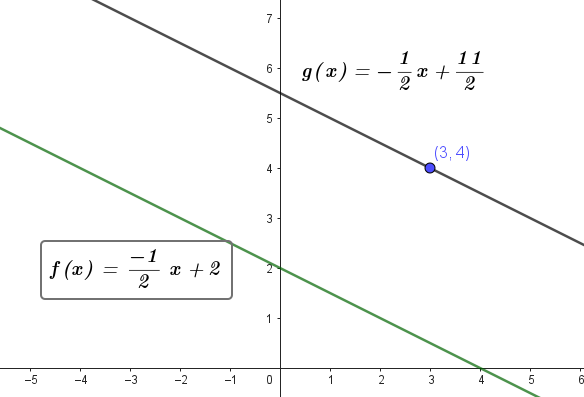
Hallaremos la intersección entre las gráficas de  e , de la siguiente manera:

1. Escribimos el sistema de ecuaciones:
2. Igualamos ambas ecuaciones:
3. Resolvemos la ecuación y obtenemos:
4. Reemplazamos el valor de  obtenido en ambas funciones, para verificar la resolución de la ecuación. Debemos obtener en ambas funciones el mismo valor de .
5. Escribimos el punto de intersección:

Nota: Este procedimiento es válido para encontrar la intersección entre cualquier par de funciones, sean o no funciones lineales.

1. Escribimos el sistema de ecuaciones:

2. Igualamos ambas ecuaciones:

3. Resolvemos la ecuación y obtenemos:

4. Reemplazamos el valor de  obtenido en ambas funciones, para verificar la resolución de la ecuación. Debemos obtener en ambas funciones el mismo valor de .

5. Escribimos el punto de intersección:

Construcción de la ecuación de la recta a partir de algunos datos

Existen distintas variantes para construir la ecuación de una recta a partir de ciertos datos.

En algunos casos contamos con la gráfica de una recta, o con algunos datos acerca de ella (por ejemplo un par de puntos, o un punto y su pendiente) y necesitamos hallar la ecuación de dicha recta, entonces (conociendo el dato de que se trata de una función lineal) planteamos la ecuación  en la cual las incógnitas son  y  y reemplazamos los datos. Problema Halle la ecuación de la recta determinada por los puntos  y .

Resolución. Planteamos la ecuación . Sabemos que, si  vale  entonces  vale . Por lo tanto reemplazamos los valores de  e  en la ecuación y obtenemos:

De la misma manera, obtenemos la ecuación:

Despejamos una de las incógnitas ( o ) en ambas ecuaciones, por ejemplo:

Igualamos y resolvemos:

Reemplazamos el valor de  en ambas ecuaciones y obtenemos .

Luego la ecuación de la recta que buscada es:

Comprobamos que la expresión que hallamos es correcta. Para ello, reemplazamos en la ecuación las coordenadas de los puntos dados. Obtenemos una identidad. Las cuentas quedan a cargo del estudiante. Otra forma de resolver el mismo problema es hallar la pendiente de la recta a partir de los dos puntos dados.

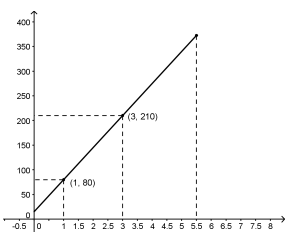
Recordamos que la pendiente de una recta se define como:

entonces planteamos:

Reemplazamos el valor obtenido de  y las coordenadas de alguno de los puntos dados obtenemos:

Despejamos el valor de :

Escribimos la ecuación de la recta buscada:

Podemos verificar que la ecuación obtenida es correcta reemplazando en ella las coordenadas del otro punto dado.

Comentario. En general, la ecuación de la recta con pendiente  que contiene al punto  es:

Si conocemos dos puntos de la recta, podemos hallar  como el cociente incremental .

06: Para Seguir Pensando:

PARA SEGUIR PENSANDO...

• Les proponemos ahora resolver los Problemas 6, 7, 8, 9, 10 y 11. 
• Recuerden que sugerimos resolver estos problemas pero la guía tiene muchos más, por eso Uds. deben resolver todos los problemas para comprender mejor el tema.

Problema 6:

Dado el punto de coordenadas .

1. Escriban las ecuaciones de dos rectas distintas que pasen por este punto. ¿Cómo las hallaron? Escriban un breve texto explicando las estrategias que pusieron en juego para hallar las ecuaciones.
2. ¿Por qué es tan importante esta propiedad? Mencionen al menos dos razones de su importancia.
3. ¿Qué nombre le podríamos poner a la propiedad?

Resolución Problema 6:

1. Dado el punto  planteamos otro punto  para la primer recta y  para la otra recta, y procedemos a calcular sus pendientes y la segunda ordenada al origen, ya que para la primera, al plantear el origen como segundo punto .

Para la recta que pasa por los puntos  y

         Comprobándose lo planteado en el texto

Con lo cuál la primer recta puede ser:

Para la recta que pasa por los puntos  y

Con lo cuál la segunda recta puede ser:

2. Nos permite hallar cualquier recta conociendo al menos un punto, es simple de realizar.
3. Propiedad de la recta.

Problema 7:

Dados los puntos de coordenadas  y .

1. Escriban las ecuaciones de dos rectas distintas que pasen por estos puntos. ¿Cómo las hallaron?
2. Escriban la ecuación de una recta que pase por estos dos puntos a la vez. ¿Cómo la hallaron?

1. Dado dos puntos  y , averiguamos la pendiente  y el origen de ordenada :

Para la recta que pasa por los puntos  y

Con lo cuál la primer recta puede ser:

Problema 8:

        Hallen la expresión de la función lineal  tal que la recta correspondiente cumpla que:

1. Su pendiente es  y contiene al punto .
2. Su pendiente es  y contiene al punto .
3. Contiene los puntos  y .
4. Contiene los puntos  y .
5. Contiene los puntos  y .
6. Contiene los puntos  y .
7. Contiene al punto .

Resolución Problema 8:

1. Siendo su pendiente  y el punto  

Con lo cuál la función lineal es:

2. Siendo su pendiente  y el punto

Con lo cuál la función lineal es:

3. Conteniendo los puntos  y hallamos su pendiente y origen de ordenada.

Con lo cuál la función lineal es:

4. Conteniendo los puntos  y hallamos su pendiente y origen de ordenada..

Con lo cuál la función lineal es:

5. Conteniendo los puntos  y hallamos su pendiente y origen de ordenada..

Con lo cuál la función lineal es:

6. Conteniendo los puntos  y hallamos su pendiente y origen de ordenada..

No existe pendiente No se puede armar una recta que pase por esos 2 puntos, ya que comparte el mismo x, generando una línea vertical que por definición no es una función lineal.

7. Conteniendo al punto  planteamos otro punto por ejemplo el origen y hallamos su pendiente.

Con lo cuál la función lineal es:

Problema 9: 

Obtengan la ecuación de la recta y representen en cada uno de los siguientes casos:

1. Es paralela a  y pasa por .
2. Es perpendicular a  y pasa por .
3. Pasa por  y por .
4. Interseca al eje  en  y tiene pendiente .
5. Interseca al eje  en   y tiene pendiente .
6. Es horizontal y pasa por .
7. Tiene raíz igual a  y ordenada al origen .
8. Corta al eje  en  y pasa por .

Resolución Problema 9:

1. Teniendo en cuenta que una recta es paralela a sí misma, podemos usar la dada en el problema y verificar que pase por el punto:

 con lo cual el punto  no se encuentra en la recta y deberemos buscar una que sí cumpla lo solicitado.

Entonces, por la teoría sabemos que la pendiente debe ser la misma, así que planteamos la misma pendiente y el punto de paso y averiguamos la ordenada al origen:

Por lo tanto la recta paralela que pasa por el punto  es:

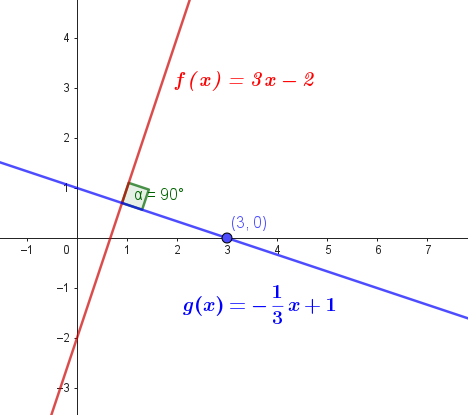
2. Es perpendicular a  y pasa por .

De la teoría:

        “Si el producto entre las pendientes de dos rectas es igual a , entonces las rectas son perpendiculares. Vale también la implicación recíproca (es decir, si dos rectas son perpendiculares el producto de las pendientes es igual a menos uno).”

Entonces:

         Despejamos

Y debe pasar por

Quedando:

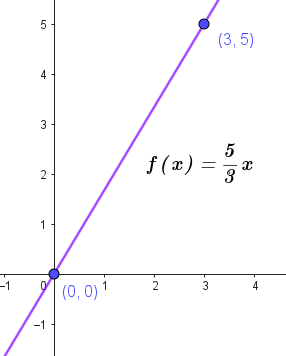
3. Pasa por  y por . Hallamos la pendiente y como uno de los puntos es el origen, tomamos su coordenada  como origen de ordenada.

Por lo tanto, la recta es:

4. Interseca al eje  en  y tiene pendiente . Tenemos todos los datos, su pendiente y origen de ordenada por lo cual, la recta es:

5. Interseca al eje  en   y tiene pendiente . Nos da su raíz y la pendiente, al ser su raíz el punto es  por lo tanto nos queda averiguar la ordenada al origen.

De la teoría tenemos:

        “En el caso de una función lineal, la raíz es  siempre que .”

Entonces:

Quedando la recta:

6. Es horizontal y pasa por . Al ser horizontal es:

7. Tiene raíz igual a  y ordenada al origen . Averiguamos la pendiente.

Quedando la recta:

8. Corta al eje  en  y pasa por . Tenemos el origen de ordenada  y un punto de paso, averiguamos su pendiente.

Con lo cual la recta es:

Problema 10:

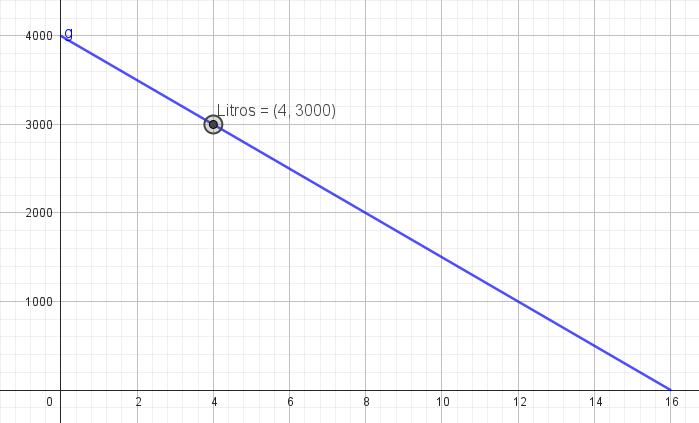
El siguiente gráfico representa la distancia de un auto a Buenos Aires en función del tiempo.

1. Armen una tabla de valores que representan distintos momentos del viaje y márquenlos en el gráfico:

1. El momento en que parte.
2. Cuando pasaron 2 horas y media de viaje.
3. Cuando se encuentra a 300 km de Buenos Aires.
4. Cuando pasaron 4 horas de viaje
5. Cuando se encuentra a 230 km de Buenos Aires.
6. El momento en que finaliza el viaje. ¿Llega a Mar del Plata?

2.  Definan una función (armen una fórmula que establezca una relación entre  e  y expresen un dominio) de manera tal que el gráfico anterior representa dicha función.

Resolución Problema 10:

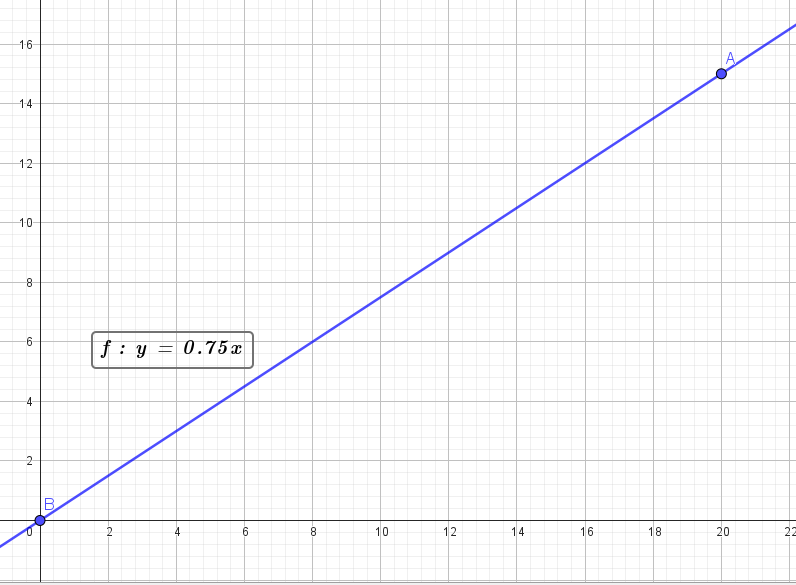
1. Teniendo en cuenta el gráfico que nos muestra dos puntos de la recta podemos armarla averiguando su pendiente y el origen de ordenada.

Ahora la ordenada al origen:

Nos queda la función:

1. El auto parte en x=0 a 15 km de Buenos Aires
2. A las dos horas y media se encontraba a:

3. Se encuentra a 300 km de Buenos Aires en:

4. Cuando pasaron cuatro horas se encontraba a:

5. Se encuentra a 230 km de Buenos Aires en:

6. El momento en que finaliza el viaje. ¿Llega a Mar del Plata? Finaliza en :

 Aún no llegó a Mar del Plata, ya que se encuentra a 415 km de Buenos Aires.

 Necesita seis horas y cuarto aproximadamente para llegar a Buenos Aires.

        Con las respuestas ya podemos realizar la tabla:

2. La función es:

         Su

Problema 11:

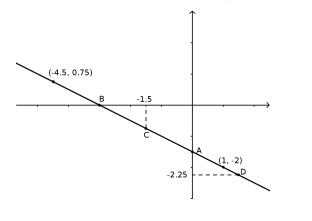
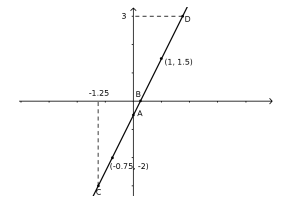
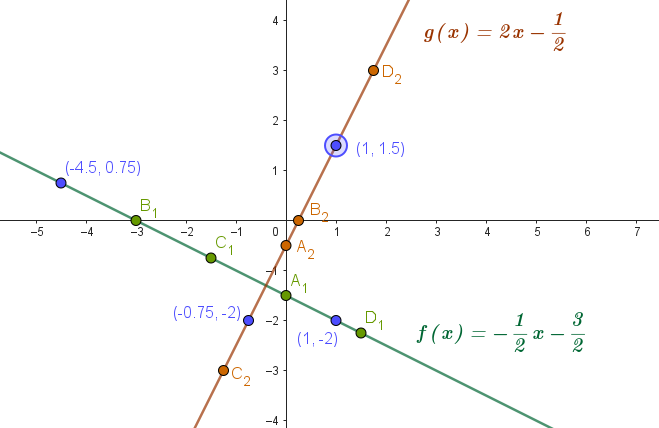
        Los siguientes gráficos representan funciones lineales.

1. Armen la fórmula de cada función.
2. Den las coordenadas de los puntos A, B, C y D.

Resolución Problema 11:

1. Del gráfico 1 podemos observar dos puntos  y .

Del gráfico 2 podemos observar dos puntos  y .

Por lo tanto tenemos datos suficientes para hallar pendientes y ordenadas al origen de ambos gráficos.

Gráfico 1:

         es

La función es:

Gráfico 2:

         es

La función es:

2. Den las coordenadas de los puntos A, B, C y D.

Gráfico 1:

Gráfico 2:

Práctica

Problema 1 Un auto sale de una ciudad que está sobre la Ruta Nacional 2, entre Buenos Aires y Mar del Plata. En la siguiente tabla se informa sobre la distancia a la que se encuentra de Buenos Aires en distintos momentos de su viaje. Se supone que el auto viaja siempre a la misma velocidad.

1. ¿Es cierto que a las tres horas de salir está a 320 km de Buenos Aires?.
2. ¿A qué distancia de Buenos Aires estará a las tres horas y media de haber salido?.
3. ¿A qué distancia de Buenos Aires se encuentra la ciudad de donde partió?.
4. Realicen un gráfico que represente la distancia del auto a Buenos Aires a medida que transcurre el tiempo de viaje. Agreguen al gráfico cartelitos con anotaciones para explicar la información importante que se puede observar en distintas partes.
5. ¿A qué velocidad viaja el auto?.
6. Propongan una fórmula que permita calcular la distancia del auto a Buenos Aires en función del tiempo transcurrido.

Problema 2 Volviendo al Problema 1 respondan:

1. Otro auto parte desde otra ciudad que está en la ruta entre Buenos Aires y Mar del Plata, ubicada a 10 km de Buenos Aires. Este auto también viaja siempre a la misma velocidad: 120 km/h. ¿Se van a cruzar estos dos vehículos? En caso afirmativo, ¿en dónde y en qué momento?.
2. Si este último auto hubiese partido a una velocidad de 95 km/h, ¿se habría cruzado con el primero? En caso afirmativo, ¿en dónde y en qué momento?.
3. Realicen, en un mismo sistema de ejes, tres gráficos de manera que cada uno represente la distancia de cada uno de los autos a Buenos Aires en función del tiempo.

Problema 3 Roberto está por hacer un viaje y está averiguando para alquilar un auto. Averiguó en dos compañías:

• La compañía A le cobra $800 fijos y $1,10 por kilómetro recorrido.
• La compañía B le cobra $150 fijos y $1,35 por cada kilómetro recorrido.

1. Si estima que va a recorrer 1000 Km, ¿qué compañía le conviene contratar? ¿Y si recorriera 5000 Km?.
2. Armen una fórmula correspondiente a la compañía A y otra correspondiente a la compañía B, que represente el costo del alquiler en función de los kilómetros recorridos. ¿A partir de qué kilometraje le conviene cada compañía?.
3. ¿Cuáles de estos gráficos sirven para representar la situación?:

4. Si finalmente Roberto eligió la compañía A y cuando terminó el viaje el costo del alquiler fue de $3355,30, ¿cuántos kilómetros recorrió?

Problema 4:

        El gráfico representa el proceso de vaciado de un tanque de agua.

1.  ¿Qué cantidad de agua tenía el tanque cuando empezó a vaciarse?.
2. ¿Cuánto tardó en vaciarse?.
3. ¿Cuántos litros por minuto salían del tanque mientras se vaciaba?.
4. Marquen sobre el gráfico el punto que representa el momento en que el tanque tenía 3000 litros. ¿Cuánto tiempo había transcurrido desde que comenzó a vaciarse?.
5. Escriban una fórmula que calcule la cantidad de agua que había en el tanque a los  minutos de haber comenzado a vaciarse.

Problema 5:

        El gráfico representa el proceso de llenado de un tanque de agua a partir del momento en que se abrió una canilla.

1. ¿Qué cantidad de agua tenía el tanque cuando se abrió la canilla y empezó a llenarse?.
2. ¿Cuántos litros por minuto entraron al tanque mientras se llenaba?.
3. Marquen sobre el gráfico el punto que representa el momento en que el tanque tenía 1500 litros. ¿Cuánto tiempo había transcurrido desde que comenzó a llenarse?.
4. Escriban una fórmula que calcule la cantidad de agua que había en el tanque a los  minutos de haber comenzado a llenarse.

Problema 6:

Dado el punto de coordenadas .

1. Escriban las ecuaciones de dos rectas distintas que pasen por este punto. ¿Cómo las hallaron? Escriban un breve texto explicando las estrategias que pusieron en juego para hallar las ecuaciones.
2. ¿Por qué es tan importante esta propiedad? Mencionen al menos dos razones de su importancia.
3. ¿Qué nombre le podríamos poner a la propiedad?

Problema 7:

Dados los puntos de coordenadas  y .

1. Escriban las ecuaciones de dos rectas distintas que pasen por estos puntos. ¿Cómo las hallaron?.
2. Escriban la ecuación de una recta que pase por estos dos puntos a la vez. ¿Cómo la hallaron?.

Problema 8:

        Hallen la expresión de la función lineal  tal que la recta correspondiente cumpla que:

1. Su pendiente es  y contiene al punto .
2. Su pendiente es  y contiene al punto .
3. Contiene los puntos  y .
4. Contiene los puntos  y .
5. Contiene los puntos  y .
6. Contiene los puntos  y .
7. Contiene al punto .

Problema 9: 

Obtengan la ecuación de la recta y representen en cada uno de los siguientes casos:

1. Es paralela a  y pasa por .
2. Es perpendicular a  y pasa por .
3. Pasa por  y por .
4. Interseca al eje  en  y tiene pendiente .
5. Interseca al eje  en   y tiene pendiente .
6. Es horizontal y pasa por .
7. Tiene raíz igual a  y ordenada al origen .
8. Corta al eje  en  y pasa por .

Problema 10:

El siguiente gráfico representa la distancia de un auto a Buenos Aires en función del tiempo.

1. Armen una tabla de valores que representan distintos momentos del viaje y márquenlos en el gráfico:

1. El momento en que parte.
2. Cuando pasaron 2 horas y media de viaje.
3. Cuando se encuentra a 300 km de Buenos Aires.
4. Cuando pasaron 4 horas de viaje
5. Cuando se encuentra a 230 km de Buenos Aires.
6. El momento en que finaliza el viaje. ¿Llega a Mar del Plata?.

2. Definan una función (armen una fórmula que establezca una relación entre  e  y expresen un dominio) de manera tal que el gráfico anterior representa dicha función.

Problema 11:

        Los siguientes gráficos representan funciones lineales.

1. Armen la fórmula de cada función.
2. Den las coordenadas de los puntos A, B, C y D.

Problema 12 Escriban la fórmula de una función que a cada longitud expresada en centímetros la devuelva expresada en pulgadas (¿Qué información necesitan averiguar?).

Problema 13 Escriban la fórmula de una función que a cada temperatura expresada en centígrados la devuelva expresada en grados Fahrenheit (¿Qué información necesitan averiguar?).

Problema 14 Daniel y Anders estaban en el laboratorio y tuvieron un diálogo:

• –Oye, Anders —preguntó Daniel—, ¿podrías decirme a qué temperatura está esa muestra de nitrógeno?
• Anders consultó un termómetro y su respuesta fue simplemente un número. Daniels insistió:
• —Necesito que me aclares si tu respuesta es en grados Celsius o en grados Fahrenheit.
• —No—advirtió Anders— no hace falta aclararlo. ¿A qué temperatura estaba la muestra de nitrógeno?.

Problema 15 Metros (m), pies (ft) y yardas (yd) son distintas unidades de longitud. La tabla 2.1 describe la equivalencia entre metros y pies. La tabla 2.2 describe la equivalencia entre pies y yardas.

Tabla 2.1: metros-pies

Tabla 2.2: pies-yardas

1. Encuentren una función que transforme longitudes expresadas en metros a yardas y escriban su fórmula.
2. Escriban la fórmula de una función que transforma yardas en pulgadas. ¿Qué información no incluida en el enunciado de este problema necesitarán?.
3. Anders dice que la Tabla 2.1 está mal hecha porque si grafica los puntos estos no quedan estrictamente alineados. Sin embargo, la tabla está tomada de una página seria de Internet. ¿Tiene razón Anders? ¿Es confiable la tabla? Esto es una discusión. Escriban una opinión con algún argumento que permita defenderla.

Problema 16 Para la función lineal , se pide:

1. Indiquen dos puntos de la gráfica de .
2. Indiquen dos puntos que no pertenezcan a su gráfica.
3. Hallen los puntos donde la gráfica corta a cada uno de los ejes coordenados.
4. ¿Qué relación pueden establecer entre los coeficientes de  y las coordenadas de esos puntos?.

La abreviatura “ft” para pies viene del Inglés: feet=pies.

Problema 17 Decidan, en cada caso, si los pares de rectas correspondientes a las siguientes funciones lineales, son o no paralelas. En caso de no serlo, hallen las coordenadas del punto de intersección. Interpreten la solución hallada en un gráfico.

1.  y .
2.  y .
3.  y .
4.  y .
5.  y .

Problema 18 Para una fiesta que está planeando, Joaquín quiere comprar 20 botellas de Gorgorito. Tiene 13 envases guardados de otros eventos. El supermercado chino de la vuelta le cobra  la botella de Gorgorito y  adicionales si no trae envase. El supermercado que está a dos cuadras le cobra  la botella de Gorgorito y  adicionales por envase.

1.  ¿En qué supermercado le conviene comprar?
2. Si le pidió a los amigos que trajeran envases vacíos y piensa que esta iniciativa le reportará unos 4 envases más ¿En qué supermercado le conviene comprar?.
3. La fiesta parece que será un éxito, ya que recibió más confirmaciones por Facebook de las que pensaba y cree que las 20 botellas no alcanzarán. Si supone que necesitará 32 botellas, ¿a qué súper le conviene ir a comprarlas?.
4. ¿Qué estrategia le conviene implementar para minimizar costos?.
5. Si estima que se van a consumir  botellas y los amigos van a contribuir con  envases, ¿Qué estrategia le conviene implementar para cada ?.

Problema 19()(Problema de modelización)

Tres compañías de telefonía celular estudian cómo ofrecer su

plan para el nuevo Mobicón Esmarfón, con las prestaciones

que se ven en el recuadro.

• La compañía 1: Regala el teléfono y cobra un abono de  por mes.
• La compañía 2: Cobra el teléfono  y un abono mensual de
• La compañía 3: Cobra el teléfono  da tres meses de abono gratuito y a partir del cuarto mes cobra el abono .

1. Construyan un modelo con GeoGebra, en el que A1, A2, A3, C2 y C3, sean deslizadores. Investiguen los precios del mercado para elegir en qué rangos razonables se pueden mover esos deslizadores. El modelo debe servir para describir el costo que tiene para un cliente elegir cada una de las tres compañías, en función del tiempo que usará el teléfono
2. Jueguen con el modelo y elijan distintos valores de los deslizadores para que a un cliente que elegirá una compañía durante seis meses, un año, dos años, etc. le convenga la compañía 1, la 2 o la 3. Escriban en cada caso una explicación de por qué le convendrá una u otra.